1 INTRODUCTION

Ultracold ions in traps have remained the subject of active research in the field of quantum computing for many years. This platform has a number of basic advantages over alternative ones. They include a long coherence time [1]; a strong Coulomb interaction, which makes it possible to effectively entangle the states of qubits [2]; and a high degree of isolation of the system from external disturbances. In addition, interest in the ion platform is further stimulated by progress in the creation of traps with low heating rates [3], high optical access [4], and the possibility of changing the configuration of the ion chain [5].

One of the most important tasks for the implementation of trapped-ion based quantum computing is the control of the ion temperature. In order to ensure high fidelity of quantum operations (especially those involving entanglement), the ion chain usually has to be cooled as close to the ground vibrational state as possible [6, 7]. Despite the progress attained in the development of algorithms that are less demanding on the temperature of the chain [8, 9], the impact of this parameter on the fidelity of operations remains significant.

Currently available methods for measuring the ion temperature and/or heating rate include the measurements of the ion fluorescence signal in the course of its Doppler cooling [10, 11], the spectroscopy of side vibrational frequencies [12], and methods based on coherent effects like induced transparency [13]. Together they make it possible to determine the ion temperature in a fairly broad range. However, the first method is applicable only for very large values of the average vibrational quantum number (104–105), while the second, on the contrary, gives sufficiently accurate results only at low temperatures and is typically used after deep cooling, when only a few vibrational levels are occupied on average. The third method works satisfactorily in the intermediate range, but is quite technically sophisticated because at least two mutually coherent sources of optical radiation with different frequencies are required in this case.

Here, we propose a method for measuring the temperature of the ion chain based on the dephasing of resonant Rabi oscillations at the carrier frequency of a narrow optical transition in the ions under study. This method is less demanding on the experimental setup, since it requires no laser sources in addition to those used to control the optical qubit. We present an analytical formula describing the time dependence of the population of the upper ion state and generalizing the theory set out in [14] to the case of an arbitrary number of ions. We then demonstrate the applicability of this formula in actual experiments to estimate the heating rate of a single ion in a trap and to determine the temperature of a chain of five ions.

2 DEPHASING OF RABI OSCILLATIONS

Consider the one-dimensional motion of a chain of N ions along some axis of the trap. In total, there are N normal vibrational modes of the chain, characterized by N secular frequencies \({{\omega }_{k}}\) (\(1 \leqslant k \leqslant N\)). Each of these modes represents an independent oscillator with a frequency \({{\omega }_{k}}\), so that the quantum state of an individual ion is represented by the vector

$${\text{|}}\psi \rangle = {\text{|el}}\rangle {\text{|}}{{n}_{1}},{{n}_{2}}, \ldots ,{{n}_{N}}\rangle = {\text{|el}}\rangle {\text{|}}\{ {{n}_{k}}\} \rangle ,$$
(1)

where \({\text{|el}}\rangle \in \left\{ {{\text{|}}0\rangle ,|1\rangle } \right\}\) stands for the electron state of the ion and \({{n}_{k}}\) is the number of phonons in the kth vibrational mode. When radiation that propagates along the axis under consideration and is resonant with the \({\text{|}}0\rangle \leftrightarrow {\text{|}}1\rangle \) electron transition acts on an ion in the chain, Rabi oscillations between states with the same sets of \(\{ {{n}_{k}}\} \) occur with the angular frequency

$${{\Omega }_{{\{ {{n}_{k}}\} }}} = {{\Omega }_{0}}\left| {\left\langle {\{ {{n}_{k}}\} \left| {\exp \left( {i\sum\limits_{k = 1}^N {{\eta }_{k}}({{{\hat {a}}}_{k}} + \hat {a}_{k}^{\dag })} \right)} \right|\{ {{n}_{k}}\} } \right\rangle } \right|,$$
(2)

where \({{\Omega }_{0}}\) is the Rabi frequency of the ion at rest, \({{\hat {a}}_{k}}\) and \(\hat {a}_{k}^{\dag }\) are the ladder operators for the kth phonon mode, and \({{\eta }_{k}}\) is the Lamb–Dicke parameter for the given ion in the kth mode. Using the commutativity of the ladder operators of different modes, we can represent this expression in a more convenient form

$${{\Omega }_{{\{ {{n}_{k}}\} }}} = {{\Omega }_{0}}\left| {\prod\limits_{k = 1}^N \langle {{n}_{k}}{\text{|}}{{e}^{{i{{\eta }_{k}}({{{\hat {a}}}_{k}} + \hat {a}_{k}^{\dag })}}}{\text{|}}{{n}_{k}}\rangle } \right|.$$
(3)

This is the product of Debye–Waller-like factors [15]

$$\left| {\langle {{n}_{k}}{\text{|}}{{e}^{{i{{\eta }_{k}}({{{\hat {a}}}_{k}} + \hat {a}_{k}^{\dag })}}}{\text{|}}{{n}_{k}}\rangle } \right| = {{e}^{{ - \eta _{k}^{2}/2}}}\left| {{{L}_{{{{n}_{k}}}}}(\eta _{k}^{2})} \right|,$$
(4)

where \({{L}_{n}}(x)\) is the \(n\)th Laguerre polynomial. As far as the Lamb–Dicke regime, which implies that \(\sqrt {{{{\overline n }}_{k}}} {\kern 1pt} {{\eta }_{k}} \ll 1\), usually holds for ions cooled to the Doppler limit, all but the lowest power of \({{\eta }_{k}}\) can be omitted in the Laguerre polynomial in this expression, so that

$$\begin{gathered} \left| {\langle {{n}_{k}}{\text{|}}{{e}^{{i{{\eta }_{k}}({{{\hat {a}}}_{k}} + \hat {a}_{k}^{\dag })}}}{\text{|}}{{n}_{k}}\rangle } \right| \approx {{e}^{{ - \eta _{k}^{2}/2}}}(1 - {{n}_{k}}\eta _{k}^{2}) \\ \approx 1 - ({{n}_{k}} + 1{\text{/}}2)\eta _{k}^{2}. \\ \end{gathered} $$
(5)

Then, to the accuracy of order \(\eta _{k}^{2}\), the Rabi frequency can be written as

$$\begin{gathered} {{\Omega }_{{\{ {{n}_{k}}\} }}} \approx {{\Omega }_{0}}\prod\limits_{k = 1}^N \left( {1 - ({{n}_{k}} + 1{\text{/}}2)\eta _{k}^{2}} \right) \\ \approx {{\Omega }_{0}}\left( {1 - \sum\limits_{k = 1}^N ({{n}_{k}} + 1{\text{/}}2)\eta _{k}^{2}} \right). \\ \end{gathered} $$
(6)

If the initial population of state \({\text{|}}0\rangle {\text{|}}\{ {{n}_{k}}\} \rangle \) is \({{p}_{{\{ {{n}_{k}}\} }}}\), the population of state \({\text{|}}1\rangle {\text{|}}\{ {{n}_{k}}\} \rangle \) varying with time under the effect of resonant radiation equals

$${{P}_{{\{ {{n}_{k}}\} }}}(t) = \frac{{{{p}_{{\{ {{n}_{k}}\} }}}}}{2}\left( {1 - \cos ({{\Omega }_{{\{ {{n}_{k}}\} }}}t)} \right).$$
(7)

The total population of state \({\text{|}}1\rangle \) is obtained as the sum of terms represented by Eq. (7) over all possible sets of \(\{ {{n}_{k}}\} \):

$$P(t) = \frac{1}{2}\sum\limits_{\{ {{n}_{k}}\} } {{p}_{{\{ {{n}_{k}}\} }}}\left( {1 - \cos ({{\Omega }_{{\{ {{n}_{k}}\} }}}t)} \right).$$
(8)

If the Rabi frequency were independent of the vibrational quantum numbers \({{n}_{k}}\), all oscillations in the above sum would be in phase, and the dependence \(P(t)\) would be a pure sinusoid with constant amplitude and frequency. However, according to Eq. (6), a weak dependence of the Rabi frequency on \(\{ {{n}_{k}}\} \) exists. Then, oscillations corresponding to different \(\{ {{n}_{k}}\} \) fall out of phase after some time (this is similar to the effect of wave packet spreading with time), and the visibility of oscillations decreases (see Fig. 1).

Fig. 1.
figure 1

Illustration of the dephasing of Rabi oscillations. Gray lines show oscillations of the population for the first ten modes and black line is the weighted sum over all modes.

Full size image

The depths of typical ion traps are much larger than the average thermal energy of the ions even in the absence of cooling. Thus, the sum over \(\{ {{n}_{k}}\} \) can be replaced by an infinite series:

$$P(t) = \frac{1}{2}\sum\limits_{{{n}_{1}} = 0}^\infty \cdots \sum\limits_{{{n}_{N}} = 0}^\infty {{p}_{{\{ {{n}_{k}}\} }}}\left( {1 - \cos ({{\Omega }_{{\{ {{n}_{k}}\} }}}t)} \right).$$
(9)

If

$$\sum\limits_{{{n}_{1}} = 0}^\infty \cdots \sum\limits_{{{n}_{N}} = 0}^\infty {{p}_{{\{ {{n}_{k}}\} }}} = a,$$
(10)

i.e., the initial population of level \({\text{|}}0\rangle \) equals a, then, taking into account the thermal distribution with average phonon-mode populations \({{\bar {n}}_{k}}\), we have

$${{p}_{{\{ {{n}_{k}}\} }}} = a{\kern 1pt} \frac{{\exp \left( { - \sum\limits_{k = 1}^N {{\alpha }_{k}}{{n}_{k}}} \right)}}{{\prod\limits_{k = 1}^N ({{{\bar {n}}}_{k}} + 1)}},$$
(11)

where \({{e}^{{ - {{\alpha }_{k}}}}} = {{\bar {n}}_{k}}{\text{/}}({{\bar {n}}_{k}} + 1)\). Substituting Eqs. (6) and (11) into Eq. (9) and expressing the cosine as the sum of two exponentials, we obtain

$$P(t) = \frac{a}{2} - \frac{a}{{4\prod\limits_{k = 1}^N ({{{\bar {n}}}_{k}} + 1)}}$$
$$ \times \;\sum\limits_{{{n}_{1}} = 0}^\infty \cdots \sum\limits_{{{n}_{N}} = 0}^\infty \left[ {{{e}^{{i{{\Omega }_{0}}t}}}\exp \left( { - \sum\limits_{k = 1}^N ({{\alpha }_{k}}{{n}_{k}}} \right.} \right.$$
(12)
$$ + \;i{{\Omega }_{0}}\eta _{k}^{2}t{{n}_{k}} + \left. {\left. {i{{\Omega }_{0}}\eta _{k}^{2}t{\text{/}}{{{2)}}_{{\begin{subarray}{l} {\kern 1pt} \\ {\kern 1pt} \end{subarray}} }}} \right) + {\text{c}}{\text{.c}}{\text{.}}} \right].$$

The term

$$\sum\limits_{{{n}_{1}} = 0}^\infty \cdots \sum\limits_{{{n}_{N}} = 0}^\infty \exp \left( { - \sum\limits_{k = 1}^N {({{\alpha }_{k}}{{n}_{k}} + i{{\Omega }_{0}}\eta _{k}^{2}t({{n}_{k}} + 1{\text{/}}2))} } \right)$$
(13)

can be written as the product of N sums over the values of \({{n}_{k}}\) for each mode of the form

$$\prod\limits_{k = 1}^N \left[ {{{e}^{{ - i{{\Omega }_{0}}\eta _{k}^{2}t/2}}}\sum\limits_{{{n}_{k}} = 0}^\infty \exp ( - ({{\alpha }_{k}} + i{{\Omega }_{0}}\eta _{k}^{2}t){{n}_{k}})} \right].$$
(14)

Each of the individual sums can be evaluated as the sum of a geometric progression:

$$\begin{gathered} \sum\limits_{{{n}_{k}} = 0}^\infty \exp ( - ({{\alpha }_{k}} + i{{\Omega }_{0}}\eta _{k}^{2}t){{n}_{k}}) = \frac{1}{{1 - {{e}^{{ - {{\alpha }_{k}} - i{{\Omega }_{0}}\eta _{k}^{2}t}}}}} \\ = \frac{{1 - {{e}^{{ - {{\alpha }_{k}} + i{{\Omega }_{0}}\eta _{k}^{2}t}}}}}{{1 - 2{{e}^{{ - {{\alpha }_{k}}}}}\cos ({{\Omega }_{0}}\eta _{k}^{2}t) + {{e}^{{ - 2{{\alpha }_{k}}}}}}}. \\ \end{gathered} $$
(15)

To characterize the chain as a whole, it is convenient to introduce the parameters \({{r}_{k}} = {{\omega }_{k}}{\text{/}}{{\omega }_{1}}\), where \({{\omega }_{1}}\) is the frequency of the center-of-mass vibrational mode (the mode in which the entire ion chain moves as a whole). The above treatment is valid for any set of \(\left\{ {{{{\bar {n}}}_{k}}} \right\}\) provided that the chain is in the Lamb–Dicke regime. However, the most practically interesting case is the one corresponding to the state after the Doppler cooling of the chain, i.e., the state where the temperatures of all modes are equal. In this situation, the average vibrational quantum numbers of all modes can be expressed in terms of the average number \(\bar {n}\) of phonons in the center-of-mass mode, so that \({{\bar {n}}_{k}} = \bar {n}{\text{/}}{{r}_{k}}\). Then, taking into account the definition of \({{\alpha }_{k}}\), the function \(P(t)\) assumes the form

$$P(t) = \frac{a}{2}\left[ {1 - \frac{{{\text{Re}}\left[ {{{e}^{{i{{\Omega }_{0}}t}}}\prod\limits_{k = 1}^N {{e}^{{ - i{{\Omega }_{0}}\eta _{k}^{2}t/2}}}\left( {1 - \frac{{(\bar {n}{\text{/}}{{r}_{k}}){{e}^{{i{{\Omega }_{0}}\eta _{k}^{2}t}}}}}{{\bar {n}{\text{/}}{{r}_{k}} + 1}}} \right)} \right]}}{{\prod\limits_{k = 1}^N \left( {(\bar {n}{\text{/}}{{r}_{k}} + 1) - 2(\bar {n}{\text{/}}{{r}_{k}})\cos ({{\Omega }_{0}}\eta _{k}^{2}t) + \frac{{{{{(\bar {n}{\text{/}}{{r}_{k}})}}^{2}}}}{{(\bar {n}{\text{/}}{{r}_{k}}) + 1}}} \right)}}} \right]$$
(16)

and depends on the three parameters \(\bar {n}\), a, and \({{\Omega }_{0}}\). The coefficients \({{\eta }_{k}}\) and \({{r}_{k}}\) are determined by the geometry of the trap [16], and the ion vibrational frequencies and can be measured independently with a high accuracy. We note that, in the general case where the vibrations of the chain are excited along all three axes, Eq. (16) is still valid. The only difference will be that, instead of the parameters \({{\eta }_{k}}\), \(\bar {n}\), and \({{r}_{k}}\), the products over the vibrational modes then contain parameters of the type \({{\eta }_{{ik}}}\), \({{\bar {n}}_{i}}\), and \({{r}_{{ik}}}\) (where \(i = x\), y, or z is the axis index), and the Lamb–Dicke coefficients depend on the direction of the beam.

3 MEASUREMENT SETUP

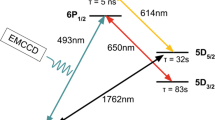
The dephasing of Rabi oscillations was studied for ytterbium ions \(^{{171}}{\text{Y}}{{{\text{b}}}^{ + }}\), whose energy level diagram is shown in Fig. 2. The \(^{2}{{S}_{{1/2}}} \to {{\;}^{2}}{\kern 1pt} {{P}_{{1/2}}}\) transition serves to cool the ion and prepare the state. For this purpose, the main laser beam with a wavelength of 369 nm is split using electro-optical modulators into three frequency components, with two of them being responsible for cooling and the third for pumping the ion into the ground state \(^{2}{{S}_{{1/2}}}(F = 0)\). An auxiliary beam at a wavelength of 935 nm carries out repumping from the \(^{2}{{D}_{{3/2}}}\) state. Rabi oscillations are produced at the \(^{2}{{S}_{{1/2}}}(F = 0) \to {{\;}^{2}}{\kern 1pt} {{D}_{{3/2}}}(F = 2)\) quadrupole transition with a wavelength of 435 nm. This transition is chosen owing to its small width (3 Hz), so that the lifetime of the upper state is much longer than the characteristic dephasing time.

Fig. 2.
figure 2

(Color online) Energy-level diagram of the \(^{{171}}{\text{Y}}{{{\text{b}}}^{ + }}\) ion. Light blue, dark blue, and red arrows show the transitions used for cooling, pumping into the ground state, and repumping, respectively.

Full size image

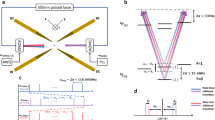
The experiment to measure the parameters of the dephasing of Rabi oscillations is carried out in several stages. First, the ion chain is cooled to a temperature close to the Doppler limit. Then, the ions are pumped into the ground state. Next, all laser sources are turned off, and the system is exposed to the interaction with the environment for some variable time delay. After that, a resonant laser pulse at a wavelength of 435 nm is applied to some selected ion, exciting the quadrupole transition; the duration of this pulse is also varied. Finally, the electron state of this ion is detected by the method of quantum jumps [17].

For a fixed time delay, the population of the upper state of the quadrupole transition is determined as a function of the excitation time. The resulting curve is fitted by Eq. (16), and the value \(\bar {n}(\tau )\), where τ is the time delay, is obtained as one of the fit parameters. This experiment is repeated for several values of τ and the resulting dependence is approximated by a linear function to determine the heating rate (in phonons per second).

To determine the temperature of the ion chain, we simply conduct the above experiment at zero delay, whereby the temperature of the chain can be calculated by the formula

$$T = \frac{{\hbar {{\omega }_{1}}}}{{{{k}_{{\text{B}}}}\ln (1 + 1{\text{/}}\bar {n}(0))}},$$
(17)

where \({{\omega }_{1}}\) is the frequency of the center-of-mass mode (see the previous section) and kB is the Boltzmann constant.

4 EXPERIMENTAL RESULTS

To determine the heating rate, a single ytterbium ion was trapped, so that the products over vibrational modes in Eq. (16) reduce to a single factor each. Since radiation acting on the ion propagates along the trap axis, the relevant vibrational frequency is equal to the axial frequency, and the trap parameters are calculated by the formulas

$${{\eta }_{1}} = \frac{1}{\lambda }\sqrt {\frac{h}{{2m\nu }}} ,\quad {{r}_{1}} = 1,$$
(18)

where λ = 435 nm, m is the mass of the ion, and ν is the frequency of the axial mode in hertz. The results of measurements with a single ion are shown in Fig. 3. The parameters of the fit by Eq. (16) are summarized in Table 1. One can see that, in agreement with the accepted model, the parameter \({{\Omega }_{0}}\) remains approximately constant when the time delay is varied. Furthermore, coefficient a is always close to unity. Its deviation from unity can be explained by the combined influence of the inaccuracy of state preparation and inaccuracy of readout; the readout error during setup calibration was about 10–12%.

Fig. 3.
figure 3

(Color online) (a–e) Population of the ion upper state versus the excitation time for delays of 0, 2, 5, 7, and 10 ms, respectively. (f) Average vibrational quantum number for a single ion versus the time delay.

Full size image
Table 1. Parameters obtained from the fits of Rabi oscillation dephasing curves for a single ion recorded at different time delays τ
Full size table

Approximating the obtained dependence \(\bar {n}(\tau )\) by a linear function, we find the ion heating rate from the slope of this line:

$$\dot {\bar {n}} = (8 \pm 2) \times {{10}^{3}}\;{{{\text{s}}}^{{ - 1}}}.$$
(19)

Deriving Eq. (16), we assumed implicitly that the change in the value of \(\bar {n}\) during the measurements is small. One can see from the obtained value of \(\dot {\bar {n}}\) that the increase in the number of phonons over a 150-µs time interval does not exceed 1–2, which is negligible compared to any value of \(\bar {n}\) observed in the experiment, including the one for zero delay.

We determined the temperature of the chain of five ions. The measurements were performed on the first ion in the chain, so that the trap parameters had the values

$$\begin{gathered} {{\eta }_{k}} = \frac{1}{\lambda }\sqrt {\frac{h}{{2m\nu }}} \\ \times \;\left\{ {0.447, - 0.486,0.346, - 0.173,0.054} \right\}, \\ \end{gathered} $$
(20)
$${{r}_{k}} = \left\{ {1,1.73,2.41,3.05,3.67} \right\}.$$
(21)

The measurement results for the five-ion chain are shown in Fig. 4. The effective average vibrational quantum number obtained from the fit is

$$\bar {n}(0) = 75 \pm 3.$$
(22)
Fig. 4.
figure 4

(Color online) Population of the upper state of the first ion in the chain versus the excitation time.

Full size image

Correspondingly, the temperature of the chain calculated by Eq. (17) is

$$T = 1.69 \pm 0.08\;{\text{mK}}.$$
(23)

The Doppler limit for the transition \(^{2}{{S}_{{1/2}}} \to {{\;}^{2}}{\kern 1pt} {{P}_{{1/2}}}\) is

$${{T}_{{\text{D}}}} = \frac{{\hbar \Gamma }}{{2{{k}_{{\text{B}}}}}} = 0.5\;{\text{mK}}.$$
(24)

The temperature of the chain given by Eq. (23) is close to this limit. The deviation of the actual temperature from the limiting value may result from an increased heating rate compared to the case of a single ion, in particular, from abnormal heating (i.e., heating caused by potential fluctuations at the electrodes and by the location of the ion chain close to the electrode surface).

5 CONCLUSIONS

In summary, we have derived and experimentally verified an analytic expression for the population of the excited state of an ion in a chain as a function of the time of its excitation by resonant radiation, taking into account the thermal distribution over the vibrational degrees of freedom. The experimental results demonstrate that, within the limits of measurement accuracy, the model used in the derivation is valid.

Thus, the proposed method (dephasing of Rabi oscillations) makes it possible to determine both the temperature of the ion chain and the rate of its heating in the trap. The main advantages of this method are its general applicability irrespective of the number of ions in the chain, as well as the fact that, in contrast to the methods mentioned in the Introduction, it can be used for the average phonon numbers \(\bar {n}\) from 50 to 100 and yields adequate results even for heating rates on the order of 104 phonons per second. This widens considerably the range of parameters of chains and traps that can be experimentally determined.