Constraints on Cosmic Rays Population in the Radio Halo of the M87 Galaxy from Gamma-Ray Observations

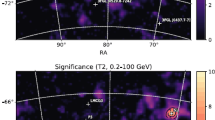
We present results of our search for extended high-energy emission around the M87 galaxy, which is the central galaxy in the Virgo cluster. The M87 galaxy harbors extremely heavy supermassive black hole, ${{M}_{{BH}}} > 4 \times {{10}^{9}}{\kern 1pt} {{M}_{ \odot }}$ and for the last 100 Myr experiences a period of increased activity that resulted in formation of extended lobes, which are prominent radio- and X-ray sources. We perform a search in 13 yr of the Fermi-LAT data in three energy bins: 0.1–1, 1–10, and 10–100 GeV. No significant detection of extended emission was achieved in any bin, with weak indication of a signal ($\sim {\kern 1pt} 2.5\sigma$) in the last bin (10–100 GeV). We used γ-ray observations to put limits on cosmic rays population in the lobes, constraining their fraction X in comparison to the thermal energy of the hot gas. Depending on the value of spectral index, for electrons ${{X}_{e}} < (0.1{-} 0.2)$ and protons were constrained at ${{X}_{p}} < (0.2{-} 0.5)$ level. We confirm that cosmic rays is a subdominant component of the lobes, which are dominated by thermal gas.

1 INTRODUCTION

Powerful outflows interact with surrounding medium and inflate bubbles filled with hot diluted gas and cosmic rays (CRs), eventually transferring energy of the outflows to the medium. In the case of extragalactic sources—active galactic nuclei (AGNs)—this phenomenon observationally manifests itself as lobes around active or past relativistic jets launched by AGNs. Such lobes were observed in large number of sources [1–4], usually in radio and X rays. Study of these lobes is very important because it can help to clarify our understanding of processes of interaction of AGN jets with surrounding medium and to estimate jet powers, using lobes as calorimeters [5]. Observations at higher energies, in γ-ray energy range, could also be very valuable, allowing to probe not only leptonic but also hadronic component of CRs which fill the lobes.

Unfortunately, limited angular resolution¹ and low statistics in the high-energy range make at the present such observations extremely difficult. There are two exceptions: the first is the Cen A galaxy (NGC 5128), belonging to Fanaroff–Riley I (FR I) type. Its proximity to the Earth ($D = 4.7$ Mpc) and large extension of the lobes ($l = 600$ kpc, corresponds to $\theta = 10^\circ$) allowed to detect the lobes as extended objects using the Fermi-LAT observations [6]. Gamma-ray observations indicate the presence of a large population of relativistic electrons, which fill the lobes and experience inverse Compton (IC) scattering on the CMB and EBL (extragalactic background light) photons with possible additional contribution coming from CR protons interacting with diffuse medium of the lobes [7, 8]. Also the γ-ray emission was detected from the lobes of FR I/FR II galaxy Fornax A (NGC 1316, $D = 18.6$ Mpc) [9]. This emission could be of mixed lepto–hadronic origin [9] or be purely leptonic [10].

Another possible candidate for similar detection is the M87 galaxy. Residing at $D = 16.7$ Mpc close to the center of the Virgo cluster it possesses lobes, which were extensively observed in radio and X rays (e.g., [11–15]). The lobes were inflated due to the activity of the AGN in the last 10⁷–10⁸ yr [11]. There is a large difference between M87 and already detected galaxies Cen A and Fornax A: the latter ones reside in a relatively low-density environment, while the former one is situated in the dense core of the massive Virgo galaxy cluster.

The idea of using γ rays from the extended source around M87 in order to probe physical properties of the halo, especially magnetic fields, was first proposed in [16]. The size of the lobes is comparatively small, $l \sim 30$ kpc, at the distance of M87 it corresponds to a radius of 0.1°. This modest angular size makes detection of the halo in γ rays extremely difficult. The strong side of γ-ray observations is their ability to constrain the proton component of CRs, which is much more challenging by other means. Also, the relativistic electrons could be detected due to their IC signature, which in turn could be a useful addition to the detection of the synchrotron emission in radio: although γ-ray observations are less sensitive than radio, the target photon field could be described with much better precision than magnetic fields, eliminating this vital unknown.

In this paper we tried to exploit wealth of information collected by the Fermi LAT, aiming to constrain the extended component. We present our results of this search in 13 yr of Fermi-LAT data at energies higher than 100 MeV and put constraints on CR population in the lobes.

2 DATA AND DATA ANALYSIS

In our analysis, we have used 157 months of Fermi LAT data collected since Aug. 4, 2008 (MET = 239557417 s) until Sep. 5, 2021 (MET = 652552934 s). We have selected events that belong to the “SOURCE” class. The Pass 8R3 reconstruction and Fermitools² and Fermipy [17] were used. We have selected events with energies larger than 100 MeV. Usual event quality cut, namely that the zenith angle should be less than 90° has been imposed.

We took a circle of 15° radius around the position of M87 (${{\alpha }_{{J2000}}} = 187^\circ .706$, ${{\delta }_{{J2000}}} = 12^\circ .391$) as our region of interest (RoI).

The data were analyzed using the binned maximum likelihood approach [18] implemented in the gtlike utility, in which two model hypotheses were compared by their maximal likelihoods with respect to the observed photon distribution. The null hypothesis does not include the extended source, the alternative hypothesis adds the extended source to the list of sources of the null hypothesis.

The model includes 239 sources from the 4FGL-DR2 catalogue [19], the latest galactic interstellar emission model gll_iem_v07.fits, and the isotropic spectral template iso_P8R3_SOURCE_V3_v1.txt.³

The M87 galaxy was modelled as a point source. Finally, spatial templates for extended lobes were inserted into the source model. We have used two alternative models. First, a template obtained from NRAO VLA Sky Survey [20] using SkyView facility [21]. In this template γ-ray brightness follows the radio one and it describes a situation when the radio and γ-ray emission take place in the same regions. That could be the case if the γ-ray emission is produced by IC scattering of the background photons and if the increase in the radio brightness in hotspots could not be solely attributed to the magnetic field amplification. The second adopted template was a uniform shape imitating the shape of the lobes taken from NVSS. This template could naturally arise in scenarios, where CRs are distributed more or less uniformly in the volume of the lobes and is especially relevant for hadronic models.

The M87 point source and the lobe spectra were described by a simple power-law model. The evidence of detection of gamma-ray signal from the lobes was evaluated in terms of a likelihood ratio test statistic:

$$TS = - 2\ln \frac{{{{L}_{{{\text{max}},0}}}}}{{{{L}_{{{\text{max}},1}}}}},$$

(1)

where ${{L}_{{{\text{max}},0}}}$ and ${{L}_{{{\text{max}},1}}}$ are the maximum likelihood values obtained from the observed data fit using null and alternative hypothesis, respectively. If the alternative hypothesis is true, then $\sqrt {TS}$ is approximately equivalent to the source detection significance.

In order to evaluate potential sensitivity of our searches we have performed simulations using gtobssim utility. We have simulated events for isotropic and galactic backgrounds, brightest sources (185 total in 15°) and either M87 as a point source with a flux equal to the value from the 4FGL-DR2 catalog, or extended source with the same flux which follows one of the two aforementioned templates. This approach makes possible to test limiting sensitivity: what would be the difference in LLH between the models with the point source only and the point source plus the extended source if all the flux actually came from the extended source, is it possible to distinguish between the null and alternative hypotheses?

3 RESULTS

Our analysis of gamma-ray data could not detect the extended sources at the location of M87 in neither of the three sub-intervals (0.1–1, 1–10, 10–100 GeV). Only in the last one we obtained some marginal indication at 2.5σ level ($TS = 6.2$). The negative result is probably due to the compactness of the halo around M87: its size is only about 0.1° and the 68% containment angle of LAT at 100 MeV is about 5°. At higher energies, the photon statistics becomes insufficient. Even when we simulated M87 as an extended source with the flux taken from 4FGL, the fit with a point source was just as good as that with an extended one for bins 0.1–1 and 1–10 GeV. Interestingly, for the last energy bin, 10–100 GeV, this setup lead to $5.6\sigma$ detection ($TS2$). Weak detection of the extended component at $2\sigma$-level was observed when the total flux in the simulation was equally split between the point source and the halo. Non-detection of extended component forced us to use the measurement of M87 flux provided by 4FGL as the upper limit for the flux from the halo.

Gamma-ray observations can be used to put constraints on the properties of the lobes, such as magnetic field strength and CR energy density. Radio observations show that there is a population of relativistic leptons in the lobes which produce synchrotron radiation. The very same population will interact with photons of the background with energies E_bckg and produce photons of higher energy E_γ ~ γ² E_bckg, where γ is the Lorentz factor of relativistic leptons. Specifically, γ rays are produced when leptons interact with photons of NIR-UV background coming from M87. In what follows, we will refer to this background photons as optical ones.

3.1 Constraint on the Magnetic Field

We can exclude certain values of the magnetic field B: we infer properties of the lepton population which could produce the observed radio flux at the fixed value of B. If the IC signal from this population is higher than the observed γ-ray flux, then that value of B could serve as a lower limit on the strength of the magnetic field.

We suppose that the same population of non-thermal electrons produce both the synchrotron radiation in the magnetic field filling the lobes and the inverse Compton radiation due to the presence of the background light from the galaxy. To make a theoretical estimation of the gamma-ray flux from the lobes, one needs to know the spectrum of the non-thermal electrons and the energy density of the background radiation field. The electron spectrum can be obtained from the radio observations of the synchrotron radiation. Its spectrum in the range of 100 MHz–10 GHz is given in [22]. If the electron spectrum is of the form

$$N(E)dE = {{C}_{e}}{{E}^{{ - {{\alpha }_{e}}}}}dE\;[{\text{c}}{{{\text{m}}}^{{ - 3}}}]$$

(2)

then the energies of non-thermal electrons producing the synchrotron radiation are in the range [23]:

$$\begin{gathered} 2.5 \times {{10}^{2}}{{\left( {\frac{{{{\nu }_{1}}}}{{B{{y}_{1}}({{\alpha }_{e}})}}} \right)}^{{1/2}}} \\ \leqslant E\;({\text{eV}}) \leqslant 2.5 \times {{10}^{2}}{{\left( {\frac{{{{\nu }_{2}}}}{{B{{y}_{2}}({{\alpha }_{e}})}}} \right)}^{{1/2}}}, \\ \end{gathered} $$

(3)

where B is the magnetic field, ${{\nu }_{1}}$ and ${{\nu }_{2}}$ are the minimum and maximum frequencies of the radio spectrum, ${{y}_{1}}$ and ${{y}_{2}}$ are tabulated functions. These functions together with $a({{\alpha }_{e}})$ below are given in [23]. From the synchrotron spectrum, we can obtain the normalization of the electron spectrum [23]:

$${{C}_{e}} = \frac{{7.4 \times {{{10}}^{{21}}}{{D}^{2}}}}{{a({{\alpha }_{e}})BV}}{{\Phi }_{\nu }}{{\left( {\frac{\nu }{{6.26 \times {{{10}}^{{18}}}B}}} \right)}^{{({{\alpha }_{e}} - 1)/2}}},$$

(4)

where V is the volume which contains the emitting particles, D is the distance to M87, and ${{\Phi }_{\nu }}$ is the synchrotron flux at the frequency ν. Since we use the synchrotron data integrated over the radio halo, we will assume in this subsection, that the non-thermal electron distribution is homogeneous, so that the normalization ${{C}_{e}}$ is constant throughout the halo. We approximate the optical radiation energy density at a distance r from the galaxy center with that of a point source:

$${{U}_{{{\text{rad}}}}}(r) = \frac{L}{{4\pi {{r}^{2}}c}},$$

(5)

where L is the optical luminosity of the galaxy. To estimate L, we used the data of the Sloan Digital Sky Survey (SDSS) since its ugriz magnitudes have absolute calibration. The SDSS data are reported to strongly underestimate the brightness of large extended sources [24], therefore we used the corrected magnitudes from the cited work: $u = 10.98$, $g = 9.42$, $r = 8.61$, $i = 8.16$, $z = 7.86$. The power of the inverse-Compton radiation per single electron is [25]:

$${{P}_{{{\text{IC}}}}} = \frac{4}{3}{{\sigma }_{{\text{T}}}}c{{U}_{{{\text{rad}}}}}{{\gamma }^{2}}{{\beta }^{2}},$$

(6)

where σ_T is the Thomson scattering cross section, $\gamma$ is the electron Lorentz factor, and $\beta = v{\text{/}}c \approx 1$. Using our expressions for the radiation and electron energy density, we obtain the total power of the inverse Compton radiation:

$$\begin{gathered} {{P}_{{{\text{tot}}}}} = \iint \frac{4}{3}{{\sigma }_{{\text{T}}}}c{{\gamma }^{2}}\frac{L}{{4\pi {{r}^{2}}c}}{{C}_{e}}(B){{E}^{{ - {{\alpha }_{e}}}}}dVdE \\ = \frac{4}{3}{{\sigma }_{{\text{T}}}}\frac{{{{C}_{e}}(B)}}{{{{{({{m}_{e}}{{c}^{2}})}}^{2}}}}LR\int {{E}^{{2 - {{\alpha }_{e}}}}}dE, \\ \end{gathered} $$

(7)

where $R = 35$ kpc is the value we adopt for the radius of the halo [11]. One can see that the result depends implicitly on the magnetic field. For $B < 1.5{\kern 1pt}$ μG, the resulting gamma-ray energy flux becomes larger than that observed from M87 (F = 1.8 × 10^–11 erg/cm² above 100 MeV), thus these values could be excluded.

3.2 Constraints on the Non-Thermal Electron Content

Most of the energy of the lobes is thermal, i.e., stored in the kinetic energy of a hot (~2 keV) diluted gas [26]. Energy fraction in the CRs is subdominant, nevertheless it could play important role in the evolution of the lobes. It also could be constrained from the γ-ray observations.

For lepton-dominated models, the γ-ray flux would emerge due to the IC scattering on the photons of optical background. We have used the so-called isobaric approximation where the energy density of non-thermal electrons is a constant fraction ${{X}_{e}}$ of the thermal energy. In the hot X-ray gas, ion and electron densities are approximately equal, thus the thermal energy density is ${{\epsilon }_{{{\text{th}}}}} \approx 3{{n}_{e}}kT$, where ${{n}_{e}}$ and T are the number density and temperature of the thermal electrons, respectively. For these parameters, we use analytical models derived in [26]. Let ${{C}_{e}}{{E}^{{ - {{\alpha }_{e}}}}}$ describe the non-thermal electron density per unit volume per unit energy; then

$${{X}_{e}} = \frac{{{{C}_{e}}(r)\int {{E}^{{1 - {{\alpha }_{e}}}}}dE}}{{3{{n}_{e}}(r)kT(r)}},$$

(8)

where r is the distance from the core. The total power of the IC-emitting volume is [25]:

$${{P}_{{{\text{IC}}}}} = \iint \frac{4}{3}{{\sigma }_{{\text{T}}}}c{{U}_{{{\text{rad}}}}}(r)\frac{{{{C}_{e}}}}{{{{{({{m}_{e}}{{c}^{2}})}}^{2}}}}{{E}^{{2 - {{\alpha }_{e}}}}}dEdV.$$

(9)

Substituting Eq. (8) we obtain the expression for ${{X}_{e}}$:

$${{X}_{e}} = \frac{{4\pi {{D}^{2}}F{{{({{m}_{e}}{{c}^{2}})}}^{2}}}}{{4{{\sigma }_{{\text{T}}}}L}}\frac{{\int {{E}^{{1 - {{\alpha }_{e}}}}}dE}}{{\int {{E}^{{2 - {{\alpha }_{e}}}}}dE}}\frac{1}{{\int {{n}_{e}}kTdr}},$$

(10)

where we used Eq. (5) for ${{U}_{{{\text{rad}}}}}$. Lorentz factor of the electrons scattering photons from ~1 eV to ~100 MeV is of order 10⁴. If we use this value as ${{\gamma }_{{{\text{min}}}}}$ then ${{X}_{e}}$ falls in the range 0.45–0.67% when ${{\alpha }_{e}}$ varies from 2.5 to 3.5. Integrating the thermal energy density from the galaxy center up to a distance of 35 kpc (or 7 arcmin of angular distance) we obtain the total energy ${{E}_{{{\text{th}}}}} = 4.7 \times {{10}^{{59}}}$ erg.

3.3 Constraint on the Non-Thermal Proton Content

Similar constraints could be put on the hadronic component as well. Now gamma rays are produced in p–p (and p–He) collisions of CR protons with kinetic energies larger than threshold 280 MeV followed by neutral pion decay. Gamma-ray emissivity is

$${{q}_{\gamma }}({{E}_{\gamma }}) = 2\int\limits_{{{E}_{\gamma }} + m_{\pi }^{2}{{c}^{4}}/4{{E}_{\gamma }}}^\infty {\frac{{{{q}_{\pi }}({{E}_{\pi }})}}{{\sqrt {E_{\pi }^{2} - m_{\pi }^{2}{{c}^{4}}} }}} d{{E}_{\pi }},$$

(11)

where ${{q}_{\pi }}({{E}_{\pi }})$ is the ${{\pi }^{0}}$ production rate. In the delta-function approximation, the energy of a pion produced in a p–p collision is equal to a fixed fraction of   the proton kinetic energy: ${{E}_{\pi }} = {{\kappa }_{\pi }}{{E}_{{{\text{kin}}}}}$, where ${{\kappa }_{\pi }} \approx 0.17$ is the inelasticity parameter. Under this simplification, the pion production rate can be written:

$${{q}_{\pi }}({{E}_{\pi }}) = \frac{{c{{n}_{H}}}}{{{{\kappa }_{\pi }}}}{{\sigma }_{{pp}}}\left( {{{m}_{p}}{{c}^{2}} + \frac{{{{E}_{\pi }}}}{{{{\kappa }_{\pi }}}}} \right){{N}_{p}}\left( {{{m}_{p}}{{c}^{2}} + \frac{{{{E}_{\pi }}}}{{{{\kappa }_{\pi }}}}} \right),$$

(12)

where ${{n}_{H}}$ is the ambient proton density (we assume ${{n}_{H}} \approx {{n}_{e}}$), ${{\sigma }_{{pp}}}$ is the ${{\pi }^{0}}$ creation cross-section, and ${{N}_{p}} = {{C}_{p}}{{E}^{{ - {{\alpha }_{p}}}}}$ is the cosmic ray proton spectrum. Now, the ratio of the non-thermal protons to the thermal energy density is

$${{X}_{p}} = \frac{{{{C}_{p}}(r)\int {{E}^{{1 - {{\alpha }_{p}}}}}dE}}{{3{{n}_{e}}(r)kT(r)}}.$$

(13)

Substituting Eqs. (12) and (13) into Eq. (11), we get

$${{Q}_{\gamma }} = \int {{q}_{\gamma }}dV = \frac{{6c{{X}_{p}}}}{{{{\kappa }_{\pi }}}}$$

$$ \times \;\int \frac{{{{\sigma }_{{pp}}}({{m}_{p}}{{c}^{2}} + {{E}_{\pi }}{\text{/}}{{\kappa }_{\pi }})}}{{\sqrt {E_{\pi }^{2} - m_{\pi }^{2}{{c}^{4}}} }}{{({{m}_{p}}{{c}^{2}} + {{E}_{\pi }}{\text{/}}{{\kappa }_{\pi }})}^{{ - {{\alpha }_{p}}}}}d{{E}_{\pi }}$$

(14)

$$ \times \;\frac{1}{{\int {{E}^{{ - {{\alpha }_{p}} + 1}}}dE}}\int 4\pi {{r}^{2}}{{n}_{e}}{{(r)}^{2}}kT(r)dr.$$

Again, we take $4\pi {{D}^{2}}F = \int {{Q}_{\gamma }}d{{E}_{\gamma }}$ as if the gamma-ray flux of M87 was entirely of hadronic origin. For the proton spectrum index from 2.1 to 2.5, we obtain ${{X}_{p}}$ from 0.23 to 0.53 and the total non-thermal energy in CR protons E_{p, non-th} < (1–2) × 10⁵⁹ erg.

4 DISCUSSION AND CONCLUSIONS

Results show that for $\gamma {{ > 10}^{4}}$, X_e < (4–6) × 10^–3 depending on the spectral index of relativistic electrons distribution. We emphasize that the value obtained in Section 3.2 refers to the electron population responsible for the IC gamma radiation above 100 MeV. As shown in Section 3.2, these electrons have $\gamma {{ > 10}^{4}}$ and probably constitute only a part of the non-thermal electron population. The estimation of the whole electron contribution and not only its high-energy part is much more uncertain. First, we do not know the lower limit ${{\gamma }_{{\min }}}$ on the γ, which could be in the range of 10–100 [12]. Second, the spectral index for electron population that can be inferred from radio observations is rather steep, ${{\alpha }_{e}} \sim 3$ [12] but it can be mostly representative for regions of active synchrotron emission. In a realistic scenario, the medium in the lobes is non-uniform: most of the volume is permeated by the weak magnetic field, while emission mostly takes place in the filaments where the field is stronger; electrons spend most of their lifetime outside of these filaments and fast depletion of high-energy electrons inside the filaments could lead to distortions in the electron particle spectrum restored from the radio observations [11].

Given the uncertainty in the electron spectrum, we calculated ${{X}_{e}}$ for a number of spectral parameter combinations. The results are shown in Table 1. One can see that if the spectrum of the electrons of the lowest energies is not too steep or/and the low-energy cut-off is greater than 10², the total electron fraction ${{X}_{e}} \leqslant 0.2$.

Table 1. Values of ${{X}_{e}}$ for different combinations of the spectral index and low-energy cutoff of the electron spectrum. $\gamma = {{10}^{4}}$ corresponds to the lower energy of the electrons upscattering background photons from ~1 eV to ~100 MeV

If we take estimates for the lobes field as $B = 10$ μG [11, 12] and ${{X}_{e}} = 0.1$ as a benchmark, then the ratio of energies would be ${{U}_{e}}{\text{/}}{{U}_{B}} < 2.5$, showing that the electrons could be close to equipartition. However, as discussed above, the mean value for the field strength could be lower, as $B = 10$ μG estimate is relevant for filaments, or ${{X}_{e}}$ could be higher. Then the ratio ${{U}_{e}}{\text{/}}{{U}_{B}}$ could be as high as $\mathcal{O}(10)$, the level that is actually inferred for lobes of powerful FR II galaxies [4].

Our estimations could be compared with ones from radio observations, where the total electron energy is estimated using equipartition assumption. Electron fraction ${{X}_{e}}$ was also found to be close to $\mathcal{O}(0.1)$, exact value depended on assumed ${{\gamma }_{{\min }}}$ [12].

Proton contribution is much more elusive and we were able to constrain them at somewhat higher level X_p < 0.2–0.5. This is a slightly weaker constraint than that obtained in [26], where total contribution of relativistic particles was constrained to be less than 10%.

Further progress in this area would be achieved with the advent of new observational facilities. First, observations with future MeV range telescopes such as AMEGO-X [27] with degree angular resolution could possibly strongly constrain the extended contribution to observed signal from M87, thus severely tightening limits on IC emission from relativistic electrons. Second, deep observation of the CTA in >100 GeV energy range and search for an extended component could give valuable constraints on hadronic population of the lobes.