Recent measurement of the muon magnetic moment at Fermilab has confirmed the deviation from the Standard Model prediction [1]. When averaged with the previous BNL result [2], it leads to a discrepancy of more than four standard deviations [1]. If it is a manifestation of New Physics, one should expect that at higher energies the deviations in the interactions of muons from the Standard Model predictions should be larger. Since ultraperipheral collisions are a source of very clean events, they can help to constrain parameters of new particles that can be responsible for this difference, e.g., see [3, 4].

At the Large Hadron Collider (LHC), muon pairs are produced with high invariant masses, and this gives a chance for New Physics to be detected. It follows that the theoretical description of these reactions in the Standard Model is highly desirable. Recently, the ATLAS collaboration has measured the fiducial cross section for the process when a muon pair is accompanied by the detection of one of the colliding protons in the forward detector [5]. Here, we provide expressions for the cross section for this reaction. Using the derived formulas, the cross section values can be evaluated by the standard numerical integration routines (e.g., provided by the GSL [6]) rather than Monte Carlo simulations. Let us note that numerical results for this reaction were recently presented in [7] (see also [8]).

The master formula describing the reaction under consideration can be easily obtained from the expressions provided in the review of two-photon particle production [9]:

$$d{{\sigma }_{{pq \to p{{\mu }^{ + }}{{\mu }^{ - }}q}}} = \frac{{Q_{q}^{2}{{{(4\pi \alpha )}}^{2}}}}{{{{{(q_{1}^{2})}}^{2}}{{{(q_{2}^{2})}}^{2}}}}(q_{1}^{2}\rho _{{\mu \nu }}^{{(1)}})(q_{2}^{2}\rho _{{\alpha \beta }}^{{(2)}}){{M}_{{\mu \alpha }}}M_{{\nu \beta }}^{*}$$
$$ \times \;\frac{{{{{(2\pi )}}^{4}}{{\delta }^{{(4)}}}({{q}_{1}} + {{q}_{2}} - {{k}_{1}} - {{k}_{2}})d\Gamma }}{{4\sqrt {{{{({{p}_{1}}{{p}_{2}})}}^{2}} - m_{p}^{4}} }}$$
(1)
$$ \times \;\frac{{{{d}^{3}}p_{1}^{'}}}{{{{{(2\pi )}}^{3}}2E_{1}^{'}}}\frac{{{{d}^{3}}p_{2}^{'}}}{{{{{(2\pi )}}^{3}}2E_{2}^{'}}},$$

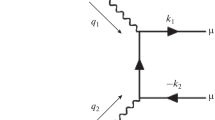
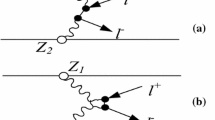
where α is the fine structure constant, \({{Q}_{q}}\) is the electric charge of the quark q, \(\rho _{{\mu \nu }}^{{(1)}}\) and \(\rho _{{\alpha \beta }}^{{(2)}}\) are the density matrices of the photons, \({{M}_{{\mu \alpha }}}\) is the amplitude of the process, \({{p}_{1}}\), \(p_{1}^{'}\), \({{p}_{2}}\), \(p_{2}^{'}\) are the proton and quark momenta before and after the collision (see Fig. 1), \({{k}_{1}}\) and \({{k}_{2}}\) are the momenta of muons, \({{q}_{1}}\) and \({{q}_{2}}\) are the momenta of photons, \(E_{1}^{'}\) and \(E_{2}^{'}\) are the proton and quark energies in the final state, \(d\Gamma \) is the phase volume of the muon pair, and \({{m}_{p}}\) is the proton mass. For the density matrices, we get

$$\begin{gathered} \rho _{{\mu \nu }}^{{(1)}} = - \frac{1}{{2q_{1}^{2}}}{\text{Tr}}\{ (\hat {p}_{1}^{'} + {{m}_{p}}){{\gamma }_{\mu }}({{{\hat {p}}}_{1}} + {{m}_{p}}){{\gamma }_{\nu }}\} \\ = - \left( {{{g}_{{\mu \nu }}} - \frac{{{{q}_{{1\mu }}}{{q}_{{1\nu }}}}}{{q_{1}^{2}}}} \right) - \frac{{{{{(2{{p}_{1}} - {{q}_{1}})}}_{\mu }}{{{(2{{p}_{1}} - {{q}_{1}})}}_{\nu }}}}{{q_{1}^{2}}}, \\ \end{gathered} $$
(2)

and a similar expression for \(\rho _{{\alpha \beta }}^{{(2)}}\).

Fig. 1.
figure 1

Photon–photon fusion mechanism of muon pair production.

Full size image

In order for the proton to remain intact, the square of the momentum transfer \( - q_{1}^{2}\) should be bounded from above: \( - q_{1}^{2} \lesssim {{\hat {q}}^{2}}\), where \(\hat {q} \sim {{\Lambda }_{{QCD}}}\). Following [10], we take \(\hat {q} = 200\) MeV in our calculations below. In this case, if the energy carried by the photon is in the interval \(0.015{{E}_{p}} < {{\omega }_{1}} < 0.15{{E}_{p}}\) then the proton will be detected by the forward detector with near 100% efficiency [11, 12]. As for the quark, its value of the transferred momentum \( - q_{2}^{2}\) is approximately bounded by the invariant mass of the muon pair W, because the cross section for the reaction \(\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}\) at \( - q_{2}^{2} > {{W}^{2}}\) decreases rapidly as \({{W}^{2}}{\text{/}}( - q_{2}^{2})\). Thus the photon with the momentum \({{q}_{1}}\) is emitted quasi-elastically and is polarized transversally, while the photon with the momentum \({{q}_{2}}\) can also be longitudinally polarized.Footnote 1

The most appropriate way to deal with the density matrices \(\rho _{{\mu \nu }}^{{(1)}}\) and \(\rho _{{\alpha \beta }}^{{(2)}}\) is to introduce the basis of virtual photons helicity states. Let us suppose that in the center-of-mass system (c.m.s.) of the colliding photons we have \({{q}_{1}} = ({{\widetilde \omega }_{1}},0,0,{{\widetilde q}_{1}})\) and \({{q}_{2}} = ({{\widetilde \omega }_{2}},0,0, - {{\widetilde q}_{1}})\). The standard set of orthonormal four-vectors orthogonal to the momenta \({{q}_{1}}\), \({{q}_{2}}\) is

$$e_{\mu }^{{(1)}}( + 1) = \frac{1}{{\sqrt 2 }}(0, - 1, - i,0),$$
$$e_{\mu }^{{(1)}}( - 1) = \frac{1}{{\sqrt 2 }}(0,1, - i,0),$$
$$\begin{gathered} e_{\mu }^{{(1)}}(0) = \frac{i}{{\sqrt { - q_{1}^{2}} }}({{\widetilde q}_{1}},0,0,{{\widetilde \omega }_{1}}), \\ e_{\mu }^{{(2)}}( + 1) = \frac{1}{{\sqrt 2 }}(0,1, - i,0), \\ \end{gathered} $$
(3)
$$e_{\mu }^{{(2)}}( - 1) = \frac{1}{{\sqrt 2 }}(0, - 1, - i,0),$$
$$e_{\mu }^{{(2)}}(0) = \frac{i}{{\sqrt { - q_{2}^{2}} }}( - {{\widetilde q}_{1}},0,0,{{\widetilde \omega }_{2}}).$$

These four-vectors correspond to the ±1 and 0 helicity states of virtual photons in their c.m.s. They form a complete orthonormal basis for subspaces orthogonal to \({{q}_{{1\mu }}}\) and \({{q}_{{2\mu }}}\), respectively. Taking into account, that, due to the conservation of the vector currents, \(\rho _{{\mu \nu }}^{{(1)}}{{q}_{{1\mu }}} = \rho _{{\mu \nu }}^{{(2)}}{{q}_{{2\mu }}}\) = 0, we obtain

$$\begin{gathered} \rho _{{\mu \nu }}^{{(i)}} = \sum\limits_{a,b} \text{[}e_{\mu }^{{(i)}}(a)]{\text{*}}e_{\nu }^{{(i)}}(b)\rho _{{ab}}^{{(i)}},\quad a,b = \pm 1,0, \\ \rho _{{ab}}^{{(i)}} = ( - {{1)}^{{a + b}}}e_{\mu }^{{(i)}}(a)[e_{\nu }^{{(i)}}(b)]{\text{*}}\rho _{{\mu \nu }}^{{(i)}}. \\ \end{gathered} $$
(4)

Here, \(\rho _{{ab}}^{{(i)}}\) are the density matrices in the helicity representation, and, according to [14], in the c.m.s. system of colliding protons in the case \(E \gg {{\omega }_{1}}\), \(xE \gg {{\omega }_{2}}\) we haveFootnote 2

$$\begin{gathered} \rho _{{ + + }}^{{(1)}} = \rho _{{ - - }}^{{(1)}} = 2\frac{{{{E}^{2}}}}{{\omega _{1}^{2}}},\quad \rho _{{00}}^{{(1)}} = 4\frac{{{{E}^{2}}}}{{\omega _{1}^{2}}}, \\ \rho _{{ + + }}^{{(2)}} = \rho _{{ - - }}^{{(2)}} = 2\frac{{{{x}^{2}}{{E}^{2}}}}{{\omega _{2}^{2}}},\quad \rho _{{00}}^{{(2)}} = 4\frac{{{{x}^{2}}{{E}^{2}}}}{{\omega _{2}^{2}}}, \\ \end{gathered} $$
(5)

where \(E \equiv \sqrt s {\text{/}}2\) = 6.5 TeV is the colliding proton energy while \(xE\) is the quark energy, \(0 < x < 1\).

Finally, we obtain

$$d{{\sigma }_{{pq \to p{{\mu }^{ + }}{{\mu }^{ - }}q}}} = {{(4\pi \alpha )}^{2}}Q_{q}^{2}\frac{{4({{q}_{1}}{{q}_{2}})}}{{4({{p}_{1}}{{p}_{2}})}}{{\sigma }_{{\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}}}}(q_{2}^{2},W)$$
$$\begin{gathered} \times \;4 \times 2{{\left( {\frac{E}{{{{\omega }_{1}}}}} \right)}^{2}} \times 2{{\left( {\frac{{xE}}{{{{\omega }_{2}}}}} \right)}^{2}}\frac{{\frac{1}{2}dq_{{1 \bot }}^{2}d{{\omega }_{1}}}}{{{{{(2\pi )}}^{4}}q_{1}^{2}}}\frac{{\frac{1}{2}dq_{{2 \bot }}^{2}d{{\omega }_{2}}}}{{(4x{{E}^{2}})q_{2}^{2}}} \\ = {{\left( {\frac{\alpha }{\pi }} \right)}^{2}}Q_{q}^{2}\frac{{({{q}_{1}}{{q}_{2}})}}{{({{p}_{1}}{{p}_{2}})}}{{\sigma }_{{\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}}}}(q_{2}^{2},W)x{{E}^{2}} \\ \end{gathered} $$
(6)
$$ \times \;\frac{{dq_{{1 \bot }}^{2}}}{{q_{1}^{2}}}\frac{{dq_{{2 \bot }}^{2}}}{{q_{2}^{2}}}\frac{{d{{\omega }_{1}}}}{{\omega _{1}^{2}}}\frac{{d{{\omega }_{2}}}}{{\omega _{2}^{2}}},$$

where \(({{p}_{1}}{{p}_{2}}) = 2{{E}^{2}}x\), \(({{q}_{1}}{{q}_{2}}) = ({{W}^{2}} - q_{2}^{2}){\text{/}}2\),

$$d{{\sigma }_{{\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}}}} = \frac{{\sum \overline {{\text{|}}M{{{\text{|}}}^{2}}} d\cos \theta }}{{32\pi {{W}^{2}}(1 - q_{2}^{2}{\text{/}}{{W}^{2}})}},$$
$$\begin{gathered} \sum \overline {{\text{|}}M{{{\text{|}}}^{2}}} = \frac{1}{4}[{\text{|}}{{M}_{{ + + }}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ + - }}}{{{\text{|}}}^{2}} \\ + \;{\text{|}}{{M}_{{ - + }}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ - - }}}{{{\text{|}}}^{2}} + 2{\text{|}}{{M}_{{ + 0}}}{{{\text{|}}}^{2}} + 2{\text{|}}{{M}_{{ - 0}}}{{{\text{|}}}^{2}}], \\ \end{gathered} $$
(7)

\({{M}_{{ \pm \pm }}}\) and \({{M}_{{ \pm 0}}}\) are the amplitudes of the process \(\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}\) with the corresponding photons polarizations. According to Eq. (E.3) from [9],

$${{\sigma }_{{TT}}} \equiv \int \frac{1}{4}[{\text{|}}{{M}_{{ + + }}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ + - }}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ - + }}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ - - }}}{{{\text{|}}}^{2}}]$$
$$ \times \;\frac{{d\cos \theta }}{{32\pi {{W}^{2}}(1 - q_{2}^{2}{\text{/}}{{W}^{2}})}}$$
$$ \approx \frac{{4\pi {{\alpha }^{2}}}}{{{{W}^{2}}}}\left[ {\frac{{1 + q_{2}^{4}{\text{/}}{{W}^{4}}}}{{{{{(1 - q_{2}^{2}{\text{/}}{{W}^{2}})}}^{3}}}}\ln \frac{{{{W}^{2}}}}{{{{m}^{2}}}} - \frac{{{{{(1 + q_{2}^{2}{\text{/}}{{W}^{2}})}}^{2}}}}{{{{{(1 - q_{2}^{2}{\text{/}}{{W}^{2}})}}^{3}}}}} \right],$$
$$\begin{gathered} {{\sigma }_{{TS}}} \equiv \int \frac{1}{2}[{\text{|}}{{M}_{{ + 0}}}{{{\text{|}}}^{2}} + \;{\text{|}}{{M}_{{ - 0}}}{{{\text{|}}}^{2}}]\frac{{d\cos \theta }}{{32\pi {{W}^{2}}(1 - q_{2}^{2}{\text{/}}{{W}^{2}})}} \\ \approx \frac{{16\pi {{\alpha }^{2}}{{W}^{2}}( - q_{2}^{2})}}{{{{{({{W}^{2}} - q_{2}^{2})}}^{3}}}}, \\ \end{gathered} $$
(8)

where m is the muon mass. Thus, \({{\sigma }_{{\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}}}} = \) \({{\sigma }_{{TT}}} + {{\sigma }_{{TS}}}\) should be substituted into Eq. (6).

Integration over \(q_{{1 \bot }}^{2}\) in Eq. (6) is easily performed: \(\int dq_{{1 \bot }}^{2}{\text{/}}q_{1}^{2} = 2\ln \hat {q}\gamma {\text{/}}{{\omega }_{1}}\), where \(\gamma = E{\text{/}}{{m}_{p}}\) is the Lorentz factor of the proton. In the c.m.s. of the protons, the following equations hold:

$${{q}_{2}} = \left( {{{\omega }_{2}},{{q}_{{2 \bot }}},\frac{{{{E}_{q}}}}{{{{p}_{q}}}}{{\omega }_{2}}} \right),\quad q_{2}^{2} = - \frac{{\omega _{2}^{2}}}{{{{x}^{2}}{{\gamma }^{2}}}} - q_{{2 \bot }}^{2},$$
$${{q}_{1}}{{q}_{2}} = {{\omega }_{1}}{{\omega }_{2}}\left( {1 + \frac{{{{E}_{q}}}}{{{{p}_{q}}}}} \right) \approx 2{{\omega }_{1}}{{\omega }_{2}},\quad {{W}^{2}} = 4{{\omega }_{1}}{{\omega }_{2}} + q_{2}^{2},$$

where \({{E}_{q}}\) and \({{p}_{q}}\) are the quark energy and spatial momentum: \({{p}_{2}} = ({{E}_{q}},{{p}_{q}})\).

It is convenient to change the integration variables from the photon energies \({{\omega }_{1}}\) and \({{\omega }_{2}}\) to the square of the invariant mass of the produced pair \({{W}^{2}}\) and the ratio of photon energies \(y = {{\omega }_{1}}{\text{/}}{{\omega }_{2}}\): \(d{{\omega }_{1}}d{{\omega }_{2}}dq_{{2 \bot }}^{2}\) = \((1{\text{/}}8y)d{{W}^{2}}dydQ_{2}^{2}\), where \(Q_{2}^{2} = - q_{2}^{2}\). The following upper bounds on photon energies should be taken into account: \({{\omega }_{1}} \leqslant \hat {q}\gamma \), \({{\omega }_{2}} \leqslant xE\). Thus, we obtain

$${{\sigma }_{{pp \to p{{\mu }^{ + }}{{\mu }^{ - }}X}}} = 2{{\left( {\frac{\alpha }{\pi }} \right)}^{2}}\sum\limits_q Q_{q}^{2}\int\limits_{{{{\hat {W}}}^{2}}}^\infty d{{W}^{2}}$$
$$\begin{gathered} \times \;\int\limits_0^{s\hat {q}/{{m}_{p}} - {{W}^{2}}} \frac{{{{\sigma }_{{\gamma \gamma \text{*} \to {{\mu }^{ + }}{{\mu }^{ - }}}}}(Q_{2}^{2},{{W}^{2}})}}{{{{W}^{2}} + Q_{2}^{2}}}dQ_{2}^{2} \\ \times \;\int\limits_{\frac{{{{W}^{2}} + Q_{2}^{2}}}{{s\hat {q}/{{m}_{p}}}}}^1 {{f}_{q}}(x,Q_{2}^{2})dx \\ \end{gathered} $$
(9)
$$ \times \;\int\limits_{({{W}^{2}} + Q_{2}^{2})/{{x}^{2}}s}^{{{{(2\hat {q}\gamma )}}^{2}}/({{W}^{2}} + Q_{2}^{2})} \frac{{dy}}{y}\frac{{\ln (\hat {q}\gamma {\text{/}}{{\omega }_{1}})}}{{Q_{2}^{2} + {{{({{\omega }_{2}}{\text{/}}x\gamma )}}^{2}}}},$$

where \({{\omega }_{1}} = \sqrt {y({{W}^{2}} + Q_{2}^{2})} {\text{/}}2\), \({{\omega }_{2}} = \sqrt {{{W}^{2}} + Q_{2}^{2}} {\text{/}}(2\sqrt y )\) and \({{f}_{q}}(x,Q_{2}^{2})\) is the q-quark density function. Here, the sum is taken over all quarks and antiquarks, both valent (u, d) and sea. The factor of 2 takes into account the symmetrical process, when the proton from the second vertex remains intact. The differential cross section \(d{{\sigma }_{{pp \to p{{\mu }^{ + }}{{\mu }^{ - }}X}}}{\text{/}}dW\) for \(W > 12\) GeV is shown in Fig. 2. Quark density functions were taken from the set MMHT2014nnlo68cl [15] of the LHAPDF library [16]. The integrated cross section in this region is

$${{\sigma }_{{pp \to p{{\mu }^{ + }}{{\mu }^{ - }}X}}}(W > 12\;{\text{GeV}}) = 203\;{\text{pb}}.$$
(10)
Fig. 2.
figure 2

Spectrum \(d{{\sigma }_{{pp \to p{{\mu }^{ + }}{{\mu }^{ - }}X}}}{\text{/}}dW\) of muon pairs produced in the fusion of photons with one forward proton.

Full size image

It is instructive to compare this result with the cross section for quasielastic \({{\mu }^{ + }}{{\mu }^{ - }}\) pair production [10]:

$${{\sigma }_{{pp \to p{{\mu }^{ + }}{{\mu }^{ - }}p}}}(W > 12\;{\text{GeV}}) = 60\;{\text{pb}}.$$
(11)

Let us mention [17, 18] in which the case of lepton pair production in photon fusion with both protons scattered inelastically is studied.

CONCLUSIONS

The cross section for \({{\mu }^{ + }}{{\mu }^{ - }}\) pair production in semi-inclusive pp-scattering at the LHC is calculated (see Eqs. (9) and (10)). The spectrum of the produced pairs is presented in Fig. 2. Taking into account the dependence of differential cross section on photon virtuality explicitly, we have achieved better accuracy in comparison to the equivalent photon approximation.