Broadband Whistler Waves and Differential Electron Fluxes in the Equatorial Region of the Magnetosphere behind the Plasmapause during Substorm Injections

Abstract

This paper considers the whistler waves in the frequency band from 3 to 30 kHz observed on the Van Allen Probe-B satellite on March 17, 2019, when the satellite was on L-shells from 2.8 to 5.4. The upper frequency in the emission spectrum followed the course of the electron gyrofrequency ${{f}_{{ce}}}$ and was lower than it by 1–5 kHz. The emission spectrum often had two spectral maxima (above and below f_ce/2); the maximum at frequencies above f_ce/2 could be either more or less intense. High-frequency whistler waves at frequencies > f_ce/2 were observed simultaneously with an increase in low-energy electron fluxes with energies more than 10² eV, which had transverse anisotropy. To explain the observed spectrum, we used simultaneous satellite measurements of the cold plasma density and differential fluxes of energetic electrons in the energy range from 0.015 to 250 keV in a wide range of pitch angles to determine the electron distribution function and calculate local linear growth rate as a function of frequency f and wave normal angle $\theta$. The calculations were performed for three cyclotron resonances (n = 1, 0, –1) that make the largest contributions to the wave growth rate. The calculations showed the presence of a pronounced maximum at frequencies (0.8–0.9) f_ce. The energy range and pitch angles of electrons with a maximum contribution to wave excitation at these frequencies were estimated.

1 INTRODUCTION

Cyclotron interaction between waves and particles is known to play an important role in the dynamics of the Earth’s radiation belts. Cyclotron instability regulates the fluxes of charged particles and determines their pitch-angle and energy spectra. Cyclotron instability generates whistler waves at frequencies ${{f}_{{ci}}} \ll f < {{f}_{{ce}}}$ (${{f}_{{ci}}}$ and ${{f}_{{ce}}}$ are ion and electron gyro frequencies, respectively). Unstructured broadband electromagnetic radiation in the frequency range from tens of Hz to several kHz are typical of the Earth’s inner magnetosphere (Meredith et al., 2004). The frequencies of VLF emissions generated due to cyclotron interaction of whistler waves and energetic electrons change along the satellite trajectory in proportion to the equatorial gyrofrequency (Burtis and Helliwell, 1976; Poulsen and Inan, 1988; Boskova et al., 1986). The most studied whistler mode waves in the magnetosphere are noise and chorus emissions, which are usually observed in the frequency range from 200 to 2000 Hz. Recent studies of the statistical characteristics of whistler-mode waves (Malaspina et al., 2017, 2018) have revealed low-intensity whistler waves at high frequencies up to 50 kHz in the magnetosphere (He et al., 2020; Ma et al., 2017). In recent years, new types of VLF emissions at high frequencies of 4–30 kHz have been identified at the Kannuslehto auroral station in Northern Finland (L = 5.5) using digital methods for the suppression of spherics (Manninen et al., 2016); the mechanism of generation of these VLF emissions remains unclear (Manninen et al., 2021).

Electrons with energies of 10–100 keV are believed to be most important in cyclotron resonant interaction associated with cyclotron instability related to transverse anisotropy of the distribution of energetic particles (Church and Thorne, 1983). Suprathermal electrons (~0.1–10 keV) in the inner magnetosphere also often have an anisotropic pitch-angle distribution with a maximum at 90°, which is formed due to the conservation of the first and second adiabatic invariants, when particles are transferred from the plasma layer, similar to that occurring for higher energy electrons during substorm injection (Reeves et al., 1996). The interaction of whistler waves with energetic electrons of 10–100 keV has been considered in many studies, starting with the classic papers (Andronov and Trakhtengerts, 1964; Kennel and Petschek, 1966). References to many of these studies can be found in the monograph (Trakhtengerts and Rycroft, 2011). At the same time, the role of low-energy electrons in the generation of whistler waves has not been fully studied. Maeda (1976) seem to be the first to suggest that low-energy electrons (W ~ 5 keV) could be responsible for the generation of VLF emissions observed by the Explorer 45 satellite in the evening sector during the main phase of a magnetic storm. Yahnin et al. (2019) showed that the VLF waves at frequencies 2–6 kHz observed after magnetospheric compressions can be generated due to cyclotron interaction with electrons with energy lower than 1 keV and be responsible for their precipitation. The fact that suprathermal (10–100 eV) electrons can precipitate due to efficient scattering over pitch angles during the interaction with whistler waves propagating at large angles with respect to the magnetic field was shown in (Jasna et al., 1992). He et al. (2019) believe to be the first to consider the possibility of generating high-frequency hisses by low-energy electrons—:(1–2) keV in the frequency range from 2 to 10 kHz in the plasmasphere.

This paper considers broadband electromagnetic VLF emissions recorded at 1030–1730 UT on March 17, 2019, by the Van Allen Probe-B satellite (hereafter, we will use its earlier name Radiation Belt Storm Probes (RBSP)). We analyze the spectral features of these emissions and their relationship with electron fluxes in a wide energy range from 0.015 to 250 keV. To calculate the resonant energies and local growth rates of whistler waves, which are compared with the characteristics of observed VLF waves, we use satellite measurements of differential fluxes of energetic electrons, the external magnetic field, and the cold plasma density.

2 DATA

The RBSP-A and RBSP-B satellites moved along the same highly elliptical orbit with an interval of almost 1 h. The orbital inclination of the satellites was 10°, the apogee was 5.8 Earth radii, the perigee was 700 km, and the orbital period was 9 h. The electromagnetic fields were measured on these satellites by the EMFISIS (the Electric and Magnetic Field Instrument Suite and Integrated Science) instrument (Kletzing et al., 2013) in a wide frequency range. A high-frequency receiver (HFR) recorded electric fields in the 10–5 × 10^–2 kHz band. In the ELF/VLF range, the waves were measured from 0.2 to 11 kHz using three electric and three magnetic antennas. In this paper, we analyze the spectral matrices of VLF signals calculated onboard in the surveillance mode with a time resolution of 6 s. The plasma density was determined from measured upper hybrid frequency (Kurth et al., 2015) according to the high-frequency receiver (HFR) of the EMFISIS instrument.

The RBSP satellites measured particle fluxes over a wide range of energies of 10–10⁶ eV. The Helium, Oxygen, Proton, and Electron (HOPE) mass spectrometer (Funsten et al., 2013) measured electron fluxes at 11 pitch angles from 4.5° to 175.5° in 72 energy channels with a time resolution of ~20 s. The energy range for electrons ranges from 15 keV to ~50 keV. The Magnetic Electron Ion Spectrometer (MagEIS) (Blake et al., 2013) measured particle fluxes with energies from tens of keV to several MeV with a time resolution of ~10 s. The energetic electron fluxes were measured in 23 energy channels from ~36 keV to ~4 MeV at 11 pitch angles in the range from ~8° to ~172°.

3 SPECTRAL FEATURES OF EMISSION AND THEIR RELATIONSHIP WITH LOW-ENERGY ELECTRON FLUXES

Now, we consider the features of broadband electromagnetic VLF emission spectra and their relationship with the electron fluxes measured by the RBSP-B satellite in the time interval 1030–1730 UT on March 17, 2019. This time interval was characterized by high magnetic activity, Kp = 4 in daytime hours and Kp = 3 in evening hours. The total Kp index for the previous 9 h was 14. At that time, there was a sequence of intense substorms and the AE index was approximately 500 nT (the AE index reached 1000 nT at 8–9 UT).

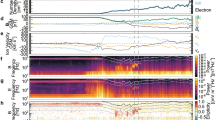
Figure 1a shows the spectra of signals recorded by the EMFISIS instrument on the RBSP-B satellite using an electric antenna in the high-frequency range. The electric and magnetic field spectra in the VLF range up to 10 kHz are shown in Figs. 1b and 1c, respectively. The black and white lines denote the electron gyrofrequency f_ce and half the gyrofrequency f_ce/2, respectively. The upper panel clearly shows the signal at the upper hybrid frequency f_UH, allowing one to determine the density of cold plasma.

Fig. 1.

The spectra of signals recorded from 1000 to 1800 UT on March 17, 2019 on the RBSP-B satellite in the frequency band 10–50 kHz on the electric antenna (a), in the frequency band up to 10 kHz on the electric (b) and magnetic (c) antennas. The black and white lines indicate the gyrofrequency of electrons f_ce and half the gyrofrequency f_ce/2, respectively.

In the time interval of interest to us (1030–1730 UT), the RBSP-B satellite was near the equatorial region at latitudes from λ = 7° to λ = –5°, moving from the daytime to the evening sector, from small L-shells (L = 3) towards large ones (L = 6) and then returning again to smaller L. Figures 1b and 1c show two pronounced bands of whistler waves: extremely low-frequency (ELF) signals predominantly below (1–3) kHz and broadband VLF signals at high frequencies, which are considered in this study. The upper frequencies of these broadband VLF emissions are less than the electron gyrofrequency f_ce and decrease as the L-shell increases. It should be noted that at frequencies higher than f_ce, various types of electrostatic emissions are observed, such as half-integer cyclotron harmonics at frequencies exceeding 3/2f_ce, intense noise emissions mainly on large L-shells in the regions of significant cold plasma variations, probably associated with cold plasma regions that have separated from the plasmasphere; these emissions are not considered here.

It can be seen from Fig. 1b that broadband emissions in the whistler mode at frequencies > f_ce/2 are recorded on the RBSP-B satellite from 1030 to 1220 UT in the daytime sector (MLT = 13–15) and from 1620 to 1730 UT in the evening (MLT = 17.7–19.5). The frequency of the upper hybrid resonance displayed in Fig. 1a shows two sharp drops at approximately 1030 UT and 1730 UT, indicating that the satellite crossed the plasmapause on L = 3.2 in the daytime sector and on L = 2.8 the evening sector. Broadband emissions were recorded immediately after the plasmapause up to L = 5.4 in the daytime sector and up to L = 4.7 in the evening sector. The upper emission frequencies reached maximum values of approximately 30 kHz near the plasmapause and decreased with increasing L-shell, remaining close to f_ce but lower by 2–5 kHz.

Let us consider the features of the VLF emission spectra recorded on the RBSP-B satellite in different orbital segments. In the daytime sector (1035–1115 UT) on L = 3.2–4.4, two maxima were regularly recorded at frequencies above and below f_ce/2; here, the amplitude of the maximum at f > f_ce/2 was always less than at f < f_ce/2. Figures 2a and 2b show examples of VLF wave spectra recorded on the electrical antenna at 1048:52 and 1108:24 UT (the electron gyrofrequency f_ce is shown by arrow). With an increase in the L-shell, the frequency of the lower maximum remained almost unchanged (3–4 kHz), while the frequency of the upper maximum f_max decreased from 12.6 kHz to 7.2 kHz; in this case, f_max = 0.78f_ce and f_max = 0.65f_ce, respectively, remaining lower than f_ce by 3.5–3.8 kHz.

Fig. 2.

The VLF emission spectra recorded on the electric antenna of the RBSP-B satellite at (a) 1048:52 UT, (b) 1108:54 UT, (c) 1639:54 UT, and (d) 1722:18 UT.

In the evening sector, noise emissions with a pronounced maximum at frequencies ~0.8f_ce were recorded from 1620 to 1655 UT on L = 4.7–4.4. An example of the electric field spectrum of this kind for 1623:12 UT is shown in Fig. 2c. As the satellite moves to smaller L-shells, the VLF emission frequencies increase and the frequency band of the observed waves expands. An example of the VLF emission spectrum for 1722:05 UT at small L-shell (L = 3) is shown in Fig. 2d. Both examples are characterized by intensity maxima with frequencies lower than  f_ce by 2 kHz (Fig. 2c) and 10 kHz (Fig. 2d).

Let us consider the relationship between VLF emissions and electron fluxes recorded on the RBSP-B satellite. Figures 3a and 3b show the spectrograms of the electric field of VLF emission in the frequency band Δ f = 10–35 kHz and the magnetic field in the band Δ f = 2–11 kHz, respectively. The horizontal lines show the time intervals for detecting emission at frequencies  f  > f_ce/2 on the RBSP-B satellite. The bottom panels of Fig. 3c and 3d show differential electron fluxes for a pitch angle of 90°, measured by the HOPE instrument in the energy range 0.1–30 keV. It can be seen that the VLF emissions at frequencies exceeding f_ce/2 are associated with the intensification of low-energy electron fluxes with W > 10² eV (Fig. 3c). Figure 3d shows the pitch-angle distributions of differential electron fluxes for energy 525.8 eV. It can be seen from Fig. 3d that the low-energy electrons that correlate with high-frequency VLF waves have a transverse anisotropy favorable for the development of cyclotron instability.

Fig. 3.

The relationship between VLF emission and electron fluxes recorded on the RBSP-B satellite. Spectra of signals recorded with (a) an electric antenna in the frequency band 10–35 kHz and (b) a magnetic antenna in the frequency band 2–11 kHz. (c) Electron fluxes for a pitch angle of 90°, measured by the HOPE instrument in the energy range 0.1–20 keV. (d) Pitch-angle distributions of differential electron fluxes for an energy of 525.8 eV.

4 CALCULATIONS OF WHISTLE WAVE GROWTH RATES FROM MEASUREMENTS OF ELECTRON FLUXES

To explain the features of the spectrum of whistler waves described in the previous section, we calculated the linear growth rate using measurements of energetic particle fluxes onboard the RBSP-B satellite. We assume that these waves are generated in the equatorial region of the magnetosphere near the observation point, so that the features of the observed spectrum can be understood from the local growth rate analysis. Below, we will see that the maximum growth rate for the experimentally determined distribution function corresponds to purely longitudinal propagation, when waves are excited only at the first cyclotron resonance. However, during the propagation of waves with frequencies above half the electron gyrofrequency, the angle of the wave normal changes rather quickly, so that the growth rate is contributed by, generally speaking, all cyclotron resonances, primarily, the resonances n = 1, 0, –1, corresponding to the lowest values of the resonance energy and taken into account by us in the calculations.

The linear growth rate of a whistler wave propagating at an angle θ to the external magnetic field has the form (Shklyar and Matsumoto, 2009):

$$\begin{gathered} {{\gamma }_{{L~}}} = \frac{{{{{(\pi e\left| E \right|)}}^{2}}{{\omega }_{{ce}}}}}{{2m{{k}_{\parallel }}U}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} - \infty }^\infty {\int\limits_0^\infty {{{I}_{n}}d\mu ,} } \\ {{I}_{n}} = V_{n}^{2}\left( \mu \right){{\left( {\frac{{\partial {{f}_{0}}}}{{\partial w}} + \frac{n}{\omega }\frac{{\partial {{f}_{0}}}}{{\partial \mu }}} \right)}_{{w{\kern 1pt} = {\kern 1pt} {{mv_{{Rn~}}^{2}} \mathord{\left/ {\vphantom {{mv_{{Rn~}}^{2}} 2}} \right. \kern-0em} 2}{\kern 1pt} + {\kern 1pt} \mu {{\omega }_{{ce}}}}}}. \\ \end{gathered} $$

(1)

Here, e and m are the electron charge and mass, respectively, ${{\omega }_{{ce}}} = 2\pi {{f}_{{ce}}}$ is the absolute value of the cyclic electron gyrofrequency, ${{k}_{\parallel }}$ is the longitudinal component of the wave vector, $\left| E \right|$ is the amplitude of the perpendicular component of the electric field of the wave in the plane formed by the external magnetic field B₀ and the wave vector k, and U is the wave energy density:

$$U = \frac{1}{{16\pi \omega }}\frac{\partial }{{\partial \omega }}\left( {{{\omega }^{2}}{{\varepsilon }_{{\alpha \beta }}}} \right)a_{\alpha }^{{\text{*}}}{{a}_{\beta }}{{\left| E \right|}^{2}},$$

(2)

where ${{\varepsilon }_{{\alpha \beta }}}$ is the dielectric permittivity tensor, ${{a}_{\alpha }},{{a}_{\beta }}$ are the polarization coefficients, and “*” means complex conjugation. In the local coordinate system $\left( {x,y,z} \right)$, where the external magnetic field is directed along the z-axis and the wave vector lies in the $\left( {x,z} \right)$-plane, the dielectric permittivity tensor and polarization coefficients have the following form (${{\omega }_{p}}$ is the electron plasma frequency and c is the speed of light):

$${{\varepsilon }_{{\alpha \beta }}}\left( \omega \right) = \left( {\begin{array}{*{20}{l}} {{{\varepsilon }_{1}}}&{i{{\varepsilon }_{2}}}&0 \\ { - i{{\varepsilon }_{2}}}&{{{\varepsilon }_{1}}}&0 \\ 0&0&{{{\varepsilon }_{3}}} \end{array}} \right),$$

(3)

where the real values ${{\varepsilon }_{1}},~{{\varepsilon }_{2}},$ and ${{\varepsilon }_{3}}$ are

$${{\varepsilon }_{1}} = 1 - \frac{{\omega _{p}^{2}}}{{{{\omega }^{2}} - \omega _{{ce}}^{2}}},\,\,\,\,~{{\varepsilon }_{2}} = \frac{{\omega _{p}^{2}{{\omega }_{{ce}}}}}{{\omega {\kern 1pt} ({{\omega }^{2}} - \omega _{{ce}}^{2})}},\,\,\,\,{{\varepsilon }_{3}} = 1 - \frac{{\omega _{p}^{2}}}{{{{\omega }^{2}}}},$$

and

$${{a}_{y}} = - i\frac{{\frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{2}}}}{{{{k}^{2}} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{1}}}}{{a}_{x}},\,\,\,\,~{{a}_{z}} = \frac{{{{k}_{x}}{{k}_{z}}}}{{k_{x}^{2} - \frac{{{{\omega }^{2}}}}{{{{c}^{2}}}}{{\varepsilon }_{3}}}}{{a}_{x}}.$$

(4)

The coefficients of the dielectric permittivity tensor are written disregarding ions and can be applied to whistler waves with frequencies above the lower hybrid resonance frequency. In our coordinate system, the value of |E| is equal to the magnitude of the x-component of the electric field of the wave. Without loss of generality, the polarization coefficient a_x can be taken to be unity, which only changes the value of |E|.

Now, we further explain the notations used in the expression for the linear growth rate (1). We note that the unperturbed distribution function in (1) is considered to be a function of particle kinetic energy $w = {{m{{v}^{2}}} \mathord{\left/ {\vphantom {{m{{v}^{2}}} 2}} \right. \kern-0em} 2}$ and magnetic moment $\mu = {{mv_{ \bot }^{2}} \mathord{\left/ {\vphantom {{mv_{ \bot }^{2}} {2{{\omega }_{{ce}}}}}} \right. \kern-0em} {2{{\omega }_{{ce}}}}}$. Being integrals of particle motion in the absence of a wave, these quantities are natural variables for the unperturbed distribution function. ${{v}_{{Rn~}}}$ is the resonant velocity corresponding to the nth cyclotron resonance

$${{v}_{{Rn~}}} = \frac{{\omega - n{{\omega }_{{ce}}}}}{{{{k}_{\parallel }}}}$$

(5)

and the coefficient V_n, which has the meaning of the amplitude of the resonant interaction of the wave with particles at the nth cyclotron resonance, is expressed as

$$\begin{gathered} {{V}_{n}}\left( \mu \right) = \left( {\frac{{n{{\omega }_{{ce}}}}}{{{{k}_{ \bot }}}}{{a}_{x}} + {{v}_{{Rn~}}}{{a}_{z}}} \right){{J}_{n}}\left( \rho \right) - \frac{{i\rho {{\omega }_{{ce}}}}}{{{{k}_{ \bot }}}}{{a}_{y}}J_{n}^{'}\left( \rho \right), \\ ~\rho = {{k}_{ \bot }}{{\left( {\frac{{2\mu }}{{m{{\omega }_{{ce}}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $$

(6)

where ${{J}_{n}}\left( \rho \right)$ and $J_{n}^{'}\left( \rho \right)$ are the nth order Bessel function of the first kind and its derivative with respect to the argument ρ. It follows from expression (5) for the resonant velocity that the resonances n = 1, n = 0, and n = –1 correspond to the smallest absolute values of the resonant velocity; for n = 1, the resonant velocity is negative.

Now, we turn to the expression for the electron distribution function f₀ in terms of the experimentally measured differential particle fluxes. This is a well known expression, and its detailed derivation can be found, for example, in (Shklyar et al., 2020). The experimentally measured differential particle flux as a function of energy w and pitch angle α is usually expressed in practical units of 1/(cm² s sr keV), and the energy is expressed in keV. In this case, the particle distribution function in the CGS system is expressed as

$$f\left( {w,\alpha } \right) = 1.62 \times {{10}^{{ - 37}}}\frac{J}{W}~{\kern 1pt} ,$$

(7)

where J is the differential electron flux in the units indicated above and W is the electron energy in keV. Since the measured differential flux depends on energy w and pitch angle α, distribution (7) turns out to be a function of the same variables. Clearly, the distribution function can be expressed in terms of any variables that uniquely determine the particle energy and pitch angle. Below, we use the variables w and μ, which express growth rate (1). In this regard, we make two remarks. First, the magnetic moment, energy, and pitch angle are related as $\mu {{\omega }_{{ce}}} = w{\text{si}}{{{\text{n}}}^{2}}\alpha$; therefore, it is also necessary to know the sign of sin α, in addition to the energy and magnetic moment, to determine the pitch angle. This is related to the fact that if the distribution function is not symmetric with respect to the pitch angle of 90°, then the growth rates of same-frequency waves and same |cos θ| turn out to be different (Shklyar et al., 2020). Second, it should be emphasized that the distribution function is always normalized so that $\int {fd{\mathbf{v}} = n\left( {\mathbf{r}} \right)} ,$ where n(r) it is the local density of particles, whatever the variables of the distribution function. Formulas (7) and (1) make it possible to calculate numerically the wave growth rates from measured differential particle fluxes.

It is known that the growth rate and resonance interaction of waves and particles are largely determined by the resonant velocity, which specifies the minimum energy of particles interacting with the wave on the nth cyclotron resonance

$${{w}_{{{\text{min}}{\kern 1pt} {\kern 1pt} ~n}}} = {{w}_{{||Rn~}}} \equiv \frac{{mv_{{~Rn~}}^{2}}}{2}~.$$

(8)

Hereafter, for quantities related to the first cyclotron resonance, the subscript “n” is omitted. Since the maximum frequency for whistler waves is the electron gyrofrequency, we present the quantities as function of frequency in the range of up to the electron gyrofrequency.

Figures 4a and 4b show the dependence of the longitudinal resonant energy ${{w}_{{||R~}}}$ and plasma density along the RBSP-B orbit on March 17, 2019 for the case of longitudinal propagation, when the resonant energy is a single-valued function of relative frequency and parameters of the surrounding plasma. The values of the longitudinal resonance energy ${{W}_{{||R}}}$ at the first cyclotron resonance (the only one that exists in the case of longitudinal propagation) are given for four values of the relative frequency f/f_ce = 0.5, 0.6, 0.7, 0.8. It is important that the resonant energies are in the range ${{W}_{{||R}}} = \left( {500{\kern 1pt} - {\kern 1pt} 100} \right)~$ eV for waves with frequencies near the gyrofrequency f = (0.7–0.8)f_ce. It can also be seen from Fig. 4 that the resonant energies of whistler waves anticorrelate with plasma density during its rapid changes in the region of the plasmapause and plasma inhomogeneities from 1250 to 1620 UT. Since the measurements of the external magnetic field and plasma density are available with different time resolutions, we interpolated the density and magnetic field to a common time scale to plot the dependences shown in Figs. 4.

Fig. 4.

(a) The parallel resonant energy along the satellite trajectory for four relative frequencies. (b) Cold plasma density measured onboard the RBSP-B satellite.

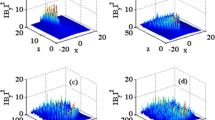
Figure 5 shows the local amplification factor γ_L as a function of frequency and propagation angle, taking three cyclotron resonances into account, for 1644:48 UT when the satellite was at the latitude of λ = –2.2° on L = 4.1.

Fig. 5.

The local increment of whistler waves, normalized to the electron gyrofrequency ω_ce, as a function of frequency and propagation angle for March 17, 2019, at 1644:48 UT. At this time instant, ω_ce = 7.57 × 10⁴ s^–1.

In this case, the local gyrofrequency was 12.04 kHz. As mentioned above, when the distribution function is asymmetric with respect to the pitch angle of 90°, the growth rates of the waves propagating in different directions relative to the external magnetic field are not equal. For definiteness, we consider waves propagating from south to north, i.e., in a positive direction with respect to the external magnetic field. It can be seen from the figure that the growth rate has a local maximum at the propagation angle θ = 0 for all frequencies and small propagation angles. However, this is not an absolute maximum for all frequencies: for some frequencies, the growth rate maximum corresponds to the propagation angles near the resonant cone, i.e., $\theta = ~\arccos ~\left( {{\omega \mathord{\left/ {\vphantom {\omega {{{\omega }_{{ce}}}}}} \right. \kern-0em} {{{\omega }_{{ce}}}}}} \right)$. As an example, the growth rate maximum near the resonant cone at 1644:48 UT was in the range of frequencies 8–10 kHz and angles θ = 35°–50°.

It is known that the emissions generated near the resonant cone are quasi-electrostatic, while the emission we discuss is electromagnetic; therefore, we disregard the generation of waves near the resonant cone. Since the growth rate is maximal at θ = 0, we consider the growth rate as a function of frequency for zero propagation angles θ. This dependence is shown in Fig. 6a. An important feature of the growth rate is that there are two maxima at frequencies below and above half the gyrofrequency. The VLF spectrum on the RBSB-B satellite for this time is shown in Fig. 6b. Comparing Fig. 6a and Fig. 6b, one can see that the observed emission spectrum also has two maxima, the lower of which in the 4–6 kHz band is sufficiently close in terms of frequency to the calculated value, and the upper lies at a frequency that differs from (is lower than) the frequency of the second maximum of the calculated growth rate by almost 2 kHz.

Fig. 6.

(a) The local increment as a function of frequency for propagation angle θ = 0, (b) spectrum of VLF waves recorded by the electric antenna on the RBSP-B satellite at 1644:48 UT, (c) local increment as a function of frequency for propagation angle θ = 0 for only high energies (MAGEIS instrument), and (d) local increment as a function of frequency for propagation angle θ = 0 for only low-energy particles (HOPE instrument).

A natural question arises about energies and pitch angles of the particles that are responsible for the respective growth rate maxima. To answer this question, we calculated the growth rate as a function of frequency, taking into account only high-energy particles with energies from 32 to 604 keV (their fluxes were measured by the MagEIS instrument (Fig. 6c)) and only low-energy particles with energies from 0.015 upto 29.168 keV (their fluxes were measured by the HOPE instrument (Fig. 6d)). It follows from a comparison between Figs. 6a, 6c, and 6d that high-energy particles are mainly responsible for the low-frequency maximum, although low-energy particles also make a significant contribution; the high-frequency maximum of the growth rate is associated with low-energy particles.

To determine the particle energies and pitch angles that make the main contribution to the growth rate at a given frequency, we present (see Figs. 7 and 8) the quantities proportional to the integrand I₁ in formula (1) for two frequencies corresponding to the low-frequency (Fig. 7) and high-frequency (Fig. 8) growth rate maxima. I₁ corresponds to the contribution of the first cyclotron resonance to the growth rate. The function shown in the figure is normalized to the maximum absolute value I_1max. The integrands are given as functions of energy (the top panels of the figures) and pitch angles (the bottom panels of the figures). For the given frequency and local plasma parameters, the longitudinal resonant velocity and, consequently, the longitudinal energy of resonant particles are fixed; therefore, the pitch angle is uniquely related to the particle energy. Accordingly, the bottom panels, which do not carry fundamentally new information, are given only for clarity. It can be seen from Fig. 7 that particles with energies of 30–90 keV and pitch angles of 109°–115° make the maximum contribution to the excitation of the low-frequency maximum of whistler waves at a frequency of 5.1 kHz. Particles with energies of 0.5–3 keV and pitch angles of 97°‒120° make the maximum contribution to the excitation of the high-frequency maximum of whistler waves at a frequency of 10.1 kHz (0.85 f_ce) (Fig. 8).

Fig. 7.

The normalized value of I₁ [see (1)] determining the contribution to the increment of high-energy particles interacting with a 5.1-kHz wave at the first cyclotron resonance, as a function of particle energy (top panel) and as a function of pitch angle (bottom panel).

Fig. 8.

The normalized value [see (1)] determining the contribution to the increment of low-energy particles interacting with a 10.1-kHz wave at the first cyclotron resonance as a function of particle energy (top panel) and as a function of pitch angle (bottom panel).

5 COMPARISON OF THE SPECTRA OF OBSERVED VLF WAVES WITH CALCULATED LOCAL GROWTH RATES OF WHISTLER WAVES

Let us consider other examples when the spectra of observed VLF emission are compared with calculated growth rates. Figure 9 shows a VLF emission spectrum typical of the daytime sector recorded by the electric antenna on the RBSP-B satellite at 1108 UT (Fig. 9a) and the growth rate of a whistler wave calculated for the wave normal angle θ = 0 based on the data from MagEIS and HOPE instruments (Fig. 9b). Both the spectrum of VLF waves and calculated data have a pronounced maximum at low frequencies < f_ce/2 close to 3 kHz. At high frequencies, the VLF emission spectrum also has a maximum at a frequency of about 7 kHz, after which the intensity of waves on the satellite decreases sharply. The calculated growth rates also have a pronounced maximum at high frequencies approximately 0.8 f_ce = 9 kHz; however, the frequency of this maximum exceeds the experimental value by 2 kHz.

Fig. 9.

Comparison of the spectra of VLF waves recorded on the electric antenna on the RBSP-B satellite at (a) 1108:54 UT, (c) 1623:37 UT, and (e) 1657:39 UT with calculated increments of local whistler waves (b, d, f).

In the evening sector, the VLF emission spectra at 1620‒1730 UT changed significantly. At 1620 UT, VLF noise emissions appear on the RBSP-B satellite with a pronounced maximum at frequencies above f_ce/2 and at 1623:37 at f_max = 6.3 kHz ≈ 0.75 f_ce (see Fig. 9c). The corresponding growth rate for θ = 0 is shown in Fig. 9d, which also demonstrates a pronounced maximum at f_max = 7.5 kHz ≈0.9 f_ce, but located approximately 1 kHz higher in frequency than in the emission spectra observed on the RBSP B satellite. The growth rate calculations also show the presence of a low-frequency maximum at 3.5 kHz, which is not detected on the satellite at 1623:37 UT (see Fig. 9c). The absence of this low-frequency maximum in the emissions may be associated, for example, with a smaller growth rate (γ_max ≈ 20 s^–1) as compared to the high-frequency maximum (γ_max ≈ 30 s^–1) and/or to the specific features of whistler wave reflection in the lower ionosphere, which cannot be controlled in this experiment. After 1630 UT, the lower frequencies f ~ 3–5 kHz in VLF emissions become more pronounced, and two maxima are observed in the emission spectrum (see Fig. 6b); here, the low-frequency maximum at approximately 5 kHz is in good agreement with the calculated growth rate (see Fig. 6a) and the frequency of the second high-frequency maximum at approximately 9 kHz was also lower than the maximum in the growth rate by 2 kHz (see Fig. 6a).

When the satellite moves further to lower L shells, the emission band at low frequencies expands shifting towards higher frequencies and both maxima merge; an example of this spectrum is shown in Fig. 9d for 1657 UT. The corresponding growth rate for θ = 0 is shown in Fig. 9f. It can be seen from Fig. 9e that VLF emissions were observed on the satellite at frequencies above 4 kHz, reached a maximum intensity at frequencies of 10–12 kHz; the wave amplitude then sharply decreased. The calculated growth rate of whistler waves (Fig. 9f) behaves similarly at low frequencies, gradually increasing and reaching a maximum at approximately 11 kHz; however, at high frequencies, an additional maximum is observed at a frequency of 13.5 kHz, which exceeds the intensity maximum by 1.5 kHz in the spectra of whistler waves observed on the satellite. It should also be noted that in the evening sector, when the satellite moves to lower latitudes, the intensity of VLF waves on the satellite and the growth rates of whistler waves simultaneously increase, and the frequency range of the observed waves and positive growth rates expands to high frequencies.

Thus, a comparison of calculated local growth rates of whistler waves and observed spectra of VLF emissions onboard the RBSP-B satellite in the given examples (Figs. 6a and 6b; Fig. 9) shows good agreement between the VLF spectra and the frequency–amplitude characteristics of the positive growth rate of whistler waves, except for the high-frequency region close to f_ce, where VLF emissions are not recorded; the maximum upper frequencies in emission spectra are f ≈ (0.65‒0.8) f_ce.

6 DISCUSSION AND CONCLUSIONS

The frequencies of broadband VLF emissions recorded onboard the RBSP-B satellite on March 17, 2019 show a dependence on the electron gyrofrequency f_ce, decreasing as the satellite moves towards large L-shells (Fig. 1). This indicates that the observed emissions are generated by the cyclotron interaction of electrons with whistler waves, which is most effective near the equator, where the RBSP-B satellite was located during the event. Therefore, we assume that the observed VLF emissions are generated in the equatorial region of the magnetosphere near the observation point. Then, the features of the observed spectrum of VLF waves can be understood from the analysis of the local growth rate calculated from electron fluxes measured on the RBSP-B satellite. Since the observed VLF emissions had small angles of the wave normal, we compared their spectra with the local growth rates of whistler waves for θ = 0, at which the growth rate is maximum.

The frequency band with positive wave growth rates decreased with increasing L and generally corresponded to the frequency band of observed broadband VLF emissions. In addition, the growth rate has characteristic features that were present in the spectra of recorded emissions. For example, both in observations and in calculations, two maxima (below and above half the gyrofrequency) are often present. A characteristic feature of the calculated growth rates of whistler waves is the high-frequency maximum at f = (0.8–0.9) f_ce. However, the spectra of the observed VLF emissions were characterized by high-frequency maxima recorded at slightly lower (by ~ 1 – 2 kHz) frequencies (see Figs. 6 and 9). We believe that this is associated with the specific features of whistler wave propagation near the gyrofrequency in the equatorial region. Figure 10a shows the trajectory of a whistler wave starting at the equator on L = 4 with θ = 0 and frequency f = 0.9 f_ce at the starting point. Figure 10b shows the wave normal angle and relative frequency f/f_ce as functions of latitude along the wave trajectory; this trajectory corresponds to a propagation time of 1 s. It can be seen from Fig. 10 that the wave significantly deviates from the starting field line, the wave normal angle increases, approaching the angle of the resonant cone, and the relative frequency of the wave decreases. Therefore, the intensity maximum of the emission observed on the satellite outside the equator should have lower relative frequencies than the relative frequencies of the maximum calculated growth rate in the generation region.

Fig. 10.

(a) The trajectory of a whistler wave starting at the equator on L = 4 with wave normal angle θ = 0 and frequency f = 0.9 f_ce at the starting point. (b) Wave normal angle and (c) relative frequency f/f_ce as a function of latitude along the trajectory.

Let us analyze the link between the VLF emissions observed on the RBSP-B satellite and on the ground. It can be seen from Fig. 1 that the emissions at frequencies below half the gyrofrequency in the daytime sector are much more intense than in the evening sector. This is consistent with the calculated wave growth rates, which are significantly larger in the daytime sector for f < f_ce/2 than in the evening sector. In the presence of ducts, the waves with these frequencies can reach the ground (Helliwell, 1965); therefore, these emissions can be expected to be observed on the ground primarily in the daytime sector. This assumption is confirmed by the analysis of VLF data obtained at the ground-based Kannuslehto station (L = 5.5), where no VLF emissions were observed in the evening sector, and quasi-periodic VLF emissions were recorded in the morning sector, having a spectral–temporal structure similar to that observed simultaneously on the RBSP-B satellite.

In conclusion, we formulate the main results of this study.

The spectral characteristics of broadband VLF emissions and their link to differential electron fluxes in a wide energy range were analyzed. Calculations of local growth rates of whistler waves were performed using the measured electron distribution function, with the account of three cyclotron resonances. The calculated growth rates and observed spectra of VLF waves often contain two maxima at frequencies below and above f_ce/2.

It follows from these results that relatively low-energy electrons (W does not exceed approximately 3 keV) are responsible for the generation of the high-frequency band of VLF emissions (f > f_ce/2); here, the excitation of these waves is associated with transverse anisotropy in the electron velocity distribution. The role of low-energy electrons in the generation of high-frequency plasmaspheric hisses at frequencies f < f_ce/2 was discussed in (He et al., 2019). Concerning the emissions outside the plasmasphere, our calculations revealed that emissions at frequencies f < f_ce/2 are excited by high-energy electrons with energies above 30 keV.

We found that the comparison between the observed high-frequency spectrum and wave growth rates calculated from local measurements outside the equator should take the fact into account that the wave propagation starting at the equator with θ = 0 at frequencies f > f_ce/2 is accompanied by a persistent reduction of their L-shells and a relevant reduction of their relative frequency. Therefore, the relative frequency of the maximum intensity of the observed spectrum turns out to be lower than the relative frequency of the growth rate maximum under the assumption that the distribution functions in the generation region and in the region of observed waves are similar.