1 INTRODUCTION

The different methods used to study the upper atmosphere and the ionosphere reveal mutually consistent changes in these geospheres during the period of the preparation of earthquakes of different classes (Nasyrov, 1978; Liperovskii et al., 1992; Rulenko, 2000; Ondoh, 2000, 2009; Silina et al., 2001; Hobara and Parrot, 2002; Pulinets and Boyarchuk, 2004; Ouzounov and Freund, 2004; Korsunova and Khegai, 2006; Liu et al., 2006; Korsunova and Khegai, 2014; Bychkov et al., 2017). These changes may be precursors of impending earthquakes, since they correspond in place and time of occurrence to the known precursor effects in the ground geophysical fields (monographs by Sidorin (1992) and Pulinets et al. (2014)).

Among the possible ionospheric earthquake precursors (IEPs), deviations of the critical frequency of the regular F2 layer (foF2), the limiting frequency and the screening frequency of the sporadic Е layer (foEs, fbEs), and its virtual heights (h'Es) from the median values during the period of the preparation of strong earthquakes with М ≥ 6.0 have been studied quite well in the last decade (Korsunova and Khegai, 2006, 2014; Perrone et al., 2010). The changes in these parameters were obtained via long-term observations at ground stations of ionospheric vertical sounding (GSIVS); they make it possible to assess the state of the upper (F region) and lower (Е region) ionosphere before the earthquakes.

Other methods have also been developed to study the ionosphere: in situ satellite (Parrot et al., 2006; Sarkar et al., 2007) and GPS measurements (Saroso et al., 2008; Xia et al., 2011). The unquestionable merit and advantage of these measurement methods are their globality and highest discreteness in time, which made it possible to refine the spatial scales of the impending powerful earthquakes. These methods can be used to obtain sufficiently full information on the changes in the upper ionosphere, while the data on the state of the lower ionosphere are much more limited. Therefore, measurements of the sporadic Е layer parameters at GSIVS is still relevant.

As early as the 1990s, significant changes in the Еs were recorded before strong earthquakes: an increase in the probability of occurrence and frequencies and a decrease in layer semitransparency, as indicated in studies (Alimov et al., 1989; Liperovskaya et al., 1994; Ondoh, 2000). It was shown (Silina et al., 2001) based on the study of 25 Central Asian earthquakes with magnitudes of М ≥ 5.5 that the nighttime mean values of screening frequencies decrease 1–2 days before the main shock and the layer semitransparency, which decreases prior to the earthquake moment, increases three days before the shock. The similar results were also obtained for the diurnal mean values of the semitransparency coefficient of the Еs layer according to the measurement data in Japan, as noted in a monograph (Pulinets et al., 2014). In addition, detailed studies were performed for changes not only in the frequency parameters of Еs but also in its virtual heights, which made it possible to detect significant changes in these parameters during the preparation of earthquakes with М ≥ 6.0 (Korsunova and Khegai, 2006, 2014).

All of these results were obtained in the epignosis and were tied to the dates of events that had already happened. It is unclear how an impending earthquake can be predicted in real time based on data on its ionospheric precursors, including changes in Еs. Significant deviations in the ionospheric parameters can be determined by some other different geophysical processes that are not related to earthquakes. For example, it was shown (Perrone et al., 2010) that significant changes in ionospheric parameters that are similar to precursor effects were also recorded in the absence of earthquakes in about 50% of cases. Nevertheless, according to the Hanssen–Kuipers Score or Rscore (True Skill Statistic, Pierce Skill Score (Chen et al., 2004)), the effectiveness of the detection of possible IEPs (Korsunova and Khegai, 2015) under quiet geomagnetic conditions is rather high for a swarm of 34 Kamchatka earthquakes with М = 4.6–6.0, since the Rscore is 0.82. This value represents the difference between the probability of the detection of a true earthquake precursor and the probability of the detection of a “false” precursor. The change in this value ranges from –1 to 1, where the latter indicates 100% probability of the detection of a true precursor in the absence of “false” alarms.

Another uncertainty is related to the prediction of the main shock time based on data on the lead time of the occurrence of an ionospheric earthquake precursor. Studies (Korsunova and Khegai, 2006; Korsunova and Khegai, 2018) showed that IEPs can be both middle- or short-term in full conformity with the known data from ground measurements (Zubkov, 1987). Therefore, we need criteria to identify precisely short-term ionospheric earthquake precursors (STIEPs) that predict the earthquake moment by hours or days, which is extremely important for earthquake-prone regions. These criteria were determined (Korsunova and Khegai, 2018) from an analysis of data from long-term observations at the GSIVS chain in Japan for 30 strong earthquakes with М ≥ 6.5.

These criteria were obtained based on an analysis of hourly measurements of four ionospheric parameters, h'Es, foEs, fbEs, and foF2, during simultaneous measurements at spaced GSIVIS in the preparation period of a series of earthquakes. It turned out that only short-term precursors are characterized by (a) the appearance of maximum deviations in all studied parameters on the same and (b) deviations that are observed at stations located in the preparation zone of a particular earthquake but are located several hundred kilometers from each other. However, during the automatic processing of ionograms, modern digital ionosondes record only the main sporadic formation, although, in fact, several layers may occur at different heights. All types of sporadic formations in the Е region, including high layers (which occur quite infrequently), are identified during the manual processing of ionograms. It is very important to calculate the height h'Es of the sporadic Е layer, since its maximum deviations were used to estimate the lead-time of the earthquake moment ΔТh'Es based on a possible short-term IEP (Korsunova and Khegai, 2018). Conversely, the foEs value is fixed quite reliably with any method of ionogram processing and is always present in observation tables if a sporadic E layer exists at the particular hour of the day; therefore, at the assigned time interval of days, the probability of its occurrence PEsi on each day i can be determined (here, subscript i is the sequence number of the day at the selected continuous time interval of days). It is unknown in advance whether any diurnal characteristics related to foEs and PEsi can meet the criteria for the detection of short-term IEPs. An answer to this question requires comparison of the results of the detection of possible short-term IEPs based on the entered diurnal characteristics of Es to IEPs detected earlier (Korsunova and Khegai, 2018) based on hourly measurements of all Еs parameters for the same earthquakes.

Therefore, the purpose of our study is to analyze the changes in diurnal characteristics δPEs and ΔfEsΣ that we introduced, as determined below, before the strong earthquakes with М ≥ 6.5 according to data from simultaneous measurements at GSIVS located several hundred kilometers from each other that were already been examined (Korsunova and Khegai, 2018). Such an analysis will make it possible to assess the effectiveness of the use of these Еs characteristics to identify short-term ionospheric precursors of impending earthquakes in terms of the procedure of their detection.

2 DATA ANALYSIS AND RESULTS

We considered the measurement data on the limiting frequency of reflection from the Еs layer obtained via manual and automatic ionogram processing at several spaced GSIVS within the preparation zone of a given earthquake. The observation results at the following four stations for 1972–2004 were used: WAKKANAI (geographical coordinates: φ = 45.2° N, λ = 141.8° E), KOKUBUNJI (geographical coordinates: φ = 35.7° N, λ = 139.5° E), AKITA (geographical coordinates: φ = 39.7° N, λ = 140.1° E), and YAMAGAWA (geographical coordinates: φ = 31.2° N, λ = 130.5° E). The considered 19 earthquakes with М = 6.5–7.4 were taken from the group for which possible shorts-term IEPs were identified earlier (Korsunova and Khegai, 2018) based on hourly measurements of four ionospheric parameters: h'Es, foEs, fbEs, and foF2.

A precondition for the selection of earthquakes by Korsunova and Khegai (2018) was the absence of strong geomagnetic perturbations during the preparation period with a planetary index of Kp ≤ 30. The hourly ionospheric data for the four-day preparation time, including the day of the earthquake, were analyzed. The integral diurnal Es characteristics were used in this work to identify possible earthquake precursors. Therefore, taking into account the sporadic character of Es occurrence, we increase the length of the analyzed periods of earthquake preparation to 10 days. Such an increased time interval often shows significant geomagnetic perturbations; therefore, we select those earthquakes that had no geomagnetic perturbations with Kp ≥ 40 during most of the preparation time. It was found that 20 earthquakes had М = 6.5–7.4.

The stations for each earthquake were based on the STIEP identification criterion, which is characterized by the simultaneous appearance of anomalous deviations in the ionospheric parameters at GSIVS located hundreds of kilometers apart that fall within the preparation zone of a particular earthquake.

The best known and well-established estimation of the radius of the zone of earthquake preparation on the Earth’s surface relative to its epicenter (with respect to M) is the theoretical estimation made by Dobrovolsky et al. (1979). According to this estimation, this radius (ρD, km) is calculated with the expression ρD = 100.43M, and it implies that the depth of the earthquake hypocenter tends to zero. However, as noted in the monograph (Sidorin, 1992), first, analysis of the experimental data shows that there are quite a number of examples of the observation of earthquake precursors at a much greater distance from the earthquake epicenters. Second, much better results are yielded via estimation of the sizes of the zones of the manifestation of earthquake precursors in solid Earth, which was obtained by the author and his colleagues based on an analysis of experimental data on deformation precursors at the same threshold level of their detection as that given by Dobrovolsky et al. (1979). According to this estimation, the radius of the zone of the manifestation of possible earthquake precursors (ρS, km) can be represented by the formula ρS = 100.48M. In this respect, this dependence much better agrees with the experimental data on the northwestern part of the Pacific seismic belt than others. Our work addresses the earthquakes of this region. Moreover, it turns out (the monograph by Aprodov (2000)) that the deeper the earthquake source is, the greater is the territory covered by seismic manifestations at an equal earthquake energy.

Hence, we take the condition Re ≤ ρS as the principal criterion of earthquake selection for the analysis (here, Re is the great-circle distance from the epicenters to GSIVS, in km). It is known that all stations except for AKITA are spaced at distances exceeding 900 km; therefore, Re > ρD for some of the selected earthquakes. The observations at AKITA were terminated in 1993; therefore, for earthquakes occurring after that year, one station more often fell into the preparation zone according to Dobrovolsky (Re ≤ ρD), while the others were outside this zone. Hence, the ionospheric data for each selected earthquake were analyzed for the two distant stations with the closest epicentral distances, at least one of which was in the preparation zone of a particular earthquake according to Dobrovolsky. As a result, one of 20 earthquakes was excluded, since both stations were outside the zone of earthquake preparation according to Dobrovolsky.

Precursor effects are usually detected in the ionosphere based on an analysis of deviations of particular parameters from the median or mean values for a certain period of time. In our case, we consider the deviations of two parameters, PEs and foEs, from the medians for 10 days before each earthquake and on the day of the earthquake itself for the selected pairs of GSIVS within the preparation zone of a given earthquake. At the first stage, according to tabular data of hourly foEs measurements, we calculated PEsi = NEsi/ni, where NEsi is the number of Es occurrences on the particular day, ni is the number of measurements actually performed on that day; 1 ≤ ni ≤ 24, and i ∈ [–10, 0]. To compare data from the different stations, where Es may form under different geophysical conditions, we determine the deviations of the actual PEsi from their median values for each earthquake over an 11-day period: δPEsi = PEsi – PEsmed.

The algorithm for the calculation of foEs deviations differs from that described above, since it was necessary to eliminate the local time dependence of foEs in further consideration of the data from the different stations. Therefore, first, for each hour of a day (subscript j), we found the median of distribution fmedEsj for the study period of time of 11 days and then the deviations of particular hourly values from it: Δj fEs = foEsj – fomedEsj (subscript j ∈[0, 23]) if there is a value of  foEsj and fomedEsj for a given hour of a particular day. When the value of foEsj and/or fomedEsj is absent for a given hour of the day, Δj fEs remains undetermined and this difference was not taken into account in the calculation of the total (integral) weighted diurnal deviation. Then, for each day, we calculated the weighted mean (total) integral diurnal deviations ΔfEsΣ with the formula

$$\Delta {\kern 1pt} fE{{s}_{\Sigma }} = {{[{{\Delta }_{1}}fEs + {{\Delta }_{2}}fEs + \ldots + {{\Delta }_{{23}}}fEs]} \mathord{\left/ {\vphantom {{[{{\Delta }_{1}}fEs + {{\Delta }_{2}}fEs + \ldots + {{\Delta }_{{23}}}fEs]} {{{n}_{i}},}}} \right. \kern-0em} {{{n}_{i}},}}$$
(2)

where ni is the number of Δj fEs values considered in each particular day i.

Figure 1 presents an example of changes in the indicated values of δPEsi (in percent) and ΔfEsΣ for the earthquake of October 31, 2003, with М = 7.0. Each point on the plots corresponds to the parameter value on a particular day counted from the day of earthquake (0 day) per Japan standard time JST = UT + 9 h. The arrow shows the day of the earthquake, and the shaded ellipsis designates the maxima in the changes in the deviations of the considered parameters observed on the same day for both parameters at two distant GSIVS.

Fig. 1.
figure 1

Changes in the diurnal parameters for δРЕs (left ordinate axis, solid lines) and ΔfEsΣ (right ordinate axis, dash-and-dot lines) at an 11-day interval, including the day of the earthquake of October 31, 2003, М = 7.0, at KOKUBUNJI GSIVS (Re ≈ 360 km, upper panel) and at YAMAGAWA GSIVS (Re ≈ 1300 km, lower panel). The day of the earthquake is marked by the vertical line with an arrow. The probable STIEPs are shown by shadowed ellipses.

Full size image

It follows from Fig. 1 that the maximum deviations in the parameters of δPEs and ΔfEsΣ are observed before the earthquake and in the middle of the studied preparation period but differ in length. The analysis of the hourly changes in the ionospheric parameters carried out by Korsunova and Khegai (2018) showed that the effects related to earthquake preparation last for 2–3 h and appear within 1 day. Therefore, only the one 1-day long maximum in Fig. 1 can be associated with the earthquake preparation. It is the day of its appearance that determines the earthquake moment lead time, which we designate here and further as ΔTδPEs. The maxima in the changes in diurnal Es characteristics lasting for longer than 1 day are determined by other geophysical factors related to the nature of the formation of the midlatitude sporadic Е layer and may exceed the precursor effects. Therefore, the absolute value of deviations in the Еs characteristics at the maxima immediately prior to an earthquake cannot be a criterion for the identification of a short-term ionospheric precursor. Such a criterion is the coincidence of the times of the appearance of maxima in both δPEs and ΔfEsΣ parameters at two observation stations located several hundred kilometers apart in accordance with the criteria proposed by Korsunova and Khegai (2018).

Below, Table 1 provides the characteristics for all 19 studied earthquakes: the magnitudes М, the radii of the preparation zones (ρD according to Dobrovolsky (1979) and ρS according to Sidorin (1992)) in km, and the distances from the epicenters to the GSIVS Re in km. The subscript “+” for the numbers in the columns for Re marks the cases for which Re > ρD, as well as the lead times of the earthquake day as determined based on the detected IEPs (ΔTδPEs, day). For comparison, we also indicated the lead times (ΔTh'Es, day) obtained earlier for the same earthquakes based on the hourly deviations of the virtual height h'Еs from the work by Korsunova and Khegai (2018). We can see that the lead times determined with the two methods coincides with an accuracy of up to a day for most of the earthquakes with М = 6.5–7.0. The lead time of the short-term precursor for earthquakes with М < 7.2 primarily does not exceed 1 day but increases for stronger earthquakes. In addition, for earthquakes with М > 7.2, the considered diurnal characteristics of the sporadic Е layer reveal the earlier occurrences of IEPs as compared to the occurrences obtained based on the hourly changes in the four ionospheric parameters: h'Es, foEs, fbEs, and foF2. We also note that the effects of earthquake preparations (the increase in δPEs and ΔfEsΣ) are sometimes also revealed at GSIVS located at the distances from the epicenters that exceed the radius of the earthquake preparation zone according to Dobrovolsky.

Table 1.   Parameters of the considered earthquakes and respective lead times ΔTδPEs and ΔTh'Es of possible ionospheric earthquake precursors that occur at the selected GSIVS pairs
Full size table

The above analysis is based on long-term data from manual ionogram processing in accordance with the International Instruction (Guidance …, 1977). However, most GSIVS are currently equipped with digital ionosondes with automatic ionogram processing, which records only one parameter of the sporadic E layer: foEs.

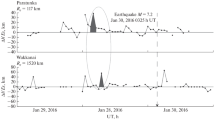
We compare two methods of ionogram processing (manual and automatic) in order ensure that the results of the detection of IEPs based on their data are adequate. For this purpose, we consider the data from Es measurements processed in two ways at KOKUBUNJI (Re = 250 km) and at WAKKANAI (Re = 770 km) during the preparation of the earthquake with М = 6.9 on November 22, 2016, that occurred under quiet geomagnetic conditions. Here, Re is the distance from the earthquake epicenter to the respective GSIV.

In accordance with the above procedure, we calculate the δРЕs and ΔfEsΣ parameters for the period of 10 days preceding the shock and the day of the earthquake. Figure 2 shows the results; it shows that the changes in each parameter are similar, although their values are different according to the data of manual and automatic ionogram processing over the time period in question. We note the coincidence of the time of appearance of maxima in the diurnal changes in both parameters immediately before the earthquake, which is typical of earthquakes with М = 6.8–7.0 (Table 1). These maxima are observed on the same day at stations spaced ~500 km apart, and this is a characteristic of STIEP occurrence according to Korsunova and Khegai (2018).

Fig. 2.
figure 2

Changes in diurnal parameters for δРЕs and ΔfEsΣ at the 11-day interval, including the day of the earthquake, November 22, 2016, М = 6.9, at KOKUBUNJI GSIVS (Re ≈ 250 km, upper panels) and at WAKKANAI GSIVS (Re ≈ 770 km, lower panel). Solid lines correspond to the values obtained with manual processing of the respective ionograms, and dash-and-dot lines show automatic processing. The day of the earthquake is marked by the vertical line with an arrow. The probable STIEPs are shown by shadowed ellipses.

Full size image

3 RESULTS AND DISCUSSION

Comparative analysis of the data from manual and automatic processing of the GSIVS ionograms showed some differences in the behavior of integral diurnal Еs parameters that are especially noticeable immediately before the earthquake. These differences are determined by the fact that all (even weak) reflections from Еs are recorded during manual processing of the ionograms and the most intense sporadic formations are fixed during automatic processing. Since there is an increasing total number of Еs occurrences before an earthquake, as mentioned in (Blaunstein and Hayakawa, 2009), then δРЕsman ≥ δРЕsautom. We note that the δРЕs maximum observed immediately before the earthquake at WAKKANAI GSIVS (Fig. 2) during automatic data processing is very weakly expressed, although it coincides in time with the δРЕs maximum observed during manual data processing. This is likely related to the fact that WAKKANAI GSIVS is located near the boundary of this earthquake preparation zone. Consequently, the most complete information on the changes in Еs during the period of earthquake preparation can be obtained only with manual processing of GSIVS ionograms. Nevertheless, at the final phase of a strong earthquake preparation with М ≥ 7.0 (Fig. 1) characterized by the appearance of intense sporadic formations, automatic processing of ionospheric measurements data allows the detection of possible short-term precursors of an impending seismic event. In addition, for a more accurate detection of STIEPs based on data from distant GSIVS, the latitudinal distance between the stations should not exceed 5°, i.e., the stations should be located in the same latitudinal zone, where the geophysical conditions of Еs formation are similar (e.g., Fig. 1, sec. 2). In this case, the diurnal characteristics δРЕs and ΔfEsΣ obtained from the measurements with digital ionosondes most fully reflect the changes in Еs that are typical of STIEPs. The results suggest that the measurement of ionospheric characteristics with digital ionosondes is an important supplement to the complex multiparametric observations of the lower ionosphere, especially in seismically active regions.

Analysis of the changes in the Еs parameters before all considered earthquakes (Table 1) shows that the diurnal characteristics δРЕs and ΔfEsΣ increase immediately before earthquakes with magnitudes of 6.5 ≤ М ≤ 7.2 (e.g., Fig. 1). This growth is characterized by the occurrence of a positive extremum in the behavior of δРЕs a day before the shock, which coincided with the local maximum of ΔfEsΣ. We note that the increase in δРЕs immediately before the earthquake at 35°–45° N is ~10–20% for М = 6.8–7.4 and that the deviations in ΔfEsΣ reach 0.6–0.8 MHz, which is ≈15–20% of the diurnal mean median values of foEs during the study period. We emphasize that the maxima of δРЕs and ΔfEsΣ before the earthquakes are recorded on the same day at two GSIVS located hundreds of kilometers apart. This fact corresponds to the criterion for the identification of the STIEP of an impending strong earthquake that is based on the appearance of anomalous changes in ionospheric parameters on the same day at GSIVS located hundreds of kilometers apart, according to the conclusions by Korsunova and Khegai (2018). Consequently, the diurnal characteristics δРЕs and ΔfEsΣ can be included in the group of previously studied parameters, such as h'Es, foEs, and fbEs, which are used to identify short-term ionospheric precursors in the Е region of the ionosphere.

Moreover, analysis of the ionosonde data from the Far East GSIVS in Magadan (Re ≈ 800 km) and Khabarovsk (Re ≈ 1500 km) before the Kamchatka earthquake of with М = 7.2 on January 30, 2016, made it possible to detect the probability of the occurrence PEs maxima on the same day immediately before the earthquake at both stations located more than 700 km from the earthquake epicenter. The increase in PEs was ~20%, which corresponds to the data obtained from the Japan GSIVS in the Pacific region (see above).

We note that the closeness of the lead times of the earthquake moments ΔTδPEs and ΔTh'Es immediately before the main shock (Table 1) indicates that the δРЕs and h'Es maxima are observed on the same day. We may suggest that a large number of sporadic layers also appears during the day before the earthquake at heights exceeding the ordinary levels of Еs formation at middle latitudes. For example, the formation of high-lying Еs layers before the earthquake agrees with the conclusions of the theoretical calculations by Kim et al. (1993) and Xu et al. (2020) as compared to ordinary conditions. It follows from these works that the high-lying sporadic layers can form at middle latitudes due to the penetration of the ionosphere by the seismogenic electric field.

4 CONCLUSIONS

The conducted analysis leads us to the following conclusions.

(1) The diurnal characteristics δРЕs and ΔfEsΣ obtained based on data from simultaneous measurements at two GSIVS located hundreds of kilometers apart allowed the detection of the possible STIEPs of an impending earthquake. The lead times of earthquake moments obtained in this work are similar to the lead times determined earlier for the same earthquakes in the hourly measured parameters of h'Es, foEs, and fbEs and amount to about a day for earthquakes with М = 6.5–7.2. In this respect, the possible STIEPs are sometimes observed beyond the earthquake preparation zone if its sizes are determined according to Dobrovolsky.

(2) The data from automatic ionogram processing with modern digital ionosondes less completely reflect the state of sporadic formations in the Е region of the ionosphere during the period of earthquake preparation; only intense layers are recorded. Nevertheless, they make it possible to identify STIEPs by the maxima in the changes in the characteristics for δРЕs and ΔfEsΣ.