Abstract
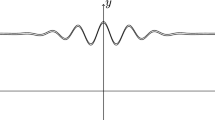
A family of plane solitary wave packets of a small (but finite) amplitude on the surface of an ideal incompressible fluid of finite depth beneath an ice cover is described. The solitary wave trains correspond to solutions of the two-dimensional system of Euler’s equations of an ideal incompressible fluid of the type of a traveling wave which decreases at infinity and has identical phase and group velocities. The ice cover is simulated by an elastic Kirchhoff-Love plate freely floating on the fluid surface in the compressed state.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A. T. Il’ichev, Solitary Waves in Fluid Dynamic Models (Fizmatlit, Moscow, 2003) [in Russian].
G. Iooss and K. Kirchgässner, “Bifurcation d’Ondes Solitaires en Présence d’une Faible Superficiele,” C. R. Acad. Sci. Paris, Ser. 1 311, 265–268 (1990).
F. Dias and G. Iooss, “Capillary-Gravity Solitary Waves with Damped Oscillations,” Physica D 65, 399–323 (1993).
P. Guyenne and E. I. Parau, “Finite-Depth Effects on Solitary Waves in a Floating Ice-Sheet,” J. Fluids and Structures 49, 242–262 (2014).
K. Kirchgässner, “Wave Solutions of Reversible Systems and Applications,” J. Diff. Eqns. 45, 113–127 (1982).
A. Mielke, “Reduction of Quasilinear Elliptic Equations in Cylindrical Domains with Applications,” Math. Meth. Appl. Sci. 10, 501–566 (1988).
G. Iooss and M. C. Perouéme, “Perturbed Homoclinic Solutions in Reversible 1:1 Resonance Vector Fields,” J. Diff. Eqns. 102, 62–88 (1993).
G. Iooss and M. Adelmeyer, Topics in Bifurcation Theory and Applications (2nd edition, World Scientific, Singapore, 1998).
M. Haragus and G. Iooss, Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems (Springer, Berlin, Heidelberg, 2012).
V. F. Pliss, “Reduction Principle in the Theory of Stability of Motion,” Dokl. Akad. Nauk SSSR 15, 1044–1046 (1964).
A. Vanderbauwhede and G. Iooss, “Center Manifold Theory in Infinite Dimensions,” Dynamics Reported 1, 125–163 (1992).
C. Elphick, M. E. Tirapegui, P. Brachet, P. Coullet, and G. Iooss, “A Simple Global Characterization of Normal Forms of Singular Vector Fields,” Physica D 29, 95–127 (1987).
A. Müller and R. Ettema, “Dynamic Response of an Icebreaker Hull to Ice Breaking,” in Proc. IAHR Ice Symp., Hamburg, 1984, Vol. 2, 287–296 (1984).
A. E. H. Love, A Treatise on the Mathematical Theory of Elasticity (Cambridge University Press, Cambridge, 1927).
L. K. Forbes, “Surface Waves of Large Amplitude beneath an Elastic Sheet. High Order Series Solution,” J. Fluid Mech. 169, 409–428 (1986).
D. E. Kheisin, Ice Cover Dynamics (Gidrometeoizdat, Leningrad, 1967) [in Russian].
V. A. Squire, R. J. Hosking, A. D. Kerr, and P. G. Langhorne, Moving Loads on Ice Plates (Kluver, Acad. Publ., Dordrecht, 1996).
G. Iooss and K. Kirchgässner, “Water Waves for Small Surface Tension: an Approach via Normal Form,” Proc. Roy. Soc. Edinburgh Ser. A. 122, 267–299 (1992).
T. Kato, Perturbation Theory of Linear Operators (Mir, Moscow, 1972).
A. T. Il’ichev and V. Ya. Tomashpol’skii, “Soliton-Like Structures on the Fluid Surface beneath an Ice Cover,” Teor. Mat. Fiz. 182, 267–283 (2015).
A. T. Il’ichev, “Solitary Wave Packets and Dark Solitons on the Water-Ice Interface,” Tr. Matem. Inst. RAN im. V. A. Steklova 289, 163–177 (2015).
A. T. Il’ichev, “Soliton-Like Structures on the Water-Ice Interface,” Usp. Mat. Nauk 70:6 426, 85–138 (2015).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © A.T. Il’ichev, 2016, published in Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, 2016, Vol. 51, No. 3, pp. 32–42.
Rights and permissions
About this article
Cite this article
Il’ichev, A.T. Solitary wave packets beneath a compressed ice cover. Fluid Dyn 51, 327–337 (2016). https://doi.org/10.1134/S0015462816030042
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0015462816030042