Abstract
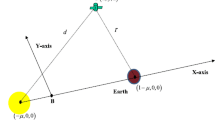
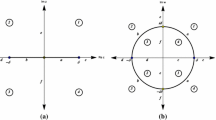
Equations of motion for the perturbed circular restricted three-body problem have been regularized in canonical variables in a moving coordinate system. Two different L-matrices of the fourth order are used in the regularization. Conditions for generalized symplecticity of the constructed transform have been checked. In the unperturbed case, the regular equations have a polynomial structure. The regular equations have been numerically integrated using the Runge–Kutta–Fehlberg method. The results of numerical experiments are given for the Earth–Moon system parameters taking into account the perturbation of the Sun for different L-matrices.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Egorov, V.A., Prostranstvennaya zadacha dostizheniya Luny (Spatial Problem of Reaching the Moon), Moscow: Nauka, 1965.
Szebehely, V., Theory of Orbits. The Restricted Problem of Three Bodies, New York: Academic, 1967.
Poleshchikov, S.M. and Kholopov, A.A., Teoriya L-matrits i regulyarizatsiya uravnenii dvizheniya v nebesnoi mekhanike (Theory of L-Matrices and Regularization of Motion Equations in Celestial Mechanics), Syktyvkar: SLI, 1999.
Poleshchikov, S.M., Regularization of motion equations with L-transformation and numerical integration of the regular equations, Celestial Mech. Dyn. Astron., 2003, vol. 85, no. 4, pp. 341–393.
Poleshchikov, S.M., Regularization of equations of the planar restricted problem of three bodies with L-transformations, Cosmic Res., 2015, vol. 53, no. 5, pp. 385–393.
Brouwer, D. and Clemens, G., Methods of Celestial Mechanics, New York: Academic, 1961; Moscow: Mir, 1964.
Broucke, R. and Lass, H., A note on relative motion in the general three-body problem, Celestial Mech., 1973, vol. 8, pp. 5–10.
Stifel, E. and Scheifele, G., Linear and Regular Celestial Mechanics, Berlin: Springer, 1971; Moscow: Mir, 1975.
Poleshchikov, S.M., Regularization of canonical equations of the two-body problem using a generalized KSmatrix, Cosmic Res., 1999, vol. 37, no. 3, pp. 302–308.
Poleshchikov, S.M., One integrable case of the perturbed two-body problem, Cosmic Res., 2004, vol. 42, no. 4, pp. 398–407.
Poleshchikov, S.M., The motion of a particle in perturbed field of an attracting center, Cosmic Res., 2007, vol. 45, no. 6, pp. 493–505.
Poleshchikov, S.M. and Zhubr, A.V., The family of potentials admitting integration of the perturbed twobody problem in regular coordinates, Cosmic Res., 2008, vol. 46, no. 3, pp. 202–214.
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © S.M. Poleshchikov, 2018, published in Kosmicheskie Issledovaniya, 2018, Vol. 56, No. 2, pp. 168–181.
Rights and permissions
About this article
Cite this article
Poleshchikov, S.M. Regularization of the Perturbed Spatial Restricted Three-Body Problem by L-Transformations. Cosmic Res 56, 151–163 (2018). https://doi.org/10.1134/S0010952518020077
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0010952518020077