Abstract
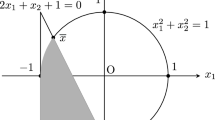
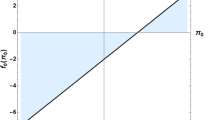
Use of the semidefinite relaxation in the problem of sign-definiteness of the quadratic form under quadratic constraints enables one to establish from the duality conditions an S-procedure. However, the S-procedure giving the necessary and sufficient conditions for signdefiniteness of the relaxed problem provides only the sufficient conditions for sign-definiteness for the original problem for the case of two and more quadratic constraints. This property is called the deficiency of S-procedure. A method was proposed enabling one in some cases to establish the conditional sign-definiteness in the case where the S-procedure provides a negative result. This method give the necessary and sufficient conditions for sign-definiteness in the two-dimensional case. An example was given.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Gelig, A.Kh., Leonov, G.A., and Yakubovich, V.A., Ustoichivost’ nelineinykh sistem s needinstvennym sostoyaniem ravnovesiya (Stability of Nonlinear Systems with Nonunique Equilibrium), Moscow: Nauka, 1978.
Polyak, B.T. and Shcherbakov, P.S., Robastnaya ustoichivost’ i upravlenie (Robust Stability and Control), Moscow: Nauka, 2002.
Yakubovich, V.A., S-procedure in the Nonlinear Theory of Control, Vestn. Leningr. Gos. Univ., 1971, no. 1, pp. 62–77.
Polyak, B.T., Convexity of Quadratic Transformations and Its Use in Control and Optimization, J. Optim. Theory App., 1998, vol. 99, no. 3, pp. 553–583.
Polik, I. and Terlaky, T., A Survey of the S-Lemma, SIAM Rev., 2007, vol. 49, no. 3, pp. 371–418.
Balakrishnan, V. and Vanderberghe, L., Semidefinite Programming Duality and Linear Time-invariant Systems, IEEE Trans. Automat. Control, 2003, vol. 48, no. 1, pp. 30–41.
Ibaraki, S. and Tomizuka, M., Rank Minimization Approach for Solving BMI Problems with Random Search, Proc. Am. Control Conf., Arlington, 2001, pp. 25–27.
Henrion, D. and Meinsma, G., Rank-one LMIs and Lyapunov’s Inequality, Proc. 39th IEEE Conf. on Decision and Control, Sydney, Australia, 2000, pp. 1483–1488.
Polyak, B. and Gryazina, E., Convexity/Nonconvexity Certificates for Power Flow Analysis, Advances in Energy System Optimization, in Proc. 1st Int. Symp. Energy Syst. Optim., New York: Springer, 2017, pp. 221–230.
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © L.B. Rapoport, 2018, published in Avtomatika i Telemekhanika, 2018, No. 11, pp. 150–158.
Rights and permissions
About this article
Cite this article
Rapoport, L.B. Semidefinite Relaxation and New Conditions for Sign-Definiteness of the Quadratic Form under Quadratic Constraints. Autom Remote Control 79, 2073–2079 (2018). https://doi.org/10.1134/S0005117918110103
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0005117918110103