Introduction

Since it has been proposed, the electromagnetically-induced transparency (EIT) effect has shown great potential in various applications, including slow light control, quantum information processing and sensing technology1,2,3. But the realization of EIT in atomic systems is a difficult task since some restrictions must be strictly fulfilled. In recent years, many studies have demonstrated that the EIT effect can be mimicked in classical optical coupled resonators due to its flexible design and easy implementation4,5,6,7,8,9,10,11. The optical EIT-like effect has been experimentally realized in many optical structures including coupled fiber systems4, coupled fused-silica spheres5, optical parameter oscillator cavities6, and the on-chip systems such as coupled silicon microring resonators7,8,9, microdisk resonators10, and photonic crystal microcavities11. However, most of these structures are immobile or only can be tuned by mechanical alignment12. It is difficult to realize the dynamic control of the transparency window without changing their geometrical parameters, which limits the practical application of EIT-like effect.

Graphene, a new material that has been available for only a decade, has generated great interest due to its exceptional properties such as high carrier mobility13, broadband absorption14,15, zero-band gap and tunable Fermi level16,17,18. In particular, the remarkable optical properties19 have made graphene a promising material for fast and broadband electro-optic devices such as photodetectors20,21 and modulators22,23,24,25. In these graphene integrated modulators, interband transitions and optical constants can be tuned through electrical gating. While the EIT-like effect in cascaded resonators has a specific relation with the optical constants of the resonators, confirming that graphene also has an excellent ability in controlling the EIT-like effect. Furthermore, all this structures are COMS-compatible.

In this work, we propose and experimentally demonstrate the EIT-like effect on graphene-silicon cascaded micoring resonators in which the transparency peak can be dynamically tuned via electrically control. By applying increasing voltage to the graphene/graphene capacitor which has been covered on one of the ring waveguides, regular changes of the EIT-like spectrum have been observed.

Results

Device design and fabrication

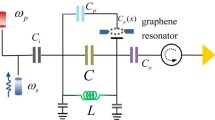
The structure of our device is depicted in Fig. 1a and b, showing the two cascaded ring resonators coupled with the bus waveguide. When light is coupled into the ring from the bus waveguide due to the evanescent field, the coherent interference between the properly designed coupled resonators will generate the EIT-like effect. In order to tune the transparency peak, two graphene layers which separated by an oxide are placed on the top ring. The sandwich structure formed by two graphene layers makes up a simple parallel capacitor model. The cross-sectional structure is shown in Fig. 1c. When a gate voltage is added, the two graphene layers are doped, one with holes and the other with electrons at the same doping level. causing a significant shift in Fermi energy (EF), which will in turn alter the rate of interband transitions and, subsequently, the optical transitions18.

Figure 1
figure 1

Device design.

(a) Over-all structure of the cascaded rings integrated with the graphene layers. (b) Functional region of the double graphene layers covering on the top ring. (c) Cross-section of the top ring covered with the bottom and top graphene layers separated by 20 nm Al2O3. (d) The corresponding TE mode-field profile of the 450 × 220 nm waveguide. (e) Electron microscopy of the functional region and the top graphene layer before the second Ti/Au contacts and the SiO2 upper cladding were deposited (f) Raman spectrum of the graphene sheet before transfer(black curve) and after transfer(red curve) to the device. After transfer, the G peak is at 1596 cm−1 and 2D peak is at 2692 cm−1.

Full size image

The device was fabricated on commercial SOI wafers, having a silicon thickness of 220 nm and a buried-oxide thickness of 3 μm. The bus waveguide and the two cascaded ring resonators were fully etched, with the depth of 220 nm and a width of 450 nm, to guide single-mode transverse electric (TE) light (Fig. 1d). The radii of the two ring resonators were designed to be 20 μm. Two gaps, between the two rings and between the ring and bus waveguide, were designed to have the same length, approximately equal to 90 nm approximately which was found to be the optimum coupling distance for our device. At both ends of the bus waveguide, a pair of grating couplers was fabricated with a 600 nm period, in order to couple light in and out of the devices. Before transferring graphene layer, a 5 nm atomic layer deposited (ALD) Al2O3 was employed to prevent potential carrier injections from the bottom graphene layer into the silicon23. A graphene/graphene capacitor was fabricated above the top ring resonator. The capacitor consists of two sheets of monolayer graphene grown by means of chemical vapour deposition (CVD) on copper foil and wet-transferred on our silicon device (see method). The electron microscopy of the functional region and the top graphene layer before the second Ti/Au contacts and the SiO2 upper cladding were deposited are shown in Fig. 1e and we can see a high quality coverage of graphene on the silicon substrate and the waveguide. Raman spectrum of the graphene sheet before and after transfer to the device is shown in Fig. 1f. The oxide between two graphene layers was 20 nm Al2O3, obtained using the same ALD method. To apply voltage to the capacitor Ti/Au (10/100 nm) contacts were used for both layers of graphene by electron-beam evaporation. We then provided 1 μm-thick SiO2 upper cladding deposited by plasma-enhanced chemical vapor deposition to avoid the loss caused by metal contact.

Theoretical description of the tunable optical transparency mechanism

When a bias voltage Vb is added, the change of the carrier concentrations in graphene can be expressed as where V0 is the offset voltage caused by natural doping, ε0 and ε are the permittivities of free space and of Al2O3, respectively, and t is the thickness of the Al2O3 between the two graphene layers, e is charge of the electron. Thus, the Fermi level of graphene will be shift as , where ħ is the Plank constant divided by 2π and vF is the Fermi velocity. When the bias voltage dependent Fermi level EF(Vb) is close to the Dirac point, interband absorption will occur as electrons are excited by the incoming photons (). When this occurs, the graphene layers will not be transparent22. On the other hand, when EF(Vb) is greater than half of the photon energy of incident light (), all electron states are filled up in graphene and no interband transition is allowed due to the Pauli blocking. In this condition, graphene layers become transparent. As a consequence of the absorption change in the graphene layers, the ring waveguide under them will experience a significant change in round-trip loss. According to the mechanism of the EIT-like effect in optic resonators, the loss of the top ring waveguide has a specific influence on the transparency window (Supplementary Note 1). The cascaded optical transparency window varies with the attenuation factor coefficient of the top ring. The increase of the attenuation entails a decrease of the round trip loss, which has a direct correlation with the absorption of graphene (Supplementary Fig. 1b). The relationship between the Fermi level and the EIT-like effect can be illustrated as in Fig. 2. When bias voltage is low, both graphene layers are lightly doped () and thus opaque, inducing a high loss in the ring waveguide and the EIT-like effect will not occur if the graphene lays has enough coverage (Fig. 2a). When bias voltage is large, both graphene layers are heavily doped, by electrons and holes respectively (), and thus transparent. As a consequence the ring waveguide has low loss and the EIT-like effect will occur (Fig. 2b). Therefore, according to this theory, the EIT effect can be dynamic tuned by changing the bias voltage without changing the geometrical parameters of the device.

Figure 2
figure 2

Relationship between the Fermi level and the EIT-like effect.

(a) At low bias voltage, the Fermi level is close to the Dirac point, light transmission in the top ring is absorbed by the graphene layers and EIT-like effect does not occur. (b) At large bias voltage, no interband transition occurs, the graphene layers are transparent and the EIT-like effect is significant.

Full size image

Device measurement

The tunability of the graphene-ring resonator based EIT-like device is investigated by applying different bias voltages. For zero bias voltage, Fermi level is closed to the Dirac point and the top ring has relative high loss and the EIT-like effect is consequently weak (Fig. 3a), corresponding to the condition shown in Fig. 2a. We can notice that there is still a small transparency peak at 0 V bias, indicating that the EIT-like optical interference still exist between the cascaded rings at this loss condition. Figure 3a also shows the transparency windows in 2 V and −2 V bias voltages in which we can see that the 2 V and −2 V curves are not coincident. Having designed the device, it is known the two graphene layers covered on the top ring are equivalent and therefore should have the same response to bias voltages having the same absolute value. We can ascribe this difference to the different processing technologies adopted for Al2O3 and SiO2, which modify the surrounding environments of the two graphene layers. The top layer is in contact with Al2O3 on one side and with SiO2 on the other; the bottom layer is instead sandwiched between two Al2O3 layers23. With the bias voltage increasing from 2 to 6 V, the transparency peak become significant, as shown in Fig. 3b. This is a direct consequence of blocked graphene optical absorption with the increasing doping level, which leads to a lower loss. Ideally, the EIT-like transparency peak should emerge instantaneously when the Fermi level is increased above the threshold (or lowered below ) as shown in Fig. 2. However, the loss in the top ring is essentially determined by the imaginary part of the effective index (neff) of the graphene-silicon waveguide, which is mainly decided by the Fermi level-dependent dielectric constant (εg) of graphene. The dielectric constant εg can be obtained through 26, where ω is the frequency, tg is the thickness of the graphene layer, and σ is the optical conductivity of graphene. The overall mode in the graphene-silicon waveguide displays a Gaussian distribution. The graphene layers only capture very few portions of the fields and the fields outside the graphene layer cannot feel εg variations27. As a consequence, the transmission in the graphene-silicon waveguide varies gently around the threshold . In other words, the interband transition induced absorption is broadened and the transparency window will have a gradual change with the shift of the Fermi level. This is one reason why the EIT-like transparency peak varies gently with the increase of the bias voltage. While the other one which associate with the interband relaxation time will be described in the following paragraphs. With the voltage increasing from 6 to 10 V, the increase of amplitude of the transparency peak is no longer significant, as shown in Fig. 3c. This indicates that the loss induced by graphene has been lowered to a minimum due to the Pauli blocking and the loss is now mainly attributable to the silicon waveguide. Meanwhile, the wavelength spectrum has a red shift with the voltage increasing from 2 to 6 V (Fig. 3b), and a blue shift from 6 to 10 V (Fig. 3c). This can be attributed to the real part of the dielectric constant (εg′) of graphene which changes with the voltage-dependent Fermi level and is similar to the resonance frequency shifts observed in optical plasmon resonance with graphene28, as we describe below.

Figure 3
figure 3

EIT-like effect controlled by bias voltage.

(a) Transparency window at the d.c. voltage of 0 V (orange curve), 2 V (magenta curve) and −2 V (green curve). The curves at 2 V and −2 V are not coincident due to the different environments for the two graphene layers. (b) Increasingly apparent transparency peak and the red shift with the increase of the voltage from 2 V (green curve) to 4 V (red curve), then 6 V (magenta curve). The broadened absorption of graphene leads to a gradual change of transparency peak. (c) Interband transitions are blocked when voltage is larger than 6 V so the peak value no longer increases and only the blue shift changes is observed with the increasing voltage. (d) Experimental and theoretical shift of the transparency peak with the variation of the voltage. The red and blue shifts of the transparency peak are due to an increase and subsequent decrease of in graphene.

Full size image

The real and imaginary parts of the complex dielectric constant, εg′ and εg″, of graphene can be obtained from its optical conductivity (σ), which can be derived from the Kubo formula in a complex form consisting of interband and intraband contributions29,30

where is the photon energy of the incident light, set to 0.805 eV at the region of incident light we choosed (i.e., at the wavelength of 1544 nm). is the relaxation time associated with carrier-carrier intraband collisions and phonon emission and τ2 is the relaxation time associated with electron interband relaxation and cooling of hot phonons31,32,33,34. The term can be set to zero because the the relaxation time associated with intraband transition usually in the order of the hundreds femtosecond31 and thus it has little effect on the dielectric constant. Here we set , which can be treated as the interband transition broadening28,35. The value of τ2 has been measured on a picosecond scale33,34, but the value of Γ is usually enlarged owing to the defects in graphene. This is another reason why the EIT-like transparency peak varies gently with the increase of the bias voltage (Supplementary Fig. 2b). Equation 2 shows that experiences a step-like decrease when the Fermi level is above the threshold indicating that the interband transitions are blocked. This is because the overall mode index in the graphene-silicon waveguide neff is proportional to graphene’s dielectric constant εg in both real and imaginary parts27. The imaginary part of the index Im(neff) represents the loss in the waveguide and it is the same for . shows the same trend with the real part of the index Re(neff) which has a proportional relationship with the wavelength shift of the transmission curve (Supplementary Note 1). Therefore, the red and blue shift of the transparency peak can be well explained by the character of . When , increases with the increasing of EF(Vb) and so does Re(neff), so the transparency curve has a red shift (Fig. 3b). When , decreases with the increasing of EF(Vb) and so does Re(neff), so the transparency curve has a blue shift (Fig. 3c). Figure 3d shows the experimental shift of the transparency peak with the variation of the bias voltage. The theoretical curve simulated by agrees well with the experimental result. In the course of the theoretical simulation, EF + 0.24 eV was used instead of EF in equation 2 because the natural doping in graphene has a shift in the Fermi level, as will be described below.

From equation 1, it is possible to notice that peaks around EF = 0.4 eV (i.e. the threshold ) and the corresponding bias voltage of 3.9 V can be calculated using the relationship, where as estimated from a parallel-plate capacitor model of our device. From the Raman spectroscopy (Fig. 1f) we can estimate a p-type doping approximately equal to 4.4 × 1012cm−2 (Supplementary Note 2) and thus the corresponding zero bias voltage Fermi level EF = 0.24 eV and the offset voltage V0 = 1.46 V can be obtained. As a result, the bias voltage relevant to the transmission threshold can be calculated to be equal to 5.36 V. However, either the saturate of the peak value (Fig. 3c) or the bending of the transparency peak shift (Fig. 3d) indicate that the threshold voltage is around 6 V. The small difference of the threshold voltage can be attributed to the quantum capacitance of graphene which has been measured on a microfarad per square centimeter scale36.

Discussion

We have experimentally demonstrated, for the first time to our knowledge, the tunable optical analog to electromagnetically induced transparency on chip by integrating monolayer graphene with the cascaded microring resonators. The relationship between the EIT-like effect and the voltage dependent Fermi level of graphene has been investigated through both theoretical studies and experimental measurements. The transmission spectra reveal that the structure possesses a prominent transparency peak at the threshold voltage of 6 V, indicating that the Fermi level of graphene has reached half of the photon energy (i.e. 0.4 eV) at this voltage. Furthermore, the red and blue shifts of the transparency window have been well explained in terms of the real part of the dielectric constant of graphene. Our results will provide important guidelines for the design and use of tunable optical EIT devices which have promising applications in slow light, quantum information processing and sensing technology, and provide a new method for the manipulation and transmission of light in highly integrated optical circuits. Furthermore, compare with the mechanical tuning of the EIT-like effect, the tuning speed of the device could be as high as the one obtained with modulators22,23,24,25 which utilize the graphene in a similar way. This feature may be useful in some special cases of fast on-chip optical communications.

Methods

Device fabrication

The cascaded ring waveguides were fabricated in the SOI wafer with a silicon thickness of 220 nm and a buried-oxide thickness of 3 μm. E-beam lithography (EBL) and inductively coupled plasma (ICP) etching were used to fabricate the 220 × 450 nm waveguides and the 300 × 300 nm gratings. The region for graphene transfer (the etching era for the top ring) was broadened to obtain a good coverage of graphene. Before the transfer of the bottom graphene, 5 nm isolation layer deposited (ALD) Al2O3 was used to prevent potential carrier injections from the bottom graphene layer into the silicon. 200 nm thick polymethyl methacrylate (PMMA) was spin-coated onto the graphene sheet which was grown by chemical vapour deposition (CVD) on Cu film and baked at 200 °C for 1 min. The copper foil was then removed using FeCl3 solution and the graphene sheet, coated with PMMA, was transferred onto the device. Finally, the PMMA was removed using acetone and the residue was rinsed with isopropanol to obtain a clean graphene surface. To remove the unwanted part of graphene, the deep-ultraviolet lithography and oxygen plasma were used. Before deposing the sandwich 20 nm Al2O3, 10 nm Ti and 50 nm Au were deposited by electron-beam evaporation and patterned by a lift-off process. This was done to protect the bottom graphene from the sandwich Al2O3 etching process for electric contacting. Owing to the hydrophobic nature of the graphene basal plane, it is difficult to depose Al2O3 directly on it. For this reason, before deposing Al2O3, a 1 nm aluminum layer was evaporated using electron-beam evaporation and immediately oxidized into Al2O3 in ambient air23. Using the 1 nm Al2O3 as the seed layer, the sandwich Al2O3 was then deposited on the device. In order to contact the electrode with the bottom graphene layer, which was fully covered by Al2O3, reactive ion etching (RIE) was used to remove a patch of Al2O3 from the Ti/Au (10/50 nm) which had been previously deposed. The transfer procedures used for top graphene layer was the same with the bottom one. The final device was then covered with 1 μm-thick SiO2 deposited by plasma-enhanced chemical vapor deposition (PECVD) and drilled by RIE to contact the two graphene layers with the electrode.

Additional Information

How to cite this article: Wang, Y. et al. Tunable optical analog to electromagnetically induced transparency in graphene-ring resonators system. Sci. Rep. 6, 38891; doi: 10.1038/srep38891 (2016).

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.