Introduction

Synchronization plays a crucial role in a wide spectrum of technological, biological, and social networks1,2,3,4. Even though studied intensively under various aspects5,6,7,8,9,10,11, yet a full clarification is needed on the effects of time-dependent coupling structures12,13,14,15,16, particularly for those circumstances for which the coupling strengths (or connection topologies) may switch in time. For the specific condition (termed as the blinking network case) for which the graph structure changes much more rapidly than the units’ dynamics, a comprehensive theoretical framework was established, and applications were developed accordingly17,18,19. However, such an extreme situation does not properly match the generic case, as in the majority of real-world systems the time scale for the coupling evolution turns out to be in fact secular with respect to that of the individual dynamics. For instance, the time scales of synaptic plasticity (the basis of most models in neural circuits) is known to expand from milliseconds to days20,21,22,23, and long term plasticity between neurons is actually thought to be the real clue for the higher level functioning of the brain, such as long term memory24. A further example is evolutionary processes leading to mutations in genetic networks, which evidently take place over timescales much longer than those related to genetic expressions. Moreover, based on minimal models of interacting binary state nodes, different time scales of coupling switching may even lead the network into distinct phases of collective behavior25.

Synchronization in slow-switching networks calls still for a general theory, and for elucidation. Despite the importance of the issue, current studies are so far limited to either simple unit dynamics (e.g. linear system26), or simple coupling dynamics (e.g. on-off coupling27,28), or continuous switching processes29. In this paper, we provide instead the general criteria for stable synchronization in slowly varying networked systems, and demonstrate that the stability of synchronization is fully characterized by the largest Lyapunov exponents of the transverse modes associated to the varying structures. Comparison to the fast-switching case allows to show that enhancement of synchronization can be predicted from the profile of the master stability function (MSF). Moreover, a network controlling strategy can be sorted out from our results, which embeds a controlling structure into the system, predesigned as a standard one (i.e. regardless of the specific topology to be controlled), in a way that it may find applications even to systems whose structures are unknown.

Model and Theory

We start by considering a networked system with N identical systems, described as , with i = 1, 2, , N, , and . The units interact with their neighbors, so that the dynamics of the i-th node is ruled by , where σ is the coupling strength, gij is the element of Laplacian G, and specifies the output function through which coupling is realized among the networks’ units. Let furthermore x1 = x2 = … = xN ≡ xS be the synchronized solution and δxi ≡ xi − xS the m dimensional vector accounting for the deviation in time between the evolution of the network’s node i and the synchronized state.

For static networks (i.e. when G does not change in time), the linearized equation of the system (around xS) is expressed as

where δx = (δx1, , δxN)T, and DF and DH are the Jacobian functions of F and H, respectively, evaluated on the synchronized solution xS. By plugging into Eq. (1) (where λ1 = 0 < λ2 <  < λN are the eigenvalues and {uj} the corresponding eigenvectors providing an orthonormal basis of ), and setting δx(t) = Qδy(t) [with Q = (u1, , uN)⊗Im) and δy = (δy1, , δyN)T], one obtains

The largest Lyapunov exponent of the transverse mode δyj is defined as

which is a function of the eigenvalue λj and coupling strength σ, also known as the Master Stability Function (MSF). The necessary condition for having a stable synchronization is that MSF Φ(σλj) is negative for all the transverse modes j ≥ 2, as elaborated in ref. 11.

Now, let us consider the case of time-varying networks where the Laplacian G is composed of a sequence of coupling matrices (G1, G2, ) that occur in a chronological order. Suppose, further, that Gk lasts for a lapse τk under coupling strength σk (a condition that we will denote as {Gk, τk, σk}). Then G(t) is represented by G(t) = ({G1, τ1, σ1}, {G2, τ2, σ2}, ).

To elucidate the effect of a slow switching, we start from the simplest case that the network alternates between two structures (G1 and G2), so that the system periodically switches between configurations {G1, τ1, σ1} and {G2, τ2, σ2}, with a period T = τ1 + τ2. Again taking and , one obtains that the necessary condition of stable synchronization is the following: for each pair of transverse modes (j, l ≥ 2), if Slj ≠ 0 where Slj = vlTuj, one should have (see Methods, part I for details)

The condition is readily extended to the general case of a network that slowly switches among a sequence of L configurations, i.e. ({G1, τ1, σ1}, , {GL, τL, σL}) with : for each combination of the transverse modes of the L configurations (j1, j2, , jL), if all the L − 1 pairs of vectors () (2 ≤ k ≤ L) are non-orthogonal, one should have

With the conditions (4, 5), for any function the MSF Φ(σλj) is, indeed, obtained straightforwardly, and once one has the specific sets of eigenvalues and eigenvectors that diagonalize the L configurations, the specific values of can be simply read on the unique MSF for each 2 ≤ k ≤ L, so that predictions on the stability of synchronization can be elegantly made by checking whether conditions (4, 5) are fulfilled. In the following, we will therefore linger on some practical applications of our theory.

Results

In this paper, we consider the case of Rössler oscillators where the unit dynamics is described by , , with and parameters being a = b = 0.2, and c = 7. H is a 3 × 3 matrix, whose elements are 1 for h11 and 0 otherwise, i.e it realizes a linear coupling on the x1 variable of the graph’s units. Dynamics is integrated with a fixed time step Δt = 0.001, and the synchronization performance is evaluated by the error function defined as

where 〈⋅〉 denotes the time average over a sufficient long time after discarding transient processes.

Validation of Analytic Predictions

To validate the analytic prediction, we first consider a simple case of a network made of just three oscillators, which switches between two structures along the same time interval τ. The Laplacians of the two connection arrangements are and with u1 = v1 = (1, 1, 1)T and (which is along the synchronization manifold x1 = x2 = x3). For simplicity, we set σ1 = σ2 = 1, u2 = v2, and u3 = v3, and thus Sjl = δjl. According to Eq. (4), the system is stable on the synchronization manifold when for j = 2 and 3, respectively. Figure 1(a) reports the synchronization index 〈δ〉 in the (, ) plane, where the values of and are fixed as 3. Notice that the solid lines [obtained from the equations for j = 2 and 3, respectively] separate the plane into two regions: the white one (synchronized dynamics) and the dark one (asynchronous behavior), in good agreement with the numerical results. It is remarkable that this result is pertinent to a specific choice for the switching time (τ = 10). Since this result pertains to the slow-switching scenario, it is worth exploring the range of τ for which the overall scenario is actually maintained. Figure 1(b) reports 〈δ〉 vs. τ, for and [the solid spot in (a)]. 〈δ〉 vanishes for τ ≥ 2, whereas it diverges for τ < 2 (i.e. when the structures start to switch faster).

Figure 1
figure 1

(a) Gray plot of 〈δ〉 in the () plane, for and σ1 = σ2 = 1. Solid lines indicate the predicted boundaries of the synchronization region. Dashed lines indicate the boundaries for the case of fast switching. , and . (b) 〈δ〉 vs. τ for the case and [indicated by a solid dot in panel (a)]. Inset: Thick black curve shows a typical trajectory of the Rössler oscillator projected on xy-plane for the lapse of time τ = 2. Thin line reports the actual continuation of that trajectory, and serves as a guide for eye.

Full size image

In fact, as soon as the switching process occurs over fast enough time scales, a sufficient condition is that the time average of the coupling matrices supports synchronization17,18. In particular, when G1 and G2 share the same basis, i.e. uj = vj for all j, an equivalent condition for fast-switching networks can be obtained, that is: for 2 ≤ j ≤ N (see Methods, part II for details). For comparison, this latter condition is reported with dashed lines in Fig. 1(a). As the region delimited by the dashed lines is embraced in that contoured by solid lines, we may conclude that in this case a slow switching scheme is prompting synchronization more than a fast switching one.

The Shape of Master Stability Function

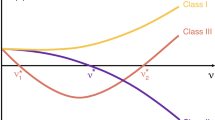
A second remarkable application is the prediction, under fixed topology and switching coupling strengths, of the most favorable switching scheme for synchronization. The conditions of slow (large τ) and fast (small τ) switching schemes lead, indeed, to a general criterion for a class of networks whose coupling strength may vary with time while the Laplacian G is fixed, for example networks with on-off coupling27. Specifically, for the case that the coupling strength switches between two values σ1 and σ2 alternatively, the criterion (which can be readily extended to general case of arbitrary number of different values) can be stated as follows: when the MSF is concave in the domain spanned by the Laplacian eigenvalues, i.e. αΦ(x1) + (1 − α)Φ(x2) ≤ Φ[αx1 + (1 − α)x2], if the network supports a synchronous dynamics under a fast switching [i.e. ( ∀ j ≥ 2)], the same network will also behave synchronously under slow switching of the same structures [i.e. ( ∀ j ≥ 2)]. When instead the MSF is convex, the situation is reversed, and slow switching conditions include the fast switching ones.

In order to better elucidate the above relationship between the two switching schemes, we take the case of a complete network, for which all non-vanishing eigenvalues of the Laplacian are the same, λ2 = λ3 =  = λN = N, so that the N − 1 transverse eigenmodes form an (N − 1)-dimensional linear subspace. Specifically, we preserve the network structure as a complete graph, and switch the coupling strength between σ1 and σ2 with the same time interval τ, so that the argument σλ of the MSF is (for all transverse modes) switched between σ1N and σ2N. Noting that the associated conditions for stable synchronization are (fast switching) and (slow switching).

Figure 2 reports the results for the cases of τ = Δt = 0.001 (fast switching, panel (a)) and τ = 104Δt = 10 (slow switching, panel (b)), where σ1 is fixed at 3/N so that σ1N = 3, and σ2N goes from 3 to 15 (being the MSF concave in the corresponding domain). The MSF for the considered Rössler chaotic dynamics is shown in panels (c) and (d). The long dashed lines crossing panels (a) (red lines) and (b) (green lines) show the boundaries of σ2N for synchronization, coming from the conditions and , respectively. Dashed lines in (c) and (d) indicate how one can predict the boundaries with just the help of the shape of the MSF (details in the caption). Theory and the numerical results match very well. It is clearly shown that the range spanned by the green dashed lines in panel (d) is larger than that spanned by the red dashed line in panel (c), which confirms the our conclusion that when the MSF is concave in the domain concerned, the case of slow switching allows synchronization for a range of σ2N larger than that of fast switching. While this example considers explicitly a concave MSF, the case of a convex MSF is described and reported in the Supplementary Information.

Figure 2
figure 2

Upper panels: 〈δ〉 vs. σ2N for τ = 10−3 [fast switching, panel (a)] and τ = 10 [slow switching, panel (b)]. N = 100 and σ1N = 3. Lower panels: the MSF corresponding to our choice of the Rössler chaotic oscillator. In panel (c), the red dashed lines pointed by the red arrows indicate the value of σ1N = 3 (the left one), and σ2N which satisfies (the right one), therefore giving the equal length of the two arrows. In panel (d), the red dashed lines pointed by the red arrows indicate the value of Φ(σ1N = 3) (the lower one), and Φ(σ2N) which satisfies (the upper one), and also the equal length of the two arrows. The green dashed lines indicate the corresponding values of σ1N = 3 and σ2N. The results are averaged over 50 realizations.

Full size image

A Control Strategy

As a last step of our study, we show how the discovered conditions suggest the realization of controlling strategies for inducing synchronization in generic networks. Specifically, we introduce a heuristic approach, whose main idea is to periodically add a controlling network into a pristine graph, in a way that the whole network switches alternatively between the original topology (i.e. the target network to be controlled) and the controlling structure. This latter structure is actually chosen in order that the resulting time-evolving graph satisfies the conditions for stable synchronization provided in the above. In fact, the spectrum of the Laplacian of the original network may be very different from one to another, with more heterogeneous graphs displaying larger ranges of eigenvalues’ spectrum30. Thus, finding a proper controlling structure for each specific original network is a key step in this strategy.

Having to cope with a generic case, we here propose a controlling structure (a graph) for which the non null eigenvalues of the Laplacian are all the same, say λ, and the coupling strength σ is chosen such that Φ(σλ) = Φmin (where Φmin is the minimum value of the MSF). Because the values of MSF for all the transverse modes reach Φmin, this kind of networks is optimal for synchronization, and we refer to them as Optimal synchronization networks (OSN). For binary interaction networks (those represented by adjacency matrices), the number of optional OSNs could be very large. A practical way of constructing an OSN is provided in ref. 31.

Now suppose that, during each period, the pristine network stays fixed for a time τU, and then the system switches to an OSN which remains fixed for a time τO. Noted that, regardless the specific spectrum of the original graph, the possible values of Φ will never exceed the maximum value of the MSF, Φmax. Therefore, according to our condition for slow switching, the graph will be controlled when τO/τU ≥ Φmax/|Φmin|, no matter what its structure is. For our specific choice of Rössler system, and , one may expect that any network can be controlled when .

To validate our predictions, we generate homogeneous and heterogenous networks of size N = 100 by means of the Erdös-Rényi (ER32) and Barabási-Albert (BA33) models, and adopt complete networks as controlling structures (other choices of OSNs were considered and similar results, not shown here, were obtained). According to the condition for slow switching, the threshold of the ratio τO/τU for the controlling procedure is fully determined by the transverse mode which has the largest MSF value among all the others. By denoting the largest MSF value reached by this mode as ΦL, the synchronization condition requires τO/τU ≥ ΦL/|Φmin|. The inset of Fig. 3 reports the values of ΦL. When σ = 1, ΦL is relatively small for both ER and BA networks, and therefore the graphs can be controlled with a small ratio τO/τU(≥ΦL/|Φmin|), as shown in the main panel of Fig. 3. When σ = 2, the value of ΦL increases, and a larger ratio of τO/τU is needed. However, a further increase in σ leads to the saturation of ΦL at Φmax, and to the convergence of the ratio τO/τU to the expected threshold value (about 0.4), as indicated by the arrow in the main panel of the figure.

Figure 3
figure 3

〈δ〉 as a function of the ratio τO/τU with τO fixed at τO = 10, for ER and BA networks with different coupling strength σ (see the legend for the color code).

The arrow indicates the value of . The inset shows the largest MSF value ΦL of these networks. The reported results refer to ensemble averages over 50 different realizations.

Full size image

Discussion

In conclusion, we succeeded in setting the necessary condition for stable synchronization of slowly switching networks. Together with the criterion of fast switching networks in previous works, the both ends of the related condition of switching networks now have been filled. As a contrast to fast switching networks, for slowly switching networks, the condition of stable synchronization is affected by the largest Lyapunov exponent of each transversal mode of switching structures rather than that of their aggregation. Interestingly, we find that such difference in the two switching schemes help us, with the shape of the Master stability function (MSF), in predicting which switching scheme is more favourable for synchronization. Specifically, when the MSF is concave (convex) in the domain the argument span, the network supports a synchronous dynamic under a fast (slow) switching, the same network also behaves synchronously under slow (fast) switching of the same structures. This result further exploits the information embedded in the MSF, from the number and positions of the null points to the shape of it.

The results about slow switching networks may provide potential applications. In this paper, we propose a heuristic controlling strategy according to the characteristic of slow switching networks, where a controlling structure is inserted to the target network periodically. To make this strategy to be general for different situations, we introduce the optimal synchronization networks (OSN) (graphs whose largest Lyapunov exponents of all the transverse modes are close to the minimum value of the Master Stability Function) and show that they serve as an excellent class of controlling networks. In particular, with the knowledge of MSF, the ratio between the action times of OSN and target networks could be preassigned as a standard, and the target networks could be controlled regardless of their specific structure or coupling strength. Therefore, this strategy has potential applications to a wide variety of systems, with unbounded coupling and unknown structure.

We highlight that the obtained condition of stable synchronization is necessary but not sufficient, which roots from the fundamental limitation of MSF which only assesses local stability of the synchronized state. Sufficient conditions may, in limited situations, be derived from global stability analysis, such as Lyapunov function methods.

Methods

Condition of stable synchronization of slowly switching networks

Let us start from the original case of a network which is fixed on a single structure. While the condition, for this case, has been obtained by Pecora et al. in ref. 11, we shall further elaborate on the details of the analytic procedure, which will be helpful to further understand the general case of slow-switching networks.

The linearized equation of the system deviating around the solution xS ≡ x1 = x2 = .... = xN is expressed as

where the meaning of the notations are the same as those in the main text. The Laplacian G could be decomposed as where {λj} is the spectrum with λ1 = 0 and {uj} the eigenvectors with u1 corresponding to the synchronization manifold. Taking now IN as , one gets

Setting δx(t) = Qδy(t) with Q = (u1, , uN)⊗Im, Eq. (8) becomes

where ej is a unit vector whose j-th element is 1 and 0 otherwise. The matrix in Eq. (9) is block diagonal with m × m blocks. Taking δy as δy = (δy1, , δyN) with , one has

Generally, DF + σλjDH varies with the evolution of the state yj, so we can denote DF + σλjDH as . Since , the solution of δyj can be expressed as

where δyj(0) is the initial condition, Δt = t/M, and . The M → ∞ limit procedure gives the formal integral

where stands for time-ordered integration, reflecting the continuum limit of the successive left multiplications in Eq. (11). Denoting , Eq. (12) becomes

Now, for ergodic systems, is asymptotically (i.e. at large enough t) independent of t, and

Therefore, if one defines as the largest Lyapunov exponent associated to the j-th eigen-mode

one has when t is large. Stable synchronization requires (as a necessary condition) the largest Lyapunov exponents Φ(σλj) to be negative for all the transverse eigen-modes (j ≥ 2).

Finally, according to Eq. (13), the solution of δy is

and therefore

Suppose now that a network periodically switches between two configurations {G1, τ1, σ1} and {G2, τ2, σ2}, with τ1 and τ2 being the lasting times of the two configurations and σ1 and σ2 the coupling strengths, respectively. Similarly to the above, one can decompose G1 and G2 as and . For each period T = τ1 + τ2 (supposing G1 acts first), the state δx attained by at time T can be written as

We define Slj = vlTuj, so that vlvlTujujT = ∑j′uj′ujTSj′lSlj. Then Eq. (18) can be rewritten as

Taking again δx = Qδy, one eventually gets

Remarkably, when ej′ejT acts on a vector, it actually picks its component on the direction ej and turns it into the direction ej′. Thus, one obtains

When τ1 and τ2 are large, we have

The stable synchronization demands the convergence of |δyj′(T)| which accounts for the condition that: for each pair of (j, l ≥ 2), if Slj ≠ 0, then one should have

as stated in Eq. (4). In analogy, the condition could be directly extended to the general case of arbitrary number of configurations, as formulated by Eq. (5).

Condition of stable synchronization of fast switching networks

For the case of fast-switching, we also start from the situation that a network periodically switches between two configurations {G1, τ1, σ1} and {G2, τ2, σ2}, while here τ1 and τ2 are sufficiently small. It has been found that the condition of stable synchronization for fast-switching networks is that the time average of the coupling matrices supports synchronization17.

Now, we look at a specific case that and share the same basis, i.e. uj = vj for all j and therefore Slj = δlj. In this case, stable synchronization could be attained when for all the transverse modes one has

This result is readily extended to a general situation of networks fast switching among arbitrarily number of configurations. The condition of stable synchronization now is

where notations are similar to those in the Eq. (5) of the main text. We note that this case that the Laplacians of all the configurations share the same basis covers a large class of network whose coupling strength varies with time but structure fixes.

Additional Information

How to cite this article: Zhou, J. et al. Synchronization in slowly switching networks of coupled oscillators. Sci. Rep. 6, 35979; doi: 10.1038/srep35979 (2016).