Abstract
We experimentally demonstrate and characterize a four-qubit linear-optical quantum logic circuit. Our robust and versatile scheme exploits encoding of two qubits into polarization and path degrees of single photons and involves two crossed inherently stable interferometers. This approach allows us to design a complex quantum logic circuit that combines a genuine four-qubit C3Z gate and several two-qubit and single-qubit gates. The C3Z gate introduces a sign flip if and only if all four qubits are in the computational state |1〉. We verify high-fidelity performance of this central four-qubit gate using Hofmann bounds on quantum gate fidelity and Monte Carlo fidelity sampling. We also experimentally demonstrate that the quantum logic circuit can generate genuine multipartite entanglement and we certify the entanglement with the use of suitably tailored entanglement witnesses.
Similar content being viewed by others
Introduction
Since the seminal proposal by Knill, Laflamme and Milburn1 of an all-optical scalable quantum computing architecture, the field of linear optical quantum computing has experienced immense growth and expansion2,3. Various elementary quantum gates for qubits encoded into states of single photons have been demonstrated4,5,6,7,8,9,10,11,12,13,14,15,16, the optical quantum logic circuits have been miniaturized and integrated on a photonic chip17,18,19,20, and alternative more efficient approaches to all-optical quantum computing such as utilization of photonic cluster states21,22 have been developed. The number of optical photons which can be simultaneously generated and coherently processed has also increased in time23,24,25 up to the very recent record of 10 photons26. However, further scaling is largely prevented by the probabilistic nature of current sources of photons based on spontaneous parametric down-conversion, and deterministic single-photon sources of sufficient quality are not yet fully available despite recent significant progresses27,28,29.
Instead of increasing the number of photons one could exploit multiple degrees of freedom to encode several qubits in state of a single photon30. Although the total number of optical modes then increases exponentially with the number of qubits, this approach may nevertheless prove very useful for development of specific small-scale optical quantum circuits that can find applications, e.g., in nodes of optical quantum communication networks. Important examples of the simultaneous exploitation of several degrees of freedom of single photons for encoding and processing quantum information include generation of hyper-entangled photon pairs31, superdense quantum teleportation32, design of certain linear optical quantum logic gates14, and implementation of random quantum walks33,34,35.
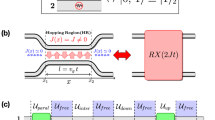
In this work, we exploit the polarization and path degrees of freedom to encode two qubits into a single photon and construct a two-photon four-qubit linear optical quantum logic circuit, which represents an important step beyond the previous implementations of two-4,5,6,7,8,9,10,11,13 and three-qubit14,15,16 linear optical quantum gates. The implemented quantum logic circuit is illustrated in Fig. 1(a). It combines several two-qubit quantum controlled-rotation gates, single-qubit gates, and a four-qubit generalized controlled-Z gate, which flips the sign of the state only if all four qubits are in the computational state |1〉,
(a) Scheme of the implemented quantum logic circuit. (b) Experimental setup. The central four-qubit C3Z gate is implemented by two-photon interference on a partially polarizing beam splitter PPBS1 followed by two additional PPBSs which serve as partial polarization filters. Notice that only the left and lower beams overlap and interfere on PPBS1. Single-qubit unitary gates Uj are implemented by a sequence of a rotated half-wave plate HWP and quarter-wave plate QWP which address both paths in a Mach-Zehnder interferometer formed by two calcite beam displacers BD. The two-qubit controlled rotation gates CRj are realized by a rotated HWP which is inserted only in one arm of the interferometer. Single-qubit phase gates Vk are achieved by tilting a glass plate GP inserted in one of the interferometer arms. The output states of photons are analyzed and detected with the help of wave plates, polarizing beam splitters PBS and avalanche photodiodes APD.

Here I denotes the identity operator on Hilbert space of four qubits. In our implementation, the qubits 1 and 2 are encoded into the polarization and path of the signal photon, respectively, while qubits 3 and 4 are similarly encoded into polarization and path of the idler photon. The two-qubit controlled-rotation gates applied to polarization and path qubits supported by the same photon can be implemented deterministically, while the core four-qubit C3Z gate is probabilistic, with theoretical success probability of  .
.
The four-qubit quantum logic circuit is a complex device, and its complete experimental characterization would require determination of 216−1 = 65535 parameters. Here we employ Hofmann fidelity bounds15,36 and Monte Carlo sampling techniques37,38 to efficiently characterize the performance of the quantum logic circuit. Our scheme provides a suitable platform for testing and illustrating the usefulness of these methods, which can also serve for efficient evaluation of other kinds of multi-qubit quantum gates. We find that the fidelity  of the four-qubit C3Z gate lies in the interval
of the four-qubit C3Z gate lies in the interval  and the Monte Carlo sampling provides an explicit fidelity estimate
and the Monte Carlo sampling provides an explicit fidelity estimate  . We show that our device can generate four-qubit GHZ-type entangled state whose fidelity with the ideal state and purity exceed 90%. Moreover, using suitable entanglement witnesses we verify that the generated state exhibits genuine four-partite entanglement. The developed scheme combining two crossed inherently stable optical interferometers provides a promising configuration for design of even more complex linear-optical quantum information processing devices.
. We show that our device can generate four-qubit GHZ-type entangled state whose fidelity with the ideal state and purity exceed 90%. Moreover, using suitable entanglement witnesses we verify that the generated state exhibits genuine four-partite entanglement. The developed scheme combining two crossed inherently stable optical interferometers provides a promising configuration for design of even more complex linear-optical quantum information processing devices.
Results
Experimental setup
In our experiment, a pair of time correlated orthogonally polarized photons at wavelength 810 nm is generated by spontaneous parametric down-conversion in a type-II nonlinear crystal pumped by a cw laser diode. The signal and idler photons are spatially separated at a polarizing beam splitter and injected into the two input ports of the interferometric setup which is depicted in Fig. 1(b) and consists of two crossed Mach-Zehnder interferometers formed by calcite beam displacers14,15. Each photon from the pair carries two qubits encoded into its polarization and path degrees of freedom. The horizontal and vertical polarizations of the photon represent the computational states |0〉 and |1〉 of the polarization qubit, respectively. Similarly, propagation in the displaced and straight arm of a Mach-Zehnder interferometer represents computational states |0〉 and |1〉 of the path qubit.
Path qubits are initially prepared in polarization encoding using combination of half-wave plate (HWP) and a quarter-wave plate (QWP) and subsequently converted into path encoding using a polarizing beam displacer (BD). The polarization-to-path conversion produces path-polarization entangled states. We can disentangle the state using a HWP that addresses only the straight arm of the interferometer. The action of this HWP rotated at 45° can be regarded as a quantum CNOT gate acting on the spatial control and polarization target qubits. Arbitrary polarization qubits can be prepared by an additional pair of HWP and QWP plates affecting both arms of the interferometer. The output state analysis blocks are counterparts of the preparation blocks, operating in a similar way and consisting of the same elements up to the final polarizing beam splitters and avalanche photodiodes. We can project the output photons onto an arbitrary product four-qubit state, and with suitable rotations of the HWPs addressing only the displaced arms of the interferometers we can also perform projections onto products of various two-qubit entangled states. The electronic signal from the avalanche photodiodes is processed by coincidence logic, and the number of coincidences detected during the measurement time is stored in a computer.
The core part of our linear optical quantum logic circuit consists of two-photon interference on the central partially polarizing beam splitter PPBS1. Implementation of the four-qubit C3Z gate requires that the two photons interfere only if their path qubits are both in the state |1〉, i.e. if they both propagate in the straight interferometer arms. To avoid interference of photons propagating in the displaced arms of the interferometers, we introduce different transverse separations of the interferometer arms for the two interferometers. Specifically, the beams are separated by 4 mm and 6 mm in the signal and idler interferometers, respectively, and the optical beams have diameter of 2 mm. The beams are adjusted such that the photons propagating in the straight arms perfectly overlap, while the photons propagating in the displaced arms are mutually transversally shifted and do not overlap on PPBS1. The nominal reflectances of PPBS1 read RH = 0 and RV = 2/3 for horizontally and vertically polarized photons, respectively. The other two partially polarizing beam splitters have inverted reflectances RH = 2/3 and RV = 0 so that the combinations of PPBS1 & PPBS2 and PPBS1 & PPBS3 form polarization insensitive gray filters with overall transmittance 1/3.
The above described optical design ensures that the conditional π-phase shift induced by the two-photon interference on PPBS1 occurs if and only if all four qubits are in the logical state |1〉. The physical principle of the conditional phase shift is the same as for the two-qubit linear optical quantum CZ gate demonstrated in Refs 7, 8, 9. The gate operates in the coincidence basis, its success is heralded by detection of a single photon in each output port of the gate, and the theoretical success probability of the four-qubit C3Z gate is  . The Mach-Zehnder interferometers formed by beam displacers are inherently stable and this stability is preserved even for the present configuration with two crossed interferometers. We observed that the whole setup is passively stable on the time scale of hours, which enables detailed and comprehensive characterization of the implemented quantum logic circuit.
. The Mach-Zehnder interferometers formed by beam displacers are inherently stable and this stability is preserved even for the present configuration with two crossed interferometers. We observed that the whole setup is passively stable on the time scale of hours, which enables detailed and comprehensive characterization of the implemented quantum logic circuit.
Experimental characterization of the four-qubit quantum C3Z gate
As illustrated in Fig. 2, the four-qubit C3Z gate, which is a central part of our linear optical quantum logic circuit, is equivalent to a four-qubit Toffoli gate up to local single-qubit Hadamard transforms on the target qubit. For each of the four choices of the target qubit we have measured the truth table of the resulting Toffoli gate, which illustrates its performance in the computational basis. The Hadamard transforms on the target qubit were implemented with the use of wave plates, which can be equivalently seen as probing the four-qubit CZ gate with a product state consisting of three control qubits prepared in the computational basis states |0〉, |1〉 and one target qubit prepared in the superposition basis state  . At the output of the four-qubit C3Z gate, the three control qubits are measured in the computational basis while the target qubit is measured in the superposition basis. The experimentally determined truth tables are shown in Fig. 2. The truth tables of all four Toffoli gates clearly show the expected bit flip of the target qubit conditional on all control qubits being prepared in the computational basis state |1〉.
. At the output of the four-qubit C3Z gate, the three control qubits are measured in the computational basis while the target qubit is measured in the superposition basis. The experimentally determined truth tables are shown in Fig. 2. The truth tables of all four Toffoli gates clearly show the expected bit flip of the target qubit conditional on all control qubits being prepared in the computational basis state |1〉.
Experimentally determined truth tables of the four-qubit quantum Toffoli gates.
The quantum logic circuits in each case indicate which qubit is the target qubit, and they also illustrate that each Toffoli gate is equivalent to a suitable combination of the C3Z gate and two single-qubit Hadamard gates.
We now specify in more detail the quantities plotted in Fig. 2. Let 
 denote the jth input four-qubit state when mth qubit is the target qubit. The corresponding output state is given by
denote the jth input four-qubit state when mth qubit is the target qubit. The corresponding output state is given by  where
where  is the four-qubit quantum operation actually implemented by our setup. Note that, due to various experimental imperfections,
is the four-qubit quantum operation actually implemented by our setup. Note that, due to various experimental imperfections,  can be a general trace-decreasing completely positive map. The output density matrices
can be a general trace-decreasing completely positive map. The output density matrices  are not normalized, and
are not normalized, and  is the probability of success of the gate for a given input state
is the probability of success of the gate for a given input state  . The truth tables depicted in Fig. 2 contain plots of the matrices
. The truth tables depicted in Fig. 2 contain plots of the matrices  of normalized overlaps of the actual output state
of normalized overlaps of the actual output state  with the ideal output states
with the ideal output states  produced by the perfect gate,
produced by the perfect gate,

In particular,  represents the output-state fidelity for input
represents the output-state fidelity for input  .
.
In the experiment, we measure the number of two-photon coincidences  for all combinations of input state
for all combinations of input state  and output projection onto
and output projection onto  . The measurement time is the same for all settings and set to 10 s. The normalized overlaps (2) are then estimated from the experimental data according to15
. The measurement time is the same for all settings and set to 10 s. The normalized overlaps (2) are then estimated from the experimental data according to15

For perfect albeit probabilistic implementation of a unitary gate, the success probabilities  should be constant and independent on the input state. To assess the behaviour of
should be constant and independent on the input state. To assess the behaviour of  for our implementation, we plot in Fig. 3 the total number of detected two-photon coincidences
for our implementation, we plot in Fig. 3 the total number of detected two-photon coincidences  for each of the 64 considered input states
for each of the 64 considered input states  . The variations of
. The variations of  visible in the figure are partly caused by the Poissonian fluctuations of the number of emitted photon pairs. To compare the observed behaviour of
visible in the figure are partly caused by the Poissonian fluctuations of the number of emitted photon pairs. To compare the observed behaviour of  with Poissonian statistics, we use the data plotted in Fig. 3 to estimate the variance
with Poissonian statistics, we use the data plotted in Fig. 3 to estimate the variance  of
of  and compare it with the variance of a Poissonian distribution with the same mean number of coincidences
and compare it with the variance of a Poissonian distribution with the same mean number of coincidences  . We obtain
. We obtain  and VD = 30338. This corresponds to relative fluctuations of
and VD = 30338. This corresponds to relative fluctuations of  of 8% while the corresponding relative Poissonian fluctuations would be about 2% (one relative standard deviation). This indicates that due to the various technical imperfections our implementation of the C3Z gate introduces slight dependence of
of 8% while the corresponding relative Poissonian fluctuations would be about 2% (one relative standard deviation). This indicates that due to the various technical imperfections our implementation of the C3Z gate introduces slight dependence of  on the input state.
on the input state.
Total number of detected two-photon coincidences  is plotted for the 64 input states
is plotted for the 64 input states  which were utilized in determination of the truth tables of the four-qubit Toffoli gates in Fig. 2.
which were utilized in determination of the truth tables of the four-qubit Toffoli gates in Fig. 2.
The data contained in the truth tables plotted in Fig. 2 can be used to derive a lower and upper bounds on the quantum process fidelity39,40 of the four-qubit C3Z gate,

Here χ and  denote the Choi matrices41,42 of the actually implemented and the ideal C3Z gate, respectively. It holds that
denote the Choi matrices41,42 of the actually implemented and the ideal C3Z gate, respectively. It holds that  , where
, where

is a maximally entangled state of 8 qubits. For each choice of the target qubit m in Fig. 2, we define a weighted average state fidelity Fm as

The four average state fidelities Fm determined from the truth tables of the four-qubit Toffoli gates plotted in Fig. 2 yield the following generalized Hofmann lower and upper bounds15,36 on the fidelity of the C3Z gate,

The experimentally determined average state fidelities read F1 = 0.943(1), F2 = 0.952(1), F3 = 0.944(1), and F4 = 0.955(1), which documents the very good performance of the gate. The statistical uncertainties of the fidelity estimates were obtained by error propagation assuming Poissonian statistics of the measured coincidence counts. If we insert these data into Eq. (7), we get  . An experimentally appealing property of these fidelity bounds is that they can be determined by measuring fidelities of multiqubit output product states obtained from input product states. Therefore, neither preparation of entangled states nor measurements in an entangled basis are required. However, the resulting lower bound on
. An experimentally appealing property of these fidelity bounds is that they can be determined by measuring fidelities of multiqubit output product states obtained from input product states. Therefore, neither preparation of entangled states nor measurements in an entangled basis are required. However, the resulting lower bound on  is rather loose.
is rather loose.
To obtain a better and tighter lower bound on  we have experimentally determined the original Hofmann fidelity bound36, which is given by average state fidelities
we have experimentally determined the original Hofmann fidelity bound36, which is given by average state fidelities  and
and  for two mutually unbiased bases. In particular, it holds that
for two mutually unbiased bases. In particular, it holds that

In our experiment, we construct the two mutually unbiased bases by preparing the polarization and path qubits of one photon in the computational basis states |0〉, |1〉 and the polarization and path qubits of the other photon in the superposition basis states |+〉, |−〉. The average state fidelities  are defined similarly as Fm. However, the determination of the corresponding output state fidelities
are defined similarly as Fm. However, the determination of the corresponding output state fidelities  now requires measurements in entangled basis, since the C3Z gate maps some of the input states onto entangled output states. For instance,
now requires measurements in entangled basis, since the C3Z gate maps some of the input states onto entangled output states. For instance,

Fortunately, the output state fidelities  can be directly measured with our quantum logic circuit, because we can set the two controlled-rotation gates CR3 and CR4 in Fig. 1 to CNOT gates and perform measurements in the basis of maximally entangled Bell states. The experimentally determined output state fidelities
can be directly measured with our quantum logic circuit, because we can set the two controlled-rotation gates CR3 and CR4 in Fig. 1 to CNOT gates and perform measurements in the basis of maximally entangled Bell states. The experimentally determined output state fidelities  are plotted in Fig. 4 and the resulting average state fidelities read
are plotted in Fig. 4 and the resulting average state fidelities read  and
and  . Consequently, we obtain the following bounds on the fidelity of the C3Z gate,
. Consequently, we obtain the following bounds on the fidelity of the C3Z gate,

With a rather small number of measurements we have thus successfully confirmed the high-quality performance of our multiqubit quantum logic circuit and we have constrained the fidelity of the four-qubit quantum controlled-Z gate into a narrow interval.
Preparation of four-qubit entangled state
We next investigate the ability of the C3Z gate to generate genuine multipartite entangled states from input product states. Specifically, we consider the input state |++++〉 which is transformed by the C3Z gate into an entangled state that belongs to the family of four-qubit GHZ states,

We have performed a tomographically overcomplete set of measurements on the generated four-qubit state and we have reconstructed its density matrix ρ+ from the experimental data using the Maximum Likelihood estimation procedure43,44. The resulting density matrix is plotted in Fig. 5. We can characterize the generated entangled state by its purity  and fidelity
and fidelity  . Using the experimentally determined ρ+ we obtain F+ = 0.942(2) and
. Using the experimentally determined ρ+ we obtain F+ = 0.942(2) and  which demonstrates high quality of the generated state.
which demonstrates high quality of the generated state.
In order to certify that the experimentally prepared four-qubit state exhibits genuine multipartite entanglement, we utilize a suitable entanglement witness45,46,47. We recall that a multipartite quantum state exhibits a genuine multipartite entanglement if it cannot be written as a mixture of biseparable states. Consider first a maximally entangled GHZ state

where  and
and  denote two orthogonal single-qubit states. An optimal projector entanglement witness48,49 for the state (12) is given by
denote two orthogonal single-qubit states. An optimal projector entanglement witness48,49 for the state (12) is given by

A genuine four-partite entanglement of a state ρ is certified when  , i.e. when the fidelity of the state with the maximally entangled GHZ state (12) exceeds
, i.e. when the fidelity of the state with the maximally entangled GHZ state (12) exceeds  . The overlap
. The overlap

is maximized for  , and at this point
, and at this point  . This shows that the standard GHZ witness (13) is capable to detect multipartite entanglement of the four-qubit state
. This shows that the standard GHZ witness (13) is capable to detect multipartite entanglement of the four-qubit state  . For the experimentally determined state ρ+ we find that the witness is minimized at
. For the experimentally determined state ρ+ we find that the witness is minimized at  , in excellent agreement with theoretical expectations. At this optimal point we get
, in excellent agreement with theoretical expectations. At this optimal point we get  which confirms that the experimentally generated state exhibits genuine multipartite entanglement.
which confirms that the experimentally generated state exhibits genuine multipartite entanglement.
To complete our analysis we also present two alternative constructions of witnesses which can detect multipartite entanglement of the state  . Our first construction is based on the observation that the four-qubit state
. Our first construction is based on the observation that the four-qubit state  can be transformed onto the canonical GHZ state
can be transformed onto the canonical GHZ state  by local single-qubit operations. In particular, we have
by local single-qubit operations. In particular, we have

where

denotes a single-qubit quantum filter. Since local single-qubit quantum filters map biseparable states onto biseparable states, a filtered state  , where
, where  , exhibits genuine multipartite entanglement only if the original state ρ also exhibits genuine multipartite entanglement. Starting from the optimal witness (13) for the canonical GHZ state
, exhibits genuine multipartite entanglement only if the original state ρ also exhibits genuine multipartite entanglement. Starting from the optimal witness (13) for the canonical GHZ state  , and considering its application to the filtered state
, and considering its application to the filtered state  , we arrive at the following witness for the original state ρ,
, we arrive at the following witness for the original state ρ,

For the experimentally generated four-qubit state ρ+ we get  , while for the ideal pure state (11) one has
, while for the ideal pure state (11) one has  . In our second approach we utilize a projector witness of the form
. In our second approach we utilize a projector witness of the form

The proof that this is an optimal projector witness for the state  is provided in the Methods section. For the experimentally reconstructed state we obtain
is provided in the Methods section. For the experimentally reconstructed state we obtain  .
.
A comparison of the three above discussed entanglement witnesses is provided in Table 1. Besides the mean values of the three witnesses, the table also shows the significance of the entanglement test50 defined as  , where ΔW is the standard deviation quantifying statistical uncertainty of 〈W〉. Moreover, the table also displays the maximum tolerable fraction of white noise pmax for which the witness still detects entanglement of a mixed state
, where ΔW is the standard deviation quantifying statistical uncertainty of 〈W〉. Moreover, the table also displays the maximum tolerable fraction of white noise pmax for which the witness still detects entanglement of a mixed state  . We can see that WGHZ is the optimal witness as it achieves the highest significance
. We can see that WGHZ is the optimal witness as it achieves the highest significance  and also it can tolerate more white noise than the other two witnesses.
and also it can tolerate more white noise than the other two witnesses.
 .
.Monte-Carlo sampling of quantum gate fidelity
The four-qubit quantum C3Z gate represents an interesting nontrivial device for testing techniques devised for efficient characterization of multiqubit quantum operations37,38,51,52,53,54,55,56,57. The Hofmann bound36 utilized in the previous part of our work can be considered as an example of such efficient partial characterization technique, but it should be noted that the number of measurement settings required for determination of the Hofmann bounds still scales exponentially with the number of qubits N. This exponential bottleneck can be avoided by the Monte Carlo sampling of quantum gate fidelity37,38,51,52. The main feature of this technique is that the number of measurement settings depends on the required uncertainty of the fidelity estimate but not on the dimension of the Hilbert space.
Here we apply the Monte Carlo sampling to determine the fidelity of the four-qubit quantum C3Z gate given by Eq. (4). The first step is to express the quantum process matrix  of the ideal C3Z gate as a linear combination of 8-fold tensor products of single-qubit Pauli operators σX, σY, σZ and σ0 = I. We find that the expansion contains altogether 1936 different tensor products,
of the ideal C3Z gate as a linear combination of 8-fold tensor products of single-qubit Pauli operators σX, σY, σZ and σ0 = I. We find that the expansion contains altogether 1936 different tensor products,

where  are real constants,
are real constants,

 , and each parameter j labels a specific 8-fold tensor product (20). Since in our experiment we sequentially probe the quantum gate by various input states, we rewrite the expansion (19) as a linear combination of projectors onto pure product states. For this purpose, we express each of the three Pauli matrices σX, σY and σZ as a difference of projectors onto their +1 and −1 eigenstates and, similarly, we explicitly write
, and each parameter j labels a specific 8-fold tensor product (20). Since in our experiment we sequentially probe the quantum gate by various input states, we rewrite the expansion (19) as a linear combination of projectors onto pure product states. For this purpose, we express each of the three Pauli matrices σX, σY and σZ as a difference of projectors onto their +1 and −1 eigenstates and, similarly, we explicitly write  . After some algebra, we arrive at the expansion
. After some algebra, we arrive at the expansion

where  and
and  are positive coefficients,
are positive coefficients,

and each of the operators  and
and  is a projector onto one of the eigenstates of σX, σY or σZ. The total number of terms in the expansion (21) reads N+ = 22416 and N− = 22400.
is a projector onto one of the eigenstates of σX, σY or σZ. The total number of terms in the expansion (21) reads N+ = 22416 and N− = 22400.
As a final preparatory step we introduce two probability distributions

where

The Monte Carlo sampling proceeds as follows. We randomly generate a list of M+ labels cm in the range [1, N+] drawn from a distribution  , and we also generate a list of M− labels dm in the range [1, N−] drawn from the distribution
, and we also generate a list of M− labels dm in the range [1, N−] drawn from the distribution  . Next, we experimentally determine the mean values of the randomly chosen projectors
. Next, we experimentally determine the mean values of the randomly chosen projectors  and
and  ,
,

Practically, each of these terms can be measured by preparing a suitable four-qubit input product state and by performing a projection onto a suitable four-qubit product state at the output. Since the investigated optical quantum gate is probabilistic, we also need to carry out a reference measurement to determine the normalization factor  . Generally, this normalization factor could be also estimated by Monte Carlo sampling. However, for the considered four-qubit gate it is possible to obtain the required reference by performing a complete measurement in the computational basis, which involves M0 = 28 measurement settings. The gate fidelity is then estimated according to the formula
. Generally, this normalization factor could be also estimated by Monte Carlo sampling. However, for the considered four-qubit gate it is possible to obtain the required reference by performing a complete measurement in the computational basis, which involves M0 = 28 measurement settings. The gate fidelity is then estimated according to the formula

To assess the systematic error of gate fidelity estimation due to the finite number of samples M+ and M−, we assume perfect gate implementation,  , and neglect the statistical uncertainty of
, and neglect the statistical uncertainty of  and
and  . The systematic error of fidelity estimation due to finite number of samples can then be expressed as
. The systematic error of fidelity estimation due to finite number of samples can then be expressed as

where

and  is defined similarly. For a fixed total number of samples
is defined similarly. For a fixed total number of samples  we can minimize the systematic error (27) by optimizing the number of samples M+ and M−. This yields
we can minimize the systematic error (27) by optimizing the number of samples M+ and M−. This yields

On inserting these optimal values back into Eq. (27) we obtain

Numerically, we get

and

This indicates that the optimal sampling strategy is strongly unbalanced, with almost 90% of samples used to estimate the positive terms in the expansion (21) and only about 10% of samples is allocated to estimate the negative terms in that expansion. Formula (32) provides an explicit quantification of the systematic error of the Monte Carlo sampling procedure. To reduce the sampling error below 1% (as quantified by one standard deviation  ), at least 2.5 × 104 samples are required, which is comparable with the total number of terms N+ and N− in the expansion (21).
), at least 2.5 × 104 samples are required, which is comparable with the total number of terms N+ and N− in the expansion (21).
We have experimentally probed the performance of the Monte Carlo sampling procedure for our linear optical four-qubit quantum gate. We have generated the random list of MT = 1100 measurement settings, measured the number of coincidences for a fixed time interval for all these settings, and we have also performed the measurements in the computational basis required for normalization. From these data we have determined the mean values (25) and obtained an estimate of the gate fidelity FMC. We have repeated this procedure 15 times and the resulting fidelity estimates are plotted in Fig. 6. We characterize the ensemble of fidelity estimates by its mean  and standard deviation ΔFMC = 0.042. This is consistent with the systematic error 0.048 predicted by formula (32) and the statistical error 0.011 due to Poissonian statistics of the coincidence events. The mean fidelity
and standard deviation ΔFMC = 0.042. This is consistent with the systematic error 0.048 predicted by formula (32) and the statistical error 0.011 due to Poissonian statistics of the coincidence events. The mean fidelity  is in excellent agreement with the lower and upper Hofmann bounds (10). The uncertainty of
is in excellent agreement with the lower and upper Hofmann bounds (10). The uncertainty of  can be estimated as
can be estimated as  , where K = 15 is the number of repetitions of the Monte Carlo sampling procedure.
, where K = 15 is the number of repetitions of the Monte Carlo sampling procedure.
Monte Carlo estimates FMC of fidelity of the experimentally implemented C3Z gate.
Each estimate was obtained from MT = 1100 samples and the whole sampling procedure was independently repeated 15 times to obtain an ensemble of fidelities. The error bars indicate statistical errors due to finite number of two-photon coincidence counts.
We used the 16500 measured coincidences to reconstruct the implemented quantum process using the Maximum Likelihood estimation procedure. Since the data are tomographically incomplete, we have used 20 random operators at the beginning of the iterative reconstruction algorithm to check that the reconstruction always yields the same quantum process fidelity  which lies inside the previously estimated boundaries.
which lies inside the previously estimated boundaries.
Discussion
In summary, we have experimentally demonstrated and characterized a four-qubit optical quantum logic circuit whose core is formed by a four-qubit C3Z gate. Our scheme exploits encoding of two qubits into polarization and path degrees of single photons and involves two crossed inherently stable interferometers. Our setup is passively stable on the time scale of hours which provided sufficient time for a comprehensive experimental characterization of the optical quantum logic circuit. We have verified high-fidelity performance of the central four-qubit C3Z gate and we have demonstrated that it can generate genuine multipartite entanglement. Our work illustrates that Monte Carlo sampling and Hofmann fidelity bounds are useful methods of characterization of complex multi-qubit quantum devices. The applicability of these methods is rather universal, and they can be used to efficiently characterize quantum logic gates and circuits implemented on various physical systems.
The implemented scheme combining two crossed interferometers is very flexible and with suitable modifications it may enable also realization of other quantum operations such as creation of superposition of unknown photonic quantum states and quantum Fredkin gate58. Moreover, by using additional calcite beam displacers, one could increase the number of paths in each interferometer which would enable experiments with multivalued quantum logic circuits where path degree of each photon supports a qudit instead of a qubit.
Methods
Optimal Projector witness for |Ψ4+〉
Here we construct the optimal projector witness

for the state  defined in Eq. (11). To optimize the witness (33), the coefficient α should be equal to the maximum overlap of the state
defined in Eq. (11). To optimize the witness (33), the coefficient α should be equal to the maximum overlap of the state  with a biseparable state. Since the set of biseparable states is convex and the state
with a biseparable state. Since the set of biseparable states is convex and the state  is invariant with respect to permutations of qubits, it suffices to maximize the overlap with pure biseparable states
is invariant with respect to permutations of qubits, it suffices to maximize the overlap with pure biseparable states  and
and  . Here the subscripts label the four qubits, so for instance |σ〉1 is a single-qubit state and
. Here the subscripts label the four qubits, so for instance |σ〉1 is a single-qubit state and  is a two-qubit state. We introduce explicit parametrization of these two states,
is a two-qubit state. We introduce explicit parametrization of these two states,

with the normalization conditions  and
and  . It holds that
. It holds that

The maximization of  can be performed in a similar manner. We find that the optimal state
can be performed in a similar manner. We find that the optimal state  reads
reads

and the maximization of the overlap amounts to maximization of the function

The maximum is achieved at  and we arrive at
and we arrive at

We thus find that  and the optimal projector witness for the state
and the optimal projector witness for the state  reads
reads  .
.
Additional Information
How to cite this article: Stárek, R. et al. Experimental investigation of a four-qubit linear-optical quantum logic circuit. Sci. Rep. 6, 33475; doi: 10.1038/srep33475 (2016).
References
Knill, E., Laflamme, R. & Milburn, G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001).
Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135–174 (2007).
Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. Nat. Phys. 8, 285–291 (2012).
O’Brien, J. L., Pryde, G. J., White, A. G., Ralph, T. C. & Branning, D. Demonstration of an all-optical quantum controlled-not gate. Nature 426, 264–267 (2003).
Gasparoni, S., Pan, J.-W., Walther, P., Rudolph, T. & Zeilinger, A. Realization of a photonic controlled-not gate sufficient for quantum computation. Phys. Rev. Lett. 93, 020504 (2004).
Zhao, Z. et al. Experimental demonstration of a nondestructive controlled-not quantum gate for two independent photon qubits. Phys. Rev. Lett. 94, 030501 (2005).
Okamoto, R., Hofmann, H. F., Takeuchi, S. & Sasaki, K. Demonstration of an optical quantum controlled-not gate without path interference. Phys. Rev. Lett. 95, 210506 (2005).
Langford, N. K. et al. Demonstration of a simple entangling optical gate and its use in bell-state analysis. Phys. Rev. Lett. 95, 210504 (2005).
Kiesel, N., Schmid, C., Weber, U., Ursin, R. & Weinfurter, H. Linear optics controlled-phase gate made simple. Phys. Rev. Lett. 95, 210505 (2005).
Černoch, A., Soubusta, J., Bartůšková, L., Dušek, M. & Fiurášek, J. Experimental realization of linear-optical partial swap gates. Phys. Rev. Lett. 100, 180501 (2008).
Gao, W.-B. et al. Teleportation-based realization of an optical quantum two-qubit entangling gate. Proceedings of the National Academy of Sciences 107, 20869–20874 (2010).
Lemr, K. et al. Experimental implementation of the optimal linear-optical controlled phase gate. Phys. Rev. Lett. 106, 013602 (2011).
Zhou, X.-Q. et al. Adding control to arbitrary unknown quantum operations. Nat. Commun. 2, 413 (2011).
Lanyon, B. P. et al. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 5, 134–140 (2009).
Mičuda, M. et al. Efficient experimental estimation of fidelity of linear optical quantum Toffoli gate. Phys. Rev. Lett. 111, 160407 (2013).
Patel, R. B., Ho, J., Ferreyrol, F., Ralph, T. C. & Pryde, G. J. A quantum Fredkin gate. Science Advances 2 (2016).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & O’Brien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Crespi, A. et al. Integrated photonic quantum gates for polarization qubits. Nat. Commun. 2, 566 (2011).
Metcalf, B. J. et al. Quantum teleportation on a photonic chip. Nat. Photon. 8, 770–774 (2014).
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).
Nielsen, M. A. Optical quantum computation using cluster states. Phys. Rev. Lett. 93, 040503 (2004).
Walther, P. et al. Experimental one-way quantum computing. Nature 434, 169–176 (2005).
Lu, C.-Y. et al. Experimental entanglement of six photons in graph states. Nat. Phys. 3, 91–95 (2007).
Wieczorek, W. et al. Experimental entanglement of a six-photon symmetric Dicke state. Phys. Rev. Lett. 103, 020504 (2009).
Yao, X.-C. et al. Observation of eight-photon entanglement. Nat. Photon. 6, 225–228 (2012).
Wang, X.-L. et al. Experimental ten-photon entanglement. ArXiv e-prints 1605.08547 (2016).
Eisaman, M. D., Fan, J., Migdall, A. & Polyakov, S. V. Invited review article: Single-photon sources and detectors. Review of Scientific Instruments 82 (2011).
Lodahl, P., Mahmoodian, S. & Stobbe, S. Interfacing single photons and single quantum dots with photonic nanostructures. Rev. Mod. Phys. 87, 347–400 (2015).
Schwartz, I. et al. Deterministic generation of a cluster state of entangled photons. ArXiv e-prints 1606.07492 (2016).
Cerf, N. J., Adami, C. & Kwiat, P. G. Optical simulation of quantum logic. Phys. Rev. A 57, R1477–R1480 (1998).
Barreiro, J. T., Langford, N. K., Peters, N. A. & Kwiat, P. G. Generation of hyperentangled photon pairs. Phys. Rev. Lett. 95, 260501 (2005).
Graham, T. M., Bernstein, H. J., Wei, T.-C., Junge, M. & Kwiat, P. G. Superdense teleportation using hyperentangled photons. Nat. Commun. 6, 7185 (2015).
Schreiber, A. et al. Photons walking the line: A quantum walk with adjustable coin operations. Phys. Rev. Lett. 104, 050502 (2010).
Schreiber, A. et al. A 2D quantum walk simulation of two-particle dynamics. Science 336, 55–58 (2012).
Sansoni, L. et al. Two-particle bosonic-fermionic quantum walk via integrated photonics. Phys. Rev. Lett. 108, 010502 (2012).
Hofmann, H. F. Complementary classical fidelities as an efficient criterion for the evaluation of experimentally realized quantum operations. Phys. Rev. Lett. 94, 160504 (2005).
Flammia, S. T. & Liu, Y.-K. Direct fidelity estimation from few Pauli measurements. Phys. Rev. Lett. 106, 230501 (2011).
da Silva, M. P., Landon-Cardinal, O. & Poulin, D. Practical characterization of quantum devices without tomography. Phys. Rev. Lett. 107, 210404 (2011).
Schumacher, B. Sending entanglement through noisy quantum channels. Phys. Rev. A 54, 2614–2628 (1996).
Horodecki, M., Horodecki, P. & Horodecki, R. General teleportation channel, singlet fraction, and quasidistillation. Phys. Rev. A 60, 1888–1898 (1999).
Jamiołkowski, A. An effective method of investigation of positive maps on the set of positive definite operators. Reports on Mathematical Physics 5, 415–424 (1974).
Choi, M.-D. Completely positive linear maps on complex matrices. Linear Algebra and its Applications 10, 285–290 (1975).
Hradil, Z. Quantum-state estimation. Phys. Rev. A 55, R1561–R1564 (1997).
Ježek, M., Fiurášek, J. & Hradil, Z. Quantum inference of states and processes. Phys. Rev. A 68, 012305 (2003).
Horodecki, M., Horodecki, P. & Horodecki, R. Separability of mixed states: necessary and sufficient conditions. Physics Letters A 223, 1–8 (1996).
Terhal, B. M. Bell inequalities and the separability criterion. Physics Letters A 271, 319- 326 (2000).
Lewenstein, M., Kraus, B., Cirac, J. I. & Horodecki, P. Optimization of entanglement witnesses. Phys. Rev. A 62, 052310 (2000).
Tóth, G. & Gühne, O. Detecting genuine multipartite entanglement with two local measurements. Phys. Rev. Lett. 94, 060501 (2005).
Jungnitsch, B., Moroder, T. & Gühne, O. Entanglement witnesses for graph states: General theory and examples. Phys. Rev. A 84, 032310 (2011).
Jungnitsch, B. et al. Increasing the statistical significance of entanglement detection in experiments. Phys. Rev. Lett. 104, 210401 (2010).
Steffen, L., da Silva, M. P., Fedorov, A., Baur, M. & Wallraff, A. Experimental Monte Carlo quantum process certification. Phys. Rev. Lett. 108, 260506 (2012).
Mičuda, M. et al. Tomographic characterization of a linear optical quantum Toffoli gate. Phys. Rev. A 92, 032312 (2015).
Gross, D., Liu, Y.-K., Flammia, S. T., Becker, S. & Eisert, J. Quantum state tomography via compressed sensing. Phys. Rev. Lett. 105, 150401 (2010).
Shabani, A. et al. Efficient measurement of quantum dynamics via compressive sensing. Phys. Rev. Lett. 106, 100401 (2011).
Emerson, J. et al. Symmetrized characterization of noisy quantum processes. Science 317, 1893–1896 (2007).
Moussa, O., da Silva, M. P., Ryan, C. A. & Laflamme, R. Practical experimental certification of computational quantum gates using a twirling procedure. Phys. Rev. Lett. 109, 070504 (2012).
Lu, D. et al. Experimental estimation of average fidelity of a Clifford gate on a 7-qubit quantum processor. Phys. Rev. Lett. 114, 140505 (2015).
Hu, X.-M. et al. Experimental creation of superposition of unknown photonic quantum states. ArXiv e-prints (2016) 1605.02339.
Acknowledgements
This work was supported by the Czech Science Foundation (GA16-17314S). I.S. acknowledges support by Palacky University (IGA-PrF-2016-009).
Author information
Authors and Affiliations
Contributions
R.S. and M. Mičuda. designed the experimental setup and performed the experiment with contributions from I.S., M.J., and M. Miková, M.J. and M.D. supervised and coordinated the experiment. J.F. performed the theoretical calculations. J.F., R.S. and M. Mičuda. analyzed the experimental data and wrote the manuscript with input from all authors.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Stárek, R., Mičuda, M., Miková, M. et al. Experimental investigation of a four-qubit linear-optical quantum logic circuit. Sci Rep 6, 33475 (2016). https://doi.org/10.1038/srep33475
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep33475
- Springer Nature Limited
This article is cited by
-
Nondestructive detector for exchange symmetry of photonic qubits
npj Quantum Information (2018)


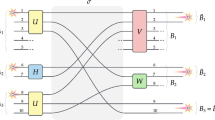





 for input states forming two mutually unbiased bases.
for input states forming two mutually unbiased bases.
