Abstract
Tsallis-q entanglement is a bipartite entanglement measure which is the generalization of entanglement of formation for q tending to 1. We first expand the range of q for the analytic formula of Tsallis-q entanglement. For  , we prove the monogamy relation in terms of the squared Tsallis-q entanglement for an arbitrary multi-qubit systems. It is shown that the multipartite entanglement indicator based on squared Tsallis-q entanglement still works well even when the indicator based on the squared concurrence loses its efficacy. We also show that the μ-th power of Tsallis-q entanglement satisfies the monogamy or polygamy inequalities for any three-qubit state.
, we prove the monogamy relation in terms of the squared Tsallis-q entanglement for an arbitrary multi-qubit systems. It is shown that the multipartite entanglement indicator based on squared Tsallis-q entanglement still works well even when the indicator based on the squared concurrence loses its efficacy. We also show that the μ-th power of Tsallis-q entanglement satisfies the monogamy or polygamy inequalities for any three-qubit state.
Similar content being viewed by others
Introduction
Quantum entanglement as a physics resource for quantum communication and quantum information processing has been the subject of many recent studies in recent years1,2,3,4,5,6,7. The study of quantum entanglement from various view points has been a very active area and has led to many interesting results. Monogamy of entanglement(MOE)8 is an interesting property discovered recently in the context of multi-qubit entanglement, which means that quantum entanglement cannot be shared freely in multi-qubit quantum systems. The bipartite monogamy inequality was first proposed and proved by Coffman, Kundu and Wootters(CKW) in a three-qubit system9, and it is also named as CKW inequality:

where  is the squared of concurrence between the pair i and j10. Later, the monogamy inequality was generalized into various entanglement measures such as continuous-variable entanglement11,12,13, squashed entanglement14,15,16, entanglement negativity17,18,19,20,21, Tsallis-q entanglement22,23, and Rényi-α entanglement24,25,26. The applications of monogamy relation include many fields of physics such as characterizing the entanglement structure in multipartite quantum systems27,28,29,30,31,32,33,34,35,36,37,38,39,40,41, the security proof in quantum cryptography42, the frustration effects observed in condensed matter physics43, and even black hole physics43,44,45,46,47,48. Originally, MOE was established in terms of the squared concurrence(SC). Analogously, Bai et al.49,50 have proved that the squared entanglement of formation(SEF) obeys the monogamy relation in arbitrary N-qubit mixed state. It should be noted that the entanglement of formation(EOF) itself does not satisfy the monogamy relation even for three-qubit pure states. The new monogamy relation in terms of SEF overcomes some flaws of the SC and can be used to detect all genuine multipartite entanglement for N-qubit systems.
is the squared of concurrence between the pair i and j10. Later, the monogamy inequality was generalized into various entanglement measures such as continuous-variable entanglement11,12,13, squashed entanglement14,15,16, entanglement negativity17,18,19,20,21, Tsallis-q entanglement22,23, and Rényi-α entanglement24,25,26. The applications of monogamy relation include many fields of physics such as characterizing the entanglement structure in multipartite quantum systems27,28,29,30,31,32,33,34,35,36,37,38,39,40,41, the security proof in quantum cryptography42, the frustration effects observed in condensed matter physics43, and even black hole physics43,44,45,46,47,48. Originally, MOE was established in terms of the squared concurrence(SC). Analogously, Bai et al.49,50 have proved that the squared entanglement of formation(SEF) obeys the monogamy relation in arbitrary N-qubit mixed state. It should be noted that the entanglement of formation(EOF) itself does not satisfy the monogamy relation even for three-qubit pure states. The new monogamy relation in terms of SEF overcomes some flaws of the SC and can be used to detect all genuine multipartite entanglement for N-qubit systems.
On the other hand, Tsallis-q entanglement is also a well-defined entanglement measure which is the generalization of EOF. For q tending to 1, the Tsallis-q entanglement converges to the EOF. A natural question is whether the monogamy relation can be generalized to Tsallis-q entanglement. In fact, Kim has derived a monogamy relation in terms of Tsallis-q entanglement22. However, the result in ref. 22 fails in including EOF as a special case and only holds for 2 ≤ q ≤ 3. In this paper we further consider the monogamy relation in terms of the squared Tsallis-q entanglement(STqE). Firstly we expand the range of q for the analytic formula of Tsallis-q entanglement. Then we prove a monogamy inequality of multi-qubit systems in terms of STqE in an arbitrary N-qubit mixed state for  , which covers the case of EOF as a special case. Finally, we show that the μ-th power of the Tsallis-q entanglement satisfies the monogamy inequalities for three-qubit state.
, which covers the case of EOF as a special case. Finally, we show that the μ-th power of the Tsallis-q entanglement satisfies the monogamy inequalities for three-qubit state.
Results
Analytic formula of Tsallis-q entanglement
Firstly we recall the definition of Tsallis-q entanglement introduced in ref. 22. For a bipartite pure state |ψ〉AB, the Tsallis-q entanglement is defined as

for any q > 0 and q ≠ 1, where ρA = trB|ψ〉AB〈ψ| is the reduced density matrix by tracing over the subsystem B. For the case when q tends to 1, Tq(ρ) converges to the von Neumann entropy, that is

For a bipartite mixed state ρAB, Tsallis-q entanglement is defined via the convex-roof extension

where the minimum is taken over all possible pure state decompositions of  .
.
In ref. 22, Kim has proved an analytic relationship between Tsallis-q entanglement and concurrence for 1 ≤ q ≤ 4 as follows

where the function gq(x) is defined as

According to the results in ref. 22, the analytic formula in Eq. (5) holds for any q such that gq(x) in Eq. (6) is monotonically increasing and convex. Next we shall generalize the range of q when the function gq(x) is convex and monotonically increasing with respect to x. The monotonicity and convexity of gq(x) follow from the nonnegativity of its first and second derivatives. After a direct calculation, we find that the first derivative of gq(x) with respect to x is always nonnegative for q ≥ 022. Kim has also proved the nonnegative of the second-order derivative gq(x) for 1 ≤ q ≤ 4. We can further consider the second-order derivative of gq(x) beyond the region 1 ≤ q ≤ 4. We first analyze the nonnegative region for the second-order derivative gq(x) for q ∈ (0, 1). Numerical calculation shows that under the condition ∂2Tq(C)/∂x2 = 0, the critical value of x increases monotonically with the parameter q. In Fig. 1(a), we plot the solution (x, q) to this critical condition, where for each fixed x there exists a value of q such that the second-order derivative of Tq(C) is zero. Because x varying monotonically with q, we should only consider the condition ∂2Tq(C)/∂x2 = 0 in the limit x → 1. When x = 1, we have

which gives the critical point  . When q > qc1, the second-order ∂2Tq/∂x2 is always nonnegative. For q ∈ (4, 5), we find that the value of x decreases monotonically with respect to q as shown in Fig. 1(b). In order to determine the critical point we should only consider the condition ∂2Tq/∂x2 = 0 in the limit x → 1. After direct calculation, we can obtain that the critical point
. When q > qc1, the second-order ∂2Tq/∂x2 is always nonnegative. For q ∈ (4, 5), we find that the value of x decreases monotonically with respect to q as shown in Fig. 1(b). In order to determine the critical point we should only consider the condition ∂2Tq/∂x2 = 0 in the limit x → 1. After direct calculation, we can obtain that the critical point  . When q < qc2, the second-order ∂2Tq/∂x2 is always nonnegative. Combining with the previous results in ref. 22, we get that the second derivative of gq(x) is always a nonnegative function for
. When q < qc2, the second-order ∂2Tq/∂x2 is always nonnegative. Combining with the previous results in ref. 22, we get that the second derivative of gq(x) is always a nonnegative function for  . Thus we have shown that the analytic formula of Tsallis-q entanglement in Eq. (5) holds for
. Thus we have shown that the analytic formula of Tsallis-q entanglement in Eq. (5) holds for  .
.
Monogamy inequalities for STqE in N-qubit systems
In the following we consider the monogamy properties of STqE. Using the results presented in Methods, we can prove the main result of this paper.
For an arbitrary N-qubit mixed state  , the squared Tsallis-q entanglement satisfies the monogamy relation
, the squared Tsallis-q entanglement satisfies the monogamy relation

where  quantifies the Tsallis-q entanglement in the partition A1|A2 ···An and
quantifies the Tsallis-q entanglement in the partition A1|A2 ···An and  quantifies the one in two-qubit subsystem A1Ai with the parameter
quantifies the one in two-qubit subsystem A1Ai with the parameter  .
.
For proving the above inequality, we first analyze an N-qubit pure state  . Under the partition A1|A2 ···An, we have
. Under the partition A1|A2 ···An, we have

where in the first inequality we have used the monogamy relation of squared concurrence  and the monotonically increasing property of
and the monotonically increasing property of  which has been proved in Methods, and the second inequality is due to the convex property of
which has been proved in Methods, and the second inequality is due to the convex property of  (The details for proving the convexity property can be seen from Methods).
(The details for proving the convexity property can be seen from Methods).
Next, we prove the monogamy relation for an N-qubit mixed state  . In this case, the formula of Tsallis-q entanglement cannot be applied to
. In this case, the formula of Tsallis-q entanglement cannot be applied to  since the subsystem A2 ···An is not a logic qubit in general. But we can still use the definition of Tsallis-q entanglement in Eq. (4). Thus, we have
since the subsystem A2 ···An is not a logic qubit in general. But we can still use the definition of Tsallis-q entanglement in Eq. (4). Thus, we have

where the minimum is taken over all possible pure state decompositions {pi, |ψi〉} of the mixed state  . Under the optimal decomposition
. Under the optimal decomposition  , we have
, we have

where in the second equality we have used the pure state formula of the Tsallis-q entanglement and taken the Tq(C) as a function of the concurrence C for  ; the third inequality is due to that Tq is a monotonically increasing and convex function of the concurrence for
; the third inequality is due to that Tq is a monotonically increasing and convex function of the concurrence for  ; the forth inequality is due to the convex property of concurrence for mixed state; and in the sixth and seventh inequalities we used the monotonically increasing and convex properties of
; the forth inequality is due to the convex property of concurrence for mixed state; and in the sixth and seventh inequalities we used the monotonically increasing and convex properties of  as a function of the squared concurrence for
as a function of the squared concurrence for  (The details for illustrating the property of STqE can be seen from Methods). Thus we have completed the proof of the monogamy inequalities for STqE in N-qubit systems.
(The details for illustrating the property of STqE can be seen from Methods). Thus we have completed the proof of the monogamy inequalities for STqE in N-qubit systems.
As an application of the established monogamy relation in Eq. (8), we can construct the multipartite entanglement indicator  to detect the genuine multipartite entanglement. We consider a three-qubit pure state
to detect the genuine multipartite entanglement. We consider a three-qubit pure state  , which is the superposition of a GHZ state and a W state with
, which is the superposition of a GHZ state and a W state with  and
and  . The three-tangle τ introduced in ref. 9 is defined as
. The three-tangle τ introduced in ref. 9 is defined as  . For the quantum state |ψ(p)〉, its three-tangle is
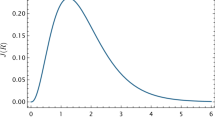
. For the quantum state |ψ(p)〉, its three-tangle is  which has two zero points at p1 = 0 and p2 ≈ 0.627. On the other hand, we can directly calculate the value of τq(|ψ(p)〉) since the Tsallis-q entanglement has an analytical formula for two-qubit quantum states. In Fig. 2 we plot the three-tangle and the indicator τq for the order q = 0.8, 1.1, 1.4. It is shown that the indicator τq is always positive for the different order q in contrast to the three-tangle τ having two zero points. Thus we have shown that the indicator in terms of Tsallis-q entanglement could detect the genuine entanglement in |ψ(p)〉 better than SC.
which has two zero points at p1 = 0 and p2 ≈ 0.627. On the other hand, we can directly calculate the value of τq(|ψ(p)〉) since the Tsallis-q entanglement has an analytical formula for two-qubit quantum states. In Fig. 2 we plot the three-tangle and the indicator τq for the order q = 0.8, 1.1, 1.4. It is shown that the indicator τq is always positive for the different order q in contrast to the three-tangle τ having two zero points. Thus we have shown that the indicator in terms of Tsallis-q entanglement could detect the genuine entanglement in |ψ(p)〉 better than SC.
Monogamy relation of the μ-th power of Tsallis-q entanglement
Finally, besides the squared Tsallis-q entanglement, we can further consider the monogamy relation of the μ-th power of Tsallis-q entanglement.
For any three-qubit state  , we can obtain
, we can obtain

for all  , μ ≥ 2.
, μ ≥ 2.
For proving Eq. (12), we consider the three-qubit case, according to the monogamy relation (8), we have

for any three-qubit state  with
with  . Without loss of generality, assuming
. Without loss of generality, assuming  , we can obtain
, we can obtain

where the second inequality comes from the property (1 + x)t ≥ 1 + xt for x ≤ 1, t ≥ 1. If  or
or  , the inequality obviously holds.
, the inequality obviously holds.
Similarly, we have the following polygamy inequalities. For any three-qubit  , we have
, we have

for all  , μ ≤ 0.
, μ ≤ 0.
For any three-qubit state  with
with  , we have
, we have

where in the second inequality we have used the inequality (1 + x)t < 1 + xt for x > 0, t ≤ 0.
Discussion
In this paper we have generalized the analytic formula of Tsallis-q entanglement to the region  . Then we proved the monogamy relation in terms of STqE for an arbitrary multi-qubit systems, which include previous result in terms of EOF as a special case. Based on the monogamy properties of Tsallis-q entanglement, we have shown that the corresponding indicator can work well even when the indicator based on the squared concurrence loses its efficacy. In addition, we considered the monogamy or polygamy relation of the μ-th power of Tsallis-q entanglement. One distinct advantage of our result is that infinitely many inequalities parameterized by q provides greater flexibility than previous monogamy relation in terms of EOF.
. Then we proved the monogamy relation in terms of STqE for an arbitrary multi-qubit systems, which include previous result in terms of EOF as a special case. Based on the monogamy properties of Tsallis-q entanglement, we have shown that the corresponding indicator can work well even when the indicator based on the squared concurrence loses its efficacy. In addition, we considered the monogamy or polygamy relation of the μ-th power of Tsallis-q entanglement. One distinct advantage of our result is that infinitely many inequalities parameterized by q provides greater flexibility than previous monogamy relation in terms of EOF.
Methods
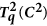 is a monotonically-increasing function of the squared concurrence C2 for all q ≥ 0
is a monotonically-increasing function of the squared concurrence C2 for all q ≥ 0
Notice that Eq. (5) can also be written as

where the function fq(x) is defined as

The squared Tsallis-q entanglement is a monotonically increasing function of C2 if the first-order derivative  with x = C2. By direct calculation, we have,
with x = C2. By direct calculation, we have,

which is always nonnegative on 0 ≤ x ≤ 1 for all q ≥ 0, where L = 1/(q − 1)2,  ,
,  , and the equality holds only at the boundary. Thus we get that
, and the equality holds only at the boundary. Thus we get that  is a monotonically increasing function of x with x = C2.
is a monotonically increasing function of x with x = C2.
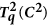 is a convex function of the squared concurrence C2 for
is a convex function of the squared concurrence C2 for 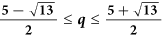
The convex property of the squared concurrence is satisfied if the second-order derivative  with x = C2. We first define a function
with x = C2. We first define a function  on the domain D = {(x, q)|0 ≤ x ≤ 1, 1 ≤ q ≤ 4}, then the nonnegativity of the second-order derivative
on the domain D = {(x, q)|0 ≤ x ≤ 1, 1 ≤ q ≤ 4}, then the nonnegativity of the second-order derivative  can be guaranteed by the nonnegativity of Fq since it varies with
can be guaranteed by the nonnegativity of Fq since it varies with  by a positive constant. After some deduction, we have
by a positive constant. After some deduction, we have

In order to prove the nonnegativity of Fq, it is suffice to consider its maximum or minimum values on the domain D. The critical points of Fq satisfy the condition

In Fig. 3(a,b), we have plotted the value of x and q which satisfies the equation ∂Fq/∂q = 0 and ∂Fq/∂x = 0 respectively. Combining the results in Fig. 3(a,b), we find that the solution of the above equation is q = 1 which is one of the boundary of domain D. To ensure the nonnegative of Fq, we should only consider the other two cases on the boundary of Fq, i.e., x = 0 and x = 1.
For the case x = 0,

which is always nonnegative in the region q ∈ (1, 4).
For the case when x = 1,

where Eq. (23) is always nonnegative for q = 1 and q = 4, and the first-order derivative of Eq. (23) increases first and then decreases for 1 ≤ q ≤ 4. Thus we prove that Eq. (23) is nonnegative in the region 1 ≤ q ≤ 4. Notice that Fq has no critical points in the interior of D, we conclude that Fq is always nonnegative for 1 ≤ q ≤ 4. The nonnegative of the Fq is also plotted in Fig. 4.
Furthermore, we can consider the nonnegative region for the second-order derivative  when q ranges in (0, 1). Under the condition
when q ranges in (0, 1). Under the condition  , we find that the critical value of x increases monotonically with the parameter q ∈ (0, 1). In Fig. 5(a), we plot the solution (x, q) to the critical condition
, we find that the critical value of x increases monotonically with the parameter q ∈ (0, 1). In Fig. 5(a), we plot the solution (x, q) to the critical condition  where for each fixed x there exists a value of q such that the second-order derivative of
where for each fixed x there exists a value of q such that the second-order derivative of  is zero. We should only consider the condition
is zero. We should only consider the condition  in the limit x → 1. In this case, we have
in the limit x → 1. In this case, we have

which gives the critical point qc3 ≈ 0.65. When q ≥ qc3, the second-order  is always positive. Similarly, we can also analyze the nonnegative region for the second-order derivative
is always positive. Similarly, we can also analyze the nonnegative region for the second-order derivative  when q ranges in (4, 5). In Fig. 5(b), it is shown that the critical value of x decreases monotonically along with the parameter q ∈ (4, 5), and the critical point qc4 ≈ 4.65. When q ≤ qc4, the second-order
when q ranges in (4, 5). In Fig. 5(b), it is shown that the critical value of x decreases monotonically along with the parameter q ∈ (4, 5), and the critical point qc4 ≈ 4.65. When q ≤ qc4, the second-order  is always positive. Notice that the analytical formula of Tq is established only for
is always positive. Notice that the analytical formula of Tq is established only for  , we conclude that the second-order derivative
, we conclude that the second-order derivative  is positive for
is positive for  which completes the proof of the convexity property of
which completes the proof of the convexity property of  with the squared concurrence C2 for
with the squared concurrence C2 for  .
.
Additional Information
How to cite this article: Yuan, G.-M. et al. Monogamy relation of multi-qubit systems for squared Tsallis-q entanglement. Sci. Rep. 6, 28719; doi: 10.1038/srep28719 (2016).
References
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Mintert, F., Kus, M. & Buchleiyner, A. Concurrence of mixed bipartite quantum states in arbitrary dimensions. Phys. Rev. Lett. 92, 167902 (2004).
Chen, K., Albeverio, S. & Fei, S. M. Concurrence of arbitrary dimensional bipartite quantum states. Phys. Rev. Lett. 95, 040504 (2005).
Breuer, H. P. Separability criteria and bounds for entanglement measures. J. Phys. A: Math. Gen. 39, 11847 (2006).
Breuer, H. P. Optimal entanglement crition for mixed quantum states. Phys. Rev. Lett. 97, 080501 (2006).
de Vicente, J. I. Lower bounds on concurrence and separability conditions. Phys. Rev. A 75, 052320 (2007).
Zhang, C. J., Zhang, Y. S., Zhang, S. & Guo, G. C. Optimal entanglement witnesses based on local orthogonal observables. Phy. Rev. A 76, 012334 (2007).
Terhal, B. M. Is entanglement monogamous? IBM J. Research and Development 48, 71 (2004).
Coffman, V., Kundu, J. & Wootters, W. K. Distributed entanglement. Phys. Rev. A 61, 052306 (2000).
Wootters, W. K. General monogamy inequality for bipartite qubit entanglement. Phys. Rev. Lett. 96, 220503 (2006).
Adesso, G. & Illuminati, F. Continuous variable tangle, monogamy inequality, and entanglement sharing in Gaussian states of continuous variable systems. New J. Phys. 8, 15 (2006).
Hiroshima, T., Adesso, G. & Illuminati, F. Monogamy inequality for distributed Gaussian entanglement. Phys. Rev. Lett. 98, 050503 (2007).
Adesso, G. & Illuminati, F. Strong monogamy of bipartite and genuine multiparitie entanglement:the Guussian case. Phys. Rev. Lett. 99, 150501 (2007).
Koashi, M. & Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 69, 022309 (2004).
Christandl, M. & Winter, A. Squashed entanglement:an additive entanglement measure. J. Math. Phys. (NY) 45, 829 (2004).
Yang, D. et al. Squashed entanglement for multipartite states and entanglement measures based on the mixed convex roof. IEEE Trans. Inf. Theory 55, 3375 (2009).
Ou, Y. C. & Fan, H. Monogamy inequality in terms of negativity for three-qubit states. Phys. Rev. A 75, 062308 (2007).
Kim, J. S., Das, A. & Sanders, B. C. Entanglement monogamy of multipartite higher-dimensional quantum systems using convex-roof extend negativity. Phys. Rev. A 79, 012329 (2009).
He, H. & Vidal, G. Disentangling theorem and monogamy for entanglement negativity. Phys. Rev. A 91, 012339 (2015).
Choi, J. H. & Kim, J. S. Negativity and strong monogamy of multiparty quantum entanglement beyond qubits. Phys. Rev. A 92, 042307 (2015).
Luo, Y. & Li, Y. Monogamy of α th power entanglement measurement in qubit system. Ann. Phys. 362, 511 (2015).
Kim, J. S. Tsallis entropy and entanglement constraints in multiqubit systems. Phys. Rev. A 81, 062328 (2010).
Kim, J. S. Generalized entanglement constraints in multi-qubit systems in terms of Tsallis entropy. arXiv:1603. 02760.
Kim, J. S. & Sanders, B. C. Monogamy of multi-qubit entanglement using Rényi entropy. J. Phys. A: Math. Theor. 43, 445305 (2010).
Cornelio, M. F. & de Oliveira, M. C. Strong superadditivity and monogamy of the Rényi measure of entanglement. Phys. Rev. A 81, 032332 (2010).
Wang, Y. X., Mu, L. Z., Vedral, V. & Fan, H. Entanglement Rényi α entropy. Phys. Rev. A 93, 022324 (2016).
Bai, Y. K., Yang, D. & Wang, Z. D. Multipartite quantum correlation and entanglement in four-qubit pure states. Phys. Rev. A 76, 022336 (2007).
Bai, Y. K. & Wang, Z. D. Multipartite entanglement in four-qubit Cluster-class states. Phys. Rev. A 77, 032313 (2008).
Ou, Y. C., Fan, H. & Fei, S. M. Proper monogamy inequality for arbitrary pure quantum states. Phys. Rev. A 78, 012311 (2008).
Jung, E., Park, D. K. & Son, J. W. Three-tangle does not properly quantify tripartite entanglement for Greenberger-Horne-Zeilinger-type states. Phys. Rev. A 80, 010301 (2009).
Eltschka, C., Osterloh, A. & Siewert, J. Possibility of generalized monogamy relations for multipartite entanglement beyond three qubits. Phys. Rev. A 80, 032313 (2009).
Ren, X. J. & Jiang, W. Entanglement monogamy inequality in a 2⊗2⊗4 system. Phys. Rev. A 81, 024305 (2010).
Cornelio, M. F. Multipartite monogamy of the concurrence. Phys. Rev. A 87, 032330 (2013).
Regula, B., DiMartino, S., Lee, S. & Adesso, G. Strong monogamy conjecture for multiqubit entanglement: the four-qubit case. Phys. Rev. Lett. 113, 110501 (2014).
Kim, J. S. Strong monogamy of quantum entanglement for multiqubit W-class states. Phys. Rev. A 90, 062306 (2014).
Bai, Y. K., Ye, M. Y. & Wang, Z. D. Entanglement monogamy and entanglement evolution in multipartite systems. Phys. Rev. A 80, 044301 (2009).
Zhu, X. N. & Fei, S. M. Entanglement monogamy relations of qubit systems. Phys. Rev. A 90, 024304 (2014).
Zhu, X. N. & Fei, S. M. Generalized monogamy relations of concurrence for N-qubit systems. Phys. Rev. A 92, 062345 (2015).
Bai, Y. K., Zhang, N., Ye, M. Y. & Wang, Z. D. Exploring multipartite quantum correlations with the square of quantum discord. Phys. Rev. A 88, 012123 (2013).
Aguilar, G. H., Valdes-Hernandez, A., Davidovich, L., Walborn, S. P. & Souto Ribeiro, P. H. Experimental entanglement redistribution under decoherence channels. Phys. Rev. Lett. 113, 240501 (2014).
Liu, F., Gao, F. & Wen, Q. Y. Linear monogamy of entanglement in three-qubit systems. Sci. Rep. 5, 16745 (2015).
Masanes, L. Universally composable privacy amplification from causality constraints. Phys. Rev. Lett. 102, 140501 (2009).
Ma, X. S., Dakic, B., Naylor, W., Zeilinger, A. & Walther, P. Quantum simulation of the wavefunction to probe frustrated Heisenberg spin systems. Nat. Phys. 7, 399 (2011).
Toner, B. Monogamy of non-local quantum correlations. Proc. R. Soc. A 465, 59 (2009).
Seevinck, M. P. Monogamy of correlations versus monogamy of entanglement. Quantum Inf. Process. 9, 273 (2010).
Garca-Saez, A. & Latorre, J. I. Renormalization group contraction of tensor networks in three dimensions. Phys. Rev. B 87, 085130 (2013).
Susskind, L. Black hole complementarity and the Harlow-Hayden conjecture. arXiv:1301. 4505.
Lloyd, S. & Preskill, J. Unitarity of black hole evaporation in final-state projection models. J High Energy Phys. 08, 126 (2014).
Bai, Y. K., Xu, Y. F. & Wang, Z. D. General monogamy relation for the entanglement of formation in multiqubit systems. Phys. Rev. Lett. 113, 100503 (2014).
Bai, Y. K., Xu, Y. F. & Wang, Z. D. Hierarchical monogamy relations for the squared entanglement of formation in multipartite systems. Phys. Rev. A 90, 062343 (2014).
Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC) under Grants No. 11374085, No. 11274010, No. 11204061; the Anhui Provincial Natural Science Foundation under Grant No. 1408085MA16; the Anhui Provincial Candidates for academic and technical leaders Foundation under Grant No. 2015H052; the discipline top-notch talents Foundation and the Excellent Young Talents Support Plan of Anhui Provincial Universities.
Author information
Authors and Affiliations
Contributions
G.-M.Y. and W.S. carried out the calculations. W.S., M.Y. and D.-C.L. conceived the idea. All authors contributed to the interpretation of the results and the writing of the manuscript. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Yuan, GM., Song, W., Yang, M. et al. Monogamy relation of multi-qubit systems for squared Tsallis-q entanglement. Sci Rep 6, 28719 (2016). https://doi.org/10.1038/srep28719
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep28719
- Springer Nature Limited
This article is cited by
-
Tighter Monogamy Relations for the Tsallis-q and Rényi-α Entanglement in Multiqubit Systems
International Journal of Theoretical Physics (2022)
-
Unified monogamy relation of entanglement measures
Quantum Information Processing (2021)
-
Tighter Monogamy and Polygamy Relations of Quantum Entanglement in Multi-qubit Systems
International Journal of Theoretical Physics (2021)
-
Tighter Monogamy Constraints in Multi-Qubit Entanglement Systems
International Journal of Theoretical Physics (2020)
-
Tighter Weighted Relations of the Tsallis-q Entanglement
International Journal of Theoretical Physics (2020)



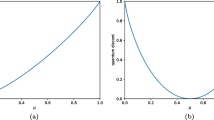

 for (a) q ∈ (0, 1) and (b) q ∈ (4, 5) respectively.
for (a) q ∈ (0, 1) and (b) q ∈ (4, 5) respectively.
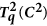 is a monotonically-increasing function of the squared concurrence C2 for all q ≥ 0
is a monotonically-increasing function of the squared concurrence C2 for all q ≥ 0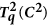 is a convex function of the squared concurrence C2 for
is a convex function of the squared concurrence C2 for 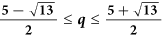

 and (b)
and (b)  respectively.
respectively.

 for (a) q ∈ (0, 1) and (b) q ∈ (4, 5) respectively.
for (a) q ∈ (0, 1) and (b) q ∈ (4, 5) respectively.