Introduction

Honeycomb lattice can host electrons with Dirac-like linear dispersion due to its C3 crystal symmetry1 and interests in questing for systems with honeycomb lattice structure flourished since the discovery of graphene produced by the scotch-tape technique2,3,4. The Dirac dispersion and the associated chiral property of electronic wave functions accommodated on honeycomb lattice make it an ideal platform for exploring topological states5,6 without external magnetic field. It was shown first that a quantum anomalous Hall effect (QAHE) can be realized when complex hopping integral among next-nearest-neighboring sites of honeycomb lattice are taken into account7. Later on it was revealed that the intrinsic spin-orbit coupling (SOC) in honeycomb lattice can provide this complex hopping integral, which drives spinful electrons into a topological state with preserved time-reversal (TR) symmetry, known as quantum spin Hall effect (QSHE)8,9,10,11. Quite a number of activities have been devoted towards realizing topological states in electron systems on honeycomb lattice, such as QAHE by straining12,13, twisting14,15 and decorating graphene16, QSHE and QAHE in terms of on-site px,y orbitals17 and QAHE with spin-polarized edge currents in terms of the antiferromagnetic exchange field and staggered electric potential18,19. Honeycomb lattice has also been explored to support topological states in photonic crystals20,21 and cold atoms with on-site p orbitals22.

In the present work, we explore possible topological properties in honeycomb lattice by introducing a texture in hopping energy between nearest-neighboring (NN) sites. We take a hexagonal primitive unit cell and view the honeycomb lattice as a triangle lattice of hexagons [see the dashed red line in Fig. 1(a)]. When the real-valued inter-hexagon hopping t1 is tuned to be larger than the intra-hexagon one t0, a topological gap is opened at the Γ point accompanied by a band inversion between orbitals with opposite spatial parities accommodated on hexagons [see Fig. 1(b)]. A pseudo-TR symmetry associated with a pseudospin degree of freedom and Kramers doubling in the emergent orbitals are revealed based on C6 point group symmetry, which generates the topology. For experimental implementations, we discuss that, along with many other possibilities, the molecular graphene realized by placing carbon monoxides (CO) periodically on Cu [111] surface13 is a promising platform to realize the present idea, where the hopping texture can be controlled by adding extra CO molecules.

Figure 1
figure 1

Hopping texture in honeycomb lattice and emergent orbitals.

(a) Honeycomb lattice with hopping energies between NN sites: t0 inside hexagons as denoted by the green bonds and t1 between hexagons by red ones. The red dashed hexagon is the primitive cell of triangular lattice with lattice vectors , and lattice constant . Numbers in circle index atomic sites within a hexagon. (b) Emergent orbitals in the hexagonal artificial atom.

Full size image

Results

Hopping texture and emergent orbitals

We start from a spinless tight-binding Hamiltonian on honeycomb lattice23

where ci is the annihilation operator of electron at atomic site i with on-site energy ε0 satisfying the anti-commutation relation, 〈i, j〉 and 〈i′, j′〉 run over NN sites inside and between hexagonal unit cells with hopping energies t0 and t1 respectively [see Fig. 1(a)]. The orbitals are considered to be the simplest one without any internal structure, such as the π electron of graphene. Below we are going to detune the hopping energy t1 while keeping t0 constant and elucidate possible changes in the electronic state. In this case, the pristine honeycomb lattice of individual atomic sites is better to be considered as a triangular lattice of hexagons, with the latter characterized by C6 symmetry.

Let us start with the Hamiltonian within a single hexagonal unit cell

where Ψ = [c1, c2, c3, c4, c5, c6]T [see Fig. 1(a)]. The eigen states of Hamiltonian H0 are given by

with eigen energies 2t0, t0, t0, −t0, −t0 and −2t0 respectively, up to normalization factors. As shown in Fig. 1(b), the emergent orbitals accommodated on the hexagonal “artificial atom” take the shapes similar to the conventional s, p, d and f atomic orbitals.

It is easy to check that the wave functions

are related each other by the operator : and with the complex conjugate operator and , where σz is the Pauli matrix. Therefore, the operator can be taken as a pseudo-TR operator and the orbital angular momentum plays the role of a pseudospin. The relation yields the Kramers doubling, a property originating from the C6 symmetry. It is noticed that the high-energy states |s〉 and are singlets and thus the pseudospin and pseudo-TR symmetry are valid only for low-energy physics, which however is sufficient for realizing nontrivial topological properties in the present system (see also ref. 21).

Distinguished from the intrinsic spin, the pseudospin is directly related to the chiral current density on the hexagon. For a lattice model, the current density between two sites is given by . The current distributions evaluated using wave functions in Eq. (4) for the pseudospin-up and -down states are shown in Fig. 2(a,b) with anticlockwisely and clockwisely circulating currents. By considering the hexagonal artificial atoms composed by six sites in honeycomb lattice, one harvests states with angular momenta merely from simple orbitals, such as π electrons in graphene. The pseudo-TR symmetry is supported by the C6 crystal symmetry, sharing the same underlying physics with the topological crystalline insulator24. However, for crystal-symmetry-protected topological insulators addressed so far, strong SOCs are required to achieve band inversions25,26,27, which is different from the present approach as revealed below.

Figure 2
figure 2

Band inversion and topological phase transition.

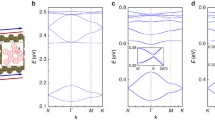
(a,b) Current densities in the pseudospin-up channel (p+ or d+) and pseudospin-down channel (p− or d−) respectively. Band dispersions for the system given in Fig. 1: (c) t1 = 0.9t0 (Inset: Brillouin zone of the triangular lattice), (d) t1 = t0 and (e) t1 = 1.1t0. Blue and red are for |p±〉 and |d±〉 orbitals respectively and rainbow for hybridization between them. The on-site energy is taken ε0 = 0.

Full size image

Topological phase transition

We calculate the energy dispersion of Eq. (1) for several typical values of t1 (hereafter the on-site energy is put as ε0 = 0 without losing generality). As shown in Fig. 2, there are two two-fold degeneracies at the Γ point corresponding to the two two-dimensional (2D) representations of C6 point group. Projecting the wave functions for t1 = 0.9t0 onto the orbitals given in Fig. 1(b), it is found that the topmost two valance bands show the character of d orbitals whereas the lowest two conduction bands behave like p orbitals [see Fig. 2(c)], with the order in energy same as those listed in Eq. (3). For t1 = t0, the d and p bands become degenerate at the Γ point and double Dirac cones appear [see Fig. 2(d)], which are equivalent to the ones at K and K′ points in the unfolded Brillouin zone of honeycomb lattice with the rhombic unit cell of two sites. When t1 increases further from t0, a band gap reopens at the Γ point. As shown in Fig. 2(e) for t1 = 1.1t0, the valence (conduction) bands are now occupied by p (d) orbitals around the Γ point, opposite to the order away from the Γ point and to that before gap closing. Therefore, a band inversion between p and d orbitals takes place at the Γ point when the inter-hexagon hopping energy is increased across the topological transition point t1 = t0, namely the pristine honeycomb lattice.

We can characterize the topological property of the gap-opening transition shown in Fig. 2 by a low-energy effective Hamiltonian around the Γ point. Since the bands near the Fermi level are predominated by p and d orbitals, it is sufficient to downfold the six-dimensional Hamiltonian H(k) associated with the tight-binding model (1) into the four-dimensional subspace [p+, d+, p−, d−]. The second term in Eq. (1) is then simply given by

Contributions from the third term in Eq. (1) to the effective Hamiltonian can be evaluated in the following way28. First, we list the inter-hexagon hoppings in terms of 6 × 6 matrices and with

on the basis of [c1, c2, c3, c4, c5, c6]. Following the standard procedures28, they can be projected to the subspace spanned by [p+, d+, p−, d−]

With Fourier transformations of matrices in Eqs. (5) and (6), one obtains the effective low-energy Hamiltonian H′(k) on the basis [p+, d+, p−, d−] in the momentum space. Expanding H′(k) around the Γ point up to the lowest-orders of k, one arrives at

with

where , k = (kx, ky), k± = kx ± iky, 0 is a 2 × 2 zero matrix and a0 is the lattice constant of the triangular lattice. For δt = 0, the Hamiltonians H+(k) and H−(k) in Eq. (8) are the same as the well-known one for honeycomb lattice around the K and K′ points29, where the quadratic terms of momentum in the diagonal parts can be neglected.

For δt > 0, however, the quadratic terms are crucially important since they induce a band inversion30, resulting in the orbital hybridization in the band structures shown in Fig. 2(e). Associated with a skyrmion in the momentum space for the orbital distributions in the individual pseudospin channels, a topological state appears characterized by the topological invariant10,11,21,31. It is clear that for δt < 0 there is no band inversion taking place and thus the band gap is trivial as shown in Fig. 2(c).

The pseudo-TR symmetry satisfying is preserved at the Γ point. Going away from the Γ point, the C6 symmetry is gradually broken, so does the pseudo-TR symmetry and the two pseudospin channels start to mix with each other. However, this mixing is weak around the Γ point where the topological property of the system is determined. This can be seen directly from the band structure shown in Fig. 2(e) [as well as in Fig. 2(c,d)], where a gap between p+ and p− (d+ and d−) is hardly observed around the Γ point. Analytically, the matrix elements between the two pseudospin channels in the Hamiltonian (7) are quadratic in momentum, which can be neglected as high-order corrections when the topological property is addressed.

It is worthy noticing that, comparing with the Kane-Mele model for the honeycomb lattice10,11, the mass term δt(>0) in Eq. (8) can be considered as an effective SOC associated with the pseudospin, namely λeSOC = δt. For δt = 0.1t0, a moderate texture in hopping energies, the effective SOC is approximately 3000 times larger than the real SOC in magnitude in graphene where λSOC ≃ 0.1 meV and t0 = 2.7 eV. The huge effective SOC is due to its pure electronic character as compared with the intrinsic SOC originated from the relativistic effect. This is one of the fantastic aspects of the present approach, which renders a topological gap corresponding to temperature of thousands of Kelvin.

Topological edge states and associated conductances

We consider a ribbon of hexagonal unit cells of t1 = 1.1t0 with its two edges cladded by hexagonal unit cells of t1 = 0.9t0. As can be seen in Fig. 3(a), additional states appear in the bulk gap as indicated by the red solid curves carrying double degeneracy. Plotting the spatial distribution of the corresponding wave functions, we find that the in-gap states are localized at the two interfaces between topological and trivial regions [see Fig. 3(b)]. As displayed in Fig. 3(c,d), there is an excess upward (downward) edge current in the pseudospin-up (-down) channel associated with the state indicated by the red (green) dot in Fig. 3(a).

Figure 3
figure 3

Topological edge states.

(a) Band dispersion of a ribbon system of 36 hexagons with t1 = 1.1t0 cladded from both sides by 10 hexagons with t1 = 0.9t0. (b) Real-space distribution of the in-gap states associated with the red solid dispersion curves in (a). (c,d) Real-space distributions of current densities in pseudospin-up and -down channels at the momenta indicated by the red and green dots 1 and 2 in (a) within the rhombic area sketched by dashed line in (b); the excess currents in pseudospin-up and -down channels are indicated by red and green arrows in (b).

Full size image

At the interface between topological and trivial regimes, the crystal symmetry is reduced from C6 to C2, which breaks the pseudo-TR symmetry in contrast to the real TR symmetry. As the result, a mini gap of ~0.01t0 [unnoticeable in the scale of Fig. 3(a)] opens in the edge states at the Γ point due to the coupling between two pseudospin channels. In order to quantitatively check possible backscatterings caused by this mini gap, we perform calculations on the longitudinal and Hall conductances based on a Hall bar system as sketched in Fig. 4(a). It is clear that the current I injected from the left electrode divides itself into two branches according to the pseudospin states, namely pseudospin-up (-down) electrons can flow only in the upper (lower) edge of the Hall bar. By matching wave functions at the interfaces between the six semi-infinite electrodes and the topological scattering region32,33, one can evaluate the transmissions of plane waves scattered among all the six leads and then the longitudinal and Hall conductances, and respectively, by the Landauer-Büttiker formalism34, where ρxx and ρxy are the longitudinal and transverse resistances, respectively. Similar to the case of QSHE with magnetic impurities35, the values of conductivity in the present system deviate from the quantized ones when the Fermi level falls in the mini gap of ~0.01t0 as shown in Fig. 4(b). It is noticed, however, that both Gxx and Gxy heal quickly after several periods of oscillations that come from interferences between the two pseudospin channels. It is emphasized that almost perfectly quantized conductances Gxx = 2e2/h and Gxy = 030,36 are achieved for the Fermi level beyond 0.04t0 up to the bulk gap edge at 0.1t0, where the edge states with almost perfect linear dispersions hardly feel the existence of the mini gap and essentially no appreciable backscattering exists. On the other hand, if the inter-hexagon hopping energy is put far away from the intra-hexagon one in topological and/or trivial regimes, edge states may hardly be noticed37.

Figure 4
figure 4

Conductances of the topological phase.

(a) Schematic configuration of a six-terminal Hall bar where a topological sample (light blue region) with t1 = 1.1t0 is embedded in a trivial environment (gray region) with t1 = 0.9t0. The size of topological scattering region is 240a0 × 120a0 and the width of each semi-infinite lead is 40a0. The injected current flows along the edges of topological sample as indicated by the red parts between electrodes. (b) Longitudinal and Hall conductances of the Hall bar as a function of energy of incident electrons. The on-site energy is taken ε0 = 0. A rhombic topological sample is taken for ease of calculation.

Full size image

Now we investigate the hopping-energy dependence of the longitudinal conductance. The size of scattering region is same as in Fig. 4(a) and fixed for all cases. As displayed in Fig. 5(a), Gxx saturates to the quantized value 2e2/h as expected for a topological state for all the cases with t1 = 1.05t0, 1.1t0 and 1.2t0 in the topological region (whereas 0.95t0, 0.9t0 and 0.8t0 in the trivial region correspondingly) when the Fermi level is set away from the mini gaps, accompanied by oscillations due to interferences between the two pseudospin channels.

Figure 5
figure 5

Hopping-energy and sample-size dependence of longitudinal conductances.

Longitudinal conductance Gxx of the topological sample given in Fig. 4(a) as a function of the energy of injected electrons: (a) for several typical values of inter-hexagon hopping integrals [1.05t0, 0.95t0], [1.1t0, 0.9t0] and [1.2t0, 0.8t0], where the first (second) inside bracket is for the topological (trivial) region; (b) with several typical system sizes , where the width of the electrodes is fixed at 40a0 and the inter-hexagon hopping integral is fixed at t1 = 1.1t0 and t1 = 0.9t0 for the topological and trivial regions respectively.

Full size image

We then check the sample-size dependence of the longitudinal conductance. We fix inter-hexagon hopping integrals at 1.1t0 and 0.9t0 in the topological and trivial regions respectively. As displayed in Fig. 5(b), Gxx saturates in all cases to the quantized value 2e2/h when the Fermi level is shifted away from the mini gap. The topological edge transports remain unchanged when the size of the topological region becomes large.

Real spin and QSHE

In addition to the pseudospin, the real spin degree of freedom also contributes to transport properties. In absence of the real SOC, the results presented in Fig. 4 remain exactly the same, with an additional double degeneracy due to the two spin channels and thus Gxx = 4e2/h.

An intrinsic SOC is induced when next-nearest-neighbor hoppings in honeycomb lattice are taken into account10,11. The low-energy Hamiltonian around the Γ point in Eq. (7) is then modified to

with

where ν = 1 and −1 stand for spin-up and -down states respectively. Therefore, in the spin-up channel SOC enhances (suppresses) the topological gap in the pseudospin-up (-down) channel presuming λ > 0 [see the left and central panels of Fig. 6(a)]. As far as λ < δt, the system remains the topological state associated with the pseudospin, where electrons with up pseudospin and down pseudospin counter propagate at edges, both carrying on up and down spins. The longitudinal conductance Gxx saturates to 4e2/h as displayed in Fig. 6(b).

Figure 6
figure 6

Edge states and conductances of the topological phase in the presence of SOC.

(a) Dispersion relations and (b) longitudinal conductances of the topological system same as that given in Fig. 4(a) except that finite SOC is included.

Full size image

When SOC is increased to λ = δt, the pseudospin-down (-up) channel with up (down) spin is driven into a semi-metallic state with zero band gap and the Dirac dispersion appears at the Γ point. When SOC goes beyond δt, this Dirac dispersion opens a gap accompanied by a topological phase transition. The system now takes a QSHE state where at edges electrons with up spin and pseudospin propagate oppositely to electrons with down spin and pseudospin. Evaluating the longitudinal conductance, one finds that Gxx is quantized exactly to 2e2/h [see Fig. 6(b)] and as shown in the right panel of Fig. 6(a) there is no mini gap in the edge states, as protected by real TR symmetry10,11.

Discussions

A tight-binding model for spinless fermions on honeycomb lattice was considered in a previous work with a Kekulé pattern in nearest-neighbor hopping integrals23. It was revealed that fractional charges can be achieved when the mass gap contains a vortex, which requires the hopping integral depending on position in a special way. In contrast, in the present model Hamiltonian (1) there are only two values of hopping integral and when the inter-hexagon one is larger than the intra-hexagon one a topological state characterized by emergent pseudospin degree of freedom appears.

We then discuss possible experimental realization of our theoretical proposal. Much effort has been devoted towards realizing the Dirac-like energy dispersion in artificial honeycomb lattices38, ranging from optical lattices39,40 to 2D electron gases modulated by periodic potentials13,41,42 and In2Te2/graphene bilayers43. All these systems provide promising platforms for realizing topological properties by detuning effective hopping energy among NN sites either by modulating muffin-tin potentials or bond lengthes periodically. To be specific, here we focus on how to achieve a topological state on the Cu [111] surface modulated by triangular gates of carbon monoxide (CO) molecules13. When extra CO molecules are placed at specific positions over the pristine molecular graphene, the bonds of the hexagons surrounding them are elongated since the CO clusters enhance local repulsive potentials and push electrons away from them, which reduces the corresponding electron hopping energies42. It is extremely interesting from the present point of view that hopping textures with C6 symmetry have already been achieved in experiments13. We propose to place extra CO atoms in the pattern displayed in Fig. 7(a), where the intra-hexagon hopping energy t0 (green thin bonds) surrounding the CO clusters is reduced and the inter-hexagon hopping energy t1 (red thick bonds) is enhanced relatively. According to the above discussions, the system displayed in Fig. 7(a) with t1 > t0 should take a topological state. The hopping texture in Fig. 7(b), dual to that shown in Fig. 7(a), was realized in experiments13, where the system takes a topologically trivial state because t1 < t0 (see also ref. 44).

Figure 7
figure 7

Schematics for hopping textures with C6 symmetry.

Molecular graphene realized by decorating the Cu [111] surface with a triangular lattice of CO molecules: (a) t1 > t0 generating topological state, (b) t1 < t0 for trivial state. Gray balls are CO molecules decorated by STM techniques and red thick bonds are shorter than green thin ones which generates the hopping textures.

Full size image

The underlying idea of the present scheme for achieving the topological state is to create artificial orbitals carrying on opposite orbital angular momenta and parities with respect to spatial-inversion symmetry and to induce a band inversion between them by introducing the hopping texture with C6 symmetry on honeycomb lattice. In the sense that it does not require SOC, the present state may be understood as a quantum orbital Hall effect. The topological properties can also be extended to photonic crystals21, cold atoms, physical systems of exciton, polariton, surface plasmon and phonon.

In conclusion, we propose to derive topological properties by modulating electron hopping energy between nearest-neighbor sites of honeycomb lattice. Because of the hopping texture with C6 symmetry, atomic-like orbitals emerge, which carry a pseudospin degree of freedom characterizing a pseudo time-reversal symmetry and rendering Kramers pairs. We reveal that the effective spin-orbit coupling associated with the pseudospin degree of freedom can be larger than the intrinsic one by orders of magnitude because of the pure electronic origin. The present work offers a new possibility for achieving topological properties and related novel quantum properties and functionalities at high temperatures.

Methods

Energy dispersion relations are obtained by direct diagonalizations of Hamiltonian. Calculations of longitudinal and Hall conductances are performed by using open software Kwant33.

Additional Information

How to cite this article: Wu, L.-H. and Hu, X. Topological Properties of Electrons in Honeycomb Lattice with Detuned Hopping Energy. Sci. Rep. 6, 24347; doi: 10.1038/srep24347 (2016).