Abstract
Quantum repeater is one of the important building blocks for long distance quantum communication network. The previous quantum repeaters based on atomic ensembles and linear optical elements can only be performed with a maximal success probability of 1/2 during the entanglement creation and entanglement swapping procedures. Meanwhile, the polarization noise during the entanglement distribution process is harmful to the entangled channel created. Here we introduce a general interface between a polarized photon and an atomic ensemble trapped in a single-sided optical cavity and with which we propose a high-efficiency quantum repeater protocol in which the robust entanglement distribution is accomplished by the stable spatial-temporal entanglement and it can in principle create the deterministic entanglement between neighboring atomic ensembles in a heralded way as a result of cavity quantum electrodynamics. Meanwhile, the simplified parity-check gate makes the entanglement swapping be completed with unity efficiency, other than 1/2 with linear optics. We detail the performance of our protocol with current experimental parameters and show its robustness to the imperfections, i.e., detuning and coupling variation, involved in the reflection process. These good features make it a useful building block in long distance quantum communication.
Similar content being viewed by others
Introduction
Quantum mechanics provides some interesting ways for communicating information securely between remote parties1,2,3,4,5. However, in practice the quantum channels such as optical fibers are noisy and lossy6. The transmission loss and the decoherence of photon systems increase exponentially with the distance, which makes it extremely hard to perform a long-distance quantum communication directly. To overcome this limitation, Briegel et al.7 proposed a noise-tolerant quantum repeater protocol in 1998. The channel between the two remote parties A and B is divided into smaller segments by several nodes, the neighboring nodes can be entangled efficiently by the indirect interaction through flying qubits and the entanglement between non-neighboring nodes is implemented by quantum entanglement swapping, which can be cascaded to create the entanglement between the terminate nodes A and B.
The implementation of quantum repeaters is compatible with different physical setups assisted by cavity quantum electrodynamics, such as nitrogen vacancy centers in diamonds8, spins in quantum dots9,10,11,12, single trapped ions or atoms13,14. However, the most widely known approach for quantum repeaters is based on atomic ensembles15 due to the collective enhancement effect16. In a seminal paper by Duan et al.17, the atomic ensemble is utilized to act as a local memory node. The heralded collective spin-wave entanglement between the neighboring nodes is established by the detection of a single Stokes photon, emitted indistinguishably from either of the two memory nodes via a Raman scattering process. However, due to the low probability of Stokes photon emission required in the Duan-Lukin-Cirac-Zoller (DLCZ) proposal17, the parties can hardly establish the entanglement efficiently for quantum entanglement swapping. In order to improve the success probability, photon-pair sources and multimode memories are used to construct a temporal multi-mode modification18 and then the schemes based on the single-photon sources19 and spatial multiple modes20 are developed. Besides these protocols based on Mach-Zehnder-type interference, Zhao et al.21,22 proposed a robust quantum repeater protocol based on two-photon Hong-Ou-Mandel-type interference, which relaxes the long-distance stability requirements and suppresses the vacuum component to a constant item. Subsequently, the single-photon sources are embedded to improve the performance of robust quantum repeaters23,24,25. In addition, Rydberg blockade effect26 is used to perform controlled-NOT gate between the two atomic ensembles in the middle node27,28, which makes the quantum entanglement swapping operation be performed deterministically.
Since the two-photon interference is performed with the polarization degree of freedom (DOF) of the photons21,22, which is incident to be influenced by the thermal fluctuation, vibration and the imperfection of the fiber29, the fidelity of the entanglement created between the neighboring nodes will be decreased when the photons are transmitted directly6,7. In other words, the more the overlap of the initial photon state used in the two-photon interference is, the higher the fidelity of the entanglement created is. Following the idea of Zhao’s protocol21, quantum repeaters immune to the rotational polarization noise are proposed with the time-bin photonic state30 and the antisymmetric Bell state31  , respectively. When the noise on the two orthogonal polarized photon states is independent, Zhang et al.32 utilized the faithful transmission of polarization photons29 to surmount the collective noise. In the ideal case, the two-fold coincidence detection in the central node can successfully get the stationary qubits entangled maximally in a heralded way. Apart from this type of entanglement distribution, Kalamidas33 proposed an error-free entanglement distribution protocol in the linear optical repeater. An entangled photon source is placed at the center node and the entangled photons transmitted to neighboring nodes are encoded with their time-bin DOF. With two fast Pockels cells (PCs), the entanglement distribution can be performed with a high efficiency when the polarization-flip-error noise is relatively small.
, respectively. When the noise on the two orthogonal polarized photon states is independent, Zhang et al.32 utilized the faithful transmission of polarization photons29 to surmount the collective noise. In the ideal case, the two-fold coincidence detection in the central node can successfully get the stationary qubits entangled maximally in a heralded way. Apart from this type of entanglement distribution, Kalamidas33 proposed an error-free entanglement distribution protocol in the linear optical repeater. An entangled photon source is placed at the center node and the entangled photons transmitted to neighboring nodes are encoded with their time-bin DOF. With two fast Pockels cells (PCs), the entanglement distribution can be performed with a high efficiency when the polarization-flip-error noise is relatively small.
In a recent work, Mei et al.34 built a controlled-phase-flip (CPF) gate between a flying photon and an atomic ensemble embedded in an optical cavity and constructed a quantum repeater protocol, following some ideas in the original DLCZ scheme17. In 2012, Brion et al.35 constituted a quantum repeater protocol with Rydberg blocked atomic ensembles in fiber-coupled cavities via collective laser manipulations of the ensembles and photon transmission. Besides, Wang et al.36 proposed a one-step hyperentanglement distillation and amplification proposal and Zhou and Sheng37 designed a recyclable protocol for the single-photon entanglement amplification, which are quite useful to the high dimensional or multiple DOFs optical quantum repeater.
In this paper, we give a general interface between a polarized photon and an atomic ensemble trapped in a single-sided optical cavity. Besides, we show that a deterministic faithful entanglement distribution in a quantum repeater can be implemented with the time-bin photonic state when two identical fibers act as the channels of different spatial DOFs of the photons. Interestingly, it does not require fast PCs and the time-slot discriminator29,30,31,32,33 is not needed anymore. By using the input-output process of a single photon based on our general interface, the entanglement between the neighboring atom ensembles can be created in a heralded way, without any classical communication after the clicks of the photon detectors and the quantum swapping can be implemented with almost unitary success probability by a simplified parity-check gate (PCG) between two ensembles, other than 1/2 with linear optics. We analyze the performance of our high-efficiency quantum repeater protocol with current experimental parameters and show its robustness to the imperfections involved in the reflection process. These good features will make it a useful building block in long-distance quantum communication in future.
Results
A general interface between a polarized photon and an atomic ensemble
The elementary node in our quantum repeater protocol includes an ensemble with N cold atoms trapped in a single-sided optical cavity34,35. The atom has a four-level internal structure and its relevant levels are shown in Fig. 1. The two hyperfine ground states are denoted as  and
and  . The excited state
. The excited state  and the Rydberg state
and the Rydberg state  are two auxiliary states. The
are two auxiliary states. The  polarized cavity mode ah couples to the transition between
polarized cavity mode ah couples to the transition between  and
and  . Initially, all of the atoms are pumped to the state
. Initially, all of the atoms are pumped to the state  . With the help of the Rydberg state
. With the help of the Rydberg state  , one can efficiently perform an arbitrary operation between the ground state
, one can efficiently perform an arbitrary operation between the ground state  and the single collective spin-wave excitation state17
and the single collective spin-wave excitation state17  via collective laser manipulations of the ensembles34,35,38. The single collective excited state
via collective laser manipulations of the ensembles34,35,38. The single collective excited state  . When the Rydberg blockade shift is of the scale 2π × 100 MHz, the transition between
. When the Rydberg blockade shift is of the scale 2π × 100 MHz, the transition between  and
and  can be completed with an effective coupling strength 2π × 1 MHz and the probability of nonexcited and doubly excited errors39 is about 10−3–10−4. Recently, rotations along axes Rx, Ry and Rz of a spin-wave excitation with an average fidelity of 99% are achieved in 87Rb atomic ensembles and they are implemented by making use of stimulated Raman transition and controlled Larmor procession40. In other words, the high-efficiency single qubit rotations of the atomic ensemble can be implemented faithfully.
can be completed with an effective coupling strength 2π × 1 MHz and the probability of nonexcited and doubly excited errors39 is about 10−3–10−4. Recently, rotations along axes Rx, Ry and Rz of a spin-wave excitation with an average fidelity of 99% are achieved in 87Rb atomic ensembles and they are implemented by making use of stimulated Raman transition and controlled Larmor procession40. In other words, the high-efficiency single qubit rotations of the atomic ensemble can be implemented faithfully.
Let us consider an  polarized input photon with the frequency ω, which is nearly resonant to the cavity mode
polarized input photon with the frequency ω, which is nearly resonant to the cavity mode  with the frequency ωc. The coupling rate between the cavity and the input photon can be taken to be a real constant
with the frequency ωc. The coupling rate between the cavity and the input photon can be taken to be a real constant  when the detuning |δ′| = |ω − ωc| is far less than the cavity decay rate κ (|δ′| ≪ κ)41,42,43. The Hamiltonian of the whole system, in the frame rotating with respect to the cavity frequency ωc, is (ħ = 1)41
when the detuning |δ′| = |ω − ωc| is far less than the cavity decay rate κ (|δ′| ≪ κ)41,42,43. The Hamiltonian of the whole system, in the frame rotating with respect to the cavity frequency ωc, is (ħ = 1)41

where  and
and  are the operators of the cavity mode and the input photon with the properties
are the operators of the cavity mode and the input photon with the properties  and
and  , respectively. Δ = ω0 − ωc is the detuning between the cavity mode frequency ωc and the dipole transition frequency ω0,
, respectively. Δ = ω0 − ωc is the detuning between the cavity mode frequency ωc and the dipole transition frequency ω0,  and
and  .
.  represents the spontaneous emission rate of the excited state
represents the spontaneous emission rate of the excited state  , while gj denotes the coupling strength between the j-th atom transition and the cavity mode
, while gj denotes the coupling strength between the j-th atom transition and the cavity mode  . Here and after, we assume gj = g and
. Here and after, we assume gj = g and  for simplicity.
for simplicity.
With the Hamiltonian  shown in Eq. (1), the Heisenberg-Langevin equations of motion for cavity
shown in Eq. (1), the Heisenberg-Langevin equations of motion for cavity  and the atomic operator
and the atomic operator  taking into account the atomic excited state decay γ can be detailed as41
taking into account the atomic excited state decay γ can be detailed as41

Here the Pauli operator  , while
, while  is corresponding to the vacuum noise field that helps to preserve the desired commutation relations for the atomic operator. Along with the standard cavity input-output relation
is corresponding to the vacuum noise field that helps to preserve the desired commutation relations for the atomic operator. Along with the standard cavity input-output relation  , one can obtain the reflection and noise coefficients r(δ′) and n(δ′) in the weak excitation approximation where the ensemble is hardly in the state
, one can obtain the reflection and noise coefficients r(δ′) and n(δ′) in the weak excitation approximation where the ensemble is hardly in the state  but predominantly in
but predominantly in  , that is,
, that is,

where Δ′ = ω − ω0 represents the frequency detuning between the input photon and the dipole transition. |r(δ′)|2 + |n(δ′)|2 = 1 means that when the noise field is considered, the energy is conserved during the input-output process of the single-sided cavity.
If the atomic ensemble in the cavity is initialized to be the state  , it does not interact with the cavity mode (i.e., g = 0). The input
, it does not interact with the cavity mode (i.e., g = 0). The input  polarized probe photon feels an empty cavity and will be reflected by the cavity directly. Now, the reflection coefficient can be simplified to be41
polarized probe photon feels an empty cavity and will be reflected by the cavity directly. Now, the reflection coefficient can be simplified to be41

Note that the detuning is small  , the pulse bandwidth is much less than the cavity decay rate κ. If the strong coupling condition
, the pulse bandwidth is much less than the cavity decay rate κ. If the strong coupling condition  is achieved, one can get the input probe photon totally reflected with
is achieved, one can get the input probe photon totally reflected with  or
or  , shown in Fig. 2. The absolute phase shifts versus the scaled detuning are shown in Fig. 3.
, shown in Fig. 2. The absolute phase shifts versus the scaled detuning are shown in Fig. 3.
(a) |r| |n| and |r0| vs the scaled detuning δ′/κ, with the scaled coupling rate53 g/κ = 4.0566 and γ/κ = 0.0566. (b) |r| vs the scaled coupling rate g/κ with detuning δ′/γ = 0, 0.5 and 1.
The absolute phase shifts vs the scaled detuning.
The dashed and dashed-dot lines show the absolute phase shifts |θ0/π| and |θ/π| that the reflected photon gets, with the ensemble in the states  and
and  , respectively. The solid line represents the absolute value of the phase shifts difference |Δθ/π| = |θ0/π − θ/π|. The inset shows the phase shifts vs the scaled detuning. θ0/π and θ/π that the reflected photon gets, with the ensemble in
, respectively. The solid line represents the absolute value of the phase shifts difference |Δθ/π| = |θ0/π − θ/π|. The inset shows the phase shifts vs the scaled detuning. θ0/π and θ/π that the reflected photon gets, with the ensemble in  and
and  , respectively.
, respectively.
Hybrid CPF gate on a photon-atomic-ensemble system and PCG on a two-atomic-ensemble system
The principle of our CPF gate on a hybrid quantum system composed of a photon p and an atomic ensemble EA is shown in Fig. 4, following some ideas in previous works34,42,43. Suppose that the photon p is in the state  (|μ|2 + |ν|2 = 1) and the ensemble EA is in the state
(|μ|2 + |ν|2 = 1) and the ensemble EA is in the state  (|μ′|2 + |ν′|2 = 1). The
(|μ′|2 + |ν′|2 = 1). The  polarized component of the photon p transmits the polarization beam splitter (PBS) and then be reflected by the cavity, while the
polarized component of the photon p transmits the polarization beam splitter (PBS) and then be reflected by the cavity, while the  polarized component is reflected by the mirror M. The optical pathes of the
polarized component is reflected by the mirror M. The optical pathes of the  and
and  components are adjusted to be equal and they will be combined again at the PBS with an extra π phase shift on the
components are adjusted to be equal and they will be combined again at the PBS with an extra π phase shift on the  component if the ensemble is in the state
component if the ensemble is in the state  . This process can be described as
. This process can be described as

That is to say, the setup in Fig. 4(a) can be used to accomplish a CPF gate on the atomic ensemble EA and the photon p.
The schematic diagram of our PCG on two atomic ensembles EA and  is shown in Fig. 4(b). Let us assume that EA and EB are initially in the states
is shown in Fig. 4(b). Let us assume that EA and EB are initially in the states  (|μi|2 + |νi|2 = 1 and i = A, B). One can input a polarized photon p in the state
(|μi|2 + |νi|2 = 1 and i = A, B). One can input a polarized photon p in the state  into the import of the setup. HWP1 (HWP2) is used to perform the bit-flip operation
into the import of the setup. HWP1 (HWP2) is used to perform the bit-flip operation  on the photon p by using a half-wave plate (HWP) with its axis at π/4 with respect to the horizontal direction. After the two components of p are reflected by the two cavities, they combine with each other at PBS2. The state of the system composed of the two atom ensembles and the photon evolves to be
on the photon p by using a half-wave plate (HWP) with its axis at π/4 with respect to the horizontal direction. After the two components of p are reflected by the two cavities, they combine with each other at PBS2. The state of the system composed of the two atom ensembles and the photon evolves to be

And then, another HWP names H whose axis is placed at π/8 is used to perform a Hadamard rotations  and
and  on the photon. The state of the system becomes
on the photon. The state of the system becomes

After the photon is measured with PBS3 and two single-photon detectors, the parity of EA and EB can be determined. In detail, if the photon is in the state  , the two ensembles EA and EB have an even parity. If the photon is in
, the two ensembles EA and EB have an even parity. If the photon is in  , EA and EB have an odd parity. With an effective input-output process of a single photon, one can efficiently complete the PCG on two atomic ensembles.
, EA and EB have an odd parity. With an effective input-output process of a single photon, one can efficiently complete the PCG on two atomic ensembles.
Entanglement distribution with faithful single-photon transmission
Suppose that there is an entanglement source which is placed at a central station between two neighboring nodes, say Alice and Bob. The source produces a two-photon polarization-entangled Bell state  . Here the subscripts a and b denote the photons sent to Alice and Bob, respectively. As shown in Fig. 5(a), the photons a and b will pass through an encoder in each side before they enter the noisy channels. The encoder is made up of a PBS, an HWP and a beam splitter (BS). Here BS is used for a Hadamard rotation on the spatial DOF of the photon, i.e.,
. Here the subscripts a and b denote the photons sent to Alice and Bob, respectively. As shown in Fig. 5(a), the photons a and b will pass through an encoder in each side before they enter the noisy channels. The encoder is made up of a PBS, an HWP and a beam splitter (BS). Here BS is used for a Hadamard rotation on the spatial DOF of the photon, i.e.,  and
and  , where
, where  and
and  represent the upper and the down ports of the BS, respectively.
represent the upper and the down ports of the BS, respectively.
With our faithful single-photon transmission method (see Method), Alice and Bob can share photon pairs in a maximally entangled state, shown in Fig. 5. In detail, after a photon pair from the source passes through the two encoders, its state becomes

As the two photons a and b suffer from independent collective noises from the two channels, the influence of the channels on the two photons can be described with two unitary rotations  and
and  as follows:
as follows:


where |δi|2 + |ηi|2 = 1 (i = a, b). The influence on the polarization of the photons arising from the channel noises can be totally converted into that on the spatial DOF. The state of the photons a and b arriving at Alice and Bob becomes

This is a two-photon Bell state  in the polarization DOF of the photon pair ab. Simultaneously, it is a separable superposition state
in the polarization DOF of the photon pair ab. Simultaneously, it is a separable superposition state  in the spatial DOF.
in the spatial DOF.
To entangle the stationary atomic ensembles EA and EB, which are initialized to be  and
and  , only two CPF gates are required if Alice and Bob have shared some photon pairs in the Bell state
, only two CPF gates are required if Alice and Bob have shared some photon pairs in the Bell state  . Let us take the case that the photons a and b come from the spatial modes a2 and b2 as an example to detail the entanglement creation process. As for the other cases, the same entanglement between EA and EB can be obtained by a similar procedure with or without some single-qubit operations.
. Let us take the case that the photons a and b come from the spatial modes a2 and b2 as an example to detail the entanglement creation process. As for the other cases, the same entanglement between EA and EB can be obtained by a similar procedure with or without some single-qubit operations.
First, the photon a suffers a Hadamard operation by passing through a half-wave plate H. Second, it is reflected by the cavity or the mirror M, which is used to complete the CPF gate on the photon a and the ensemble EA. Third, Alice performs another Hadamard operation on the photon a. Now, the state of the composite system composed of the photons a and b and the ensembles EA and EB evolves into  ,
,

Fourth, Alice measures the polarization state of the photon a with a setup composed of PBS and single-photon detectors Dh and Dv. If an  polarized photon is detected, the hybrid system composed of b, EA and EB will be projected into
polarized photon is detected, the hybrid system composed of b, EA and EB will be projected into

If a  polarized photon is detected, the remaining hybrid system can also be transformed into the state
polarized photon is detected, the remaining hybrid system can also be transformed into the state  by a bit-flip operation
by a bit-flip operation  on the ensemble EA.
on the ensemble EA.
Up to now, the original entanglement of the photon pair ab is mapped to the hybrid entanglement between the photon b and the ensemble EA. In order to create the entanglement between EA and EB, Bob just performs the same operations as Alice does. In brief, before and after the CPF operation on the photon b and the ensemble EB, Bob performs two local Hadamard operations on the photon b with H. These operations result in the entanglement between the photon b and the two atomic ensembles. The state  is changed into
is changed into 

If the detector Dh at Bob’s node is clicked, the state of the system composed of EA and EB will be collapsed into the desired entangled state

As for the case that the photon b is in the state  , they can also obtain the desired entangled state
, they can also obtain the desired entangled state  with an additional bit-flip operation
with an additional bit-flip operation  on EB.
on EB.
Entanglement swapping on atomic ensembles with a PCG
After the parties produce successfully the entanglement between each two atomic ensembles in the neighboring nodes, they can extend the entanglement to a further distance by entanglement swapping. Let us use the case with three nodes as an example to describe the principle for connecting the two non-neighboring nodes.
Suppose the atomic ensembles EA and EC belong to the two non-neighboring nodes Alice and Charlie, respectively and the two ensembles  and
and  belong to the middle node Bob, shown in Fig. 6. The two ensembles
belong to the middle node Bob, shown in Fig. 6. The two ensembles  are in the state
are in the state  and the two ensembles
and the two ensembles  are in the state
are in the state  . After a parity-check measurement performed on the two local ensembles
. After a parity-check measurement performed on the two local ensembles  and
and  with a PCG shown in Fig. 3(b), the state of the system composed of the four ensembles EA, EC,
with a PCG shown in Fig. 3(b), the state of the system composed of the four ensembles EA, EC,  and
and  evolves into an entangled one. If the outcome of the parity-check measurement on the ensembles B1B2 is odd, the composite system composed of
evolves into an entangled one. If the outcome of the parity-check measurement on the ensembles B1B2 is odd, the composite system composed of  ,
,  , EA and
, EA and  will be projected into the state
will be projected into the state

which is a four-qubit Greenberger-Horne-Zeilinger state. The decoherence of both  and
and  has an awful influence on the system composed of EA and EC as it decreases the fidelity of the entanglement of the system. In order to disentangle the two ensembles
has an awful influence on the system composed of EA and EC as it decreases the fidelity of the entanglement of the system. In order to disentangle the two ensembles  and
and  from the system, the party at the middle node could first perform a Hadamard operation on the two ensembles and then apply a parity-check measurement on them. If the outcome of the second parity-check measurement is even, the composite system composed of the four ensembles
from the system, the party at the middle node could first perform a Hadamard operation on the two ensembles and then apply a parity-check measurement on them. If the outcome of the second parity-check measurement is even, the composite system composed of the four ensembles  ,
,  , EA and EC is projected into the state
, EA and EC is projected into the state

where the ensembles  and
and  are decoupled from the system composed of the two nonlocal ensembles EA and EC which are in the maximally entangled state
are decoupled from the system composed of the two nonlocal ensembles EA and EC which are in the maximally entangled state  .
.
In the discussion above, we use the outcomes (odd, even) of the two successive parity-check measurements as an example to describe the principle of the entanglement swapping between the four atomic ensembles. In fact, the other cases that the outcomes of each parity-check measurement is either an odd one or an even one can also be used for the entanglement swapping with only a single-qubit operation on the ensemble EA, shown in Table 1.
Discussion
We would like to briefly discuss the imperfections of our quantum repeater protocol. The photon loss is the main imperfection, which is also of crucial importance for the previous quantum repeaters with photon interference8,9,10,11,12,13,14,15,17,18,19,20,21,22,23,24,25. The photon loss happens, due to the fiber absorbtion, diffraction, the cavity imperfection and the inefficiency of the single-photon detectors. It will decrease the success probability and prolong the time needed for establishing the quantum repeater. Since the memory node in this protocol is implemented with the atomic ensemble, the local operation between two collective quantum states  and
and  of the memory node, can be performed with collective laser manipulations35, while excitations of higher-order collective states can be suppressed efficiently with the Rydberg blockade38. During the entanglement swapping process, to detect the collective state of two ensembles in the centering nodes, fluorescent detection44 can be used, since the detection efficiencies of 99.99% for trapped ions have been experimentally demonstrated45. Moreover, with the current significant progress on the source of entangled photon pairs, the repetition rate as high as 106/107 S−1 has been achieved46, so our entanglement distribution process can be performed with a high efficiency.
of the memory node, can be performed with collective laser manipulations35, while excitations of higher-order collective states can be suppressed efficiently with the Rydberg blockade38. During the entanglement swapping process, to detect the collective state of two ensembles in the centering nodes, fluorescent detection44 can be used, since the detection efficiencies of 99.99% for trapped ions have been experimentally demonstrated45. Moreover, with the current significant progress on the source of entangled photon pairs, the repetition rate as high as 106/107 S−1 has been achieved46, so our entanglement distribution process can be performed with a high efficiency.
In summary, we have proposed a high-efficiency quantum repeater with atomic ensembles embedded in optical cavities as the memory nodes, assisted by single-photon faithful transmission. By encoding the polarization qubit into the time-bin qubit, our faithful single-photon transmission can be completed with only linear-optical elements and neither time-slot discriminator nor fast PCs is required29,30,31,32,33. The heralded entanglement creation between the neighboring nodes is achieved with a CPF gate between the atomic ensemble and the photon input in each node, which makes our scheme more convenient than the one with post selection35, although both efficiencies of our quantum repeaters are identical and maximal among all the exciting quantum repeater schemes when multi-mode speed up is not considered18,20. Besides, no additional classical information is involved to determinate the state of the entangled atomic ensembles, since the parties can create a deterministic entanglement up to a feedback upon the results of photon detection. The quantum swapping process is deterministically completed with a simplified PCG involving only one input-output process, which makes our scheme far more efficient than the ones based on linear optical elements15.
Methods
Faithful single-photon transmission
Our protocol for deterministic polarization-error-free single-photon transmission can be details as follows. Assuming the initial state of the single photon to be transmitted is  (|μ|2 + |ν|2 = 1). After passing through the encoder, the photon launched into the noisy channel evolves into
(|μ|2 + |ν|2 = 1). After passing through the encoder, the photon launched into the noisy channel evolves into

where the subscripts l and s represent the photons passing through the long path and short path of the encoder, respectively. When the optical path difference between l and s is small, the two time bins are so close that they suffer from the same fluctuation from the optical fiber channels3,6,29,30,31,32,33,47,48,49,50,51,52. The noise of the channel can be expressed with a unitary transformation UC as follows:

where |δ|2 + |η|2 = 1. After the photon passes through the channels, a π phase shifter Pπ on the d channel is applied and the state of the photon becomes

With a decoder composed of a BS, an HWP and a PBS, shown in Fig. 5(b), the evolution of the photon can be described as follows:

Here the subscripts ls (sl) represent the photon that passes through the long (short) path of the encoder and the short (long) path of the decoder, respectively. The difference between the long path and the short one for the encoder is designed to be the same as that for the decoder. Without any time-slot discriminator, one can get the error-free photon in either the output a1 or a2 at a deterministic time slot.
Performance of CPF and PCG with current experimental parameters
Before we analyze the fidelity of the quantum entanglement distribution and entanglement swapping in our quantum repeater scheme, we first discuss the practical performance of the CPF gate and the PCG based on the recent experiment advances53,54,55. We define the fidelity of a quantum process (or a quantum gate) as  , where
, where  and
and  are the output states of the quantum system in the quantum process (or the quantum gate) in the ideal condition and the realistic condition, respectively15.
are the output states of the quantum system in the quantum process (or the quantum gate) in the ideal condition and the realistic condition, respectively15.
By combining a fibre-based cavity with the atom-chip technology, Colombe et al.53 demonstrated the strong atom-field coupling in a recent experiment in which each 87Rb atom in Bose-Einstein condensates is identically and strongly coupled to the cavity mode. In this experiment, all the atoms are initialized to be the hyperfine zeeman state  . The dipole transition of 87Rb
. The dipole transition of 87Rb 

 is resonantly coupled to the cavity mode with the maximal single-atom coupling strength g0 = 2π × 215 MHz. Meanwhile, the cavity photon decay rate is κ = 2π × 53 MHz and the atomic spontaneous emission rate of
is resonantly coupled to the cavity mode with the maximal single-atom coupling strength g0 = 2π × 215 MHz. Meanwhile, the cavity photon decay rate is κ = 2π × 53 MHz and the atomic spontaneous emission rate of  is γ = 2π × 3 MHz. The whispering-gallery microcavities (WGMC)56 might be another potential experimental realization of our scheme. The parity-time-symmetry breaking is realized in a system of two directly coupled WGMC57 and the controlled loss is also achieved with WGMC58, which enables the on-chip manipulation and control of light propagation. In addition, the routing of single photons has been demonstrated by the atom-WGMC coupled unit controlled by a single photon59.
is γ = 2π × 3 MHz. The whispering-gallery microcavities (WGMC)56 might be another potential experimental realization of our scheme. The parity-time-symmetry breaking is realized in a system of two directly coupled WGMC57 and the controlled loss is also achieved with WGMC58, which enables the on-chip manipulation and control of light propagation. In addition, the routing of single photons has been demonstrated by the atom-WGMC coupled unit controlled by a single photon59.
Under an ideal condition, the reflection coefficients of the input-output processes are  and
and  . In this time, the input
. In this time, the input  polarized photon a will get a π phase shift when the embedded atomic ensemble EA is in the state
polarized photon a will get a π phase shift when the embedded atomic ensemble EA is in the state  ; otherwise, there is no phase shift on the photon a. The fidelity of both the CPF gate (shown in Fig. 4(a)) and the PCG (shown in Fig. 4(b)) can reach unity. In a realistic atom-cavity system, the relationship between the input and output field is outlined in Eqs (3) and (4). In this time, after the party operates the photon a and the ensemble EA with the CPF gate, the output state of the composite system becomes
; otherwise, there is no phase shift on the photon a. The fidelity of both the CPF gate (shown in Fig. 4(a)) and the PCG (shown in Fig. 4(b)) can reach unity. In a realistic atom-cavity system, the relationship between the input and output field is outlined in Eqs (3) and (4). In this time, after the party operates the photon a and the ensemble EA with the CPF gate, the output state of the composite system becomes

Here the normalized coefficient C = |r0 ⋅ μ′ ⋅ μ|2 + |r ⋅ ν′ ⋅ μ|2 + |μ′ ⋅ ν|2 + |ν′ ⋅ ν|2. The fidelity of the CPF gate  depends on the input state of the system composed of the photon and the atomic ensemble. In the symmetric case with
depends on the input state of the system composed of the photon and the atomic ensemble. In the symmetric case with  , the fidelity Fcpf can be simplified to be
, the fidelity Fcpf can be simplified to be

Meanwhile, the efficiency ηcpf of the CPF gate, which is defined as the probability that the photon clicks either detectors after being reflected by the CPF gate, can be detailed as

In a realistic condition, the output state of the composite system composed of a, EA and EB in the PCG process before the single photon is detected becomes

Compared with the ideal output state described in Eq. (7), if an  polarized photon is detected, the fidelity of the PCG gate Fpcg can be expressed as
polarized photon is detected, the fidelity of the PCG gate Fpcg can be expressed as

When the photon in the state  is detected, the fidelity of the PCG is
is detected, the fidelity of the PCG is  . The success of the PCG is heralded when a single photon is detected after the parity-check process, no matter what the state the photon evolves to be. The efficiency ηpcg of the PCG process can be defined as the probability that the probe photon is detected after it is reflected by the two cavities, that is,
. The success of the PCG is heralded when a single photon is detected after the parity-check process, no matter what the state the photon evolves to be. The efficiency ηpcg of the PCG process can be defined as the probability that the probe photon is detected after it is reflected by the two cavities, that is,

Since the absolute value of the relative phase shift during the input-output process depends on the frequency of the input photon, it decreases smoothly with the detuning δ′ between the input photon and the cavity mode, shown in Fig. 3.
The fidelity of the CPF gate Fcpf changes with the detuning δ′, shown in Fig. 7(a). Here the parameters are chosen as g/κ = 2.0283 or 4.0566 and γ/κ = 0.056653. When the linewidth of the input photon is δ = 2|δ′|max with the maximal detuning |δ′|max = 0.5γ (γ), Fcpf is larger than Fcpf(|δ′|max) = 0.9974 (0.9906) for g/κ = 4.0566.
(a) Fidelities of our CPF gate and PCG vs the scaled detuning.  and
and  is performed with the scaled coupling rate g/κ = 2.0283 and γ/κ = 0.0566, Fcpf and Fpcg are performed with the scaled coupling rate g/κ = 4.0566 and γ/κ = 0.056653. (b) Fidelities of our CPF gate and PCG gate vs the scaled coupling rate.
is performed with the scaled coupling rate g/κ = 2.0283 and γ/κ = 0.0566, Fcpf and Fpcg are performed with the scaled coupling rate g/κ = 4.0566 and γ/κ = 0.056653. (b) Fidelities of our CPF gate and PCG gate vs the scaled coupling rate.  and
and  are performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, Fcpf and Fpcg is performed with δ′/κ = γ/κ = 0.0566.
are performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, Fcpf and Fpcg is performed with δ′/κ = γ/κ = 0.0566.
The fidelity of the PCG depends on the coupling rate g/κ, as shown in Fig. 7(b) with the detuning |δ′|max = 0.5 γ or γ. When the maximal detuning of the input photon is |δ′|max = 0.5 γ, the high-performance parity-check gate can be achieved with the fidelity Fpcg higher than Fpcg(|δ′|max) = 0.9944 and 0.9938 for g/κ = 2.0283 and g/κ = 4.0566, respectively.
The efficiencies of the CPF gate and the PCG process versus the coupling rate g/κ are shown in Fig. 8. When the bandwidth of the probe photon is on the scale of γ, both efficiencies ηcpf and ηpcg are robust to the variation of g/κ with the parameters above53. In detail, when the maximal detuning |δ′|max of the input photon is less than 0.5 γ, ηcpf and ηpcg are higher than 0.9966 and 0.9932, respectively. When |δ′|max = γ, ηcpf = 0.9991 and ηpcg = 0.9983 are achievable.
Performance of entanglement distribution and entanglement swapping
Now, let us discuss the fidelities and the efficiencies of the entanglement distribution and entanglement swapping in our quantum repeater scheme. After Alice performs the local operations on the photon a and detects an  polarized photon, the composite system composed of the photon b and the ensembles EA and EB will be projected into the state
polarized photon, the composite system composed of the photon b and the ensembles EA and EB will be projected into the state  , instead of
, instead of  . Here
. Here

where the normalized coefficient C = 2[|r0 − 1|2 + |r0 + 1|2 + |r − 1|2 + |r + 1|2]. And then, the same operations, i.e., a CPF gate sandwiched by two Hadamard operations, are performed by Bob on the photon b. After these operations, the state of the composite system composed of the photon b and the two ensembles EA and EB evolves into

where the normalized coefficient  . One can obtain the fidelity of the entanglement distribution process Fmh and Fmv for the cases that D′h and D′v at the Bob’s node are clicked, respectively.
. One can obtain the fidelity of the entanglement distribution process Fmh and Fmv for the cases that D′h and D′v at the Bob’s node are clicked, respectively.

If one defines the efficiency  as the probability that Alice detects an
as the probability that Alice detects an  polarized photon while Bob detects a photon in either
polarized photon while Bob detects a photon in either  or
or  polarization, one has
polarization, one has

In the above discussion, we detail the performance of our entanglement distribution conditioned on the detection of an  polarization photon at Alice’s node. Considering the symmetric property of the system, one can easily obtain the performance of the entanglement distribution upon the detection of a
polarization photon at Alice’s node. Considering the symmetric property of the system, one can easily obtain the performance of the entanglement distribution upon the detection of a  polarization photon at Alice’s node. Now, the fidelities
polarization photon at Alice’s node. Now, the fidelities  and
and  for the cases that D′h and D′v are clicked at Bob’s node, have the following relations to that for the cases that an
for the cases that D′h and D′v are clicked at Bob’s node, have the following relations to that for the cases that an  polarized photon is detected by Alice,
polarized photon is detected by Alice,  and
and  , see Eq. (30) for detail. Meanwhile, the efficiency
, see Eq. (30) for detail. Meanwhile, the efficiency  of the entanglement distribution process when Alice detects a photon in
of the entanglement distribution process when Alice detects a photon in  polarization is identical to
polarization is identical to  . The total efficiency ηm of the entanglement distribution can be written as
. The total efficiency ηm of the entanglement distribution can be written as

In our entanglement swapping process, two PCGs are applied on the two ensembles  and
and  at the middle node. In fact, only one PCG is enough if a single-atomic-ensemble measurement on each of the two ensembles EB1 and EB2 is utilized after the local Hadamard operations. After these measurements, the system composed of the two remote ensembles EA and EC is in the state
at the middle node. In fact, only one PCG is enough if a single-atomic-ensemble measurement on each of the two ensembles EB1 and EB2 is utilized after the local Hadamard operations. After these measurements, the system composed of the two remote ensembles EA and EC is in the state  with or without a local unitary operation. When the fluorescent measurement44 or field-ionizing the atoms28 with the help of Rydberg excitation are used, the state detection on atomic ensembles could be performed with a near-unity efficiency. In other words, the fidelity of the quantum entanglement swapping process can equal to that of the PCG operation.
with or without a local unitary operation. When the fluorescent measurement44 or field-ionizing the atoms28 with the help of Rydberg excitation are used, the state detection on atomic ensembles could be performed with a near-unity efficiency. In other words, the fidelity of the quantum entanglement swapping process can equal to that of the PCG operation.
The fidelities of both the entanglement distribution and the entanglement swapping in our repeater scheme are shown in Fig. 9. One can see that all Fmh, Fmv and Fs = Fpcg are larger than 0.9936 with the parameters (g, κ, γ) = 2π × (215, 53, 3) MHz achieved in experiment53. Meanwhile, all efficiencies involved in our quantum repeater protocol, shown in Fig. 10, can be larger than 0.9931 when the effective coupling g/κ > 2.0283 with δ′/κ = γ/κ = 0.0566. In a recent experiment with a fiber-based Fabry-Perot cavity constituted by CO2 laser-machined mirrors60, the maximal coupling strength as high as g = 2π × 2.8 GHz is achieved for single Rb atoms and the cavity decay rate is κ = 2π × 0.286 GHz ≃95γ. In this time, g/κ = 9.79 is achieved and a better performance of our scheme is attainable.
Additional Information
How to cite this article: Li, T. and Deng, F.-G. Heralded high-efficiency quantum repeater with atomic ensembles assisted by faithful single-photon transmission. Sci. Rep. 5, 15610; doi: 10.1038/srep15610 (2015).
References
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895 (1993).
Ekert, A. K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991).
Li, X. H., Deng, F. G. & Zhou, H. Y. Efficient quantum key distribution over a collective noise channel. Phys. Rev. A 78, 022321 (2008).
Long, G. L. & Liu, X. S. Theoretically efficient high-capacity quantum-key-distribution scheme. Phys. Rev. A 65, 032302 (2002).
Deng, F. G., Long, G. L. & Liu, X. S. Two-step quantum direct communication protocol using the Einstein-Podolsky-Rosen pair block. Phys. Rev. A 68, 042317 (2003).
Gisin, N., Ribordy, G., Tittel, W. & Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 74, 145 (2002).
Briegel, H. J., Dur, W., Cirac, J. I. & Zoller, P. Quantum repeaters:the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932 (1998).
Childress, L., Taylor, J. M., SØrensen, A. S. & Lukin, M. D. Fault-tolerant quantum communication based on solid-state photon emitters. Phys. Rev. Lett. 96, 070504 (2006).
Simon, C. et al. Quantum communication with quantum dot spins. Phys. Rev. B 75, 081302(R) (2007).
Van Loock, P., Lütkenhaus, N., Munro, W. J. & Nemoto, K. Quantum repeaters using coherent-state communication. Phys. Rev. A 78, 062319 (2008).
Wang, T. J., Song, S. Y. & Long, G. L. Quantum repeater based on spatial entanglement of photons and quantum-dot spins in optical microcavities. Phys. Rev. A 85, 062311 (2012).
Wang, C., Wang, T. J. & Zhang, Y. Construction of a quantum repeater based on a quantum dot in an optical microcavity system. Laser Phys. Lett. 11, 065202 (2014).
Sangouard, N., Dubessy, R. & Simon, C. Quantum repeater based on single trapped ions. Phys. Rev. A 79, 042340 (2009).
Bruschi, D. E., Barlow, T. M., Razavi, M. & Beige, A. Repeat-until-success quantum repeaters. Phys. Rev. A 90, 032306 (2014).
Sangouard, N., Simon, C., de Riedmatten, H. & Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33 (2011).
Raymer, M. G., Walmsley, I. A., Mostowski, J. & Sobolewska, B. Quantum theory of spatial and temporal coherence properties of stimulated raman scattering. Phys. Rev. A 32, 332 (1985).
Duan, L. M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413 (2001).
Simon, C. et al. Quantum repeaters with photon pair sources and multimode memories. Phys. Rev. Lett. 98, 190503 (2007).
Sangouard, N. et al. Long-distance entanglement distribution with single-photon sources. Phys. Rev. A 76, 050301 (2007).
Collins, O. A., Jenkins, S. D., Kuzmich, A. & Kennedy, T. A. B. Multiplexed memory-insensitive quantum repeaters. Phys. Rev. Lett. 98, 060502 (2007).
Zhao, B. et al. Robust creation of entanglement between remote memory qubits. Phys. Rev. Lett. 98, 240502 (2007).
Chen, Z. B. et al. Fault-tolerant quantum repeater with atomic ensembles and linear optics. Phys. Rev. A. 76, 022329 (2007).
Sangouard, N. et al. Robust and efficient quantum repeaters with atomic ensembles and linear optics. Phys. Rev. A 77, 062301 (2008).
Lin, G. W., Zou, X. B., Lin, X. M. & Guo, G. C. Long-distance quantum communication with individual atoms and atomic ensembles. Phys. Rev. A 79, 042332 (2009).
Hong, F. Y. & Xiong, S. J. Robust quantum repeater with atomic ensembles and single-photon sources. Phys. Rev. A 79, 052341 (2009).
Lukin, M. D. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett. 87, 037901 (2001).
Han, Y. et al. Quantum repeaters based on Rydberg-blockade-coupled atomic ensembles. Phys. Rev. A 81, 052311 (2010).
Zhao, B., Múller, M., Hammerer, K. & Zoller, P. Efficient quantum repeater based on deterministic Rydberg gates. Phys. Rev. A 81, 052329 (2010).
Li, X. H., Deng, F. G. & Zhou, H. Y. Faithful qubit transmission against collective noise without ancillary qubits. Appl. Phys. Lett. 91, 144101 (2007).
Gao, M., Liang, L. M., Li, C. Z. & Wang, X. B. Robust quantum repeater with atomic ensembles against phase and polarization instability. Phys. Rev. A 79, 042301 (2009).
Yin, Z. Q. et al. Quantum repeaters free of polarization disturbance and phase noise. Phys. Rev. A 79, 044302 (2009).
Zhang, B. B. & Xu, Y. Q. Atomic-ensemble-based quantum repeater against general polarization and phase noise. Phys. Rev. A 84, 014304 (2011).
Kalamidas, D. Linear optical scheme for error-free entanglement distribution and a quantum repeater. Phys. Rev. A 73, 054304 (2006).
Mei, F., Feng, M., Yu, Y. F. & Zhang, Z. M. Scalable quantum information processing with atomic ensembles and flying photons. Phys. Rev. A 80, 042319 (2009).
Brion, E., Carlier, F., Akulin, V. M. & Mølmer, K. Quantum repeater with Rydberg-blocked atomic ensembles in fiber-coupled cavities. Phys. Rev. A 85, 042324 (2012).
Wang, T. J., Liu, L. L., Zhang, R., Cao, C. & Wang, C. One-step hyperentanglement purification and hyperdistillation with linear optics. Opt. Express 23, 9284–9294 (2015).
Zhou, L. & Sheng, Y. B. Recyclable amplification protocol for the single-photon entangled state. Laser Phys. Lett. 12, 045203 (2015).
Brion, E., Mølmer, K. & Saffman, M. Quantum computing with collective ensembles of multilevel systems. Phys. Rev. Lett. 99, 260501 (2007).
Saffman, M. & Walker, T. G. Creating single-atom and single-photon sources from entangled atomic ensembles. Phys. Rev. A 66, 065403 (2002).
Rui, J., Jiang, Y., Zhao, B., Bao, X. H. & Pan, J. W. Arbitrary rotation of a single spinwave qubit in an atomic-ensemble quantum memory. arXiv: 1501.07067v1 (2015).
Walls, D. F. & Milburn, G. J. Quantum Optics (Springer-Verlag, Berlin, 1994).
Duan, L. M. & Kimble, H. J. Scalable photonic quantum computation through cavity-assisted interaction. Phys. Rev. Lett. 92, 127902 (2004).
Xiao, Y. F. et al. Realizing quantum controlled phase flip through cavity QED. Phys. Rev. A 70, 042314 (2004).
Brask, J. B. et al. Fast entanglement distribution with atomic ensembles and fluorescent detection. Phys. Rev. A 81, 020303(R) (2010).
Myerson, A. H. et al. High-fidelity readout of trapped-ion qubits. Phys. Rev. Lett. 100, 200502 (2008).
Fulconis, J. et al. High brightness single mode source of correlated photon pairs using a photonic crystal fiber. Opt. Express 13, 7572 (2005).
Simon, C. & Pan, J. W. Polarization entanglement purification using spatial entanglement. Phys. Rev. Lett. 89, 257901 (2002).
Sheng, Y. B. & Deng, F. G. Deterministic entanglement purification and complete nonlocal Bell-State analysis with hyperentanglement. Phys. Rev. A 81, 032307 (2010).
Sheng, Y. B. & Deng, F. G. One-step deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 82, 044305 (2010).
Deng, F. G. One-step error correction for multipartite polarization entanglement. Phys. Rev. A 83, 062316 (2011).
Li, X. H. Deterministic polarization-entanglement purification using spatial entanglement. Phys. Rev. A 82, 044304 (2010).
Sheng, Y. B. & Zhou, L. Deterministic entanglement distillation for secure double-server blind quantum computation. Sci. Rep. 5, 7815 (2015).
Colombe, Y. et al. Strong atom-field coupling for Bose-Einstein condensates in an optical cavity on a chip. Nature 450, 272 (2007).
Volz, J. et al. Measurement of the internal state of a single atom without energy exchange. Nature 475, 210 (2011).
Ritsch, H., Domokos, P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 85, 553–601 (2013).
Peng, B. et al. What is and what is not electromagnetically induced transparency in whispering-gallery microcavities. Nat. Commun. 5, 5082 (2014).
Peng, B. et al. Parity-time-symmetric whispering-gallery microcavities. Nat. Phys. 10, 394–398, (2014).
Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332, (2014).
Shomroni, I. et al. All-optical routing of single photons by a one-atom switch controlled by a single photon. Science 345, 903–906, (2014).
Hunger, D. et al. A fiber Fabry-Perot cavity with high finesse. New J. Phys. 12, 065038 (2010).
Acknowledgements
TL was supported by the China Postdoctoral Science Foundation under Grant No. 2015M571011. FG was supported by the National Natural Science Foundation of China under Grant Nos. 11174039 and 11474026, the Fundamental Research Funds for the Central Universities under Grant No. 2015KJJCA01 and the Open Foundation of State key Laboratory of Networking and Switching Technology (Beijing University of Posts and Telecommunications) under Grant No. SKLNST-2013-1-13.
Author information
Authors and Affiliations
Contributions
T.L. completed the calculation. T.L. and F.G. prepared the figures and wrote the main manuscript text. F.G. supervised the whole project. Both authors reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Li, T., Deng, FG. Heralded high-efficiency quantum repeater with atomic ensembles assisted by faithful single-photon transmission. Sci Rep 5, 15610 (2015). https://doi.org/10.1038/srep15610
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep15610
- Springer Nature Limited
This article is cited by
-
Entanglement Purification on Separate Atoms in an Error-Detected Pattern
International Journal of Theoretical Physics (2019)
-
Robust Deterministic Controlled Phase-Flip Gate and Controlled-Not Gate Based on Atomic Ensembles Embedded in Double-Sided Optical Cavities
International Journal of Theoretical Physics (2018)
-
Efficient Entanglement Concentration of Nonlocal Two-Photon Polarization-Time-Bin Hyperentangled States
International Journal of Theoretical Physics (2018)
-
Schemes generating entangled states and entanglement swapping between photons and three-level atoms inside optical cavities for quantum communication
Quantum Information Processing (2017)
-
High-dimensional Controlled-phase Gate Between a 2 N -dimensional Photon and N Three-level Artificial Atoms
International Journal of Theoretical Physics (2017)


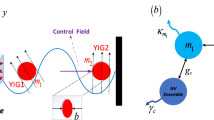





 polarized photon and reflects the
polarized photon and reflects the  component. HWP1 and HWP2 are half-wave plates performing the bit-flip operation, while H represent a Hadamard rotation.
component. HWP1 and HWP2 are half-wave plates performing the bit-flip operation, while H represent a Hadamard rotation.



 and
and  is performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, ηcpf and ηpcg are performed with δ′/κ = γ/κ = 0.0566.
is performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, ηcpf and ηpcg are performed with δ′/κ = γ/κ = 0.0566.

 and
and  is performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, ηm and ηs are performed with δ′/κ = γ/κ = 0.0566.
is performed with the scaled detuning δ′/κ = 0.0283 and γ/κ = 0.0566, ηm and ηs are performed with δ′/κ = γ/κ = 0.0566.