Introduction

Spin-orbit coupling (SOC) describes an intrinsic interaction between the spin and the momentum of a particle. SOC plays a major role in condensed matter systems, such as spin and anomalous Hall effects1,2, topological insulators and topological superconductors3. Recently it is found that SOC also plays a key role in realizing spintronics4 and topological quantum computing5. However, the SOC physics in typical solid-state materials is hard to observe because the strength of the SOC is generally much smaller than the Fermi velocity of electrons. Quantum many-body systems of ultra-cold atom gases can be precisely controlled in experiments and would thus provide an ideal platform to explore novel SOC physics and device applications6. Recently, SOC with equal Rashba and Dresselhaus strength has been realized in a neutral atomic Bose-Einstein condensate (BEC) by dressing two atomic spin states with a pair of Raman lasers7. Moreover, such SOC strength is much stronger than that in typical solid-state materials. With the strong strength of SOC, spins are not conserved during their motion and rich exotic superfluid phenomena have been revealed8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31. For instance, new topological excitations and new ground state phases have been observed in spin-orbit coupled Fermi gases and BEC, respectively32,33,34,35,36,37,38. Here we study the spin and the field (bosonic) squeezing in the system of ultracold atoms in the trapped BEC with the equal Rashba and Dresselhaus SOCs.

Spin squeezing39,40,41,42, arising from quantum correlations of collective spin systems, has potential applications in quantum information processes, quantum metrology and atom interferometers43,44. It is also closely related to quantum entanglement45,46,47,48. In the past few years, many efforts have been devoted to the generation of squeezing in atomic systems. In recent experiments, it has been reported that spin squeezing can be generated in a ensemble of atoms via atom-photon interactions or a BEC via atom collisions49,50,51,52.

In this work, we investigate properties of the ground state of a spin-orbit coupled BEC and show that both spin and field squeezing can be induced by the SOC in the BEC. First, we map the spin-orbit coupled BEC to the well-known quantum Dicke model and show that there exists a quantum phase transition (QPT) from a superradiant (spin polarized) to normal (spin balanced) phase by tuning two Raman lasers with a current experimental setup of National Institute of Standards and Technology (NIST). In the superradiant phase, macroscopic spin polarization and occupation number of harmonic trap mode are presented. By contrast, in the normal phase, the values of spin polarization and occupation number of harmonic trap mode become zero. The behaviors of spin and field squeezing near the critical point are also explored. It is found that, at the critical point, the maximal spin squeezing is achieved and a sudden transition occurs for the field squeezing, which can indicate the QPT. In addition, the field squeezing is independent of the SOC strength in this phase. We also discuss the effects of the detuning on the ground state of spin polarization and quasi-momentum and show the results agree with those in recent experiments18. The presence of the detuning suppresses the spin and field squeezing, while it enhances the occupation number of harmonic trap mode.

Results

Model and quantum phase transition

In a recent benchmark experiment, the equal Rashba and Dresselhaus SOCs were realized in the trapped BEC with 87Rb atoms7, as illustrated in Fig. 1(a), all ultracold atoms are prepared in a two dimensional BEC in the xy plane with a strong confinement along the z axis. Such a two dimensional setup does not affect the essential physics, since the z direction is decoupled with the SOC. With a large detuning Δ from the excited state, the hyperfine ground state |F = 1, mF = −1〉 and |F = 1, mF = 0〉 can be defined as effective spin-↑ and spin-↓ respectively, which is shown in Fig.1 (b). In the dressed state basis and with k1 and k2 denoting the wave vectors of the Raman lasers, equal Rashba and Dresselhaus SOCs can be induced by two Raman lasers incident at a π/4 angle from the x axis and the corresponding dynamics of single particle of the BEC is governed by the following nonlinear Gross-Pitaevskii (GP) equation

where Ψ = (ψ↑, Ψ↓)T is the wavefunction on the dressed state basis and satisfies the normalization condition , p is the momentum and is the harmonic trap potential with m being the mass of the ultracold atom and ωx,y denoting the trapping frequencies in the x, y axes. In addition, the Hamiltonian Hs describing the equal Rashba and Dresselhaus SOCs is given by

where σx and σz are the Pauli matrices, describes the SOC strength with λ denoting the wave length of the Raman lasers, Ω measures the Raman coupling strength and δ is the detuning from the level splitting. The many-body interaction Hamiltonian is HI = diag(g↑↑|Ψ↑|2 + g↑↓|Ψ↓|2, g↑↓|Ψ↑|2 + g↓↓|Ψ↓|2), where g↑↑ = g↑↓ = and g↓↓ = represent the inter- and intra-spin collision interactions, respectively. Here, c0 and c2 are the s-wave scattering lengths, N is the atom number and with the trapping frequency ωz in the z axis.

Figure 1
figure 1

Illustration about the model and the level diagram.

(a) The experimental scheme for realizing the equal Rashba and Dresselhaus SOC in the trapped BEC. (b) Level diagram: three hyperfine states |−1〉, |0〉 and |1〉 are coupled by the Raman lasers.

Full size image

In the present experiment, the s-wave scattering lengths have been measured as c0 = 100.86aB and c2 = −0.46aB, where aB is the Bohr radius. Then we can find g↑↑ = g↑↓ ≈ g↓↓. Introducing the harmonic mode operators, and , the Hamiltonian (1) for N particles can be mapped to a Dicke type model16,17,18

where and are the collective spin operators. Since the boson mode in the y direction does not interact with the ultracold atom, the system can be reduced to

When δ = 0, the Hamiltonian is equivalent to the standard Dicke model53. Here, we shall note that if the repulsive interaction between the different spin components is sufficiently strong, the mapping to the Dicke model is invalid, which is due to the fact that the trapped BEC is unstable when . In contrast, if there is no interaction between the trapped BEC, there will be no correlation between the ultracold atoms and all of the ultracold atoms will occupy both in the momentum space. Then, the single spatial mode approximation which we have used is not valid.

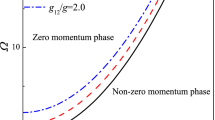
For the system with Hamiltonian (4), there is a quantum phase transition between the normal phase and the superradiant phase by changing the Raman coupling strength Ω. By means of the mean field coherent state approach, the critical point for the phase transition of the system can be obtained. We assume the wave function of the ground state is given by |ψ〉 = |θ〉 : |α〉, where |θ〉 is the spin coherent state and |α〉 is the spatial coherent state with a |α〉 = α |α〉 and α = u + iv. In the absence of the detuning term, i.e., δ = 0, the energy of the system is (with the constant dropped)

Minimizing the energy E with respect to θ, the critical point is given by Ωc = , where is the recoil energy. When Ω > Ωc, the system is in the spin-balanced normal phase, where the spin polarization and the occupation number of harmonic trap mode are zero. In the region Ω < Ωc, the ground state has two degenerate local minima with spin polarization and the occupation number of harmonic trap mode . As is shown in Fig. 2, the spin polarization 〈Sz〉 and rescaled occupation number of harmonic trap mode as functions of Ω are plotted in the resonance case (δ = 0). The direct numerical results respect to Hamiltonian (4) agree well with those by the mean field approximation. In the superradiant phase, the system has a macroscopic occupation number of harmonic trap mode and spin polarization which coincides well with the results in the recent experiment18. In contrast, in the normal phase, there are no occupation number of harmonic trap mode and spin polarization. As a consequence, either the spin polarization or the occupation number of harmonic trap mode can be considered as an order parameter of QPT.

Figure 2
figure 2

Quantum phase transition in terms of spin polarization and occupation number.

(a) Spin polarization and (b) occupation number of harmonic trap mode as a function of Ω. The red squares are analytical results for the mean field and blue lines are the numerical results from the Hamiltonian (4). The parameters are chosen as m = 1.44 × 10−25 kg, λ = 804.1 nm, ωx = 2π × 50 Hz and N = 4 × 103.

Full size image

Spin and field squeezing

Now we discuss the applications of the spin-orbit coupled BECs in quantum information science. Spin squeezing has potential application in atom interferometers and high precision atom clocks. It can also signify long-range quantum correlations. Spin squeezing can be quantified by the following parameter39

with . The subscript n⊥ refers to an arbitrary axis perpendicular to the mean spin S. The inequality ξ2 < 1 indicates the state is spin squeezed.

For the bosonic squeezing, it can be characterized by a parameter

where Xθ = X cos θ + P sin θ with X = a + a† and P = i(a† − a). For the special case, θ = π/2, ζ2 = (Δpx)2, it means the field squeezing of the system corresponds to the momentum squeezing. For a quantum state, the field squeezing factor can also be written as54,55,56

As is shown in Fig. 3, the spin and field squeezing factors as functions of Ω with δ = 0 are plotted. It is demonstrated that the spin squeezing parameter attains its minimal value at the boundary between the normal and superradiant phases. For the bosonic squeezing factor, it decreases as Ω increases, which indicates the system exhibits a bosonic squeezing when Ω ≠ 0.

Figure 3
figure 3

Quantum phase transition in terms of spin and field squeezing parameters.

(a) Spin squeezing parameter ξ2 and (b) bosonic squeezing factor ζ2 as functions of Ω. The red square denotes the analytical result in Eqs. (10) and (13), whereas the blue lines reflects the direct numerical results of Hamiltonian (4). The parameters are the same as those in Fig. 2.

Full size image

For the above squeezing phenomenon, a natural question arises as how the system exhibits the spin and field squeezing. In Hamiltonian (4), we can not directly find the spin-spin interaction. In fact, both the spin and field squeezing can be induced by SOC. To demonstrate these arguments clearly, we employ a unitary transformation U = exp(iG(a† + a)Sz) with to rewrite Hamiltonian (4) as HU = U†HTU17. After a straightforward calculation, we can obtain

For such a Hamiltonian, we can clearly see that the system shows the spin-spin interaction and nonlinear terms of harmonic trap mode from the terms and cos[G(a† + a)] − sin[G(a† + a)], respectively. Thus we can argue that the spin-orbit coupling induces the spin and field squeezing.

To derive an analytical result of spin squeezing factor, we need to reduce the terms cos[G(a† + a)] − sin[G(a† + a)]. For a large number of atom, we have and thus . In fact the occupation number 〈a†a〉 of harmonic trap mode is inversely proportional to ωxN16, which indicates the negligible term sin[G(a† + a)] ~ 0 and the term . Then the Hamiltonian HU can be reduced to , which corresponds to the Lipkin-Meshkov-Glick model. Treating the quantum effects as small fluctuations, an approximate result of ξ2 can be obtained by using the Holstein-Primakoff transformation in the limit of large atom number. Introducing the Holstein-Primakoff transformation and and using the Bogoliubov transformation57,58, the Hamiltonian can be diagonalized and the spin squeezing parameter can be obtained as (see method)

In the region Ω > Ωc, when , . It is due to the fact that for the large value of Ω, all the spins are polarized along the x axis. In fact, Ω can be tuned from 10−2 kHz to MHz in the current experiment, thus the system always exhibits spin squeezing. As is shown in Fig. 3(a), the numerical result agrees with the approximation analytical result in Eq. (10).

To obtain the result of the bosonic squeezing, we can reduce the Hamiltonian HU to an effective Hamiltonian (with the constant terms neglected)

with and for Ω < Ωc and > Ωc, respectively. In the above derivation, we have used Sx = and −N/2 for Ω < Ωc and > Ωc, respectively. The Hamiltonian can be diagonalized by using the Bogoliubov transformation

with tanh 57,59. For the diagonalization of the Hamiltonian, we can find the ground state in the bosonic vacuum, i.e. , in terms of which the corresponding field squeezing parameter is given by

We note that in the superradiant phase, ζ2 is independent of the SOC strength γ which can be tuned through a fast and coherent modulation of Raman coupling16. As is shown in Fig. 3(b), ζ2 is plotted with different effective SOC strengths. We find the numerical results of Hamiltonian (4) coincide well with the analytical ones in Eq. (13).

Effect of detuning to spin and field squeezing

We proceed to consider the effect of the detuning on the spin polarization and the quasi-momentum. In a recent experiment, the spin polarization and quasi-momentum have been measured by linearly swept the detuning with different Ω18. It has been observed that the phenomenon of QPT vanishes and the BEC is always in the superradiant phase for a finite detuning. As is shown in Fig. 4(a), we investigate the ground state of the spin polarization and the quasi-momentum with Ω = 3ER. We find that the spin polarization and the quasi-momentum exhibit a step jump at δ = 0 as the detuning δ increases. When δ < 0, most of the atoms are in the state |↑〉, as δ increases and δ > 0, most of the ultracold atoms stay at the state |↓〉. These numerical results coincide well with the experiment result18.

Figure 4
figure 4

Effect of the detuning.

(a) Spin polarization (blue line) and quasi-momentum (red line with circles) (b) occupation number of harmonic trap mode Np, (c) spin and (d) field squeezing parameter as a function of Raman detuning δ with Ω = 3ER. The parameters are chosen as m = 1.44 × 10−25 kg, λ = 804.1 nm, ωx = 2π × 100 Hz and N = 2 × 103.

Full size image

The occupation number of harmonic trap mode Np is also studied for the finite detuning. As is shown in Fig. 4(b), Np is plotted as a function of the detuning. We can find that Np increases as the detuning |δ| increases, which means the presence of detuning increases the occupation number of harmonic trap mode. For the spin and field squeezing, shown in Fig. 4(c) and (d), ξ2 and ζ2 increase as the value of |δ| increases, which indicates the presence of detuning suppresses the spin and field squeezing.

Discussion

We have investigated the spin-orbit coupled BEC via spin and field squeezing. By mapping the system to the well-known quantum Dicke model, we show that the quantum phase transition of superradiant (spin polarized)-normal (spin balanced) can be induced by tuning two Raman lasers with a current experimental setup of NIST. Crossing from the normal phase to the superradiant phase, macroscopic spin polarization and occupation number of harmonic trap mode emerge at the critical point. Therefore, the spin polarization and occupation number of harmonic trap mode can be treated as the order parameters revealing the quantum criticality. We further consider the behaviors of spin and field squeezing near the critical point and find that the spin and field squeezings reveal the quantum phase transition in different manners. At the critical point, the maximal spin squeezing (with the minimal squeezing factor) occurs and the field squeezing experiences a sudden transition. In addition, the field squeezing is independent of the SOC strength in the in the superradiant phase. Finally, the effects of the detuning on the ground state of spin polarization and quasi-momentum are studied. The presence of the detuning suppresses the spin and field squeezing, while it enhances the occupation number of harmonic trap mode.

Methods

Here we employ the Holstein-Primakoff and Bogoliubov transformations to derive the result of spin squeezing. In the Sec. II, we obtain a reduced Hamiltonian . For simplicity, we rewrite the form of as which indicates the spin direction along as z axis. Rotating the z axis to the semiclassical magnetization, we obtain57,58

where θ0 = 0 for > 1 and θ0 = arccos() for . Then the corresponding transformed Hamiltonian reads (with the constant terms dropped)

where m = cos θ0. Introducing the Holstein-Primakoff representation

where b† and b satisfy the relation [b, b†] = 1. Then we obtain the Hamiltonian (neglecting the constant terms)

up to the 0th order of N. Using the Bogoliubov transformation

the Hamiltonian can be diagonalized with

When > 1, m = 1 and we can obtain

Then the corresponding spin squeezing parameter is given by

When , m = h, we have

Then we obtain