Introduction

The ability to carry non-dissipative electric currents in strong magnetic fields is one of the fundamental features of type-II superconductors crucial for many applications1,2,3,4,5,6,7,8,9,10. The current, however, exerts a transverse Lorentz force on vortices, leading to their dissipative motion and to finite resistance unless materials defects immobilize (pin) vortices at current densities below some critical value Jc. Pinning potential wells U(r) produced by defects are the key building blocks that determine collective pinning phenomena, in which a flexible vortex line is pinned by multiple defects. The global electromagnetic response of the vortex matter is thus governed by a complex interplay of individual pinning centers, interaction between vortices and thermal fluctuations11. Recent advances in materials science have enabled several groups to controllably produce nanostructures of nonsuperconducting precipitates to optimize the pinning of vortices in superconductors and to achieve Jc up to 10–30% of the fundamental depairing current density Jd at which the current breaks Cooper pairs2,3,4,5,6,7,8,9,10. In artificially-engineered pinning structures, the shape of U(r) can also be made asymmetric to produce the intriguing vortex ratchet and rectification phenomena12,13,14,15,16,17. Local studies of individual vortices using scanning probe techniques18,19,20 based on STM, MFM, Hall probes and SQUIDs have allowed controllable manipulation of single vortices21 and have revealed phase transitions22,23,24, vortex dynamics and pinning at grain boundaries25,26, collective creep of a vortex lattice27,28 and collective motion29,30 and dissipative hopping of individual vortices in response to an ac magnetic field31. Even so, the intrinsic structure of a single pinning potential well U(r), which determines the fundamental interaction of vortices with pinning centers, has not yet been measured directly.

Difficulties with the measurement of U(r) arise from the necessity of deconvoluting the effect of multiple pinning defects along the elastic vortex line and from the lack of experimental techniques for extracting U(r) on the scale of the superconducting coherence length ξ (ranging from 2 to 100 nm for different materials) that quantifies the size of the Cooper pair. To avoid the complexity of the situation in which the vortex line behaves like an elastic string pinned by multiple defects21, the vortex length should to be of the order of ξ. This situation can be achieved in thin superconducting films of thickness in a perpendicular magnetic field. Moreover, in order to simplify the interpretation of experimental data, it is desirable to choose a film in which the three basic length scales of the system are comparable, , where λ is the bulk magnetic penetration depth. We have therefore chosen to study Pb thin films (Tc = 7.2 K) with d = 75 nm, ξ (4.2 K) = 46.4 nm and . In this case, the vortex can be regarded as a particle in a random two-dimensional (2D) potential landscape of pinning defects.

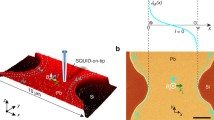
We employed a novel nanoscale superconducting quantum interference device (SQUID) that resides on the apex of a sharp tip32,33 to trace vortex trajectories. A highly sensitive SQUID-on-tip (SOT) with a diameter of 177 nm was integrated into a scanning probe microscope operating at 4.2 K33. Figure 1a shows a scanning magnetic image of a Pb film patterned into an 8 µm wide microbridge in which a single vortex was trapped upon field cooling at about 0.1 mT. A small ac current Iac is applied along the bridge (y direction) resulting in a Lorentz force on the vortex Fac = Φ0Jac along the perpendicular x axis, where Jac is the sheet current density and Φ0 = 2.07×10−15 Wb is the magnetic flux quantum. The weak Fac results in a small oscillation of the vortex around its equilibrium position with typical amplitude of 1 nm, much smaller than ξ. The scanning SOT microscope simultaneously measures the distributions of the dc magnetic field Bdc(x,y) and of the ac field Bac(x,y) at the driving frequency measured by a lock-in amplifier (Figures 1a and 1b). For small displacements of the vortex, the two fields are related by

Using this relation, we measured the ac displacements xac and yac of the vortex along the x and y axes as outlined in Figures 1c to 1g. The very high sensitivity of our SOT allows us to measure sub-atomically-small displacements, down to 10 pm [Figure S7]. Adding a dc current Idc exerts a driving force Fdc = Φ0Jdc that tilts the potential and shifts the vortex equilibrium position. By changing Fdc in small steps, we are able to reconstruct the full vortex ac response xac(Fdc) and yac(Fdc) along the potential well. If the vortex oscillates within a potential well without hopping to neighboring wells, dissipation is negligible and xac and yac are in-phase with Iac.

Figure 1
figure 1

Magnetic imaging of a single vortex.

(a), Scanning SQUID-on-tip image of Bdc(x,y) showing a single vortex (bright) in a thin Pb film patterned into an 8 µm wide microbridge at T = 4.2 K. The microbridge is in the Meissner state (dark) and the enhanced field outside the edges (bright) is due to the screening of the applied field of 0.3 mT. (b), Scanning image of Bac(x,y) acquired simultaneously with (a) showing the vortex response to an ac current of Iac = 0.94 mA peak-to-peak (ptp) at 13.3 kHz applied to the microbridge. The Meissner response is visible along the microbridge (Bac = 0, light brown) with positive (negative) Bac outside the left (right) edge due to the field self-induced by Iac. (c), A zoomed-in image of the measured Bdc(x,y) of a vortex. (d–f), Numerically derived ∂Bdc/∂x, ∂Bdc/∂y and −xac∂Bdc/∂x−yac ∂Bdc/∂y with xac = 1.6 nm and yac = −1.9 nm values obtained by a fit to (g). (g), Experimentally measured Bac(x,y) of the vortex driven by Iac acquired simultaneously with (c).

Full size image

We first analyze the expected response of the vortex trapped in a single potential well modeled by the generic Lorentzian function U(r) = −U0/(1 + (r/ξ)2), where r is the radial distance from a materials defect11,34,35,36 (Figure 2d). Depending on the nature and the size of the defect, the pinning energy U0 is a fraction of the maximum superconducting condensation energy of the vortex core 11, where d = 75 nm is the film thickness, Hc(4.2 K) = 530 Oe is the thermodynamic critical field of Pb and ξ(4.2 K) = 46.4 nm is derived from the measurement of the upper critical field Hc2 = Φ0/2πξ2 (Figure S5). In the absence of current, the vortex is located at the minimum of U(r) at xm = 0. A dc driving force Fdc = Φ0Jdc tilts the potential, Uf(x) = U(x)−Fdcx, displacing the vortex to a new minimum at xm(Fdc), where the driving force is balanced by the restoring force, (Figure 2c). In our experiment, we measure the ac displacement of the vortex which is inversely proportional to the pinning spring constant, k = ∂2U/∂x2. Figure 2a shows that the spring constant k(x) is the stiffest in the center of the well and gradually softens towards the inflection points of U(x) at so that xac(Fdc) progressively increases until the vortex hops out of the well.

Figure 2
figure 2

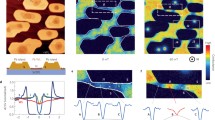
Vortex response and the structure of potential well 2 and comparison to simulations.

(a–d), Calculated vortex response to Fac = 8.89 fN in a potential well U(r) = −U0/(1 + (r/ξ)2) due to a single defect with U0 = 4 eV: (a), vortex ac displacement xac and yac; (b), vortex trajectory; (c), restoring force; and (d), the potential shifted to zero value at its minimum. The data points end where the activation barrier ΔU = 34kBT (see S9). (e–h), Measured vortex response in well 2: (e), displacements xac and yac in response to Fac = 8.89 fN, displaying a large softening peak in the middle of the well; (f), vortex trajectory with an ‘S’ shape; (g), restoring force showing a pronounced inflection point; and (h), the potential well with its minimum set to zero. The data points end where the vortex hopped into a different well. (i–l), Calculated vortex response in a potential well due to a cluster of four defects (see Figure 5a for locations of defects): (i), ac vortex displacement; (j), vortex trajectory; (k), restoring force; and (l), the potential with its minimum set to zero. The data points end where ΔU = 34kBT.

Full size image

By sweeping the driving force Fdc and integrating over xac, the x position of the vortex and the shape of the restoring force Fr(x) = −Fdc(xm) are obtained. Combining these results with the corresponding integration over yac yields the full vortex trajectory ym(Fdc) vs. xm(Fdc) within the well. In an isotropic potential, yac = 0 and the vortex trajectory is a straight line (Figure 2b).

Figure 2e shows the ac displacements xac(Fdc) and yac(Fdc) measured for one of the potential wells (well 2, see Figure 3). Following the above procedure, we derive the vortex trajectory within the well (Figure 2f), the restoring force (Figure 2g) and the single-well pinning potential (Figure 2h). Figure 3 shows a compilation of similar results for different potential wells. These data reveal the following features of vortex response that are strikingly different from the expected behavior shown in Figures 2a–d. (i) Spring softening in the middle of the well. In contrast to Figure 2a, which shows the highest stiffness in the center of the well, Figure 2e reveals a large and sharp peak in xac, which implies a small k and an inflection point in the restoring force in the central region of the well, shown by the arrow in Figure 2g. This intriguing feature turned out to be ubiquitous and various degrees of softening in the middle of the wells were found in the majority of pinning sites as illustrated by Figures 3b and S8d. (ii) Broken-spring phenomenon. The ac response xac(Fdc) is expected to increase progressively towards the edges of the well and diverge at the inflection point of U(x) due to the vanishing spring constant k(x) at the maximum restoring force (Figures 2a and 2c). Surprisingly, Figure 2e shows only a small increase in xac towards the well edges, where the restoring force (Figure 2g) exhibits hardly any rounding at its maximum values. This response resembles the abrupt breaking of an elastic spring. (iii) Anisotropy. In an isotropic well, the vortex moves only in the direction of the driving force (Figures 2a and 2b). However, Figure 2e shows that the vortex also has a significant transverse ac displacement yac and a substantial y component in the trajectory (Figure 2f). Analysis of different wells has shown that the vortex may move at angles as large as 77° with respect to the direction of the driving force (see Figures 3 and S8). (iv) Asymmetry and internal structure. Figures 3c and S8e show that most of the potential wells are asymmetric with respect to the positive and negative driving force and exhibit significant deviations from the model function U(r) = −U0/(1 + (r/ξ)2). In Figure 2h, for example, the well is nearly parabolic at the bottom but has a linear intermediate section that again becomes parabolic at larger negative displacements. Even though the wells appear to be smooth on the scale of ξ, they have an internal structure that results in nontrivial shapes of the restoring forces and intricate trajectories of vortices in the individual wells (Figures 3a–b and S8c–d). Also, a point defect results in a well of width between the inflection points, while many of the observed wells are significantly wider, reaching 110 nm (Figures 3c and S8e). (v) Correlation between softening and the inflection point in the trajectory. We also observed an intriguing correlation between the position of the softening point of the potential, which is the inflection point in the restoring force and the position of the inflection point in the trajectory, as marked by arrows in Figures 2f and 2g. This correlation gives an important clue to the internal structure of the pinning potential and the dynamics of vortices, as described below.

Figure 3
figure 3

Comparison of different potential wells.

(a), Vortex trajectories in wells 1 to 5, shifted vertically for clarity. x = 0 corresponds to the rest position of the vortex at Fdc = 0, except for the metastable well 3 that does not exist at Fdc = 0 (see Figure 4b). All the wells display nontrivial internal structure. (b), The restoring force Fdc = −Fr(x) of the different wells shifted vertically for clarity. x = 0 corresponds to Fdc = 0 for each well except well 3. (c), The structure of the potential of the different wells shifted for clarity.

Full size image

We now examine vortex dynamics on larger scales that include several pinning wells. At each value of Fdc, we acquire a full image of Bdc(x,y) and Bac(x,y) at a constant Fac, compiling a movie of the ac response as Fdc is swept back and forth (See S6). Figures 4e–j show several frames of Bac(x,y) from one of the movies. As Fdc is changed, Bac(x,y) shows significant variations in the intensity and the orientation of the dipole-like signal, reflecting the changes in both amplitude and direction of the ac displacement of the vortex within a single well. If Fdc exceeds the maximum restoring force of a well, the vortex jumps to a different well, manifesting as an instantaneous displacement of the dipole in the movie. By recording the ac displacements in the wells and the jumps between the wells, a full map of closed loops of vortex trajectories was obtained, as shown in Figure 4a (and an additional example in Figure S8a). The corresponding plot of the restoring force is shown in Figure 4b (and S8b). Figure 4a shows that the vortex resides in well 1 at large negative values of Fdc. As the applied force exceeds the maximum restoring force, the vortex may jump all the way to well 5, where it stays up to our maximum Fdc 4.44 pN. As Fdc is decreased, the vortex undergoes a sequence of jumps to wells 4, 3, 2 and eventually back to 1. While the trajectory of the vortex within a well is reversible, the transition between the wells is hysteretic. Thus, to explore all possible intermediate trajectories and transitions, sub-loop sweeps of Fdc were performed. Analysis of the data from repeated sweeps leads to the following additional conclusions about the interaction of vortices with pinning wells: (vi) Hopping distance and direction. While the size of the individual wells is typically (1–2)ξ, the hopping distance between the wells is usually significantly larger, up to 20ξ. The vortex jumps between wells often have large transverse components with respect to the direction of the Lorentz force, as seen in Figure 4a (and S8a). The hopping between wells 3 and 4, for example, occurs at the angle ~ 70° with respect to Fdc. (vii) Metastable wells. Some minima in the pinning potential only appear at a finite dc Lorentz force. For example, well 3 in Figure 4b exists only at negative Fdc and well 6 exists only at positive Fdc. Moreover, Fig. 4b shows that the vortex jumps from well 3 to well 4 in the positive x direction even though the driving force is negative (green dashed line); that is, the vortex moves against the Lorentz force. (viii) “Nondeterministic” hopping. Upon repeating the loops several times, we find that vortex jumps between the wells show significant variability. For example, the force Fdc at which the vortex jumps from well 5 to well 4 is quite different for different dc current sweeps (dashed magenta lines in Fig. 4b). In addition, the vortex occasionally hops from well 5 directly to well 3 instead of well 4. Similarly, from well 4 the vortex may jump to wells 3, 2, or 1, while from well 3 it may jump to wells 2 or 1.

Figure 4
figure 4

Vortex hopping between wells.

(a), Vortex trajectories in wells 1 to 6 (solid symbols) and hopping events between the wells shown schematically by dashed lines with a color matching the original well. The hopping between the wells results in hysteretic closed-loop trajectories that vary upon repeated cycles of the full loop and of the sub-loops. (b), The restoring force of the wells Fdc = −Fr(x) with the hopping events (dashed lines with a color matching the original well). The vortex jumps to the right (left) when a positive (negative) applied force exceeds the restoring force. The vortex stops at a position where the restoring force of the new well equals the applied force (dashed lines are horizontal). Well 6 exists only at positive forces and well 3 only at negative forces. The jumps to the right from well 3 to well 4 occur against the direction of the driving force when the value of the applied force drops below the minimum restoring force of well 3. (c), 2D potential due to a random distribution of defects, marked by ×, of equal U0 = 0.66 eV and average density of 200 µm−2. The stationary trajectories upon tilting the potential are shown by the solid lines and the dynamic escape trajectories by dashed lines with colors matching the source well. (e–j), Selected Bac(x,y) images from a movie (S6) of the ac vortex response to Fac = 93.1 fN ptp in different wells at the indicated values of Fdc. The gray scale spans 20 µT in all images.

Full size image

The above results clearly indicate that the observed vortex dynamics cannot be described by a sparse distribution of large pinning centers that are well separated from each other. In addition, SEM and AFM inspection of the same region of the sample (see Figs. S2 and S3) do not reveal any significant morphological defects at the locations of the potential wells. The observed pinning behavior, however, can be ascribed to arrays of closely spaced smaller materials defects as following. Our detailed numerical investigation of random disorder shows that the vortex response changes drastically if the potential wells of individual defects overlap. For instance, two small defects separated by a distance form two distinct potential wells separated by a barrier (Figure S10a). However, at smaller separations, , an interesting situation occurs in which the two defects form a single potential well, but U(x) develops an intrinsic softening and an inflection point in the restoring force leading to a peak in xac in the center of the well, as shown in Figures. S9a–c. For two identical defects, the softening occurs exactly in the center of the well where the attractive forces of the two defects balance each other, leading to a U-shaped potential well. This symmetric configuration is readily perturbed if the defects have different U0 or if other defects are nearby.

By analyzing a cluster of four defects, we can reproduce the results of our SOT vortex microscopy with startling agreement between the experimental and numerical results shown in Figure 2i–l: 1) The vortex displacement has a sharp spring softening peak in the middle of the well (Figure 2i) and a corresponding inflection point in the restoring force (Figure 2k). 2) The potential structure is substantially wider than ξ. 3) There is a significant anisotropy of the vortex response (Figure 2j) and asymmetry between positive and negative drives (Figure 2l). This anisotropic vortex response occurs here in a cluster of isotropic pinning defects, unlike the anisotropic depinning in a network of planar defects such as grain boundaries in polycrystals35. 4) The trajectory has an S shape with an inflection point (arrow in Figure 2j) that clearly matches the location of the inflection point in the restoring force (arrow in Figure 2k), as we indeed observe experimentally.

The analysis of this multi-defect cluster also provides an important insight into the observed broken-spring effect. At zero driving force, the four close defects form a single potential well with its minimum at the origin. The blue solid line in Figure 5b shows the resulting potential U(x) along the line y = 0, parallel to the driving force. The corresponding restoring force ∂U/∂x (blue line in Figure 5c), is smooth and flattens out at its maximum and minimum values, similar to that of a single defect (Figure 2c). However, as the potential is tilted by the driving force, the vortex moves along an intricate 2D trajectory shown in Figure 5a. In particular, for a small positive Fdc, only one potential minimum (magenta dot in Figure 5e) and one saddle point (black dot) are present. At Fdc = 1.04 pN, however, a new metastable well appears with a new minimum and saddle point (light green and yellow dots in Figures 5f and 5g). This additional well produces a sharp ripple in the projection of the potential U(x) and of the corresponding restoring force, onto the direction of the driving force (Figures 5b and 5c). Thus, in contrast to the common perception that the pinning potential of multiple defects is smooth on the scale of ξ, a multi-defect potential along the projection of the intricate vortex trajectory onto the direction of the Lorentz force can have sharp ripples on length scales substantially shorter than ξ. Because of these ripples, the restoring force terminates quite abruptly as Fdc approaches a narrow region near the end points of the magenta line in Figure. 5c, giving rise to the broken-spring response. Interestingly, Figures 5a and 5c show that, upon exiting the central (magenta) well to the right, the vortex hops into the green metastable well, while, upon exiting to the left, the vortex escapes without passing through the red metastable well. Thus, the effects of the ripples persist even if the vortex does not actually hop into the metastable wells.

Figure 5
figure 5

Simulation of vortex potential and dynamics in a multi-defect well.

(a), Calculated 2D vortex potential at zero driving force due to a cluster of four point-defects at locations marked by × (defects A, B, C and D contribute a Lorentzian potential with U0 of 1.41, 1.41, 2.0 and 2.0 eV respectively). Overlayed is the calculated trajectory of the vortex upon varying the driving force Fdc: solid color lines – loci of static potential minima points; dashed lines – loci of inflection points; white solid lines – dynamic vortex escape paths out of the central well at positive and negative critical forces. An expanded view of the static trajectory in the central well is shown in Fig. 2j. (b), U(x) along the stationary vortex trajectory in (a) (color solid and dashed segments) as compared to U(x) along the y = 0 line in (a) (solid blue). (c), The corresponding restoring force Fdc = −Fr = ∂U/∂x. The dashed lines (saddle points in (a)) are unstable solutions. The dotted lines show the escape of the vortex at the critical forces out of the central well. (d), Black: activation barrier between the central minimum (magenta in (a)) and the main saddle point (dashed black in (a)) vs. Fdc. Yellow: activation barrier between the central minimum and the metastable saddle point (dashed yellow in (a)) that is formed at Fdc>1.04 pN. The central minimum disappears for Fdc>3.1 pN. The dashed line marks ΔU = 34kBT = 12 meV, at which thermal activation becomes relevant. (e), 2D vortex potential at Fdc = 0.82 pN at which one minimum (magenta) and one saddle point (black) are present. (f), 2D potential at Fdc = 1.15 pN at which two minima (magenta and light green) and two saddle points (yellow and black) are present. (g), Same as (f) at Fdc = 2.70 pN. For Fdc>3.1 pN, only the light green metastable minimum remains. (h), 2D potential at Fdc = −4.52 pN, at which only the central minimum (magenta) and a nearby saddle point (brown) are present.

Full size image

Broken-spring behavior is usually associated with the so-called pin-breaking mechanism that results from bending distortions of a long vortex trapped by a strong pinning center37,38,39,40. In our case, however, bending distortions of the vortex are suppressed because the thickness of our film is smaller than the diameter of the non-superconducting core, 23/2ξ = 131 nm. A pinhole of radius a>ξ with sharp boundaries can also result in a hysteretic pinning potential U(x,y) with no reversible quadratic part at small displacements41, which is inconsistent with our SOT data shown in Figure 2. Our numerical simulations of the Ginzburg-Landau equations (see S13) for the case of strong pinning (due to Tc(r) depression in a region of radius a~ξ and smooth recovery over the length ~ξ at r > a) gave a potential well U(r) similar to that shown in Figure 2d, including the softening of the spring constant at the inflection point (Figure S11). The simplifying assumption of a vortex in a rigid potential of multiple pinning wells therefore does not change the main conclusions of this work. As a result, our model of potential ripples in a 2D random potential formed by an array of overlapping single wells U(r) is applicable to both weak and strong pinning and it presents a new mechanism for spring-breaking that describes our experimental data surprisingly well.

Another ingredient of the spring-breaking is thermal activation, which is usually disregarded for conventional superconductors at low temperatures11,42. Figure 5d shows that the typical energy barrier for thermally-activated hopping of vortices between the potential minimum and the main saddle point (black curve) is large () and decreases smoothly with Fdc. As a result, thermal activation at 4.2 K becomes relevant only within a few percent of the critical force Fc, at which (see S9 for details). For a single defect, the spring constant at Fc−Fdc~10−2Fc is reduced significantly, resulting in xac that is about five times larger than at the bottom of the well (Figures 2a and S10b) and inconsistent with the experimental data (Figure 2e). However, the metastable wells due to potential ripples create multiple saddle points separated by much smaller activation barriers (yellow line in Fig. 5d) that can cause premature thermal activation of the vortex, facilitating the broken-spring effect (as shown in Figures 2k and 2i). At J~Jc, the heights of these metastable barriers depend weakly on Fdc, resulting in thermally-activated hopping of vortices over a wide range of applied currents, consistent with our experimental data. Hopping of vortices over these small potential ripples may also be relevant to the outstanding problem of nearly temperature-independent relaxation rates s(T, H) = dln(J)/dln(t) of magnetization currents in the critical state of conventional superconductors, for which s(T) remains nearly constant even at 40,42.

Based on the above insights, we performed a full analysis of a 2D potential comprising a random distribution of defects. Figure 4c shows the potential landscape and the resulting static vortex trajectories inside the wells, as well as the dynamic escape trajectories between the wells (dotted lines). The main features—including the extent of the wells, shape of the trajectories, metastable wells, typical hopping distances and the transverse displacement between the wells—are in good qualitative agreement with the experimental results. In addition, the wells show the broken-spring effect and inflection points in the restoring force (Figure 4d) coinciding with the inflection points in the static trajectories. Consistent with our SOT observations, the vortex trajectories in Figure 4 form closed loops that provide the means for controlled manipulation and braiding of vortices for topological quantum computation43.

In conclusion, the new scanning SQUID-on-tip microscopy enabled us, for the first time, to measure the fundamental dependence of the elementary pinning forces on vortex displacement. The totality of our experimental and computational results shows that a vortex typically interacts with small clusters of a few pinning defects separated by about the coherence length. At low currents, the random multi-scale pinning landscape results in complex vortex trajectories and unusual softening within the potential wells. On approaching the critical current, the 2D random configuration causes fragmentation of the potential into metastable wells and gives rise to sharp ripples in the restoring force, triggering abrupt thermally-activated depinning of vortices even in the case of strong pinning and low temperatures, for which no significant thermal relaxation is expected. These results provide new insights into the pinning of vortex matter, mechanisms of magnetic relaxation in superconductors at low temperatures, the nonlinear response of superconductors to strong alternating electromagnetic fields and the development of high-critical-current conductors with artificial pinning nanostructures. This work may also open exciting opportunities in the controllable manipulation of single vortices on nanometer scales, particularly in quantum computations based on braiding and entanglement of vortices in thin film nanostructures.

Methods

The SOT that was used for scanning in this work was a Pb-based device33 with an effective diameter of 177 nm, 103 µA critical current at zero field and white flux noise down to 230 nΦ0Hz−0.5 (S1). The SOT was integrated into a scanning probe microscope with a scanning range of 30×30 µm2 44 and read out using a series SQUID array amplifier45. All measurements were performed at 4.2 K in He exchange gas at a pressure of 0.95 bar.

A 75 nm thick Pb film was deposited by thermal evaporation and capped by 7 nm of Ge. The film was patterned lithographically into an 8 µm wide microbridge fitted with electrical contacts to allow the application of transport currents (S2).

A square wave ac current Iac of 0.56 mA peak-to-peak (ptp) and frequency of 13.3 kHz was applied to the sample, resulting in a Lorentz force Fac = Φ0Jac = 93.1 fN ptp on the vortex, where Jac is the corresponding sheet current density at the location of the vortex in the center of the microbridge in the Meissner state46. In the softening peak regions, the ac current and the driving force were reduced by a factor of ten, to Fac = 9.31 fN, in order to keep xac below 1 nm. The ac current was superimposed on a dc current Idc in the range of ±27 mA (applying a dc Lorentz force in the range of Fdc = ±4.44 pN). The size of step in Idc was kept equivalent to the ptp value of Iac in order to facilitate the displacement integration procedures. At each value of Fdc, full images of Bdc and Bac were acquired simultaneously, with the SOT scanned at a constant height of about 150 nm above the sample. The frame size was typically 2.2×1.3 µm2 with pixel size of 10 nm scanned at a speed of 2 µm/sec, taking about five minutes to complete.