Introduction

Metal nanostructures and composite nanomaterials play a significant role in linear and nonlinear optics. The optical responses of metal nanoparticles arise from the collective oscillations of their conduction electrons and the characteristics of the resulting localized surface plasmon resonances strongly depend on several parameters, such as the nanoparticle shape1,2,3,4, size5,6,7, orientation and dielectric environment. In the past decade, significant progress in various fabrication techniques has allowed to explore a large variety of shapes and structures, as well as the effect of the mutual arrangement of the particles. This has led to remarkable improvements in controlling the optical properties of nanostructures, allowing their responses to be tailored for specific applications ranging from imaging8,9 and biosensing10,11 to solar cells12,13.

The efforts on optical nanomaterials have followed two distinct lines. The first focuses on optimizing and understanding the enhanced optical responses of individual particles through particle shape (traditional spherical particles or ellipsoidal nanorice) or composition (solid vs. core-shell structures)2. The second line assembles collections of individual particles into nanocomposites with effective properties (metamaterials) enhanced compared to the constituent materials. The first effective-medium model for such composite materials was introduced more than a century ago by Maxwell-Garnett14.

The effective medium approach is particularly important from the viewpoint of new types of nonlinear materials, where the macroscopic properties of the sample can play a crucial role in determining whether a significant response can be obtained or not. The model of Maxwell-Garnett has been extended to include nonlinear effects and it has been shown that the third-order nonlinear susceptibility of a metal-dielectric bulk-type composite material can exceed that of either of its constituents and possess tensorial nonlinear properties very different from those of the host material15,16,17.

The requirements for second-order materials are even more demanding, because second-order effects, such as second-harmonic generation, are only possible in noncentrosymmetric media. The observation of second-order effects in metals has thus been mainly limited to surface geometries where symmetry is broken at the metal-dielectric interfaces. For example, it is well-known that SHG can be enhanced by rough metal surfaces18. More recently, SHG has been demonstrated in lithographic arrays of non-centrosymmetric particles19,20,21,22. In our previous work, we have shown that bulk-type multilayer composites made of alternating layers of silver-decorated silica glass nanoparticles and fused silica intrinsically give rise to symmetry-breaking at each interface between the pure silica glass and layers of decorated particles, resulting in a spontaneous growth of an overall non-centrosymmetric structure23. However, these results based on a single SHG signal do not provide information on how well the order of the structure is maintained as its thickness is increased.

In this paper, we present a detailed experimental investigation of the second-order response for such a bulk-type second-order nanocomposite material. We determine the second-order susceptibility tensors of the samples of different thickness. By comparing the relative values of the various tensor components, we show that the structural properties of the samples are well maintained as the sample thickness is increased. The samples are shown to have the expected isotropy in the sample plane and the independent components of the effective bulk susceptibility are found to be , , (where z is the direction of the layer normal). Our results provide a convenient reference for further optimisation of these types of structures, which can be fabricated using very straightforward techniques.

Sample Fabrication and Measurements

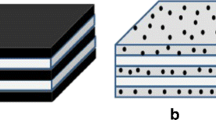
The nanocomposite samples consist of alternating layers of silver-decorated silica glass nanoparticles and pure silica glass deposited on top of a 1 mm thick silica glass substrate (microscope glass slide). The layers are prepared using a combination of aerosol and dielectric coating techniques as described in detail in23. Samples with different numbers of layers were prepared with an effective area of about 3 cm2. A schematic illustration of the nanocomposites together with an electron microscope image are shown in Fig. 1. The thickness of the layer consisting of metal nanoparticles is hn = 800 nm and the deposited layer of silica glass has a thickness of hS = 200 nm.

Figure 1
figure 1

(a) Schematic illustration of the nanocomposite samples. D is the thickness of the glass substrate, N is the number of layers and hn and hS represent the thickness of silver-decorated nanoparticles and pure silica glass, respectively. The SHG sources with the effective contribution from a single layer are indicated. (b) Transmission electron microscope image of the nanocomposite structure.

Full size image

Our previous results showed that the characteristics of the linear optical response of this type of nanocomposite are preserved during the multilayer growth and, in particular, the width and spectral position of the plasmon resonance remain independent of the amount of silver decorated particles and number of layers23. The measurement of the second-order nonlinear response further revealed that the intensity of the SHG signal grows with the number of layers with approximately the expected dependence23.

To fully characterize the second-order nonlinear response of the composite samples, we perform SHG measurements using a neodynium YAG laser (1064 nm wavelength, 72 ps pulse length, 34 µJ pulse energy). Polarization dependent measurements allow us to verify the symmetry group of the samples. Subsequent Maker-fringe measurements allows us to verify, that the SHG signal grows with the sample thickness as expected. Finally, by comparing both sets of measurements, we verify that all results can be described by a unique set of tensor components.

First we make the measurements for different combinations of the fundamental and SHG polarizations. The polarization of the fundamental laser beam is modulated with a half-wave plate (HWP) and the intensities of the p- and s-polarized SHG signals are recorded as a function of the HWP rotation angle. The results show that the s-polarized SHG signal vanishes for both p- and s-polarized fundamental beams implying in full agreement with the expected in-plane isotropy (C∞ν symmetry group) of the sample and electric-dipole origin of the effective response. The non-vanishing second-order susceptibility tensor components are then limited to χxxz = χzxz = χyyz = χyzy, χzxx = χzyy and χzzz, where z is the normal to the surface of the sample and x and y represent orthogonal in-plane directions.

Next, we perform Maker-fringe charaterization24,25 for four different samples with increasing number of nanoparticle-silica glass layers (1, 2, 3 and 4 layer samples) in the pin-pout polarization configuration. Measurements are also conducted for the glass substrate which is then used as the reference. A series of ten distinct measurements at different spatial positions on the sample surface is conducted to eliminate any effects from possible inhomogeneity and the results are averaged over all ten measurements. The results for samples of different thickness are fitted to a unique set of tensor components and their compatibility with the polarization measurements is finally confirmed.

Modelling

In general, the p- and s-polarized SHG field components generated in an achiral thin film with in-plane isotropy can be expressed as and Es = hepes26, where ep and es represent the p- and s-polarized components of the fundamental beam, respectively and f, g and h are expansion coefficients that depend linearly on the susceptibility tensor components, angle of incidence and linear optical properties of the material. Within the framework of a simplified Green's function formalism27,28, where the multiple reflections within the thin nanocomposite layers and absorption are neglected, these expansion coefficients take the form

where , and are the phase factors arising from the propagation of the fundamental and second-harmonic fields inside of the structure with the total number of layers N and are expressed with the sums:

The subscripts 1, 2 and 3 refer to air, silica glass and nanocomposite layers, respectively (see marked areas on the schematic image in Fig. 1(a)) and is the reduced frequency (c is the speed of light in vacuum), hS denotes the thickness of the silica layer and hn the thickness of the nanocomposite active layers. In Eqs. 1–3, we have used lowercase and uppercase notation to define quantities at the fundamental and SHG frequencies, respectively. With this notation ni (Ni) is the refractive index of the ith region at the fundamental (SH) frequency and θi (Θi) the angle of propagation of the fundamental (SH) radiation with respect to the structure normal inside the ith region. Also: . The coefficients tpij and tsij (Tpij and Tsij) account for the partial transmission of the s- and p- fundamental (SHG) field components at the interface between regions i and j, respectively and they can be calculated from28

The refractive indices of the silver-decorated nanoparticle layers were calculated using an effective medium approach16. Taking into account the high porosity of the nanocomposite, we estimated nAg/glass and NAg/glass to be 1.102 and 1.122 at the fundamental and SH wavelengths, respectively29. Equations 1–8 can then be used to validate the results of the fitting of the three independent tensor components , and of a single active layer (decorated particles + silica glass) of the nanocomposite for the performed Maker-fringe fittings.

In order to evaluate the absolute values of the active layer tensor components and separate the contribution from the glass substrate, we calculate the SHG fields generated from each interface and the resulting total SHG amplitude. Because the different layers of the samples were prepared under identical conditions, we assume that each interface is an identical source of nonlinear radiation and contributes equally to the total SHG signal such that the total SHG amplitude simply corresponds to the sum of the interfering SHG fields generated at each interface. The SH intensity generated from the multilayer structure is then given by

The SH fields E1 and E2 represent the contributions from the air-silica interface in region 1 and silica-air interface in region 2, respectively and E3 corresponds to the total contribution from the nanocomposite layers. For p-polarized fundamental and SHG light, as used in the Maker-fringe measurements, they can be expressed as27,28

and

Here, the constants , and 30 represent the independent tensor components of the second-order surface response of the air-silica interface which are defined in terms of the fields inside the material. , on the other hand, is a constant, where ep is the amplitude of the incident p-polarized beam and hn, hS and D denote the thickness of the silver-decorated nanoparticle layer, fused silica layer and glass substrate, respectively.

The total contribution E3 of the nanocomposite multilayers (region 3 in Fig. 1) to the SH field consists of multiple silica-nanoparticles interfaces which depends on the number of deposited layers N as

where the contribution of the kth layer to the total SHG signal is:

We are now in the position to determine the absolute values of the tensor components of a single active layer of the nanocomposite by fitting Eqs. 9–13 to the Maker-fringe patterns and Eqs. 1–8 to the HWP polarizaration measurements.

Results

The results of the HWP measurements for different input/output polarization combinations at a 62° angle of incidence corresponding to maximum SHG signal are shown as squares and triangles in Fig. 2. They allow us to determine that the investigated samples posses in-plane isotropy, which limits the surface tensor components to the three independent elements as discussed above. The measurement for the 4-layer sample is presented in Fig. 2. The Maker-fringe measurement of a clean glass substrate alone (i.e. for the case of N = 0 in the model described with Eqs. 9–13) is illustrated in Fig. 3. The total SH intensity reduces to contributions from the air-glass and glass-air interfaces only (see Eqs. 10 and 11) and we see very good agreement between the theoretical model and the experimentally measured data for refractive indices nglass = 1.45 and Nglass = 1.46 at the fundamental and SHG wavelengths, respectively29. The thickness of the substrate was estimated to be D = 1061.2 µm in order to match the period of the Maker fringes between the theory and measurement. The Maker-fringe measurements for the nanocomposite are plotted in Fig. 4 as black solid lines and show a clear increase in the SH signal for a growing number of layers with a maximum signal at around 62° incidence. In order to fit these data with the model described by Eqs. 9–13, we first make coarse estimates of the thicknesses for all the samples, to match the fringe pattern with the experimental one. Next, we set the absolute values of the tensor components as free running parameters and perform a robust fit using the least-square method. In the fitting procedure we account for all data points measured for all samples at the same time.

Figure 2
figure 2

Experimentally measured intensity at 532 nm for p- (black triangles) and s-polarized (red squares) SHG as a function of the HWP rotation angle modulating the polarization of the incident beam at 1064 nm.

The angle of incidence was fixed to 62°. The results are normalized with respect to the p-polarized SHG intensity. Solid lines show the theoretical fits from Eqs. 1–8. The black arrows indicate the polarization of the incident fundamental field.

Full size image
Figure 3
figure 3

Comparison between the theoretical model of Eqs. 9–11 (red solid line) and experimentally measured SHG intensity (black solid line) vs. angle of incidence for the glass substrate.

Full size image
Figure 4
figure 4

Maker-fringe measurements (black solid line) with fitted model (red solid line).

The averaged thicknesses of the silica glass and nanoparticles layers estimated from the microscope image (see Fig. 1(b)) are hS = 200 nm and hn = 800 nm, respectively. Number of layers: a) 1 layer sample, b) 2 layers sample, c) 3 layers sample, d) 4 layers sample.

Full size image

The results of the fits shown in Fig. 4 as red solid lines are in excellent agreement with the measured data for all the samples with different number of layers. In particular, the overall increase in the SH intensity as a function of the number of layers is correctly reproduced, as well as the modulation depth and period of the fringes. The corresponding absolute values of the nonlinear tensor components of the nanoparticle-silica interface obtained from the fit are summarized in Table I.

Table 1 Calculated absolute values for the surface tensor components of a single nanocomposite layer, as well as the effective bulk response obtained from these values
Full size table

The values of the tensor components of the nanoparticle-silica interface , and are finally validated by the polarization measurements. Using Eqs. 1–3, we are now able to calculate the complex parameters f, g and h. The calculated parameters are next used to draw the expected line shape for the HWP measurements. The fit is presented in Fig. 2 as solid lines. The results of the measurements are normalized with respect to the p-polarized data, as well as the calculated line shape. The measured data points and determined line are in excellent agreement, therefore validating the values of the tensor components.

Discussion

The dominant component of the nanocomposite layer interface is χzzz, however its value is lower than the same component of the glass surface. Note also, that the components χzxx and χxxz are also relatively large and unequal. These results allow us to make some conclusion about the character and possible origin of the nonlinear response of the nanocomposite. The components χzxx and χxxz must be equal when Kleinman symmetry is valid (i.e., far from any material resonances) or when the macroscopic nonlinearity arises from the orientational average of microscopic constituents whose nonlinearity is dominated by a single diagonal component of the hyperpolarizability tensor (which is the case for, e. g., rod-like push-pull molecules31). In the present case, our SHG wavelength is already at the wing of the plasmonic extinction band of the silver particles, whose presence is essential for the nonlinear response. The Kleinman symmetry is therefore not operative. In addition, if the silver nanoparticles are considered as the microscopic consitituents, their nonlinear response cannot be reduced to a single tensor component. Instead, more components need to be considered even on the microscopic level, which will significantly complicate analyzing the connection between the microscopic and macroscopic responses. In addition, the fact that one of the off-diagonal components χxxz is almost as large as the diagonal component χzzz suggests that the orientational distribution of the microscopic constituents is relatively broad. This agrees well with the fact that the silver particles are randomly distributed on the surface of the silica particles. Hence, the properties of the silver particles are only modified by the porosity of the silica glass layer that leads to a varying dielectric environment around the silver particles at different vertical positions of a given silica particle. This suggests that the tensorial properties of the macroscopic nonlinearity could be tuned by controlling the porosity of the structure. Nevertheless, it is fair to say that it will be a significant challenge to build a detailed model that connects the microscopic origin of the nonlinearity to the macroscopic response.

We also note that the values of the bulk nonlinearity reported in Table I are relatively weak. This arises from the fact that the effective bulk response has been obtained by dividing the measured effective surface response by the layer thickness. For the present samples, the layer thickness is unnecessarily large and could easily be reduced by at least one order of magnitude, resulting in a more respectable bulk-type response. Further enhancement is expected from the optimization of the size and surface coverage of the silver decorated nanoparticles.

Conclusions

In conclusion, we have performed a detailed characterization of the second-order nonlinear response of multilayer silver nanoparticle-silica nanocomposites. Using a simplified Green's function formalism, which allows to describe mathematically the sources at the interfaces between the two materials and fitting the Maker-fringe patterns of the multiple samples, we have determined all the independent tensor components of the nanocomposite samples. The fact that samples of different thickness can be described by a single set of nonlinear parameters shows that the level of ordering of the samples can be maintained for increasing sample thickness. The relative values of the tensor components allowed us to make some conclusions about the mechanism underlying the nonlinear response. The effective bulk nonlinearity of the investigated samples is relatively low but can likely be increased by reducing the sample thickness. It will also be interesting to investigate how much the nonlinear response can be boosted by increasing the amount of metal in the structure and by operating closer to the plasmon resonance. In any case, the present results provide a well-defined baseline for further optimization of these types of nanocomposite materials for second-order nonlinear effects.