Introduction

Ask a fluid mechanician the following question: If a bubble of density ρ1 rises in a fluid of density ρ2, would a drop of density ρ2 rise in fluid of density ρ1 in the same way, if gravity were reversed? The answer is likely to be a yes (except from experts on the topic), with a caveat that viscosity must be appropriately reassigned. The correct answer is a no1 and in this paper we study the physics behind this difference. We show how vorticity tends to be concentrated in the lighter fluid and this changes the shape and the entire behavior. By the term bubble we mean a blob of fluid which is lighter than its surroundings and by drop a fluid blob that is heavier than its surroundings. We discuss the limit in which a drop and bubble can behave the same and present two alternatives in this limit to design an equivalent drop for a bubble.

Due to their importance in industry and in natural phenomena and due to their appeal to our scientific curiosity, bubbles and drops have been studied for a long time. The literature on this subject is therefore huge, with several review articles by several authors2,3,4 and others. Appealing introductions to the complexity associated with bubble and drop phenomena can also be found in Refs. 5, 6. There are yet many unsolved problems, which are the subject of recent research (see e.g.7,8,9,10,11,12,13). Bubbles and drops have often been studied separately, e.g.11,14,15,16,17,18 on bubbles and19,20,21,22,23,24 on drops. However, there is also a considerable amount of literature which discusses both together, e.g.25,26,27,28,29,30.

When the bubble or drop is tiny, it merely assumes a spherical shape, attains a terminal velocity and moves up or down. An empirical formula for the terminal velocity of small air bubbles was found by Allen31 in 1900. Later, two independent studies by Hadamard25 and Rybczynski32 led to the first solution for the terminal velocity and pressure inside and outside of a slowly moving fluid sphere in another fluid of different density and viscosity. The spherical vortex solution due to Hill33 has been a keystone for most of the analytical studies on the subject. Later studies1 showed that at low Reynolds and Weber numbers, drops and bubbles of same size behave practically the same way as each other, both displaying an oblate ellipsoidal shape.

Bigger drops and bubbles are different. A comparison of bubble and drop literature will reveal that in the typical scenario, bubbles dimple in the centre14,34 while drops more often attain a cup-like shape13,35. This difference means that drops and bubbles which break up would do so differently. The dimples of breaking bubbles run deep and pinch off at the centre to create a doughnut shaped bubble, which will then further break-up, while drops will more often pinch at their extremities. A general tendency of a drop is to flatten into a thin film which is unlike a bubble. There could be several other modes of breakup (see35) like shear and bag breakup for drops falling under gravity and catastrophic breakup at high speeds.

We mention a few significant numerical studies before we move on. Han & Tryggvason35 studied the secondary break-up of drops for low density ratios, whereas Tomar et al.56 investigated the atomization involving the break-up of liquid jet into droplets. We also note that recent developments in the field of lattice Boltzmann simulations54,55 allow one to simulate multiphase flows with high density ratio by using a clever doubly-attractive pseudo-potential.

We now pose the problem and discuss our approach to its solution.

Problem formulation and approach

The geometry and equations

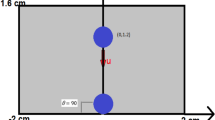
The drop or bubble is initially spherical with radius R and has viscosity and density µi and ρi respectively, which are different from the respective quantities µo and ρo for the surrounding fluid. The fluids are assumed to be immiscible, incompressible and Newtonian. Figure 1 is a schematic diagram of the initial configuration, where x and z represent the horizontal (radial) and vertical (axial) directions, respectively. The subscripts ‘i’ and ‘o’ stand for inner and outer fluid, respectively, σ is the surface tension coefficient between the two fluids and g the acceleration due to gravity. We study an axisymmetric flow, with the velocity and pressure fields denoted by u(u, w) and p respectively, wherein u and w are the velocity components in the x and z directions, respectively. We treat the flow as isothermal.

Figure 1
figure 1

Schematic diagram showing the flow domain as a box surrounding a bubble/drop and the axis of symmetry as a dot-dashed line.

The outer and inner fluid phases are designated as ‘o’ and ‘i’, respectively.

Full size image

Given the physical quantities in the problem, the Buckingham-pi theorem requires four independent dimensionless parameters to completely describe the system and the ones we choose are the density ratio r, the viscosity ratio m, the Galilei number Ga and the Bond number Bo. These are defined respectively as r ≡ ρi/ρo, m ≡ µi/µo, Ga ≡ ρog1/2R3/2/µo and Bo ≡ ρogR2/σ. The governing equations are thus non-dimensionalised using R, , µo and ρo as length, velocity, viscosity and density scales, respectively. Note that the Galilei number is like a Reynolds number, but defined by the gravity velocity scale rather than the actual forward velocity of the bubble. Since the latter is unknown a priori and depends on several physical quantities, the present velocity scale is a cleaner one to adopt and we do so in our study. For our discussions however it will be useful also to define a Reynolds number Re ≡ ρoU0R/µo and a Weber number and , where U0 is a typical bubble velocity. Note that each of the four dimensionless parameters, when independently varied can change the dynamics of the blob. Along with the continuity equation:

the momentum equation can be written with a continuum model for surface tension forcing (see36) as

wherein is the unit vector in the vertically upward direction; δ is the Dirac-delta function, a location on the interface and n its unit normal and is the material derivative. On the right hand side, we have the pressure, viscous, gravitational and surface tension forces per unit volume respectively. Note that ρ and µ are now dimensionless quantities, respectively scaled by the density and viscosity of the outer fluid.

Thus the surrounding or outer fluid obeys

whereas the inner fluid, namely the drop or bubble, satisfies

with the interfacial conditions at x = xs being continuity in velocity and the relevant stress balance. The surface tension term appears in the normal stress balance, which is pi|s = po|s + k/Bo wherein k is the local surface curvature defined as .

Numerical simulations

In the framework of the diffuse-interface method37, we express the surface tension term in the momentum equation (2) in the form

and solve it along with the Cahn-Hilliard equation

and the continuity equation (1). Here c is the volume fraction of the outer fluid, M = c(1 − c) is the mobility, is the chemical potential wherein is a measure of interface thickness, is the bulk energy density and α is a constant; Pe ≡ RV/(Mcϕc) represents the Péclet number wherein Mc and ϕc are fixed characteristic values of mobility and chemical potential, respectively (see37 and references therein for more details). The dimensionless density and viscosity of the fluids are taken to be linear in c, as

where the value of c is one and zero for outer and inner fluids, respectively.

Symmetry boundary conditions are applied at x = 0 and Neumann boundary conditions are used at the other boundaries. To avoid numerical effects from the outer boundaries on the flow a computational domain of width 16R and height 64R is found to be sufficient for most of the cases, consistent with the study of Uno & Kintner38. Where needed, larger domains have been used and it has been checked that the results are independent of the domain size. In addition, the open source code Gerris, created by Stéphaen Popinet39 has been used for simulating drops which become very thin as compared to their initial radius. The adaptive grid refinement feature in Gerris was exploited for our benefit which saved a lot of time in our numerical study. The numerical method used and its validation are discussed in detail in the supplementary material. This code has previously been used extensively to study various miscible and immiscible flows (see e.g. Mishra et al.40). The supplementary material contains more information about the numerical methods and comparisons with analytical results in the creeping and potential flow limits.

Drops versus bubbles: when must we discriminate?

Let us first consider a solid spherical object falling through the fluid. Its equation of motion in Stokes flow (small Ga), rendered dimensionless with the same scales as before, is

where H is the vertical location of the centre of the sphere and a dot represents a time derivative. Maintaining Ga the same, it is easy to see that with gravity inverted and setting

a light solid bubble would attain the same steady state velocity. The subscripts d and b have been added to distinguish drop from bubble. Equation (8) makes it obvious however that in the transient phase, the accelerations of the bubble and drop must be different, which means that at steady state, the vertical locations of the drop and bubble will have a constant displacement. Note also that for every rb < 1, we can find a realistic rd. However for rd > 2, there is no equivalent positive rb. In other words, every solid bubble has an equivalent solid drop, but drops heavier than rd = 2 do not have an equivalent bubble.

The next question is, does the same relationship carry across to fluid bubbles and drops. The fact that the gradients in the viscous stresses and pressure inside the drop do not disappear any more makes the problem more complicated but, guided by Taylor and Acrivos1 we may look for an equivalence in the limit Re ≪ 1 and We ≪ 1, i.e., when we will have small inertia and a near-spherical drop. Hadamard's formula25 for drag will apply in this case and the equation of motion now is

For a small or slowly moving drop, the O(Ga) terms can be neglected. For a Hadamard flow

and it is seen that this expression reduces to the factor 9/2 in equation (8) in the limit of infinite inner-fluid viscosity. Equation (10) is a first-order ordinary differential equation in , which can be integrated analytically. Given that the drop starts from rest, its velocity is

and equivalently for a bubble with gravity reversed,

For the terminal velocities of the two to be the same, we must have

For the outer fluid to have the same dynamics in drop and bubble cases, we must have, from equation (3),

while for the pressure jump across the interface to be the same in the two cases we need

In addition, we would like the two to have the same history, i.e., to have been at the same position at the same time. This requirement is met for a Hadamard flow by setting

where we have made use of the expression (11). Using equation (17), equation (14) yields

Keeping the Galilei numbers the same, condition (17) will yield positive values of md for a given mb only when rd is less than a certain quantity. For the range 0.01 < mb < 100, we find rd must be less than ~1.2 and therefore rb >~ 0.86. Thus the equivalence applies only in a small range of density ratios. In other words, at low Ga and Bo, a drop falling through a surrounding fluid of slightly lower density will display dynamics closely matching that of a corresponding bubble rising through slightly denser fluid. The dimensionless parameters of the drop and bubble are related by equations (15) to (18). On the other hand, as seen from equation (18), when r is significantly different from 1 the dynamics of a drop should be qualitatively different from any bubble.

We now examine whether any equivalence is possible at higher Ga and Bo between a drop and bubble. The force balance, written in order of magnitude terms (in dimensional form) reads as

where tildes in the superscript represent dimensional quantities. It is clear that for the pressure field in the surrounding fluid in the bubble and drop case to be the same, the nonlinear term in the velocity must be small, i.e., the flow must be gravity and not inertia dominated, or the Froude number, V2/(gR) ≪ 1. In this case, the drag scales as the forward velocity of the drop, so we have V ~ ΔρgR2/µ and we have

Similarly, for surface tension to overwhelm inertial effects as far as the dynamics is concerned and thus not allow for significant shape change of the drop, we must have ρV2/R ≪ σ/R2, yielding

Thus an equivalence between a drop and bubble must be possible when r → 1, even if Ga and Bo are not small, so long as inequalities (20) and (21) are satisfied. In this limit, it is usual to apply the Boussinesq approximation, by which the fact that the densities of the drop and the surrounding fluid are different will only affect the gravitational force term in the Navier-Stokes equation. In other words, r is set to 1 everywhere except in the gravity term. For drops it was noted by Han & Tryggvason35 that the Boussinesq approximation gives reasonable results for 1 < r < 1.6. Interestingly, if we had begun by making the Boussinesq approximation, the Navier-Stokes equation would yield an equivalent bubble for a given drop with rb = 2 − rd and mb = md. We examine in the following section which of these choices will work better.

Results

Drop and bubble similarities and differences

In all cases where we compare drops and bubbles, the Galilei number and Bond number are kept the same for the bubble and the drop. In the case where inertia is small and surface tension is large, we saw that an equivalent bubble for every drop may be found when r is close to 1. We show in figure 2 the vertical location of the centre of gravity, nondimensionalised with the initial radius of the drop, of small inertia and high surface tension, with a density ratio r = 1.214 and viscosity ratio m = 76.0 as compared to its surroundings, obtained from numerical simulations. Also shown are the vertical locations of an equivalent bubble obtained from equations (17) and (18) and also one with rb = 2 − rd and mb = md. For ease of comparison, the direction of gravity is reversed for the drop in all the results presented. It is seen that the bubble obtained by equating the Hadamard drag produces a better equivalent bubble than one obtained by a priori making the Boussinesq approximation. All the blobs remain practically spherical till the end of the simulation shown.

Figure 2
figure 2

Vertical location of the center of gravity as a function of time for a drop (r = 1.214 and m = 76), an equivalent bubble based on Boussinesq approximation (r = 0.786 and m = 76) and an equivalent bubble based on conditions (17) and (18) (r = 0.85 and m = 0.1).

The rest of the parameters are Ga = 6 and Bo = 0.0005.

Full size image

At small inertia and moderate surface tension (not shown), bubbles and drops do not remain spherical, but with the density ratios close to 1 and density and viscosity ratios related by equations (18) and (17), a bubble and drop display the same shape and dynamics as a function of time. We now consider bubbles and drops of higher inertia, where the inequalities (20) and (21) are not obeyed. Drop shapes obtained numerically for a density ratio close to unity are shown for this case in figure 3(b). The Galilei and Bond numbers are the same for the bubble and the drop and the densities are related by equation (18). The Reynolds number based on the terminal velocity of the bubble and the drop is about 16. The kinematic viscosity ratio m/r for the bubble is kept the same as the drop in figure 3(a) and related by equation (17) in figure 3(c). It is apparent that a drop and its equivalent bubble behave qualitatively the same. The velocities of the drop and bubble are closer to each other when the viscosity relation (17) is used whereas the shapes are closer together when they have the same kinematic viscosity ratio.

Figure 3
figure 3

Evolution of (a) bubble shape with time for r = 0.9, m/r = 0.56. (b) drop shape with time for r = 1.125, m/r = 0.56. (c) drop shape with time for r = 1.125, with viscosity obtained from equation (17). The direction of gravity has been inverted for the drop in order to compare the respective shapes with those of the bubble. In all three simulations, Ga = 50, Bo = 50 and the initial shape was spherical.

Full size image

When the density ratio is far from unity, no equivalence is possible. Equation (17) is no longer valid, nor possible to satisfy. We therefore compare drops and bubbles of the same m/r. Figure 4 makes it evident that neither the shape nor the velocity of the drop and bubble are similar to each other.

Figure 4
figure 4

Evolution of (a) bubble and (b) drop shapes with time, when densities of outer and inner fluid are significantly different.

As before, for the drop (right column), the direction of gravity has been inverted. In both simulations Ga = 50 and Bo = 10. The other parameters for the bubble system are r = 0.5263 and m = 0.01, while for the drop system r = 10 and m = 0.19. Note the shear breakup of the drop at a later time. Shown in color is the residual vorticity (Kolar, 2004).

Full size image

Shown in color in this figure is the residual vorticity Ω41, which is a good measure of the rotation in a flow. It is just the vorticity from which the shear part has been subtracted in a manner slightly different from that in the Okubo-Weiss parameter and is discussed in greater detail in the supplementary material. Especially at later times in this figure, it is evident that residual vorticity is concentrated within the bubble but outside the drop. This is the primary difference between a bubble and a drop. The region of low pressure and high vorticity tends to lie in the lighter fluid. In the case of the bubble, this causes an azimuthally oriented circulation in the lower reaches, which then leads to a fatter base and aids in a pinch-off at the top of the bubble. In the case of a drop, the vorticity being outside means that the lower portion of the drop is stretched into a thin cylindrical sheet and an overall bag-like structure is more likely. Also a pinch off in this sheet region is indicated rather than a central pinch-off. We present in figures 5 and 6 streamlines at various stages of evolution in this simulation. Closed streamlines are visible in the region of lower density, indicative of regions of maximum vorticity being located in the lighter fluid.

Figure 5
figure 5

Streamlines in the vicinity of a bubble for t = 1, 2, 3 and 4 for parameter values Ga = 50, Bo = 10, r = 0.5263 and m = 0.01.

The shape of the bubble is plotted in red.

Full size image
Figure 6
figure 6

Streamlines in the vicinity of a drop for t = 1, 2, 3 and 4 for parameter values Ga = 50, Bo = 10, r = 10 and m = 0.19.

The shape of the bubble is plotted in red.

Full size image

The fact that regions of low pressure and high vorticity would concentrate in the less dense fluid follows directly from stability arguments. A region of vorticity involves a centrifugal force oriented radially outwards, i.e., pressure increases as one moves radially outwards from a vortex. There is a direct analogy (see e.g.42) between density stratification in the vicinity of a vortex and in a standard Rayleigh Bénard flow. In the latter, we have a stable stratification when density increases downwards. In the former, we have a stable stratification when density increases radially outwards, i.e., when the vortex is located in the less dense region.

Figure 7 is a demonstration that for the same outer fluid even if the viscosity of the bubble and the drop were kept the same and only the densities of the two were different, the behavior discussed above is still displayed.

Figure 7
figure 7

Evolution of (a) bubble and (b) drop (gravity reversed) shapes with time.

Parameters for both bubble and drop systems are: Ga = 100, Bo = 50 and m = 10. The density ratio for the bubble and drop are r = 0.52 and r = 13 respectively, based on equation (18).

Full size image

Our results thus indicate that density is the dominant factor rather than viscosity in determining the shapes of inertial drops and bubbles. In particular, the vorticity maximum tends to migrate to the region of lower density and this has a determining role in the shape of the structure. Since large density differences bring about this difference, these are effectively non-Boussinesq effects.

We note that given the large number of parameters in the problem, including initial conditions, which we have kept fixed, the location of maximum vorticity in the less dense region may not be universally observed in all bubble and drop dynamics. For example, the Widnall instability43 in drops resembles the central break-up we have discussed. In the usual set-up of the Widnall instability, the densities of the inner and outer fluid are close to each other, so we may expect the drop to behave similar to a bubble and the initial conditions are not stationary.

Our arguments above on vorticity migrating to the lighter fluid do not depend on gravity being present. We also confirm this in simulations which obtain the motion of a bubble and a drop started with a particular initial velocity in a zero-gravity environment. These are shown in the supplementary material.

Before breakup

Break-up of drops and bubbles is typically a three-dimensional phenomenon on which much has been said, see e.g. the experimental studies of44,45,46 theoretical work of47,48 and numerical study of13. The transient behavior of liquid drops has been discussed extensively49,50,51,52, especially in the context of internal combustion engines, emulsification, froth-formation and rain drops. However, the transient behavior of bubbles has not been commented upon as much and we make a few observations, regarding large-scale oscillations, that are not available in the literature to our knowledge. We note that since our simulations are restricted to axisymmetric break-up they may not always capture the correct break-up location or shape.

Various parameter ranges are covered in numerous papers in the past 100 years and it is known that drops and bubbles break up at higher Bond numbers. The Bond number below which a bubble of very low density and viscosity ratio does not break, but forms a stable spherical cap, is about 8 (see e.g.53) which is similar to that found in our simulations. We begin by associating a time scale ratio with the Bond number. It may be said that surface tension would act to keep the blob together whereas gravity, imparting an inertia to the blob, would act to set it asunder. The respective time-scales over which each would act may be written as for surface tension and for gravity. The ratio

is a measure of the relative dominance. At Bo ≫ 1, surface tension is ineffective in preventing break-up and we may expect a break-up at a time of O(1), since we use gravitational scales. For Bo ~ 1, it is reasonable to imagine a tug-of-war to be played out between surface tension and inertia in terms of shape oscillations, with a frequency of O(1). Since a bubble usually breaks up at the centre by creating a dimple, the vertical distance Dd of the top of the dimple from the top of the bubble is a useful measure to observe oscillations. Figure 8 shows the dimple distance as a function of time for various Bond numbers and our expectations are borne out.

Figure 8
figure 8

Variation of dimple distance versus time for Ga = 50, r = 7.4734 × 10−4, m = 8.5136 × 10−6.

Full size image

Figures 9 and 10 are typical streamline patterns in the vicinity of bubbles in the break-up and recovery cases respectively. Instantaneous streamlines are plotted by taking the velocity of the foremost point of the bubble as the reference, but the picture is qualitatively unchanged when the velocity of the centre of gravity of the drop is chosen instead. Both cases are characterized by a large azimuthal vortex developing within the bubble initially. In the break-up case (figure 9), this vortex is sufficient to cause the bubble surface to rupture and obtain a topological change, from a spherical-like bubble into a toroidal one. In all the cases of bubble recovery we have simulated, of which a typical one is shown (figure 10), there develop at later times several overlaying regions of closed streamlines, which act to counter the effect of rupture by the primary vortex and to bring back the drop to a shape that is thicker at the centre. During each oscillation, we see the upper and lower vortices form and disappear cyclically.

Figure 9
figure 9

Streamlines in and around the bubble at time, t = 1, 1.5, 2.0 and 2.5 respectively, for Ga = 50, Bo = 29, r = 7.4734 × 10−4 and m = 8.5136 × 10−6.

The shape of the bubble is plotted in red.

Full size image
Figure 10
figure 10

Streamlines in and around the bubble at time, t = 2.5, 5, 7, 9 and 11 respectively, for Ga = 50, Bo = 15, r = 7.4734 × 10−4 and m = 8.5136 × 10−6.

Full size image

A typical breaking drop, with its associated streamlines is shown in figure 11. As discussed above, the breakup is very different from that of a bubble, since the primary vortical action is outside and causes a thinly stretched cylindrical, rather than toroidal shape.

Figure 11
figure 11

Streamlines in and around the drop at time, t = 4.5, 6 and 7.5 respectively, for Ga = 50, Bo = 5, r = 10 and m = 10.

Full size image

The vortex in the wake of the drop tends to stretch the interface (and surface tension is not high enough to resist the stretching) which leads to an almost uniformly elongated backward bag. New eddies are formed due to flow separation at the edge to the “bag” and a toroidal rim is detached after some time from this bag. A drop too responds to Bond number, but the response is shown in terms of an early break-up at high Bond numbers, as seen in figure 12. The shape at break-up too evolves with the Bond number, as shown.

Figure 12
figure 12

Variation of break-up time with Bond number for Ga = 50, r = 10 and m = 10.

Full size image

Conclusions

A bubble and a drop, starting from rest and moving under gravity in a surrounding fluid, cannot in general be designed to behave as one another's mirror images (one rising where the other falls). We have shown that the underlying mechanism which differentiates the dynamics is that the vorticity tends to concentrate in the lighter fluid and this affects the entire dynamics, causing in general a thicker bubble and a thinner drop. However, if inertia is small, surface tension is large and a drop is only slightly heavier than its surrounding fluid, a suitably chosen bubble can display dynamics similar to it. In this limit, the Hadamard solution can be exploited to design a bubble with its density and viscosity suitably chosen to yield the same acceleration at any time as a given drop. We are left with an interesting result: while a solid ‘bubble’ can never display a flow history which is the same as a solid ‘drop’, a Hadamard bubble can. Also, although density differences are small, the Boussinesq approximation cannot lead us to the closest bubble for a given drop.

We find numerically that a similarity in bubble and drop dynamics and shape is displayed up to moderate values of surface tension and inertia, so long as the density ratio is close to unity. In axisymmetric flow, the vorticity concentrates near the base of the bubble, which results in a pinch-off at the centre whereas the cup-like shape displayed by a drop and the subsequent distortions of this shape due to the vorticity in the surrounding fluid, encourage a pinch-off at the sides. Bubbles of Ga higher than a critical value for a given Bo will break up at an inertial time between 2 and 3. For Ga or Bo just below the critical value, oscillations in shape of the same time scale occur before the steady state is achieved.