Introduction

Waves are present in numerous geophysical gravitational flows1,2,3 (Fig. 1), including debris flows on Earth4,5,6, volcanic lava flows on Mars7, and granular avalanches on the Moon8. Snow avalanches also produce waves that magnify the avalanche danger9. Indeed, waves not only signify higher local flow height but also larger local velocity, both factors increasing the destructive impact on infrastructure10,11. According to debris flow field measurements, the wave velocity can be twice the velocity of the flow front12, and similar measurements performed in snow avalanches show that pressure maxima coincide with the passage of waves13. In addition to the danger of the waves themselves, they can induce further hazardous effects on the surrounding medium. For example, the waves in the dense core of a powder snow avalanche can serve as a source of fierce oscillations of the surrounding powder cloud14.

Fig. 1: Waves in geophysical gravitational flows.
figure 1

a A debris flow in Jiang Jia Gully in China (photo from Dongchuan Debris Flow Observation and Research Station); b A lava flow erupted at Kilauea in Hawaii in USA (photo from U.S. Geological Survey); c A bidisperse granular avalanche11; d Deposit of a snow avalanche in Yule Creek Valley in USA (photo from Colorado Avalanche Information Center).

Full size image

Although waves largely control the destructive capacity of a snow avalanche, because of the complicated multiphysical processes (e.g., erosion, deposition, collision, ground-induced flow instability) that characterize avalanche dynamics9,15, it is notoriously challenging to simulate realistic wave features with numerical approaches. Existing numerical investigations on real-scale snow avalanches predominantly adopt depth-averaged shallow water equations combined with constitutive laws (e.g., Voellmy model, Bingham model) developed based on the macroscopic flow behavior of snow avalanches, which can efficiently reproduce the runout distance and velocity of real avalanches16,17,18,19,20,21. With more sophisticated constitutive models accounting for viscous dissipation and changing friction regimes (e.g., static, intermediate, and dynamic), different types of waves have been recovered under idealized conditions with uniform and steady incoming flows22,23,24,25,26,27. Nevertheless, snow avalanches in the field are typically non-uniform and unsteady, which introduces an additional difficulty to the problem.

Large wave activity in snow avalanches was suspected and recently confirmed by measurements with the GEODAR (GEOphysical flow dynamics using pulsed Doppler radAR) installed at the Vallée de la Sionne full-scale experimental site (VdlS) in Switzerland28,29. While large surges could be attributed to the interaction of several moving avalanche branches on the complex topography, or secondary releases, smaller waves occurring at the surface of the dense basal layer have been hypothesized to be instability processes, such as roll-wave activity. However, so far there is no direct evidence of the real nature of the waves, either from field observations or numerical modeling.

Granular experiments conducted in the laboratory have recently shown that waves observed from the surface of the dense layer can be different in nature30,31. This study, in particular, distinguishes between roll-waves, which are a series of fully mobilized waves, and erosion-deposition waves, which are characterized by stationary regions between wave crests23. Based on small-scale chute flow experiments and related numerical simulations, the formation of different types of waves is associated with the initial height of the incoming flow and the slope inclination23,32,33. According to this study, we hypothesize that waves in snow avalanches may be of a similar nature, and as the height of a snow avalanche changes over time and space, the transition between roll-waves and erosion-deposition waves may occur.

Here, we aim to contribute to a better understanding of wave activity in snow avalanches with consideration of real terrain and snow entrainment along the path, by using a hybrid Eulerian-Lagrangian approach called the material point method (MPM) and comparing these simulations to a snow avalanche dataset, measured in 2015 at VdlS. Using the MPM approach, roll waves were observed in simulated avalanches on ideal parabolic tracks partially covered with erodible snow34. In this study, the snow properties of the avalanche are firstly calibrated by simulating small-scale chute flows of snow and comparing the simulated deposit height with the field data. Then, the avalanche on real terrain is modeled with the calibrated snow properties. By virtue of the MPM and an elastoplastic constitutive model recently developed for snow35, we are able to capture a complex wave activity including roll-waves, erosion-deposition waves, and their transitions, in real scale. Finally, the simulated wave features are analyzed in conjunction with the field data measured with FMCW (frequency-modulated continuous wave) radars36 and the GEODAR29. The Froude number and mass of individual waves in the avalanche are associated with the slope angle of the VdlS terrain.

Results

Calibration of snow properties

To calibrate the input snow properties (e.g., friction, cohesion, strength) for our simulations, numerical experiments were conducted with the MPM (detailed in Methods). The parameter calibration is performed on a small-scale setting for computational reasons. These simulations are run on an inclined plane, the slope angle θ which can be varied. The height of the deposited snow h on the ideal slope, calculated along the normal direction of the bed, is extracted and compared with similar measurements performed in the deposits of full-scale avalanches37 as well as fitting curves using the Pouliquen model38. As observed from Fig. 2, the results from the small-scale MPM simulations using the parameters in Table 1 agree well with the field data, both showing a negative correlation between the height of the deposited snow and the slope angle. The fitting curves show an exponential increase towards small slope angles (e.g., lower than 22∘ and 23∘ in our cases)37,38. From the comparison with the field data, we obtained calibrated snow properties for our numerical modeling (Table 1). These snow properties are then used to model a real-scale avalanche that occurred at the VdlS in 2015 (see “Methods”). The MPM real-scale simulated average deposit height as a function of slope is shown in red in Fig. 2. In general, the real-scale simulation shows good agreement with the field data. The variation of h at the same slope angle can be reflected in the error bars, whose length depends on the local terrain feature and the avalanche dynamics. For example, the lower error bar at θ = 28∘ is due to the local convex terrain, which makes the avalanche more difficult to stop and thus reduces the deposition height. The MPM simulation underestimates the height of deposited snow at θ = 23∘, which might be also due to the local convexity of the terrain. The agreement between the real-scale simulation and the field data back-verifies the calibrated snow properties from the small-scale simulations and proves the capability of the numerical model in bridging the results at different scales.

Fig. 2: Evolution of the height of deposited snow h with the slope angle θ.
figure 2

The field data were collected at the VdlS test site37. The fitting results for the field data were obtained from the Pouliquen model38 \(\tan \theta =\tan {\theta }_{1}+(\tan {\theta }_{2}-\tan {\theta }_{1})\exp (\frac{-h}{L})\). The fitting parameters are θ1 = 22. 5∘, θ2 = 34. 4∘, L = 0.19 m for avalanche 81737, and θ1 = 21. 4∘, θ2 = 34. 7∘, L = 0.31 m for avalanche 81637. The small-scale simulations are the chute flows modeled with the MPM. The coefficient of determination between the field data 816 and the small-scale MPM results is 0.972. The real-scale simulation with MPM corresponds to the VdlS avalanche of 2015, the medium height (triangles) is shown with the 25th and 75th percentiles (whiskers). The coefficient of determination between the field data 816 and the real-scale MPM results is 0.969.

Full size image
Table 1 Snow properties adopted in the simulation.
Full size table

Roll-waves and erosion-deposition waves in the VdlS avalanche

Figure 3a shows the VdlS terrain, the release zone, and the flow path of the avalanche of 2015. A video of the field avalanche can be found in the supplementary materials (video 1). The avalanche is simulated in two dimensions (2D), neglecting variations along the flow width, to save computational cost. The three-dimensional (3D) flow path shown in Fig. 3a was projected onto a 2D trajectory respecting the original total flow distance and slope angle.

Fig. 3: Topography used for avalanche simulation, with both observed and modeled wave activity.
figure 3

a Terrain of the VdlS test site, the release zone in blue and the flow path in black, the blue dot shows the position where a frequency-modulated continuous wave radar is buried in the ground; b Roll-waves observed in the dense core of a powder snow avalanche measured at the Flüela Pass, Switzerland29; c Roll-waves and erosion-deposition waves observed in the simulated VdlS avalanche.

Full size image

In the simulation, the heights of the release slab and the erodible snow cover, defined along the normal direction of the bed, are set to 1 m and 1.5 m, respectively, according to field measurements. The modeled snow properties are summarized in Table 1. The properties of the released snow are calibrated from the small-scale chute flow simulations in the previous section, which naturally give a cold snow avalanche as observed in the field. As the avalanche is cold, it is mainly governed by expansion and separation, instead of compression and densification. Therefore, the bulk density of the avalanche becomes smaller than the initial density of the released snow during the flowing process. The erodible snow cover has a different set of properties to guarantee its initial stable state. A detailed explanation of the properties used in the simulations can be found in the Methods section.

Numerical simulation of the 2015 avalanche (see supplementary video 2), shows that both roll-waves and erosion-deposition waves can occur on the VdlS topography (Fig. 3c). Similarly to the laboratory experiments22,23, the roll-waves in our simulations (Fig. 3c) are characterized by moving particles between the wave crests. In contrast, the erosion-deposition waves have stationary particles between individual waves. In our simulations, we can additionally observe that while both roll-waves and erosion-deposition waves erode particles at the front, deposition at the wave tail only happens in the erosion-deposition waves (see supplementary videos 3 and 4). Based on the simulations, there is no clear correlation between the flow height and the wave type (i.e., roll wave, erosion-deposition wave), differing from the ideal chute flow experiments23. Indeed, the more complex condition considered in this study not only has flow instabilities caused by the snow but also that induced by the irregular VdlS terrain. The effect of the terrain heterogeneity apparently weakens the correlation between the flow height and the wave type. In the simulated avalanche, frontal ploughing is clearly observed (supplementary video 5). Due to compression, the bed particles downstream of the flow front move even though they do not have direct contact with the avalanche. These moving bed particles are then caught by the avalanche and become part of the frontal wave.

Spatial-temporal wave evolution

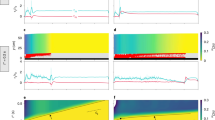
Figure 4 shows the flow height evolution at the location of the FMCW radar and the variation of wave features in the spatio-temporal space, where the flow height is measured normally to the bed. Figure 4a, c show the waves from the two-dimensional simulation, while Fig. 4b, d show the data for the 2015 avalanche collected with FWCW radars (panel b) and the GEODAR (panel d). The y-axis in Fig. 4a, b is the vertical distance between a snow particle and the ground surface at the FMCW location (Fig. 3a). The range in Fig. 4c, d denotes the distance from the bunker where the GEODAR is located. The radar characteristics and the VdlS avalanche are described in the Methods. Different colorbars are used in the numerical results (Fig. 4a, c) and the field ones (Fig. 4b, d), since the colored quantities do not have the same physical meaning. Particularly, in Fig. 4a, c, the colorbar shows the avalanche velocity in the simulation, while in Fig. 4b, d, the colorbar reflects the intensity of the reflected radar signals (see Field measurements).

Fig. 4: Flow height evolution at a fixed position along the avalanche path and the variation of wave features in the spatial-temporal space from the two-dimensional MPM simulation and the field investigation.
figure 4

a Flow height evolution at range 1271 m from the simulation colored with velocity; b Flow height evolution at range 1271 m from FMCW radar measurements colored with the intensity of the radar signal; c spatial-temporal variation in the velocity of the simulated avalanche; d MTI (Moving Target Identification) image of the field avalanche obtained from the GEODAR, the yellower portions indicate areas without moving snow, the leading edge of the avalanche is indicated by an abrupt transition to darker color intensity.

Full size image

The flow height evolution from the simulation in Fig. 4a shows a large frontal surge arriving at the monitoring point at 77 s. It is followed by a series of smaller waves from 88 s to 146 s. The frontal surge is characterized by distinct internal fluctuations at the free surface as shown by the inset of Fig. 4a, indicating the possible occurrence of roll-waves inside the surge. The frontal surge has the highest height and largest velocity compared to the subsequent waves. These characteristics are in agreement with the field measurements in Fig. 4b. Furthermore, the maximum height monitored in the simulation is 8.2 m (Fig. 4a), which comes from the scattered particles of the frontal wave. In comparison, the maximum height measured in the field is 8.8 m, this higher height in the field is due to the powder cloud, which is not considered in the simulation. The simulated maximum height of the dense core is 6.2 m, which has satisfactory consistency with the field data (6.0 m in Fig. 4b). The height of the remaining snow on the slope is 0.5 m in the simulation, agreeing well with the field data. The later waves in the simulation (from 88 s to 146 s in Fig. 4a) have stationary particles between the wave crests and thus can be classified as erosion-deposition waves. To confirm that the waves observed in the simulation are due to physical reasons instead of numerical instabilities, two groups of simulations varying snow friction M and slope angle θ were conducted with other numerical parameters fixed (see supplementary note 1). It is found that waves occur in cases with low snow friction or high slope angle, and the occurrence of waves could be associated with the Froude number. A more detailed analysis can be found in supplementary note 1.

In addition to the roll-waves and erosion-deposition waves at the monitoring point, Fig. 4c further shows how the wave activity evolves over the entire spatial-temporal space. Waves 1–5 start close to the release position near range = 2022 m, while waves 6 –14 emerge only farther downstream. The frontal surge (wave 1) shows more pulsing activity than the subsequent waves, which might be due to the higher front velocity and the presence of internal waves overtaking each other at the front as observed in the field measurements9. Wave 2 has a turning point near range = 1122 m, which is related to the local concave terrain. During the evolution of the waves, roll waves (e.g., lower inset in Fig. 4c), erosion-deposition waves (e.g., upper inset in Fig. 4c), and transitions between them are captured. Details of the waves at specific ranges and moments, corresponding to the inset marked in red in Fig. 4c, are visualized in Fig. 3c. Behind wave 1, there are smaller waves that originate from wave 1 and then move away from wave 1. Taking wave 6 as an example, it starts near range=1006 m, and its distance from wave 1 increases with time. This separation process indicates the transition from roll waves to erosion-deposition waves. In contrast, there are waves that come closer over time until they merge. For example, from range = 1036 m to range = 668 m, there is an erosion-deposition wave that initially precedes wave 7, but is soon swallowed by the latter. The erosion-deposition wave in turn becomes part of the roll wave. All the waves in Fig. 4c stop before or close to range = 100 m, showing a consistent runout distance with the field avalanche (Fig. 4d).

Note that, in the 3D real case, there was a faster surge moving along another flow channel not considered in the flow path of the 2D simulation, therefore, the first surge corresponding to that in the simulation is behind the front in Fig. 4d. As shown in Fig. 4b, the front in Fig. 4d did not pass the position where a FMCW radar is buried to measure the flow height evolution. The averaged velocity of the first surge from the simulation is quantitatively compared with the field data. From Fig. 4c, the inclination of the first surge indicates the averaged velocity of 32.7 m/s, which has a relative error of 3.5% compared with the field data (33.9 m/s in Fig. 4d). Although we were able to reproduce quantitatively some key features of the avalanche such as the front velocity and flow height, Fig. 4 also shows obvious differences, especially concerning wave activity in the tail of the avalanche. These differences will be discussed in the “Discussion”. The numerical results in this study reveal that roll waves, erosion-deposition waves, and their transitions can occur in a single avalanche.

The dynamic behavior of relatively large waves (i.e., waves 1–14 in Fig. 4c) is analyzed in Fig. 5. The extraction of the waves is detailed in Methods. The Froude number, defined as the ratio of the flow inertia to the gravitational field, is shown in Fig. 5a. Wave 1 has the largest Froude number, as it is the frontal wave with the highest velocity (Fig. 4c). The Froude number of wave 2 is initially similar to that of wave 1 (range between 1980 and 1712 m), and then becomes smaller mainly due to the reduction of its velocity. The remaining waves have relatively small Froude numbers, among which waves 6&7 share similar Froude numbers with wave 2 when range <1112 m. All the Froude numbers are smaller than 4.7, which is consistent with the field avalanches at Vallée de la Sionne (typically smaller than 6)39. The wave mass m normalized by the mass of the released snow m0 is shown in Fig. 5b. The frontal wave has the largest mass, which reaches 2.5 times the release mass. Indeed, the high flow velocity and Froude number give a larger kinetic energy of the moving mass, which enhances the entrainment of the snow cover. The sudden reduction in the mass of wave 2 at range = 1122 m is due to the locally concave terrain, which also causes the sudden deceleration of wave 2 in Fig. 4c. The increase of wave mass for waves 6&7 is associated with the merging of waves ahead of them.

Fig. 5: Behavior of relatively large waves in the simulated avalanche.
figure 5

a Evolution of Froude number of individual waves; b Evolution of the normalized mass of individual waves, where m and m0 are, respectively, the wave mass and the mass of the released snow (m0 = 19640 kg); c Evolution of the normalized Froude number of individual waves along with the slope angle of the terrain; d Evolution of the average normalized Froude number of all the waves in Fig. 5c and the slope angle of the terrain.

Full size image

Interestingly, by normalizing the Froude number with the wave mass and the mass of the released snow (\({{{{{{{\rm{Fr}}}}}}}}/{(m/{m}_{0})}^{0.2}\)), a roughly unified trend of the waves can be obtained (Fig. 5c). Despite local spikes, the general trend of the waves is close to the slope angle evolution of the terrain. This agreement is more obvious when the normalized Froude numbers of the waves are averaged (Fig. 5d). It can be concluded that the normalized Froude numbers \({{{{{{{\rm{Fr}}}}}}}}/{(m/{m}_{0})}^{0.2}\) of all the investigated waves collapse to a single trend controlled by the slope angle of the terrain, where the exponent 0.2 is obtained based on data fitting. In addition, the inset of Fig. 5d shows the positive correlation between the normalized Froude number and the slope angle. This strong correlation between the Froude number and the terrain can be attributed to two aspects. First, according to the definition of Froude number (Eq. (6)), it is positively correlated with the slope angle. Secondly, Froude number increases with the growth of velocity, which also has a positive relation with the slope angle. To further verify the correlation of the dynamic wave behavior in terms of the Froude number and the terrain, the average slope angle of the VdlS terrain is calculated to be 28∘, and is used in a simulation with a constant slope angle. It is found that the normalized Froude number of the avalanche waves fluctuated around a constant value, showing the governing effect of the constant slope angle (see supplementary note 2).

Discussion

This study helps to fill the research gap on waves and their transitions in real-scale, unsteady, and non-uniform avalanches. Our numerical approach considers realistic snow properties calibrated with the field data and serves as a new methodology to bridge results at different scales. In addition to the roll waves already observed from field avalanches, the erosion-deposition waves speculated for field avalanches9,33 and transitions between roll waves and erosion-deposition waves have been captured from our simulation. Moreover, a unified trend of all the investigated waves, controlled by slope angle, is revealed with the Froude number, the wave mass, and the mass of the released snow. In addition to snow avalanches, it is suspected that other gravitational mass movements such as debris flows and lava flows40,41 have similar wave activity, and this study offers an unprecedented pathway for their exploration. Interestingly, our numerical model does not explicitly consider frictional hysteresis as required in previous depth-averaged simulations to recover erosion-deposition waves and roll-waves under ideal conditions22,23. Nevertheless, the frictional hysteresis of the material is hidden in our model and can be reflected by the combined effect of the friction coefficient M and the tension/compression ratio β (see Methods). When a moving snow particle stops, its friction changes from the dynamic regime to the static regime, and the stopping is affected by its cohesion.

While main surges show similar characteristics in our simulation and field measurements (Fig. 4), it is noticed that the tail part of the simulated avalanche differs from that in the field, as we clearly observe waves in the simulation that are absent in the field plot (Fig. 4d). This difference might be attributed to three causes. Firstly, the simulation results come from a 2D modeling for computational efficiency, while, in contrast, the MTI image is the averaged data over the 3D terrain, as the GEODAR collects information over a 30°-wide sector and averages the points with the same range or line-of-sight distance9,13. Secondly, the simulation data are elementary kinematic quantities like velocity and flow height, while the radar signal represents the back-scatter intensity of moving mass and depends on the density, particle size, and water content of the flow. Thirdly, the constitutive model used in this study does not consider the change of snow properties with temperature, and the snow properties, including friction and cohesion, are kept constant throughout the entire flowing process of the avalanche.

The change of snow properties can affect the wave behavior (e.g., wave number, wave velocity, wave transition) as analyzed in supplementary note 2. The waves obtained in the simulated VdlS avalanche are due to the setup in this study (e.g., terrain, snow properties), by changing these values  the tail waves could disappear as normally observed for snow avalanches. The snow properties adopted in our study were obtained based on the field data and will need to be further calibrated with experimental tests such as triaxial compression and direct shear tests. To recover the wave phenomena in granular flows, the constitutive model adopted in this study is not the only option. For example, the roll waves of two-phase debris flows were recovered by using the Mohr-Coulomb plasticity for the granular phase and a viscous Newtonian fluid for the fluid phase42. In addition, the Herschel-Bulkley model and the depth-average μ(I) rheology model can also reproduce the roll waves and erosion-deposition waves in granular flows22,23,43.

A preliminary 3D simulation of the VdlS avalanche was conducted (see supplementary note 3). However, due to the missing field data and the artificial boundary conditions adopted in the 3D simulation, it is difficult to do a one-to-one comparison of the simulation result with the field data. In the future, more insight into waves in real avalanches can be obtained by improving computational efficiency and developing a more sophisticated constitutive model that includes fluidization, sintering, and thermodynamic effects for three-dimensional numerical simulations, and by revealing complicated wave behavior in field avalanches with advanced measurement techniques offering clear kinematic information. The rate-dependency and non-local effects of granular flows44,45,46 will need to be considered for more accurate modeling of snow avalanches.

The current comparison between the numerical and field results mainly focuses on the dense part of the avalanche, to fully capture the features of dry avalanches, the dilute powder cloud needs to be considered as well. Moreover, this study shows that topography has a significant correlation with dynamic wave behavior in avalanches. A preliminary study of cases with different slope angles proves that the steeper the slope angle, the longer the length of the waves in the avalanche (supplementary note 2). To further explore the interaction between terrain and avalanche waves, different terrain features, including slope angle, curvature, and roughness, need to be systematically investigated in the future.

Methods

Numerical simulations

The numerical framework adopted in this study includes two key components, namely, a hybrid Eulerian-Lagrangian approach called the MPM47,48 and a large strain elastoplastic constitutive model developed for snow35. MPM uses Lagrangian particles to carry material states and an Eulerian grid to solve the material motion and update these states. By virtue of the hybrid nature of MPM, it can effectively and efficiently handle large-deformation problems such as landslides and snow avalanches. These large-deformation problems could be solved by other methods as well49, including discrete element method (DEM), particle finite element method (PFEM), and smooth particle hydrodynamics (SPH). In MPM, the material motion is governed by mass and momentum conservation:

$$\frac{D\rho }{Dt}+\rho \nabla \cdot {{{{{{{\bf{v}}}}}}}}=0$$
(1)
$$\rho \frac{D{{{{{{{\bf{v}}}}}}}}}{Dt}=\nabla \cdot {{{{{{{\boldsymbol{\sigma }}}}}}}}+\rho {{{{{{{\bf{g}}}}}}}}$$
(2)

where ρ is density, t denotes time, v is velocity, σ is the Cauchy stress, g is the gravitational acceleration. As the mass of each particle does not change with time in MPM, the mass balance in Eq. (1) is naturally satisfied. The momentum conservation in Eq. (2) needs to be solved in combination with the elastoplastic constitutive model, which relates the Cauchy stress σ and the strain as follows:

$${{{{{{{\boldsymbol{\sigma }}}}}}}}=\frac{1}{J}\frac{\partial \Psi }{\partial {{{{{{{{\bf{F}}}}}}}}}_{E}}{{{{{{{{\bf{F}}}}}}}}}_{E}^{T}$$
(3)

where Ψ is the St. Venant-Kirchhoff energy density calculated as \(\Psi =\mu {{{{{{{\rm{tr}}}}}}}}({{{{{{{{\boldsymbol{\epsilon }}}}}}}}}^{2})+0.5\lambda {{{{{{{\rm{tr}}}}}}}}{\left({{{{{{{\boldsymbol{\epsilon }}}}}}}}\right)}^{2}\), μ and λ are Lamé parameters, ϵ is the elastic Hencky strain, FE is the elastic part of the deformation gradient F which can be decomposed into elastic and plastic components as F = FEFP, and \(J=\det ({{{{{{{\bf{F}}}}}}}})\).

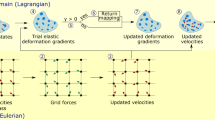
The MPM algorithm is illustrated in Fig. 6a. At the beginning of a simulation, the initial states of the material are assigned to the Lagrangian particles. These particle states are transferred to the grid nodes, and each grid node receives weighted mass and velocity from its surrounding particles (step 1 in Fig. 6a). Then, the equation of motion in Eq. (2) is solved with the Eulerian grid, and each grid node updates its velocity and position (step 2 in Fig. 6a). The new states of the grid nodes are transferred back to the particles (step 3 in Fig. 6a) so that the particles can further update their velocities and positions (step 4 in Fig. 6a). Meanwhile, the deformation of the particles can be updated according to the elastoplastic constitutive model, which is composed of a Cohesive Cam Clay (CCC) yield surface, a hardening law, and an associative flow rule. The adopted constitutive law can recover the mixed-mode failure50 of snow, solid-fluid transitions51, and density variations in avalanches.

Fig. 6: MPM methodology.
figure 6

a Overview of the MPM algorithm; b The cohesive (in green and red) and cohesionless (in gray dot) Cam Clay yield surface in the p−q space; c The hardening law controlling the pre-consolidation pressure p0 with the volumetric plastic strain \({\epsilon }_{v}^{p}\).

Full size image

As shown in Fig. 6b, the adopted CCC yield surface (in green and red) in the p-q space is obtained by adjusting the cohesionless Cam Clay yield surface (in gray dot) and is expressed as:

$$y(p,q)=(1+2\beta )\, {q}^{2}+{M}^{2}(p+\beta {p}_{0}) \, (p-{p}_{0})$$
(4)

where p is the mean effective stress (or pressure) and q is the von Mises stress. Given the Kirchhoff stress tensor τ and the dimension d, the pressure p can be calculated as \(p=-{{{{{{{\rm{tr}}}}}}}}({{{{{{{\boldsymbol{\tau }}}}}}}})/d\). A positive p denotes compression, and p < 0 corresponds to tension. The von Mises stress q is defined as q = (3/2s: s)1/2, where s is the deviatoric stress tensor calculated as τ + pI and I is the identity matrix. If q > 0, shear occurs. The pre-consolidation pressure is denoted as p0, which determines the size of the yield surface according to Eq. (4) and can be used to obtain the isotropic tensile strength βp0, where β controls the cohesion and is the ratio between tension and compression. The slope of the critical state line M reflects the internal friction35. Given the yield criterion in Fig. 6b, the stress state of the material can never be outside the yield surface (non-admissible). However, the trial stress states during the numerical calculation can go beyond the yield surface (e.g., points A&B in Fig. 6b) when plastic behavior occurs, under which condition we need to project the trial p-q state back to the yield surface (e.g., points \({A}^{{\prime} }\)&\({B}^{{\prime} }\)) using a flow rule and adjust the yield surface according to a hardening law. In this study, an associative plastic flow rule52,53 is used based on a previous study on snow35. As shown in Fig. 6b, the trial stress states (points A&B) are projected to the yield surface (points \({A}^{{\prime} }\)&\({B}^{{\prime} }\)) following a path perpendicular to the tangent line to the yield surface. In doing so, the principle of maximum plastic dissipation is followed and the plastic dissipation rate is maximized.

To account for the varied material strength due to the plastic behavior, a hardening law needs to be applied as below:

$${p}_{0}=K\sinh (\xi \max (-{\epsilon }_{v}^{p},0))$$
(5)

where K is the bulk modulus, ξ the hardening factor, and \({\epsilon }_{v}^{p}\) the volumetric plastic strain. It is assumed that K and ξ are constant, and the change in p0 solely rests on \({\epsilon }_{v}^{p}\). As shown in Fig. 6b, c, when the trial p-q state is on the left side of the apex of the yield surface (e.g., Point A), the plastic strain increases (\({\dot{\epsilon }}_{v}^{p} \, > \, 0\)) and p0 decreases. This reduction of p0 leads to softening of the material and allows fracture under tension. In contrast, when the plastic strain is compressive (\({\dot{\epsilon }}_{v}^{p} \, < \, 0\), as at Point B), p0 increases, which gives hardening and more elastic responses under compression.

According to the previous study of the effect of snow properties on the dynamics of snow avalanches, it is found that the friction coefficient M and the tension/compression ratio β are the most critical in controlling the behavior of the avalanches54. Therefore, M and β need to be carefully determined. Based on field investigation (see Field measurements), the VdlS avalanche explored in this study is dry, indicating low density and no cohesion. Thus, the snow density ρ and tension/compression ratio β are assumed as 100 kg m−3 and 0, respectively. According to the snow density, relevant snow properties, including Young’s modulus E, Poisson’s ratio ν, hardening factor ξ, and pre-consolidation pressure at the initial state \({p}_{0}^{ini}\), are determined, whose values are summarized in Table 1. To obtain the friction coefficient M, all other parameters in Table 1 are fixed, and small-scale simulations with different M were conducted to get the evolution of the height of deposited snow h with the slope angle θ for comparison with the field data and theoretical prediction in Fig. 2.

Particularly, small-scale snow collapses on ideal slopes with constant inclination were simulated as shown in Fig. 7. The length scale of the release zone in Fig. 7 is significantly smaller than the real avalanche at VdlS, therefore the simulations are called small-scale. The setup in Fig. 7, instead of real-scale modeling on complex terrain, is used to greatly save computational cost. A block of snow is initially placed at the top of an inclined slope and is then released to collapse under gravity. The snow friction M is firstly varied from 0.8 to 1.0 with an interval of 0.1. It is found that M = 0.8 and M = 0.9 underestimate the height of the deposited snow h, while M = 1.0 gives overestimated h (see supplementary note 2). Therefore, M = 0.95 was used, with which the agreement between the simulation results and the field data is satisfactory as shown in Fig. 2. When M is fixed to 0.95, the initial height of the snow sample h0 and the slope angle θ are varied to obtain the relation between the height of deposited snow h and the slope angle θ in Fig. 2.

Fig. 7: Illustration of the setup of the small-scale numerical simulations for calibration of snow properties.
figure 7

The initial length and height of the snow sample are l0 fixed at 5 m and h0, respectively. The slope angle is denoted as θ. The height of the final deposit h is defined as the maximum height of the deposit since it is the critical value below which no flow is possible38,56.

Full size image

Considering a snow block on a slope with an initially gentle inclination, if the slope angle increases gradually, the minimum slope angle at which the snow block will collapse entirely and flow downward is called θstart. On the other hand, the maximum slope angle at which the snow can remain stable is called θ and the corresponding deposited snow height is called h. In Fig. 2, we vary θ from 22∘ to 33∘ and obtain their corresponding h. For each (h, θ), a group of simulations were conducted. For example, to get the datum point (22∘, 0.859 m), the initial height of the snow sample h0 is fixed to 1 m, and the slope angle is decreased from 25∘ to 20∘ with an interval of 1∘. It is found that when the slope angle is larger than 22∘, the snow sample entirely collapses. Therefore, 22∘ is determined as θ, and the height of the partially collapsed snow when θ = 22∘ is 0.859 m (lower panel in Fig. 7). This height is obtained according to the position of the top particles in the collapsed snow. Similarly, by conducting another group of simulations with h0 = 0.9 m, the datum point (23∘, 0.749 m) can be obtained. With 12 groups of simulations, the deposit height h when θ ranges from 22∘ to 33∘ can be determined as summarized in Table 2 and plotted in Fig. 2.

Table 2 Model parameters in the small-scale simulations.
Full size table

For the small-scale simulations, the background mesh cells have identical size (0.01 × 0.01 m). The total particle number varies from around 2 × 104 to 2 × 105 depending on the initial height of the sample. The time step is 5 × 10−5 s, determined according to the CFL condition and the elastic wave speed. The computational time for one simulation with real-time of 50 s is from around 50 mins to 4.5 h on a 36-core Intel i9 CPU (3.0 GHz) desktop computer. Using the same computer, the simulation of the VdlS avalanche takes 3.3 h for the real-time of 200 s, with a spatial resolution of 0.2 m for the background mesh and a time step of 0.001 s. The total particle number in the simulation of the VdlS avalanche is around 0.44 million.

Field measurements

The avalanche investigated in this study was artificially released at the VdlS test site on 3 February 2015 at 10:20. Owing to snow precipitation prior to the avalanche, 0.95 m of new snow was accumulated on a 1.35 m thick snow cover composed of weakly bonded faceted crystals at the surface and depth hoar layers at the base9. A few hundred meters north of the test site, a weather station (Donin du Jour at 2390 m asl.) measures the air temperature and is assumed to be representative of the meteorological conditions of the avalanche. As the air temperature was below -10 ∘C, consolidation of the new snow was prevented. The snowpack was stable until the avalanche was triggered artificially. The avalanche was filmed by a thermal camera, and local temperatures were manually measured in the deposition zone. According to these field measurements, the temperature of the snow in the avalanche was at least below –5 ∘C, indicating that the avalanche could be dry and with low water content. The field data in Fig. 4b, d were obtained with a FMCW radar55 and a phased-array radar system called GEODAR (GEOphysical flow dynamics using pulsed Doppler radAR)36, respectively.

The FMCW radar is buried in the ground at a position within the avalanche track at 1900 m asl, and looks upward through the snow above. In particular, the radar measures a vertical cross-section of the avalanche during a defined time period and calculates the time it takes the signal to return after being reflected from a snow particle or clump. The intensity of the received signal can be therefore obtained, and its corresponding height provides information regarding the avalanche height distribution. The frequency of the transmitted signals is periodically increased from 8.5 to 10.25 GHz during the first third of the signal. This part of the signal is used to determine the flow height of the avalanche. The signal then remains constant at 10.25 GHz and the Doppler effect is measured to detect particle velocities perpendicular to the slope. The broadcasted signal has a frequency of 120 Hz controlled by a clock of the FMCW radar55. The main error associated with the FMCW radar measurements concerns multiple reflections, especially in the stationary snowpack. When the signal is reflected from a layer, it is not always necessarily reflected straight back to the radar. At layer boundaries, the signal may rebounce causing the signal to appear as though it was reflected from another layer higher up in the snowpack. This implies that the evaluation of the position of the free surface of the snow cover before the avalanche needs to be considered as an approximate value.

The GEODAR is installed in the bunker at the Vallée de la Sionne test site and monitors all the avalanche activity at the site, covering nearly the whole slope from the top of the mountain, at range 2700 m to the bottom of the valley, close to the bunker, at range 120 m29. The radar collects information over a 30o-wide sector, which is averaged over all points at the same line-of-sight distance from the antenna. The frame rate and range resolution of the GEODAR measurement are 111 Hz and 0.75 m, respectively. The radar operates with a wavelength of 57 mm (5.3 GHz), thus it can see snow particles or clumps in the avalanche that are larger than the radar wavelength. Such particles are present in the dense basal layer or may be found in the intermittent region of powder snow avalanches13. The millimeter-sized snow crystals in the powder cloud are too small to reflect the radar signal to a significant degree. Therefore, the powder cloud is expected to be transparent for the radar beam. The signal from eight receiving antennas is averaged to improve the signal-to-noise ratio. GEODAR measurements are displayed using Moving Target Identification (MTI) plots. An MTI plot is a spatio-temporal plot that shows any change in radar reflectivity at a particular time and range. An MTI plot distinguishes between moving and stationary parts inside the monitored slope.

Acquisition of simulation results

To obtain the information on individual waves in Fig. 5, a velocity higher than 3 m/s is used as a criterion to extract the main body of the waves, by which the slowly moving particles at the end of the waves are effectively eliminated while the particles in the main body of the waves are kept. The Froude number is defined as:

$${{{{{{{\rm{Fr}}}}}}}}=\frac{v}{\sqrt{gH\cos \theta }}$$
(6)

where v is the flow velocity, H is the flow height measured perpendicular to the terrain, and θ is the slope angle. To get the local Froude number Frc, the simulation domain in the range-time space (as in Fig. 4c) is discretized with a range interval of 2 m and a time interval of 1/12 s, using which the wave behavior in spatial and temporal dimensions can be accurately recovered with a reasonable post-processing cost. For each local cell in the range-time space, the average velocity of the snow particles in that cell is obtained as vc, and the height of the flowing particles Hc is calculated by extracting the surface of static particles from the free surface. The local Froude number can be obtained as \({{{{{{{{\rm{Fr}}}}}}}}}^{c}={v}^{c}/\sqrt{g{H}^{c}\cos {\theta }^{c}}\), where θc is the local slope angle. To alleviate local spikes, Fig. 5a shows the average Froude number of individual waves within 1 s. Specifically for one wave, it is calculated as \(\mathop{\sum }\nolimits_{i = 1}^{n}({{{{{{{{\rm{Fr}}}}}}}}}_{i}^{c})/n\), where n is the total cell number of the wave within the time interval of 1 s. Similarly, the mass of the wave m in Fig. 5b is the averaged one within 1 s. The slope angle evolution with a range in Fig. 5c, d is obtained with a range interval of 20 m. The change in the interval values gives different local variations (or spikes) but does not affect the overall trends in Fig. 5.