Abstract
Recent experiments demonstrate polaritons under the vibrational strong coupling (VSC) regime can modify chemical reactivity. Here, we present a complete theory of VSC-modified rate constants when coupling a single molecule to an optical cavity, where the role of photonic mode lifetime is understood. The analytic expression exhibits a sharp resonance behavior, where the maximum rate constant is reached when the cavity frequency matches the vibration frequency. The theory explains why VSC rate constant modification closely resembles the optical spectra of the vibration outside the cavity. Further, we discussed the temperature dependence of the VSC-modified rate constants. The analytic theory agrees well with the numerically exact hierarchical equations of motion (HEOM) simulations for all explored regimes. Finally, we discussed the resonance condition at the normal incidence when considering in-plane momentum inside a Fabry-Pérot cavity.
Similar content being viewed by others
Introduction
A series of recent experiments1,2,3,4,5,6,7,8,9,10,11,12,13,14 have demonstrated that chemical reaction rate constants can be enhanced11,12,13,14 or suppressed1,2,3,4,5,6,9,10 by coupling molecular vibrations to quantized radiation modes inside an optical microcavity. These surprising modifications happened under a “dark” condition without any external laser pumping, and the change in the chemical kinetics is attributed to the formation of vibrational polaritons (quasiparticles from the hybridization of the photonic and vibrational excitation)2,3. This phenomenon is referred to as the vibrational strong coupling (VSC) modified chemical reactivities, whose central feature is that when the cavity frequency ωc is in resonance with the bond vibration frequency ω0, the reaction rate constant can be enhanced or suppressed, usually up to 4–5 times compared to outside cavity rate constant10,11,14. This new strategy of VSC provides a novel avenue for synthetic chemistry through cavity-enabled bond-selective chemical transformations2,7,8,15,16,17 as one can selectively slow down one competing reaction over the target reactions by using cavities2,15.
Despite the encouraging progress in VSC experiments, we do want to point out that there are experimental efforts that try to reproduce the published VSC results but cannot find any apparent VSC modifications. One of them is an early attempt in ref. 18 to produce the enhancement of the hydrolysis reaction13 but not being successful. The second one was an attempt19 to reproduce the VSC enhancement on a hydrolysis reaction11 coupled inside an FP cavity, but cannot reproduce the effect. On the other hand, there is a preliminary attempt to reproduce the same hydrolysis reaction coupled to a plasmonic cavity and did find an enhancement of the rate constant20. In that same work20, the authors also tried to conduct this reaction inside the FP cavity and claimed to reproduce the VSC enhancement effect. We emphasize that ref. 20 has not been published but we trust readers’ own judgment on evaluating it. Overall, the reproducibility of these observed VSC effects remains an open experimental challenge and needs to be addressed in the future. Nevertheless, a good overview of technical concerns with the VSC flow cell experiment is given in ref. 21. In a different direction, recent experimental investigations22,23 on CN radical-hydrogen atom abstraction reaction do not reveal any noticeable change in the rate constant, even though the molecular system is under the strong coupling condition. However, these seemingly null results on the VSC effect have the potential to indirectly inform the fundamental mechanism and limitations of the VSC-induced rate constant modifications, and provide insights into when VSC will not be able to change rate constants.
From the theoretical side, a clear mechanistic understanding of VSC-modified ground-state chemical reactivity remains elusive, despite the recent theoretical developments24,25,26,27,28,29,30,31. In particular, there is no well-accepted mechanism or analytic rate theory31. There are many previous attempts to apply the existing rate theories (such as transition state theory (TST), Grote–Hynes theory27,32, quantum TST33, Pollak–Grabert–Hänggi theory28,30, and molecular dynamics simulations34, etc.), with the conceptual hypothesis that the cavity mode can be viewed and treated as regular nuclear vibrations27. However, none of them have successfully predicted the correct resonance condition or the sharp resonance peak of the rate constant distribution27,28,33,34. The fact that the VSC-influenced dynamics is sensitive to the quantum frequency ω0 also explains why the GH theory27,32, the PGH theory28, or q-TST rate theory33 cannot correctly predict the resonance condition because these theories are often based on a partition function expression that effectively sums over all possible vibrational frequencies, and does not explicitly contain the information of ω0, or they are more sensitive to the curvature of the potential which is not directly related to the quantum optical frequency. This suggests that the analytic rate theory of VSC Chemistry if that exists, might have a completely new analytic form31 that one has not encountered before in the theoretical chemistry literature.
Recent theoretical studies using a full quantum description of the vibrational degrees of freedom (DOF) and photonic DOF have successfully captured the resonance behavior under the single-molecule strong light–matter coupling regime35,36. We have used quantum dynamics simulations to reveal how cavity modes enhance the ground state reaction rate constant36,37. Specifically, we considered a double well potential coupled to a dissipative phonon bath35,36 as a generic model for chemical reaction, depicted in Fig. 1a. A simplified mechanism for the barrier crossing is described as follows
where k1 is the rate constant for the vibrational excitation of the reactant (left well), k2 is the rate constant of transition between the vibrational excited states of the left and right well, and k3 corresponding to the vibrational relaxation process in the right well. Through exact quantum dynamics simulation, we observed that36 k1 ≪ k2, k3, making \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) rate-limiting. Further, we found that the role of the cavity mode \({\hat{q}}_{{{{{{{{\rm{c}}}}}}}}}\) is to promote vibrational excitation and enhance k1. Using the steady-state approximation and Fermi’s Golden Rule (FGR) rate theory, the overall rate constant is approximated as k ≈ k1 = k0 + kVSC, where k0 is the outside cavity rate constant (which means in the absence of cavity modes throughout this paper), and kVSC is the cavity-enhanced rate constant. Including the cavity mode and its loss environment in an effective spectral density36, kVSC can be evaluated using FGR, expressed as
where τc is the cavity lifetime, ΩR is the Rabi splitting (for a single molecule coupled to the cavity, see Eq. (8)), ω0 is the vibrational frequency, and
is the Bose–Einstein distribution function, where β ≡ 1/(kBT) is the inverse of temperature T, kB is the Boltzmann constant. In typical VSC experiments1,10, ω0 ≈ 1200 cm−1 and room temperature 1/β = kBT ≈ 200 cm−1, such that βℏω0 ≫ 1 and n(ω) can be approximated as Boltzmann distribution. Under the lossy regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)), Eq. (2) agrees well with the numerically exact HEOM results, and has a sharp peak at
However, kVSC in Eq. (2) breaks down when \({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\) (the lossless regime) as it disagrees with the HEOM results (see Fig. 5 in ref. 36). This suggests that there will be a different mechanism for the VSC-modified rate constant under the lossless regime.
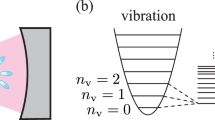
Top: Schematic illustration of molecules coupled to the radiation field inside a FP optical cavity. Bottom: Schematics of the VSC enhanced reaction mechanism, which we consider four vibrational diabatic states \(\{\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle ,\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}}\right\rangle ,\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle ,\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}}^{{\prime} }\right\rangle \}\) (see “Method”, Eqs. (38) and (39)). a Cavity mode promotes the transition \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\), leading to the rate constant enhancement36. b Considering the photon-dressed vibrational states \(\{\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle ,\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle ,\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle \}\) (as well as the corresponding states for the right well), the cavity-loss environment promotes the photonic excitation \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle\), and then the photonic excitation is converted into vibrational excitation through \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\), being an additional channel provided by coupling to the cavity. The phonon bath still enables the mechanism under panel (a).
In this work, we present a complete mechanistic picture to understand a single molecule strongly coupled to a cavity and how VSC enhances the rate constant. In particular, we investigate how cavity lifetime τc influences the rate constants and derive a new analytic expression of the VSC rate constant under the lossless regime, based on a mechanistic observation that the rate-limiting step is the photonic excitation and the subsequent excitation transfer between photonic and vibrational DOFs. The resulting analytic rate theory, denoted as \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (see Eq. (17)), successfully described the VSC rate constant in the lossless regime and is in excellent agreement with the numerically exact results. Not only it predicts the correct resonance behavior at ωc = ω0, but also gives a clear explanation for the intimate connection between the VSC-modified rate constant and the optical lineshape \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) (Eq. (14)). To the best of our knowledge, this is the first analytic theory that explains the close connection between rate constant changes and lineshape of the vibrations.
Under the resonance condition (Eq. (4)), \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) is proportional to \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) in the lossless regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)), whereas kVSC (Eq. (2)) is proportional to τc in the lossy regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)). Moreover, we proposed an interpolated rate expression between kVSC and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) to describe the crossover phenomenon for intermediate τc, and predicted that the maximal enhancement will be reached at \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\). These analytic expressions provide a complete description for the τc turnover behavior of the VSC rate constant. Particularly, it provides a novel understanding of the physical role of cavity lifetime in VSC-modified chemical dynamics, that \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) can be viewed as a friction parameter based on the Kramers theory38,39. Under the low friction regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}\)), the reaction rate is limited by photonic excitation (which resembles energy diffusion) and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\propto {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\), while under the high friction regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}\)), the reaction rate is limited by light–matter conversion (which resembles spatial diffusion), and \({k}_{{{{{{{{\rm{VSC}}}}}}}}}\propto 1/({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1})\). Further, we discussed the temperature dependence of the VSC-modified rate constants and derived expressions of the effective change in activation enthalpy and entropy4, which also agree well with the numerical exact simulations. Finally, we discussed the resonance condition at the normal incidence for a Fabry–Pérot (FP) cavity with one or two-dimensional in-plane momenta31.
Results and discussions
Theoretical model
The molecule-cavity Hamiltonian is expressed as
where \({\hat{H}}_{{{{{{{{\rm{M}}}}}}}}}\) is the molecular Hamiltonian, \({\hat{H}}_{\nu }\) describes the phonon coupling to the molecular reaction coordinate, \({\hat{H}}_{{{{{{{{\rm{LM}}}}}}}}}\) describes the light–matter coupling (cavity-molecule interactions), and \({\hat{H}}_{{{{{{{{\rm{c}}}}}}}}}\) describes the cavity loss bath. In particular, \({\hat{H}}_{{{{{{{{\rm{M}}}}}}}}}=\frac{{\hat{P}}^{2}}{2M}+V(\hat{R})\), where M is the effective mass of the nuclear vibration, \(V(\hat{R})\) is the ground electronic state potential energy surface modeled as a double-well potential (see “Methods”, Eq. (37) for details), and \(\hat{R}\) is the reaction coordinate. The light–matter interaction term is expressed as16,35,36,40
where \({\hat{q}}_{{{{{{{{\rm{c}}}}}}}}}=\sqrt{\hslash /(2{\omega }_{{{{{{{{\rm{c}}}}}}}}})}(\hat{a}+{\hat{a}}^{{{{\dagger}}} })\) and \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}=i\sqrt{\hslash {\omega }_{{{{{{{{\rm{c}}}}}}}}}/2}({\hat{a}}^{{{{\dagger}}} }-\hat{a})\) are the photon mode coordinate and momentum operators, respectively, where \({\hat{a}}^{{{{\dagger}}} }\) and \(\hat{a}\) are the creation and annihilation operators for a cavity mode, and ωc is the cavity mode frequency. Further, the single molecule, single mode light–matter coupling strength is35,36
where ϵ0 is the permittivity inside the cavity, and \({{{{{{{\mathcal{V}}}}}}}}\) is the effective quantization volume of that mode. In Eq. (6), we had explicitly assumed that the ground state dipole moment \(\mu (\hat{R})\) is linear and always aligned with the cavity polarization direction27,35, such that \(\mu (\hat{R})=\hat{R}\). Based on the two diabatic states \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle\) and \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) in the left well (see Eqs. (38) and (39) in “Method”), we define the quantum vibration frequency of the reactant as \({\omega }_{0}\equiv {{{{{{{{\mathcal{E}}}}}}}}}^{{\prime} }-{{{{{{{\mathcal{E}}}}}}}}=1172.2\,{{{{{{{{\rm{cm}}}}}}}}}^{-1}\), which is directly related to the quantum transition of \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) and can be determined by spectroscopy measurements (IR or transmission spectra). The Rabi splitting from the spectral measurements is related to the light–matter coupling strength as follows
where the transition dipole matrix element is defined as \({\mu }_{{{{{{{{{\rm{LL}}}}}}}}}^{{\prime} }}=\langle {\nu }_{{{{{{{{\rm{L}}}}}}}}}| \hat{R}| \nu {{\prime} }_{{{{{{{{\rm{L}}}}}}}}}\rangle\). See “Methods”, Eqs. (41) and (42) for a detailed description of the other terms in the VSC Hamiltonian. In this work, we will use ηc in Eq. (7) and ΩR in Eq. (8) as interchangeable phrases.
A schematic illustration of the model system is provided in the top panel of Fig. 1. Figure 1a–b presents the potential V(R) for the ground state along the reaction coordinate R, as well as key quantum states associated with the two different mechanisms of the VSC-modified kinetics. Specifically, Fig. 1a shows the four diabatic matter states \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle\) (blue), \(\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}}\right\rangle\) (orange), \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) (red), \(\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}}^{{\prime} }\right\rangle\) (green), in which the cavity is included in the bath and described by an effective spectral density Jeff(ω) (see Supplementary Note 2, Section A). The major VSC enhanced reaction channel is shown in Eq. (1), in which k1 is the rate-limiting step. This mechanism is confirmed for the lossy regime using the exact quantum dynamics simulations in our previous work36,37. Figure 1b shows several key photon-dressed vibration states. These states include \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle\) (blue), \(\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}},0\right\rangle\) (orange), \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle\) (magenta), \(\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}},1\right\rangle\) (green-yellow), \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) (red), \(\left\vert {\nu }_{{{{{{{{\rm{R}}}}}}}}}^{{\prime} },0\right\rangle\) (green) for both the reaction coordinate \(\hat{R}\) and the cavity mode \({\hat{q}}_{{{{{{{{\rm{c}}}}}}}}}\), in which the cavity is included in the system and coupled to the photon-loss environment characterized by the spectral density Jc(ω) (see Supplementary Note 2, Section B). The VSC-enhanced reaction channel is shown later in Eq. (11), in which the photonic excitation \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle\) and the conversion to vibrational excitation \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) are sequential steps which together act as the rate-limiting steps. Later, we will see that the FGR rate theory constructed using Eq. (1) works for the lossy regime while using Eq. (11) works for the lossless regime.
FGR rate theory in the lossy regime
For the lossy regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}\)), the VSC modified rate constant is expressed in Eq. (2) based on our recent work36, which sharply peaks at ωc = ω0. Under the resonance condition (ωc = ω0), Eq. (2) reduces to
suggesting that a larger enhancement of the rate constant will be reached with a longer τc. Eq. (2) provides an excellent agreement with HEOM under this lossy regime, as is verified in the previous work36. When τc further increases, Eq. (2) needs to include phonon broadening effect36 to avoid divergence when τc → ∞, resulting in
which is a convolution between Eq. (2) and the broadening function \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) (see Eq. (14)), and the fundamental scaling suggested in Eq. (9) is preserved.
Figure 2a presents the results of k/k0 using both the numerically exact HEOM simulations (open circles with thin guiding lines) and the analytic FGR rate theory (thick solid curves), with the light–matter coupling strength ηc = 0.05 a.u. For the analytic FGR rate theory, we present the results k/k0 = 1 + 0.5kVSC/k0, where kVSC is evaluated using Eq. (10) and k0 is directly obtained from HEOM simulations, and an empirical re-scaling factor 0.5 is applied (see “Method”, rate constant calculations). One can see that Eq. (10) provides an excellent agreement with the HEOM results when τc < 100 fs. Both the resonance peak position and the width of the rate constant modifications are well captured.
Comparisons are made between the numerically exact HEOM results (open circles with thin guiding lines) and the FGR rate constants (both kVSC and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\)) which are re-scaled by a factor of 0.5 (solid lines). The light–matter coupling strength is fixed at ηc = 0.05 a.u. a Resonance peaks of k/k0 for VSC effect under the lossy regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)). The FGR rates using kVSC in Eq. (10) (thick solid lines) are compared to the HEOM results (open circles with thin guiding lines) under a variety of τc values. b The values of k/k0 under the resonance condition ωc = ω0 as a function of τc. The results of HEOM (blue open circles), FGR rates using kVSC in Eq. (10) (red solid line), FGR rates using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) (blue solid line), and FGR rates using \({k}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{int}}}}}}}}}\) in Eq. (20) (gold dashed line) are presented. c Resonance peaks of k/k0 for VSC effect under the lossless regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)). The FGR rates using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) (thick solid lines) are compared to the HEOM results (open circles with thin guiding lines) under a variety of τc values.
Figure 2b presents the τc-dependence of k/k0 under the resonance condition (ωc = ω0), with ηc = 0.05 a.u., corresponding to a Rabi splitting of ΩR ≈ 25.09 cm−1 (based on Eq. (8)) or equivalently, the time scale of Rabi oscillation \({\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\approx 211.6\) fs. The numerically exact HEOM results (blue open circles) show a turnover behavior on k/k0 when increasing τc from the lossy limit to the lossless limit. One can observe that the FGR curve using kVSC (Eq. (10), red) agrees well with the left-hand side of the HEOM turnover curve, corresponding to the lossy regime where τc < 100 fs. This is because when the cavity is lossy (with a small τc), the cavity mode thermalizes fast with the photon-loss bath, and τc serves as a broadening parameter in the effective spectral density36. The fundamental mechanism of the rate constant enhancement is the vibrational excitation \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) under the influence of the effective bath (see schematic in Fig. 1a).
However, Eq. (9) cannot described the VSC kinetics when further increasing τc so that the lossy regime \({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\) is no longer satisfied. This is because as τc increases, the photon-loss bath \({\hat{H}}_{{{{{{{{\rm{c}}}}}}}}}\) no longer plays the simple role of (homogeneous) broadening, breaking the fundamental mechanistic assumption in Eq. (1). A new analytic theory for this lossless regime is needed.
FGR rate theory in the lossless regime
When the cavity is under the lossless regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \, \gg \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)), the rate-limiting step of the reaction becomes the photonic excitation \(\left\vert 0\right\rangle \to \left\vert 1\right\rangle\) and the subsequent excitation energy transfer (see Fig. 1b). The VSC enhancement thus originates from the enhancement of the photonic excitation caused by the photon-loss bath \({\hat{H}}_{{{{{{{{\rm{c}}}}}}}}}\), as proposed in Ref. 35. Under this regime, the numerically exact HEOM simulations suggest the following reaction mechanism (schematically depicted in Fig. 1b)
and \({\tilde{k}}_{1},{\tilde{k}}_{2} \, \ll \, {\tilde{k}}_{3},{\tilde{k}}_{4}\). Note that the phonon bath \({\hat{H}}_{\nu }\) can still promote the transition \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\), and Eq. (1) is still one of the main mechanism for the reaction, either outside or inside the cavity.
According to FGR (with the system-bath partition described in Supplementary Note 2, Section B), the photonic excitation \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle\) rate constant \({\tilde{k}}_{1}\) can be evaluated using FGR, resulting in
where n(ω) is the Bose–Einstein distribution in Eq. (3). Details of the derivation are provided in Supplementary Note 5, section A. Note that there is no resonance behavior in \({\tilde{k}}_{1}\), and it becomes unbounded when τc → 0. The resonance behavior and boundedness of the rate constant will be ensured by \({\tilde{k}}_{2}\) associated with the \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) transition, which can be evaluated as
Details of the derivation are provided in Supplementary Note 5, Section B. Due to the molecular phonon bath \({\hat{H}}_{\nu }\), one needs to further consider the broadening effect in the vibration frequency ω0, described by a lineshape function \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }({\omega }_{{{{{{{{\rm{c}}}}}}}}}-{\omega }_{0})\). Under the homogeneous limit, \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }({\omega }_{{{{{{{{\rm{c}}}}}}}}}-{\omega }_{0})\) has a Lorentzian form as follows41
with the broadening parameter36,42
where \({\epsilon }_{z}\equiv \langle \nu {{\prime} }_{{{{{{{{\rm{L}}}}}}}}}| \hat{R}| \nu {{\prime} }_{{{{{{{{\rm{L}}}}}}}}}\rangle -\langle {\nu }_{{{{{{{{\rm{L}}}}}}}}}| \hat{R}| {\nu }_{{{{{{{{\rm{L}}}}}}}}}\rangle\). Note that \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) in Eq. (14) is also an approximate IR spectra function under the homogeneous broadening limit (see ref. 41, Eq. (6.67)), with the width Γν. The parameters used in this study give Γν ≈ 30.83 cm−1, which is in line with the typical values of the molecular systems investigated in the recent VSC experiments1,10. As such, the rate constant \({\tilde{k}}_{2}\) can be evaluated as convolution between \({\tilde{\kappa }}_{2}\) (Eq. (13)) and \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) (Eq. (14)) as
Further, the population dynamics from HEOM (see Supplementary Fig. 2) suggests that \({\tilde{k}}_{1}\) and \({\tilde{k}}_{2}\) steps can be regarded as sequential kinetic steps, and the populations of \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle\) and \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) both reach to a steady state behavior (plateau in time). Making the steady-state approximation for the mediating state, the overall rate constant for the \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) steps is expressed as follows
which contains both the resonance structure (due to the line shape function \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }({\omega }_{{{{{{{{\rm{c}}}}}}}}}-{\omega }_{0})\)) and the boundedness with respect to τc. Because that \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) is rate-limiting for the entire reaction process in Eq. (11), the VSC-modified rate constant can also be evaluated as \(k={k}_{0}+{\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) under the lossless regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}\)), being valid under the FGR limit43,44. Similar to the lossy regime, we report
where k0 is the outside cavity rate constant, and α is an ad hoc rescaling factor due to the inaccuracy of the FGR level of theory. Practically, we found α = 0.5 will match the numerically exact results from HEOM45.
Eq. (17) is the first main theoretical result in this work. This analytic theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (as well as in Eq. (10) for kVSC) implies that the optical lineshape of the molecule described by \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) is intimately connected to the VSC kinetics modifications, due to the fact that both are sensitive to the vibrational quantum transition. The current theory in Eq. (17) provides an analytic answer to the early numerical observations35,36 from HEOM simulations. Under the resonance condition (ωc = ω0), Eq. (17) becomes
which implies \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) increases as τc decreases, being opposed to Eq. (9) (under the lossy regime). When the cavity approaches the lossless regime (τc → ∞), \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\to 0\) so that there will be no cavity modifications.
One can observe in Fig. 2b that the \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) curve (Eq. (19), blue) agrees well with the right-hand side of the HEOM turnover curve, corresponding to the lossless regime where τc > 500fs, although a re-scaling factor of 0.5 is multiplied to \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\). The τc → ∞ limit has been numerically investigated in Ref. 35, suggesting that k/k0 increases as τc decreases. The τc → 0 limit has been numerically checked in ref. 36, suggesting that k/k0 increases as τc increases. Combining the knowledge of Eq. (9) and Eq. (19), we can predict that there will be a turnover behavior for the VSC-modified rate constant. Equivalently speaking, when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\to 0\) (small friction limit), \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\propto {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\), and when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\to \infty\) (large friction limit) kVSC ∝ τc. The scaling of the VSC rate constant as a function of \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) coincides with the well-known Kramers turnover38,39. As such, one can regard \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) as the friction parameter for the photon-loss environment. A similar crossover phenomenon has also been discovered in spin relaxation kinetics in semiconductors, e.g., the D’yakonov–Perel’ mechanism under different momentum scattering rates46,47,48,49,50,51.
Figure 2c presents the ωc-dependence of k/k0 from the numerically exact HEOM results (open circles with thin guiding lines), and the FGR rate constant using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) (thick solid lines). One can see that \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) agrees well with the exact results for τc > 500 fs, and the resonance peak positions are well captured by FGR (with a re-scaling factor of 0.5 applied). In addition, the widths given by \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) are in agreement with the HEOM results for a wide range of τc. We also note that the long tails towards lower cavity frequencies in the FGR results disagree with the HEOM results, due to the Lorentzian lineshape function decaying slowly while n(ωc) increases fast when decreasing ωc.
VSC-modified rate constant and the optical lineshape
Apart from predicting the correct resonance condition (ωc = ω0), \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) also predicts that the width of the rate constant profile is determined by the lineshape function of the molecular vibration spectra \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }({\omega }_{{{{{{{{\rm{c}}}}}}}}}-{\omega }_{0})\), with width Γν (see Eq. (15)). Note that \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) is slightly broader than \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) due to the Bose–Einstein distribution function n(ωc) (see Eq. (3)). Figure 3a presents k/k0 obtained by HEOM simulations (light blue open circle and shaded area) and FGR from Eq. (17) (dark blue solid line), respectively, as well as the IR spectra of the bare molecule system obtained from HEOM simulation (red solid line with shaded area). The rate profile is the same as the magenta curve in Fig. 2c, where ηc = 0.05 a.u. and τc = 1000 fs. The IR spectra are simulated by HEOM, with details presented in Supplementary Note 6. The optical spectra can be well approximated as \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) in Eq. (14) (red open circles), which is visually identical to the HEOM results. The similar trend of the vibration spectra for the molecular system outside the cavity and the VSC-modified rate constant profile are a ubiquitous feature for most of the VSC experiments so far1,5,10,14, with the peaks both located at ωc = ω0 and the widths roughly at Γν (although there are counter-examples, such as Fig. 3a of ref. 2). This feature is observed in current numerical simulations, as well as in the previous work35, which can be explained by the \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) expression in Eq. (17).
a The rate profile k/k0 obtained from HEOM simulations (blue open circles) and the FGR expression using Eq. (17) (blue thick line), as well as the IR spectra of the bare molecule system from HEOM (thick solid line) and using Eq. (14) (open circles). The rate profile is the same as the violet curve in Fig. 2c. b Cavity lifetime τc-dependence of the VSC rate constant k/k0 under various ΩR obtained from HEOM simulations (open circles with thin guiding line) as well as the interpolated expression in Eq. (20) (solid lines), and the cavity frequency is fixed at the resonance condition ωc = ω0. The dashed vertical lines denote the position where \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\). c Relation between k/k0 at resonance (ωc = ω0) and the Rabi splitting ΩR, with results obtained from HEOM (red circles) and FGR (red solid line) using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (19). The change of the effective free energy barrier height Δ(ΔG‡) is also presented, with HEOM (blue circles) and the FGR (blue solid line) using Eq. (22).
FGR rate theory in the intermediate regime
Under the intermediate regime (\({\tau }_{{{{{{{{\rm{c}}}}}}}}} \sim {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\)), it is difficult to have a simple reaction mechanism and derive an analytical rate constant expression. This is indeed the case for Kramers turnover when the friction parameter is in between the energy and spatial diffusion limits38. A similar situation also occurs for the theory of electron transfer under the non-adiabatic limit (golden rule, Marcus Theory) or adiabatic limit (Born–Oppenheimer, Hush Theory), where well-defined rate theories are available in both regimes52,53,54,55, but there is no analytic theory for the entire crossover region. Nevertheless, one can apply an ad hoc approach by interpolating the two FGR expressions in Eqs. (2) and (17) as follows53,55
which is the second main theoretical result in this work. The numerical result of FGR rates using \({k}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{int}}}}}}}}}\) in Eq. (20) is presented in Fig. 2b (golden dashed line), with a re-scaling factor of 0.5 applied to both kVSC (Eq. (10)) and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)). One can see that Eq. (20) correctly captured the turnover behavior in the τc-dependence of VSC rate constant, which maximizes at around τc = 200 fs and agrees with the HEOM simulations, although being less accurate than either Eq. (2) in the lossy regime or Eq. (17) in the lossless regime. As a corollary of \({k}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{int}}}}}}}}}\), the maximum enhancement of the VSC rate constant can be reached when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\). This is because under the resonance condition ωc = ω0, Eq. (20) becomes (c.f. Eqs. (9) and (19))
where the equal sign is satisfied under \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\).
Figure 3b presents the τc-dependence of VSC rate constants under different Rabi splittings ΩR, obtained from the numerically exact HEOM simulations (open circles with thin guiding line) as well as the interpolated expression in Eq. (20) (solid lines). All pairs of curves show a similar turnover behavior along τc but differ in the peak positions. The dashed vertical lines denote the position where \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\) at the corresponding ΩR value, which coincides with the peak positions of the turnover curves. As a result, the expression of \({k}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{int}}}}}}}}}\) predicts that the maximum enhancement of VSC rate constants is reached when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\), in agreement with the numerically exact simulations.
Effect of the Rabi splitting
We further explore the effect of the light–matter coupling strength on the VSC rate constant and the accuracy of the FGR expression in Eq. (19) (Eq. (17) under the resonance condition) in the lossless regime. By doing so, we fix the cavity lifetime as τc = 1000 fs. Figure 3c presents the relation between k/k0 at resonance (ωc = ω0) under various Rabi splitting ΩR, obtained from the HEOM simulations (red circles) and the FGR expression (red solid line) using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (19) with a re-scaling factor of 0.5 on \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\). Over up to 100 cm−1 Rabi splitting, the FGR expression (Eq. (19)) correctly captures the ΩR-dependence that first scales as \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\propto {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{2}\), then plateau (saturated). This is because when ΩR becomes large, only \({\tilde{k}}_{1}\) (Eq. (12)) is rate limiting, which is ΩR-independent.
Figure 3c further presents the change of the effective free energy barrier Δ(ΔG‡), directly calculated from the rate constant ratio k/k0 obtained from HEOM simulations. To account for the “effective change” of the Gibbs free energy barrier Δ(ΔG‡) as follows4,11,36
Note that this is not an actual change in the free-energy barrier, but rather an effective measure of the purely kinetic effect. Here, one can see a non-linear relation of Δ(ΔG‡) with ΩR that has been observed experimentally6, and the theory in Eq. (19) provides a semi-quantitative agreement with the numerically exact results from HEOM simulations.
Temperature dependence of the VSC rate constant
Experimentally, it was found that VSC induces changes in both effective activation enthalpy and activation entropy when using the Eyring equation to interpret the change of the rate constant1,10,11, which remains to be theoretically explained. We emphasize that based on our current theory, the VSC modification mechanism is not due to the direct modification of the Entropy or Enthalpy, but rather through the mechanisms summarized in Eq. (11) (for the lossless regime) and Eq. (1) (for the lossy regime). However, if one chooses to interpret the change of the rate constant through these enthalpy and entropy changes, then the current theory in Eq. (17) can indeed explain both changes. Using the Eyring equation, the temperature dependence of the reaction rate constant is
where ΔH‡ and ΔS‡ are the effective activation enthalpy and entropy, respectively, which can be extracted by plotting \(\ln (k/T)\) as a function of 1/T. We further denote the effective activation enthalpy and entropy inside the cavity as \(\Delta {H}_{{{{{{{{\rm{c}}}}}}}}}^{{{{\ddagger}}} }\) and \(\Delta {S}_{{{{{{{{\rm{c}}}}}}}}}^{{{{\ddagger}}} }\), respectively, and the corresponding values outside the cavity as \(\Delta {H}_{0}^{{{{\ddagger}}} }\), \(\Delta {S}_{0}^{{{{\ddagger}}} }\), respectively. One can further define their difference as \(\Delta \Delta {H}^{{{{\ddagger}}} }\equiv \Delta {H}_{{{{{{{{\rm{c}}}}}}}}}^{{{{\ddagger}}} }-\Delta {H}_{{{{{{{{\rm{0}}}}}}}}}^{{{{\ddagger}}} }\), and \(\Delta \Delta {S}^{{{{\ddagger}}} }\equiv \Delta {S}_{{{{{{{{\rm{c}}}}}}}}}^{{{{\ddagger}}} }-\Delta {S}_{{{{{{{{\rm{0}}}}}}}}}^{{{{\ddagger}}} }\), which characterizes the pure cavity induced effects. According to the assumption that k = k0 + kVSC, they can be evaluated analytically as follows
where the detailed derivations are provided in Supplementary Note 7. Eq. 24a-b can be evaluated by using HEOM results, or the FGR expressions, either kVSC in Eq. (2) (or Eq. (10) to be more accurate) for the lossy case or \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) for the lossless case. The previous work based on the classical Grote–Hynes rate theory15 can only explain the change in ΔΔS‡. The current FGR-based theory can explain changes in both ΔΔH‡ and ΔΔS‡, which has been observed in experiments4,6.
Figure 4a presents the temperature dependence of the VSC rate constant, plotting as \(\ln (k/{k}_{0})\) as a function of 1/T. The cavity lifetime is fixed as τc = 1000 fs, and the cavity frequency is ωc = ω0. Figure 4a shows the Eyring-type plots for reactions outside the cavity (black points) and inside a resonant cavity under various light–matter coupling strengths. The rate constants were obtained from HEOM simulations (dots), and fitted by the least square to obtain linearity (thin lines). One can see that as ΩR increases, the slope of the Eyring plots becomes more negative (an increasing the effective activation enthalpy). Meanwhile, the effective entropy also increased significantly as one increase ΩR. The current theory explains both changes of ΔΔH‡ and ΔΔS‡, and the temperature-dependence in Fig. 4a has been experimentally observed (e.g., Fig. 4 in ref. 56).
The cavity lifetime τc is fixed at 1000 fs, and the cavity frequency is kept at the resonance condition ωc = ω0. a Eyring-type plots for \(\ln (k/{k}_{0})\) as a function of 1/T, for reaction outside the cavity (black points) and inside the resonant cavity under various light–matter coupling strengths. b Effective activation enthalpy under different ΩR values, with the results obtained from the exact HEOM simulations (blue open circles) and the FGR results (gold dashed line) using Eq. (17) (where the value of \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) is re-scaled by a factor of 0.5). c Effective activation entropy under different ΩR values obtained from the exact HEOM simulations (blue open circles) and the FGR results (gold dashed line) using Eq. (17) (where the value of \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) is re-scaled by a factor of 0.5).
Figure 4b presents the change of the effective activation enthalpy ΔΔH‡ as increasing ΩR. The HEOM results for ΔΔH‡ (blue open circles with thin guiding lines) are extracted from the slopes of the fitted lines in Fig. 4a. Further, the FGR results (gold dashed line) are presented, in which kVSC is calculated using Eq. (17) (re-scale by a factor of α = 0.5) and plug-in Eq. (24a) to obtain the cavity induced change ΔΔH‡. When kVSC is small, Eq. (24a) is proportional to kVSC, i.e., proportional to \({\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{2}\) according to the analytic FGR rate theory (see Eq. (17)). One can see that from Fig. 4b when ΩR < 15 cm−1, \(\Delta {H}_{{{{{{{{\rm{c}}}}}}}}}^{{{{\ddagger}}} }\) increases quadratically with ΩR, and the FGR results agree with the HEOM results. When ΩR > 15 cm−1, the behavior deviates from quadratic scaling, and FGR results still closely match the trend of HEOM results. Figure 4c presents the change of the effective activation entropy ΔΔS‡, with results obtained from HEOM (blue open circles with thin line) and FGR (golden dashed line), where the FGR also provides a good agreement with the exact results. Note that Eq. 24a-b also works well in the lossy regime, where the results with τc = 100 fs and k/k0 evaluated using Eq. (10) are presented in Supplementary Fig. 3.
Resonance condition at the normal incidence
The dispersion relation of a Fabry–Pérot (FP) microcavity6,16,57 is
where c is the speed of light in vacuum, nc is the refractive index inside the cavity, c/nc is the speed of the light inside the cavity, and θ is the incident angle, which is the angle of the photonic mode wavevector k relative to the norm direction of the mirrors. For simplicity, we explicitly drop nc throughout this paper (because of the experimental value nc ≈ 1). The many-mode Hamiltonian is provided in Supplementary Note 8. When k∥ = 0 (or θ = 0), the photon frequency is
which is the cavity frequency we introduced in the previous discussions (Eq. (4)). Experimentally, it is observed that only when ωc = ω0 (known as the normal incidence condition) will there be VSC effects2,4,6,10,31. For a red-detuned cavity (ωc < ω0), there are still a finite number of modes (with a finite value of k∥), such that ωk = ω0. This is referred to as the oblique incidence, but there is no observed VSC effect even though polariton states are formed1,6,31. As mentioned in ref. 2, “Tuning the cavity so that VSC occurs at normal incidence is essential to observe the modification of chemical properties. In this condition, the system is at the minimum energy in the polaritonic state2”. Despite recent theoretical progress58,59, there is no accepted theoretical explanation for VSC effect only observed at the normal incidence, although intuitively, the group velocity ∂ωk/∂k∥ = 0 at k∥ = 0 and make that point special, as hinted by Ebbesen and co-workers2. Our recent work suggests that for the analytic expression kVSC (Eq. (2)), it is possible to explain such a normal incidence effect when considering many cavity modes45. In this work, we theoretically explore such normal incidence conditions for the new analytic expression \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) under the lossless regime.
For k∥ > 0, the mode has a finite momentum in the in-plane direction. Because of this in-plane propagation, the photon leaving the effective mode area is characterized by the following effective lifetime45
where \({{{{{{{\mathcal{D}}}}}}}}\) characterizes the spatial extent of a given mode (along the k∥ direction). Using the experimental molecular density and the effective number of molecules coupled to a given mode, one can estimate \({{{{{{{\mathcal{D}}}}}}}} \, \approx \, 1{0}^{-1} \sim 100\,\mu{{{{{\rm{m}}}}}}\), with details provided in Supplementary Note 10, section A. We want to emphasize that τ∥ differs from the cavity lifetime τc which considers the photon loss in the k⊥ direction due to leaking outside the cavity. As a result of τ∥, the thermal photon number should be modified as45n(ωk) → neff(ωk) with the following expression
due to the detailed balance relation.
Using the same procedure of the FGR derivation (as used for Eq. (17)), the VSC enhanced rate constant under the lossless regime is
where \({g}_{{{{{{{{\rm{c}}}}}}}}}={\mu }_{{{{{{{{{\rm{LL}}}}}}}}}^{{\prime} }}\sqrt{1/(2\hslash {\epsilon }_{0}{{{{{{{\mathcal{V}}}}}}}})}\) is the Jaynes–Cummings60 type light–matter coupling strength that does not depend on ωk. Note that in the literature, \({\Omega }_{{{{{{{{\rm{R}}}}}}}}}=4{g}_{{{{{{{{\rm{c}}}}}}}}}^{2}{\omega }_{{{{{{{{\rm{c}}}}}}}}}\) for the resonance condition. When there is only one mode, Eq. (29) reduces back to Eq. (17). Further, ϕk describes the angle between the molecular dipole and the kth cavity mode. For the 1D FP cavity (one dimensional for the k∥ direction), \(\cos {\phi }_{{{{{{{{\bf{k}}}}}}}}}=1\). For the 2D FP cavity (two dimensional for the k∥ direction), we assume an isotropic average \({\cos }^{2}{\phi }_{{{{{{{{\bf{k}}}}}}}}}\to \langle {\cos }^{2}{\phi }_{{{{{{{{\bf{k}}}}}}}}}\rangle =1/2\). As such, the rate constant in Eq. (29) can be evaluated by replacing the summation with an integral as follows
where gD(ω) is the DOS for the cavity modes. Using the cavity dispersion relation in Eq. (25), the photonic density of states (DOS) for a 1D FP cavity is expressed as follows45,
where Θ(ω − ωc) is the Heaviside step function, Δk∥ is the spacing of the in-plane wavevector k∥ (or the k-space lattice constant). Note that g1D(ω) has a singularity at ω = ωc, which is known as (the first type of) the van-Hove-type singularity61. The DOS for a 2D FP cavity is expressed as45
which does not have any singularity.
For a 1D FP cavity, using g1D(ω) in Eq. (31) and evaluating the integral in Eq. (30) (see details in Supplementary Note 9) results in
which is identical to Eq. (17) (with \({\Omega }_{{{{{{{{\rm{R}}}}}}}}}=4{g}_{{{{{{{{\rm{c}}}}}}}}}^{2}{\omega }_{{{{{{{{\rm{c}}}}}}}}}\)), with an additional \({{{{{{{\mathcal{M}}}}}}}}=\int\,{g}_{{{{{{{{\rm{1D}}}}}}}}}(\omega )d\omega\) which is the number of cavity modes. Thus, for a 1D FP cavity, the peak of the expression in Eq. (33) is located at ωc = ω0 where k∥ = 0, due to the presence of the van-Hove singularity. This means that VSC modification occurs only when ωc = ω0 for a 1D FP cavity. We have also numerically evaluated Eq. (30) and compared it with Eq. (33) for the VSC-modified rate constant, presented in Supplementary Fig. 4, which shows a nearly identical behavior.
On the other hand, all of the known VSC experiments1,6,10,31 have been performed in 2D FP cavities. For a 2D FP cavity, using g2D(ω) in Eq. (32) to evaluate Eq. (29), the VSC rate constant becomes
where \({{{{{{{\mathcal{C}}}}}}}}=2{{{{{{{\mathcal{M}}}}}}}}/({\omega }_{{{{{{{{\rm{m}}}}}}}}}^{2}-{\omega }_{{{{{{{{\rm{c}}}}}}}}}^{2})\), \({{{{{{{\mathcal{M}}}}}}}}=\int\,{g}_{{{{{{{{\rm{2D}}}}}}}}}(\omega )d\omega\) is the number of modes, ωm is the integration cutoff frequency (which is treated as a convergence parameter), and \({\tau }_{\parallel }(\omega )=({{{{{{{\mathcal{D}}}}}}}}/c)\cdot \omega /\sqrt{{\omega }^{2}-{\omega }_{{{{{{{{\rm{c}}}}}}}}}^{2}}\) (c.f. Eq. (27)). See Supplementary Note 9 for detailed derivations. As a crude estimation, one can approximate \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0}) \, \approx \, \delta (\omega -{\omega }_{0})\), such that the integral in Eq. (34) can be evaluated analytically, leading to
Since usually \(c{\tau }_{{{{{{{{\rm{c}}}}}}}}}/{{{{{{{\mathcal{D}}}}}}}} \, \gg \, 1\), Eq. (35) has a sharp maximum value at ωc = ω0 and tails toward the ωc < ω0 side.
Figure 5 presents the VSC-enhanced rate constant using the FGR expression under different Rabi splitting ΩR values inside (a) a 1D FP cavity and (b) a 2D FP cavity, where the cavity lifetime is τc = 1000 fs. Figure 5a presents \(k/{k}_{0}=1+0.5\,{\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{1D}}}}}}}}}/{{{{{{{\mathcal{M}}}}}}}}{k}_{0}\), where the number of modes \({{{{{{{\mathcal{M}}}}}}}}\) has been divided to present a normalized result. This is identical to the single-mode expression (Eq. (17)) due to the van-Hove-type singularity in the 1D DOS (see Eq. (31)). Figure 5b presents \(k/{k}_{0}=1+0.5\,{\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}/{k}_{0}\) value for a single molecule coupled to many modes inside a 2D FP cavity, where \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) was evaluated by performing direct sum using Eq. (29) (solid lines), as well as by using \({k}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) expression in Eq. (34) (open circles), which are identical to each other. Note that both \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{1D}}}}}}}}}\) and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) are re-scaled by a factor of 0.5 to be consistent with Fig. 2. Here, we choose \({{{{{{{\mathcal{D}}}}}}}}=1\,\mu{{{{{\rm{m}}}}}}\) for the effective mode diameter, the effective cavity size \({{{{{{{\mathcal{L}}}}}}}}=1\) mm (probing area) to discretize the 2D cavity dispersion relation when using Eq. (29) (solid lines), with ωm = 5ωc which generates a total number of \({{{{{{{\mathcal{M}}}}}}}}\approx 1{0}^{6}\) modes for the 2D FP cavity. We use the same ωm value to perform integration using Eq. (34) (open circles). The details are provided in Supplementary Note 10, section B. One can observe that the resonance peak is still centered around ωc = ω0 but slightly red-shifted, demonstrating the normal incidence condition. The approximate analytic expression of \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) in Eq. (35) gives a similar long tail for ωc < ω0 but a much sharper decay for ωc ≥ ω0. Overall, the resonance peak is asymmetric as it tails toward the lower energy regions. Future VSC experiments are required to explore if there is any asymmetry in the rate constant profile.
FGR rate profiles of k/k0 as a function of ωc, where the cavity lifetime is τc = 1000 fs. Results under various light–matter coupling strengths are presented. a FGR rate using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{1D}}}}}}}}}\) (Eq. (33)) where the number of modes \({{{{{{{\mathcal{M}}}}}}}}\) is divided, which is identical to the single mode case in Eq. (17). b FGR rate profiles for many mode cases inside a 2D FP cavity, where the results obtained by performing direct sum using Eq. (29) (solid lines) and by performing integration using \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}^{{{{{{{{\rm{2D}}}}}}}}}\) in Eq. (34) (open circles) are presented.
Experimental connections
The current theory is valid for N = 1 or a few molecules strongly coupled to the cavity, such that the individual light–matter coupling ηc is strong. Experimentally, it is now possible to achieve strong (or even ultra-strong62) light–matter couplings between a plasmonic nanocavity and a few vibrational modes62,63, such that \({\Omega }_{{{{{{{{\rm{R}}}}}}}}} \, \gg \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) (for N = 1). In these experimental setups62,63, the current theory (\({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17)) can be directly applied, and all of the predictions could be verified experimentally, e.g., the τc behavior in Fig. 2 and various scaling relations in Fig. 3.
On the other hand, in all existing VSC experiments1,2,10,14, the Rabi splitting is achieved through a collective light–matter coupling between N vibrational modes with the cavity, such that Eq. (8) should be modified as16,31,64,65
It was estimated that N ≈ 106 ~ 1012 per effective cavity mode64, and ΩR,N ≈ 100 cm−1 for the typical VSC experiments4,10. The strong coupling condition in the experiments is achieved when \({\Omega }_{{{{{{{{\rm{R}}}}}}}},N} \, \gg \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) and the optical spectra of the molecule-cavity hybrid system have a peak splitting. However, the fundamental mechanism of the experimentally observed VSC effect (which happens under the collective coupling regime, Eq. (36)) remains to be explained.
If all molecules are perfectly aligned with the cavity field, the coupling strength per molecule ηc is bound to be very weak (\(\sim {\Omega }_{{{{{{{{\rm{R}}}}}}}},N}/\sqrt{N}\)). Recent theoretical work66 suggests that disorders of the molecular dipole distribution along the field polarization will create local strong coupling spots66, and in these “hot spots”, only a few molecules are strongly coupled to the cavity66 (which resembles a form of spin glass). If this is the case in the VSC experiments, then combining the \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) with the disorder-enhanced local coupling theory in Ref. 66 would likely explain the VSC enabled effect. On the other hand, the VSC-induced rate constant changes could originate from a non-trivial collective effect even though the individual ηc is tiny31. In this case, one has the scenario that \({\Omega }_{{{{{{{{\rm{R}}}}}}}}} \, \ll \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) (where ΩR ~ ηc) but \({\Omega }_{{{{{{{{\rm{R}}}}}}}},N} \, \gg \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) (due to the large N). As such, one would expect to use the kVSC (Eq. (2) or Eq. (10)) to describe the rate constant associated with a single molecule, add up all contributions in FGR and normalize it with 1/N (to avoid a simple concentration effect). This, however, will not give any significant change in the VSC-modified rate constant45, due to the large 1/N normalization factor. Future work needs to address this challenge, which might emerge from non-trivial collective effect due to non-local collective light–matter coupling67,68.
Nevertheless, our current theory suggests that measuring the τc-dependence of k/k0 could be the key to unraveling the fundamental mechanism in VSC. For example, under the strong coupling regime, if k/k0 decreases as τc increases, then the mechanism is likely to be \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) in Eq. (17) with the disorder-enhanced local coupling theory66. On the other hand, under the strong coupling condition \({\Omega }_{{{{{{{{\rm{R}}}}}}}},N} \, \gg \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\), if k/k0 increases as τc increases, then it implies that under the single molecule level ΩR ≪ τc, and the VSC mechanism is likely to be kVSC (Eq. (2) or Eq. (10)) with a collective mechanism yet to be discovered. Experimentally, the cavity lifetime (or the quality factor) for the distributed Bragg reflector (DBR) FP cavity can be modified by changing the number of coating layers69 or the curvature of the mirrors70. Other possible cavity structures that could achieve various Q factors are the “open” photonic structures71,72, which might be more suitable for polaritonic chemistry than planar cavities, as these mirror-free open structures generally support lower quality photonic modes than the standard FP cavity design. In either case, experimental measurements on the cavity lifetime dependence of the rate constant will provide invaluable insights into the nature of the VSC effects.
Further, going back to the experimental details, when comparing the theoretical results of k/k0 (cavity effect for inside and outside the cavity) to experiments, one will need to compare the results for two systems with different cavity lifetimes, and the outside cavity case could be the experimental set up of FP cavity with a τc → 0 limit (as our theoretical results suggested). This is because, in the real world, all planar wavelength scale structures support well-defined photonic modes. A final note is that many existing experiments compare reaction rate constants for molecules inside a cavity and outside a cavity (or on-resonance cavity and off-resonance cavity). If the on-resonance cavity sample has a different reaction rate to the non-cavity and/or off-resonance cavity sample, it is assumed that this change must be caused by strong coupling. This is a strong assumption and, if incorrect, could easily lead to false positives21,73. More careful experiment designs are needed in the future to differentiate between changes in reaction rate constant caused by polaritonic and non-polaritonic effects21,73. As pointed out by Thomas and Barnes74, it is also possible that cognitive bias could significantly influence the interpretation of strong coupling experiments and caution is needed to prevent false positive results.
Conclusion
We developed an analytic theory for the VSC-modified rate constant \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) for a single molecule strongly coupled to the cavity, under the lossless regime (when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1} \, \ll \, {\Omega }_{{{{{{{{\rm{R}}}}}}}}}\)). This analytic theory is based on the mechanistic observation of sequential rate-determining steps \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},0\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}},1\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} },0\right\rangle\) (outlined in Eq. (11)), which are observed in our numerically exact quantum dynamics simulations (see Supplementary Note 4). The theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) explains the resonance condition ωc = ω0 and the close connection between the rate constant modification \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) and the optical lineshape \({{{{{{{{\mathcal{A}}}}}}}}}_{\nu }(\omega -{\omega }_{0})\) (Eq. (14)). This explains why the VSC-modified rate distribution closely follows the optical spectra as observed in the VSC experiments1,2,10,14. This analytic theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) provides accurate ωc-dependence of the VSC rate constant enhancement compared to the numerically exact results from HEOM simulations.
The current analytic theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) also explains why under the lossless regime (\({\Omega }_{{{{{{{{\rm{R}}}}}}}}} \, \gg \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\)), the rate constant increase when decreasing the cavity lifetime τc (see Eq. (19)), agreeing with the previous numerically exact simulations35. Under the lossy regime (\({\Omega }_{{{{{{{{\rm{R}}}}}}}}} \, \ll \, {\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\)), our previous work36 provides an analytic theory kVSC (Eq. (2)), which predicts that the rate constant will increase as τc increases (see Eq. (9)). Both kVSC and \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) agree well with the numerical exact HEOM results under their specific regimes. The combination of \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) and kVSC (Eq. (2)) provides a complete picture of the τc-dependence of the VSC rate constant modification and suggests there should be a turnover behavior. The physical picture of the cavity enhancement effect for the rate constant is clarified by the reaction mechanisms in Eq. (1) (limited by vibrational excitation) under the lossy regime and Eq. (11) (limited by photonic excitation) under the lossless regime. The cavity loss parameter \({\tau }_{{{{{{{{\rm{c}}}}}}}}}^{-1}\) can thus be viewed as a friction parameter associated with the cavity mode \({\hat{q}}_{{{{{{{{\rm{c}}}}}}}}}\) and the turnover behavior of the rate constant is essentially the Kramers turnover. We also provided an interpolating scheme (Eq. (20)) for the description of the turnover phenomenon and predicted that the maximal enhancement will be reached when \({\tau }_{{{{{{{{\rm{c}}}}}}}}}={\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{-1}\) (see Eq. (21)), all agree well with the exact simulations.
The analytic theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) predicts that the VSC rate enhancement (Eq. (19)) scales as \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}/{k}_{0}\propto {\Omega }_{{{{{{{{\rm{R}}}}}}}}}^{2}\) as the light–matter coupling increases, then plateaus when ΩR becomes large. This is in excellent agreement with the numerically exact HEOM simulations and provides a non-linear relation between the change of the effective free energy barrier and the light–matter coupling strength (Fig. 3c), which has been observed in the VSC experiments4,6. The theory \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) (Eq. (17)) also predicts changes in both effective activation enthalpy and entropy (as observed in the experiments6), which agrees well with the numerical exact HEOM results within all the parameter regimes we explored. Although a re-scale parameter α = 0.5 is needed to bring the numerical values of the FGR rate constants in consistency with the HEOM exact results, the overall scaling relations with respect to ΩR, ωc, τc, and T reported in the paper are rather general and impressive, which should not be restricted to the detailed shape of the potential energy surface or environmental spectral density functions. We further generalized the \({\tilde{k}}_{{{{{{{{\rm{VSC}}}}}}}}}\) expression to consider the many mode effects, and the resulting theories (Eq. (33) for 1D FP cavity and Eq. (34) for 2D cavity) predict the normal-incidence resonance condition: the peak of the rate constant enhancement occurs when k∥ = 0 and ωc = ω0. Last but not least, our current theory also predicts that for two chemically similar reactions, if one satisfies k1 ≪ k2, k3 but the other does not (due to the low reaction barrier), then there will be a VSC effect for the first reaction but not for the second one. This is because for the second reaction, \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) is no longer rate limiting, and the cavity modification of this process will no longer influence the apparent rate constant. This might be the explanation for the recently observed null effects in VSC experiments22,23.
Despite the successes of the theory, it is limited to the situation of a single molecule strongly coupled to the cavity. In most of the experiments, a large collection of molecules (N = 106 ~ 1012) are collectively coupled to the cavity, and the coupling strength per molecule is rather weak. In the future, we aim to generalize the current analytic rate constant expression to explain the resonance suppression and the collective effect, to build a unified theory for the VSC-modified rate constant. Future efforts shall be focused on applying the current simulation approach and theory to realistic reaction systems with atomistic details26,75.
Methods
Model Hamiltonian
We use a double-well (DW) potential to model the ground state chemical reaction76,77
where M is chosen as the proton mass, ωb = 1000 cm−1 is the barrier frequency, and Eb = 2120 cm−1 is the barrier height. For the matter Hamiltonian \({\hat{H}}_{{{{{{{{\rm{M}}}}}}}}}=\hat{T}+\hat{V}\), the vibrational eigenstates \(\left\vert {\nu }_{i}\right\rangle\) and eigenenergies Ei are obtained by solving \({\hat{H}}_{{{{{{{{\rm{M}}}}}}}}}\left\vert {\nu }_{i}\right\rangle ={E}_{i}\left\vert {\nu }_{i}\right\rangle\) numerically using the discrete variable representation (sinc-DVR) basis78 with 1001 grid points in the range of [ − 2.0, 2.0]. To facilitate the mechanism analysis, we diabatize the two lowest eigenstates and obtain two energetically degenerate diabatic states
both with energies of \({{{{{{{\mathcal{E}}}}}}}}=({E}_{1}+{E}_{0})/2\) and a small tunneling splitting of Δ = (E1 − E0)/2 ≈ 1.61 cm−1. Similarly, for the vibrational excited states \(\{\left\vert {\nu }_{2}\right\rangle ,\left\vert {\nu }_{3}\right\rangle \}\), we diabatize them and obtain the first excited diabatic vibrational states in the left and right wells as follows
with degenerate diabatic energy of \({{{{{{{{\mathcal{E}}}}}}}}}^{{\prime} }=({E}_{3}+{E}_{2})/2\) and a tunneling splitting of \(\Delta {\prime} =({E}_{3}-{E}_{2})/2\approx 64.05\,{{{{{{{{\rm{cm}}}}}}}}}^{-1}\). A schematic representation of these diabatic states are provided in Fig. 1a. Based on the two diabatic states \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle\) and \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\) in the left well, we define the quantum vibration frequency of the reactant as
which is directly related to the quantum transition of \(\left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}\right\rangle \to \left\vert {\nu }_{{{{{{{{\rm{L}}}}}}}}}^{{\prime} }\right\rangle\).
Further, \({\hat{H}}_{\nu }\) in Eq. (5) is the system-bath Hamiltonian that describes the linear coupling between reaction coordinate \(\hat{R}\) and its phonon bath, expressed as
characterized by the spectral density \({J}_{\nu }(\omega )\equiv (\pi /2){\sum }_{j}({c}_{j}^{2}/{\omega }_{j})\delta (\omega -{\omega }_{j})\). Here, we use the Drude–Lorentz model \({J}_{\nu }(\omega )=2{\lambda }_{\nu }{\gamma }_{\nu }\omega /({\omega }^{2}+{\gamma }_{\nu }^{2})\), with γν = 200 cm−1 for the bath characteristic frequency and λν = 83.7 cm−1 for the reorganization energy. In addition, \({\hat{H}}_{{{{{{{{\rm{c}}}}}}}}}\) describes the loss of cavity photons, through the non-cavity modes \(\{{\tilde{x}}_{j}\}\) that directly coupled to the cavity \({\hat{q}}_{{{{{{{{\rm{c}}}}}}}}}\), expressed as
and the photon-loss bath spectral density is \({J}_{{{{{{{{\rm{c}}}}}}}}}(\omega )\equiv (\pi /2){\sum }_{j}({\tilde{c}}_{j}^{2}/{\tilde{\omega }}_{j})\delta (\omega -{\tilde{\omega }}_{j})=(\omega /{\tau }_{{{{{{{{\rm{c}}}}}}}}})\exp (-\omega /{\omega }_{{{{{{{{\rm{m}}}}}}}}})\), where τc is the cavity lifetime36, and we had assumed that photon loss satisfies strict Ohmic dissipation. In other words, as the cutoff frequency ωm → ∞, the photon bath dynamics reach the Markovian limit36,79. By performing a normal mode transformation, one can obtain a simple system-bath model that is described by an effective spectral density (which is of the Brownian oscillator form36). Details are provided in Supplementary Note 2, Section A.
Rate constant calculations
We use hierarchical equations of motion (HEOM) to simulate the population dynamics and obtain the VSC-modified rate constant, see details in Supplementary Note 1. Here, we treat \({\hat{H}}_{{{{{{{{\rm{M}}}}}}}}}\) as the quantum subsystem and represent it using the vibrational eigenstates \(\{\left\vert {\nu }_{0}\right\rangle ,\left\vert {\nu }_{1}\right\rangle ,\ldots \}\), and the rest terms in the Hamiltonian are treated as the bath in HEOM, see details in Supplementary Note 2. The population dynamics of the “reactant” is computed as \({P}_{{{{{{{{\mathcal{R}}}}}}}}}(t)={{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{{\rm{S}}}}}}}}}[(1-\hat{h}){\hat{\rho }}_{{{{{{{{\rm{S}}}}}}}}}(t)]\), where the trace \({{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{{\rm{S}}}}}}}}}\) is performed along the system DOF (which is the reaction coordinate \(\hat{R}\)), and \(\hat{h}=h(\hat{R}-{R}^{{{{\ddagger}}} })\) is the Heaviside operator with R‡ = 0 as the dividing surface for model potential \(V(\hat{R})\) (in Eq. (37)). The forward rate constant is obtained by evaluating35,36
where \({\chi }_{{{{{{{{\rm{eq}}}}}}}}}\equiv {P}_{{{{{{{{\mathcal{R}}}}}}}}}/{P}_{{{{{{{{\mathcal{P}}}}}}}}}\) denotes the ratio of equilibrium population between the reactant and product, see Supplementary Note 3. For the symmetric double potential model considered in this work, χeq = 1. The limit t → tp represents that the dynamics have already entered the rate process regime (linear response regime) and tp represents the “plateau time” of the time-dependent rate which is equivalent to a flux-side time correlation function formalism27,36. Details of the simulations are provided in Supplementary Note 3, and example flux-side time correlation functions are provided in Supplementary Fig. 1.
For the FGR-based theory, we use the value of the k0 (outside the cavity rate constant) obtained from the HEOM simulation and report k/k0 = 1 + α ⋅ kVSC/k0, where the α = 0.5 is an ad hoc re-scaling factor needed to bring the value of FGR rate constant to the consistent range with the HEOM results.
Data availability
The data that support the findings of this work are available at https://github.com/Okita0512/VSC_HEOM.
Code availability
The source code for HEOM used in this study is available at https://github.com/hou-dao/OpenQuant. The source code for simulating the FGR rate constants, temperature dependence, and resonance condition at the normal incidence is available at https://github.com/Okita0512/VSC_HEOM.
References
Thomas, A. et al. Ground-state chemical reactivity under vibrational coupling to the vacuum electromagnetic field. Angew. Chem. Int. Ed. 55, 11462–11466 (2016).
Thomas, A. et al. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 363, 615–619 (2019).
Vergauwe, R. M. A. et al. Modification of enzyme activity by vibrational strong coupling of water. Angew. Chem. Int. Ed. 58, 15324–15328 (2019).
Thomas, A. et al. Ground state chemistry under vibrational strong coupling: dependence of thermodynamic parameters on the rabi splitting energy. Nanophotonics 9, 249–255 (2020).
Hirai, K., Takeda, R., Hutchison, J. A. & Uji-i, H. Modulation of prins cyclization by vibrational strong coupling. Angew. Chem. Int. Ed. 59, 5332–5335 (2020).
Hirai, K., Hutchison, J. A. & Uji-i, H. Recent progress in vibropolaritonic chemistry. ChemPlusChem 85, 1981–1988 (2020).
Sau, A. et al. Modifying Woodward-Hoffmann stereoselectivity under vibrational strong coupling. Angew. Chem. Int. Ed. 60, 5712–5717 (2021).
Nagarajan, K., Thomas, A. & Ebbesen, T. W. Chemistry under vibrational strong coupling. J. Am. Chem. Soc. 143, 16877–16889 (2021).
Bai, J. et al. Vibrational coupling with o-h stretching increases catalytic efficiency of sucrase in Fabry-Pérot microcavity. Biochem. Biophys. Res. Commun. 652, 31–34 (2023).
Ahn, W., Triana, J. F., Recabal, F., Herrera, F. & Simpkins, B. S. Modification of ground-state chemical reactivity via light-matter coherence in infrared cavities. Science 380, 1165–1168 (2023).
Lather, J., Bhatt, P., Thomas, A., Ebbesen, T. W. & George, J. Cavity catalysis by cooperative vibrational strong coupling of reactant and solvent molecules. Angew. Chem. Int. Ed. 58, 10635–10638 (2019).
Lather, J. & George, J. Improving enzyme catalytic efficiency by co-operative vibrational strong coupling of water. J. Phys. Chem. Lett. 12, 379–384 (2020).
Hiura, H. & Shalabney, A. Vacuum-field catalysis: accelerated reactions by vibrational ultra strong coupling. ChemRxiv https://chemrxiv.org/engage/chemrxiv/article-details/60c75a419abda27db8f8ebdc (2021).
Lather, J., Thabassum, A. N. K., Singh, J. & George, J. Cavity catalysis: modifying linear free-energy relationship under cooperative vibrational strong coupling. Chem. Sci. 13, 195–202 (2022).
Li, X., Mandal, A. & Huo, P. Theory of mode-selective chemistry through polaritonic vibrational strong coupling. J. Phys. Chem. Lett. 12, 6974–6982 (2021).
Mandal, A. et al. Theoretical advances in polariton chemistry and molecular cavity quantum electrodynamics. Chem. Rev. 123, 9786–9879 (2023).
Simpkins, B. S., Dunkelberger, A. D. & Vurgaftman, I. Control, modulation, and analytical descriptions of vibrational strong coupling. Chem. Rev. 123, 5020–5048 (2023).
Imperatore, M. V., Asbury, J. B. & Giebink, N. C. Reproducibility of cavity-enhanced chemical reaction rates in the vibrational strong coupling regime. J. Chem. Phys. 154, 191103 (2021).
Wiesehan, G. D. & Xiong, W. Negligible rate enhancement from reported cooperative vibrational strong coupling catalysis. J. Chem. Phys. 155, 241103 (2021).
Verdelli, F. et al. Polaritonic chemistry enabled by non-local metasurfaces. https://doi.org/10.48550/arXiv.2402.15296 (2024).
Simpkins, B. S., Dunkelberger, A. D. & Owrutsky, J. C. Mode-specific chemistry through vibrational strong coupling (or a wish come true). J. Phys. Chem. C 125, 19081–19087 (2021).
Fidler, A. P., Chen, L., McKillop, A. M. & Weichman, M. L. Ultrafast dynamics of CN radical reactions with chloroform solvent under vibrational strong coupling. J. Chem. Phys. 159, 164302 (2023).
Chen, L., Fidler, A. P., McKillop, A. M. & Weichman, M. L. Exploring the impact of vibrational cavity coupling strength on ultrafast cn + c-c6h12 reaction dynamics. Nanophotonics 13, 2591–2599 (2024).
Li, T. E., Nitzan, A. & Subotnik, J. E. On the origin of ground-state vacuum-field catalysis: equilibrium consideration. J. Chem. Phys. 152, 234107 (2020).
Campos-Gonzalez-Angulo, J. A. & Yuen-Zhou, J. Polaritonic normal modes in transition state theory. J. Chem. Phys. 152, 161101 (2020).
Schäfer, C., Flick, J., Ronca, E., Narang, P. & Rubio, A. Shining light on the microscopic resonant mechanism responsible for cavity-mediated chemical reactivity. Nat. Commun. 13, 7817 (2021).
Li, X., Mandal, A. & Huo, P. Cavity frequency-dependent theory for vibrational polariton chemistry. Nat. Commun. 12, 1315 (2021).
Lindoy, L. P., Mandal, A. & Reichman, D. R. Resonant cavity modification of ground-state chemical kinetics. J. Phys. Chem. Lett. 13, 6580–6586 (2022).
Wang, D. S., Neuman, T., Yelin, S. F. & Flick, J. Cavity-modified unimolecular dissociation reactions via intramolecular vibrational energy redistribution. J. Phys. Chem. Lett. 13, 3317–3324 (2022).
Du, M., Poh, Y. R. & Yuen-Zhou, J. Vibropolaritonic reaction rates in the collective strong coupling regime: Pollak-grabert-hänggi theory. J. Phys. Chem. C 127, 5230–5237 (2023).
Campos-Gonzalez-Angulo, J. A., Poh, Y. R., Du, M. & Yuen-Zhou, J. Swinging between shine and shadow: theoretical advances on thermally activated vibropolaritonic chemistry. J. Chem. Phys. 158, 230901 (2023).
Mandal, A., Li, X. & Huo, P. Theory of vibrational polariton chemistry in the collective coupling regime. J. Chem. Phys. 156, 014101 (2022).
Yang, P.-Y. & Cao, J. Quantum effects in chemical reactions under polaritonic vibrational strong coupling. J. Phys. Chem. Lett. 12, 9531–9538 (2021).
Sun, J. & Vendrell, O. Suppression and enhancement of thermal chemical rates in a cavity. J. Phys. Chem. Lett. 13, 4441–4446 (2022).
Lindoy, L. P., Mandal, A. & Reichman, D. R. Quantum dynamical effects of vibrational strong coupling in chemical reactivity. Nat. Commun. 14, 2733 (2023).
Ying, W. & Huo, P. Resonance theory and quantum dynamics simulations of vibrational polariton chemistry. J. Chem. Phys. 159, 084104 (2023).
Hu, D., Ying, W. & Huo, P. Resonance enhancement of vibrational polariton chemistry obtained from the mixed quantum-classical dynamics simulations. J. Phys. Chem. Lett. 14, 11208–11216 (2023).
Nitzan, A. Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems. Oxford Graduate Texts (Oxford, New York, 2006).
Hänggi, P., Talkner, P. & Borkovec, M. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62, 251–341 (1990).
Taylor, M. A. D., Mandal, A., Zhou, W. & Huo, P. Resolution of gauge ambiguities in molecular cavity quantum electrodynamics. Phys. Rev. Lett. 125, 123602 (2020).
Mukamel, S. Principles of Nonlinear Optical Spectroscopy (Oxford University Press, 1995).
Castellanos, M. A. & Huo, P. Enhancing singlet fission dynamics by suppressing destructive interference between charge-transfer pathways. J. Phys. Chem. Lett. 8, 2480–2488 (2017).
Saller, M. A. C., Lai, Y. & Geva, E. Cavity-modified fermi’s golden rule rate constants from cavity-free inputs. J. Phys. Chem. C. 127, 3154–3164 (2023).
Saller, M. A. C., Lai, Y. & Geva, E. Cavity-modified Fermi’s golden rule rate constants: beyond the single mode approximation. J. Chem. Phys. 159, 151105 (2023).
Ying, W., Taylor, M. A. D. & Huo, P. Resonance theory of vibrational polariton chemistry at the normal incidence. Nanophotonics 13, 2601–2615 (2024).
Wu, M. W. & Ning, C. Z. A novel mechanism for spin dephasing due to spin-conserving scatterings. Eur. Phys. J. B 18, 373–376 (2000).
Gridnev, V. N. Theory of Faraday rotation beats in quantum wells with large spin splitting. JETP Lett. 74, 380–383 (2001).
Brand, M. A. et al. Precession and motional slowing of spin evolution in a high mobility two-dimensional electron gas. Phys. Rev. Lett. 89, 236601 (2002).
Grimaldi, C. Electron spin dynamics in impure quantum wells for arbitrary spin-orbit coupling. Phys. Rev. B 72, 075307 (2005).
Lü, C., Cheng, J. L. & Wu, M. W. Hole spin dephasing in p-type semiconductor quantum wells. Phys. Rev. B 73, 125314 (2006).
Leyland, W. J. H. et al. Oscillatory Dyakonov-Perel spin dynamics in two-dimensional electron gases. Phys. Rev. B 76, 195305 (2007).
Marcus, R. & Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985).
Gladkikh, V., Burshtein, A. I. & Rips, I. Variation of the resonant transfer rate when passing from nonadiabatic to adiabatic electron transfer. J. Phys. Chem. A 109, 4983–4988 (2005).
Huo, P., Miller, T. F. & Coker, D. F. Communication: predictive partial linearized path integral simulation of condensed phase electron transfer dynamics. J. Chem. Phys. 139, 151103 (2013).
Lawrence, J. E., Fletcher, T., Lindoy, L. P. & Manolopoulos, D. E. On the calculation of quantum mechanical electron transfer rates. J. Chem. Phys. 151, 114119 (2019).
Singh, J., Lather, J. & George, J. Solvent dependence on cooperative vibrational strong coupling and cavity catalysis. ChemPhysChem 24, e202300016 (2023).
Li, T. E., Cui, B., Subotnik, J. E. & Nitzan, A. Molecular polaritonics: chemical dynamics under strong light–matter coupling. Annu. Rev. Phys. Chem. 73, 43–71 (2021).
Vurgaftman, I., Simpkins, B. S., Dunkelberger, A. D. & Owrutsky, J. C. Comparative analysis of polaritons in bulk, dielectric slabs, and planar cavities with implications for cavity-modified reactivity. J. Chem. Phys. 156, 034110 (2022).
Ribeiro, R. F. Multimode polariton effects on molecular energy transport and spectral fluctuations. Commun. Chem. 5, 48 (2022).
Jaynes, E. & Cummings, F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 51, 89–109 (1963).
Hove, L. V. The occurrence of singularities in the elastic frequency distribution of a crystal. Phys. Rev. 89, 1189–1193 (1953).
Yoo, D. et al. Ultrastrong plasmon–phonon coupling via epsilon-near-zero nanocavities. Nat. Photonics 15, 125–130 (2021).
Dayal, G., Morichika, I. & Ashihara, S. Vibrational strong coupling in subwavelength nanogap patch antenna at the single resonator level. J. Phys. Chem. Lett. 12, 3171–3175 (2021).
del Pino, J., Feist, J. & Garcia-Vidal, F. J. Quantum theory of collective strong coupling of molecular vibrations with a microcavity mode. N. J. Phys. 17, 053040 (2015).
Shalabney, A. et al. Coherent coupling of molecular resonators with a microcavity mode. Nat. Commun. 6, 5981 (2015).
Sidler, D. et al. Unraveling a cavity induced molecular polarization mechanism from collective vibrational strong coupling. J. Phys. Chem. Lett. 15, 5208–5214 (2024).
Cao, J. Generalized resonance energy transfer theory: applications to vibrational energy flow in optical cavities. J. Phys. Chem. Lett. 13, 10943–10951 (2022).
Chen, H.-T., Zhou, Z., Sukharev, M., Subotnik, J. E. & Nitzan, A. Interplay between disorder and collective coherent response: superradiance and spectral motional narrowing in the time domain. Phys. Rev. A. 106, 053703 (2022).
Pandya, R. et al. Tuning the coherent propagation of organic exciton-polaritons through dark state delocalization. Adv. Sci. 9, 2105569 (2022).
Kim, K. et al. Sensitive control of broad-area semiconductor lasers by cavity shape. APL Photonics 7, 056106 (2022).
Georgiou, K., Jayaprakash, R. & Lidzey, D. G. Strong coupling of organic dyes located at the surface of a dielectric slab microcavity. J. Phys. Chem. Lett. 11, 9893–9900 (2020).
Canales, A., Baranov, D. G., Antosiewicz, T. J. & Shegai, T. Abundance of cavity-free polaritonic states in resonant materials and nanostructures. J. Chem. Phys. 154, 024701 (2021).
Thomas, P. A., Tan, W. J., Kravets, V. G., Grigorenko, A. N. & Barnes, W. L. Non-polaritonic effects in cavity-modified photochemistry. Adv. Mater. 36, 2309393 (2024).
Thomas, P. A. & Barnes, W. L. Selection bias in strong coupling experiments. J. Phys. Chem. Lett. 15, 1708–1710 (2024).
Schäfer, C., Fojt, J., Lindgren, E. & Erhart, P. Machine learning for polaritonic chemistry: accessing chemical kinetics. J. Am. Chem. Soc. 146, 5402–5413 (2024).
Topaler, M. & Makri, N. Quantum rates for a double well coupled to a dissipative bath: accurate path integral results and comparison with approximate theories. J. Chem. Phys. 101, 7500–7519 (1994).
Shi, Q., Zhu, L. & Chen, L. Quantum rate dynamics for proton transfer reaction in a model system: effect of the rate promoting vibrational mode. J. Chem. Phys. 135, 044505 (2011).
Colbert, D. T. & Miller, W. H. A novel discrete variable representation for quantum mechanical reactive scattering via the s-matrix Kohn method. J. Chem. Phys. 96, 1982–1991 (1992).
Garg, A., Onuchic, J. N. & Ambegaokar, V. Effect of friction on electron transfer in biomolecules. J. Chem. Phys. 83, 4491–4503 (1985).
Acknowledgements
This work was supported by the National Science Foundation Award under Grant No. CHE-2244683, as well as by the Air Force Office of Scientific Research under AFOSR Award No. FA9550-23-1-0438. W.Y. appreciates the support of the Esther M. Conwell Graduate Fellowship from the University of Rochester. P.H. appreciates the support of the Cottrell Scholar Award (a program by the Research Corporation for Science Advancement). Computing resources were provided by the Center for Integrated Research Computing (CIRC) at the University of Rochester.
Author information
Authors and Affiliations
Contributions
W.Y. and P.H. designed the research. W.Y. performed the exact quantum dynamics simulations. W.Y. and P.H. derived the analytic rate constant expressions. W.Y. and P.H. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Aldo Isidori. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ying, W., Huo, P. Resonance theory of vibrational strong coupling enhanced polariton chemistry and the role of photonic mode lifetime. Commun Mater 5, 110 (2024). https://doi.org/10.1038/s43246-024-00551-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-024-00551-y
- Springer Nature Limited