Introduction

Topological insulators refer to materials with an insulating bulk but support conductive topological edge states (TESs)1,2. Topological insulators provide a robust framework known as the bulk-edge correspondence. These TESs demonstrate remarkable stability against local perturbations, safeguarded by symmetries including time-reversal and spatial invariance3,4,5. The potential applications of these materials span numerous advanced fields, notably in spintronics and the rapidly evolving domain of quantum computing6,7,8. Over time, these topological concepts have found relevance in various classical systems, such as electronic systems9,10, photonics11,12, phononics13,14,15, and mechanical systems16,17, showcasing their versatile applicability.

Recently, LC circuits have emerged as a highly promising method to realize significant phenomena18,19,20,21,22,23,24,25,26,27,28,29,30,31. For example, LC circuits has been used to study bulk-edge correspondence in high dimensional system22,23, transmission in low dimensional systems24,25,26, and corner states in higher-order topological insulators27,28,29,30,31. Additionally, there is the potential to introduce nonlinear components or operational amplifiers, facilitating the study of topological states in novel physical systems32,33,34,35,36,37,38,39,40. Compared with other classical platforms, LC circuits offer several notable advantages. These circuits can be meticulously engineered following the tight-binding (TB) model, allowing for precise control over their electronic states. This precision is invaluable for experimental validations and applications in various technological domains. They are easy to manufacture, and the TESs are not adversely affected by lattice defects or environmental interactions.

Despite these advantages, challenges arise in dissecting the intricate interplay between topological states and nonlinear media within these circuits. Since TB topological models typically reflect partial bands of artificial microstructures such as photonic crystals, other states are required to participate in nonlinear processes41,42,43,44. The topological states in TB models are often set as the fundamental wave (FW), and the filling ratio of the crystal can be determined through multiple calculations to find another topological state that satisfies the frequency matching condition in the high-frequency band of the structure41,45,46,47. Unlike photonics or other systems, the number of energy bands and topological states in LC circuits is strictly controlled by the number of nodes. The absence of multiple topological states has made previous research with nontrivial topological LC circuits mainly focused on the FW with localized states (LSs) and nonlinear control35,36,37,38,39,40. Although numerous studies have shown that the resonance of topological states can enhance the ability of a system to generate harmonics, the limitations of circuit systems pose challenges in experimentally validating the role of topological state resonance in harmonic enhancement. To overcome these challenges, we introduce the mirror-stacking circuit methodology, which can stack multiple isolated systems to create a composite system, preserving the spatial symmetry of the protected band topology in the subsystems to maintain doubly resonant LSs48.

In our approach, we employ a mirror-stacking approach to superimpose two one-dimensional nonlinear transmission lines, achieving a system with two doubly resonant LSs. The LSs in the system are independent of each other, and the LSs can be transferred to any frequency by changing the hopping. Upon introducing nonlinear components to the circuit, both LSs effectively generate the higher-harmonic waves (HWs). The HWs generated by two LSs exhibit different characteristics. This work primarily investigates the enhancement of both FWs and higher-HWs facilitated by doubly resonant LSs. It is important to note that although FW and HW are localized at the boundary, they are the result of driving the entire circuit, not just the edges. We demonstrate this enhancement mechanism by nonlinear topolectrical circuits, realized through the mirror-stacking method on printed circuit boards (PCB).

Result

Mirror-stacking circuit model

We start with a simple one-dimensional topological transmission circuit, composed of two capacitors Ca and Cb of different sizes. The system is illustrated in the upper diagram of Fig. 1a. We set the points where each capacitor intersects as lattice nodes, using n as the index for each unit cell, and each node is grounded through an inductor. Considering Kirchhoff’s laws, the voltage as the function of angular frequency in circuit can be obtained:

$$\begin{array}{c}\left(\frac{1}{({C}_{a}+{C}_{b}){\omega }^{2}L}-1\right)E\left[\begin{array}{c}{v}_{n}^{a}\\ {v}_{n}^{b}\end{array}\right]=H^{\prime} \left[\begin{array}{c}{v}_{n}^{a}\\ {v}_{n}^{b}\end{array}\right]\\ H^{\prime} =\frac{1}{{C}_{a}+{C}_{b}}\left[\begin{array}{cc}0 & -{C}_{a}-{C}_{b}{e}^{-ik}\\ -{C}_{a}-{C}_{b}{e}^{ik} & 0\end{array}\right]\end{array}$$
(1)

where \({v}_{n}^{a}\) represents the voltage at node a of the n-th lattice cell. Setting Ca = 20 pF, Cb = 56 pF, L = 4.7 μH, the eigenvalues of H’ are shown in Fig. 1b.

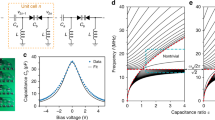
Fig. 1: Design and implementation of mirror stack circuit.
figure 1

a Schematic representation of a one-dimensional single chain circuit and its mirror-stacked counterpart. b Band structure depiction for the single chain circuit. c Band structures of two distinct mirror-stacked circuit configurations. Both configurations maintain identical Ca and Cb values but differ in inter-chain capacitance: C1 = 0.4Cb (solid lines) and C1 = 2Cb (dashed lines). Red and blue represent the contributions of different subsystems. d Eigenvalue spectra of finite-sized systems, varying C1 while maintaining constant Ca and Cb. The areas marked in red are topological bound states in the continuum. e, f Correlation between eigenfrequencies and the capacitance ratio α = Ca/Cb in finite circuits. e illustrates the low-frequency band, while (f) represents the high-frequency band. The lattice has 15 sites. A topologically trivial gap is observed when α > 1, whereas α < 1 yields a non-trivial gap. Red dotted curves indicate the upper and lower bounds of the bandgap. g Variation of capacitance Ca with applied bias voltage. Displayed dots represent mean values from 20 distinct measurements using an LCR meter, while the black curve represents the fitting function.

Full size image

Limited by the number of bandgaps and LS frequencies of a single-chain system, if nonlinear components are introduced into the system to generate HWs, only one of the FW and HWs can occupy the LS. To construct a one-dimensional circuit with dual LSs, nodes in two identical chains are connected through a capacitor C1, as illustrated in Fig. 1a. The resulting Kirchhoff equation matrix for the dual-chain system is (see Supplementary Note 1 for detail):

$$\left(\frac{1}{{C}_{sum}{\omega }^{2}L}-1\right)E\left[\begin{array}{c}{v}_{n}^{a}\\ {v}_{n}^{b}\\ {v}_{n}^{c}\\ {v}_{n}^{d}\end{array}\right]=H\left[\begin{array}{c}{v}_{n}^{a}\\ {v}_{n}^{b}\\ {v}_{n}^{c}\\ {v}_{n}^{d}\end{array}\right]$$
(2)

Csum represents the total capacitance at the node, Csum = Ca + Cb + C1. E is the identity matrix. The H matrix of the dual-chain system is:

$$H=\frac{1}{{C}_{sum}}\left[\begin{array}{cccc}0 & -{C}_{a}-{C}_{b}{e}^{-ik} & -{C}_{1} & 0\\ -{C}_{a}-{C}_{b}{e}^{ik} & 0 & 0 & -{C}_{1}\\ -{C}_{1} & 0 & 0 & -{C}_{c}-{C}_{d}{e}^{-ik}\\ 0 & -{C}_{1} & -{C}_{c}-{C}_{d}{e}^{ik} & 0\end{array}\right]$$
(3)

We present the eigenvalues of H for two different scenarios: C1 = 0.4Cb (solid lines) and C1 = 2Cb (dashed lines), to investigate the impact of C1 on the system eigenvalues, as shown in Fig. 1c. The red and blue lines represent contributions from two different subchains. The eigenvalues obtained from H are shifted compared to the isolated chain, and the eigenvalues contributed by the two subchains are further separated as C1 increases. We explain this phenomenon through a similarity transformation matrix S = τ0 ⊗ E - iτ2 ⊗ E. The H matrix can be transformed by S into two hypothetical chains with independent subspaces to get \(\tilde{H}={S}^{-1}HS\), where τ0 and τ2 are Pauli matrices:

$$\tilde{H}=\frac{1}{{C}_{sum}}\left[\begin{array}{cccc}-{C}_{1} & -{C}_{a}-{C}_{b}{e}^{-ik} & 0 & 0\\ -{C}_{a}-{C}_{b}{e}^{ik} & -{C}_{1} & 0 & 0\\ 0 & 0 & {C}_{1} & -{C}_{a}-{C}_{b}{e}^{-ik}\\ 0 & 0 & -{C}_{a}-{C}_{b}{e}^{ik} & {C}_{1}\end{array}\right]$$
(4)

These two hypothetical chains lack a coupling capacitor between them. In contrast to the isolated circuit H’, the diagonal elements here are influenced by C1, resulting in a general increase and decrease in the eigenvalues. The energy levels of both subchains exhibit symmetry about the zero-energy level (eigenvalue = 0). Each hypothetical subchain maintains chiral symmetry, with its topological properties determinable through hopping transitions and characterized by the winding number49:

$$w={\int }_{0}^{2\pi }\frac{dk}{2\pi i}\frac{d}{dk}\log \det \left[{h}_{sub}(k)\right]$$
(5)

where hsub represents the elements in the subchain Hamiltonian. Furthermore, since there is no coupling between them, their topological properties do not interfere with each other. Through appropriate interchain coupling, any states of the two subchains can coexist at the same energy level with opposite parity, such as bulk states and LSs. This also implies that the LS from one subchain can pass across the bulk state of another subsystem without hybridization, leading to the formation of bound states in the continuum. In a mirror-stacked circuit system of length N, eigenvalue outcomes under various C1 conditions are derived from the 4 N × 4 N Kirchhoff matrix (see Supplementary Note 2 for detail), as shown in Fig. 1d. With the C1/Cb ratio increasing from 0 to 2, the topological states in the subsystem transition from LSs to topological bound states in the continuum, eventually returning to LSs, as depicted in Fig. 1d (white-red-white underpainting). This study primarily focuses on identifying LSs that satisfy a frequency tripling relationship, in order to facilitate resonance that enhances HWs.

Note that the eigenvalues derived from H are not indicative of the circuit’s eigenfrequencies. Due to the mapping established by the aforementioned equation, the eigenfrequencies correlate with the eigenvalues in the following manner:

$$f=\frac{1}{2\pi \sqrt{{C}_{sum}L}\sqrt{1+\epsilon }}$$
(6)

where f represents the frequency corresponding to the eigenvalues ε. We can obtain two finite bandgaps for the circuit based on the matrix \(\tilde{H}\):

$$\left\{\begin{array}{c}\frac{1}{\sqrt{L\left[{C}_{sum}+{C}_{1}+|{C}_{a}-{C}_{b}|\right]}} < \,{\omega }_{ga{p}_{1}} < \frac{1}{\sqrt{L\left[{C}_{sum}+{C}_{1}-|{C}_{a}-{C}_{b}|\right]}}\\ \frac{1}{\sqrt{L\left[{C}_{sum}-{C}_{1}+|{C}_{a}-{C}_{b}|\right]}} < \,{\omega }_{ga{p}_{2}} < \frac{1}{\sqrt{L\left[{C}_{sum}-{C}_{1}-|{C}_{a}-{C}_{b}|\right]}}\end{array}\right.$$
(7)

The frequencies of the two LSs as follows:

$$\begin{array}{c}{f}_{LS1}=\frac{1}{2\pi \sqrt{({C}_{sum}+{C}_{1})L}}\\ {f}_{LS2}=\frac{1}{2\pi \sqrt{({C}_{sum}-{C}_{1})L}}\end{array}$$
(8)

Hence, a substantial C1 value is crucial to facilitate resonance between the two LSs. Define the capacitance ratio as α = Ca/Cb, and set C1 = 370 pF for analyzing its impact on the circuit, as illustrated in Fig. 1e, f. For α values less than 1, both bandgaps of the circuit encompass a LS with nontrivial topology. As Ca decreases, the circuit increasingly aligns with a topologically nontrivial state. Conversely, increasing Ca to make α exceed 1 leads to trivial bandgaps devoid of LSs.

Subsequently, we introduce a nonlinear capacitor configuration where each Ca comprises a pair of back-to-back varactors. The nonlinear capacitance Ca was quantified using an LCR meter, and its capacitance decreases as the absolute value of the bias voltage increases, as shown in Fig. 1g. For theoretical analysis, we established a function to describe capacitance variation as a function of bias voltage, represented as:

$$\beta \approx A+B|{V}_{bias}{|}^{2}$$
(9)

β ≡ Cb/ Ca, A = 1.75, B = 0.5. The fitting function is displayed in Fig. 1g. In a special scenario where αnl ≡ 1/β reaches its maximum of 1/A (<1), the circuit exhibits LSs at all voltage levels. With nonlinear characteristics causing αnl to effectively decrease with increasing voltage, the circuit is driven further into a topologically nontrivial state.

Circuit simulation design and resonance analysis

A simulation was conducted to analyze the response of the mirror circuit within a linear system. Owing to the mirror system’s symmetry, the wavefunctions of the two chains, as derived from Eq. 2, exhibit identical absolute values but opposite signs at fLS1, and congruent signs at fLS2 (see Supplementary Note 3 for detail). When driven by a sine wave source, the circuit demonstrates the following responses: a phase difference of π at fLS1, and 2π (equivalently 0) at fLS2 between the voltages in the two chains. This behavior was validated by introducing sinusoidal signals of varying phases through ports S1 and S2. Figure 2a displays the voltage response of \({v}_{1}^{a}\) in the circuit at different frequencies when Ca = 20 pF (lossless case). Both sources have the same phase, the LS at fLS2 is excited. When the phase difference between the two sources is π, the LS at fLS1 is excited. For the ensuing nonlinear harmonic generation process, the concurrent presence of two LSs is essential. Consequently, the signal was input through S1 with S2 grounded. The resulting curves, depicted in Fig. 2b, include two resonant peaks at different frequencies and a valley (fLS1, fLS2, fLS3), with fLS3 being the mirror-symmetric point.

$${f}_{LS3}=\frac{{\omega }_{3}}{2\pi }=\frac{1}{\sqrt{{C}_{sum}L}}$$
(10)
Fig. 2: Simulation of the circuit response and phase.
figure 2

a Circuit response when two signal sources are in phase compared to a phase difference of π. In-phase alignment yields a response solely at fLS2, while a π phase difference induces a response at fLS1. b Response of the circuit to a single source, exhibiting two localized states (LSs), fLS1 and fLS2. fLS3 is the mirror-symmetric point. c Phase variation of the boundary node with frequency, as derived from (b). d, e Response curves for a topologically trivial circuit. f, g Response curve of a topologically non-trivial circuit. The a/c nodes (va/vc) are odd nodes, while b/d nodes (vb/vd) are even nodes. h Response voltages at each node in both trivial and non-trivial circuits under LSs.

Full size image

The phase of \({v}_{1}^{a}\) and \({v}_{1}^{c}\) as a function of frequency is shown in Fig. 2c. At fLS3, a phase transition occurs, the frequency is lower than fLS3, the phase difference remains constant at π, and when the frequency is greater than fLS3, the phase difference becomes 2π. The change in the phase difference is attributed to the mass term on the diagonal of Eq. 4. Note that the single source can only excite one of the chains, while the other chain serves as the resonance for the excited chain, and thus their phases satisfy the eigenmodes.

Each node is numbered in the order from left to right and from a to d in the lattice. Therefore, all nodes labeled a and c are odd, while nodes b and d are even. The responses of all nodes across varying frequencies were quantified, and the results are shown in Fig. 2d, e. Notably, an enhanced response was observed in odd-numbered nodes at fLS1 and fLS2. Upon interchanging Ca and Cb (α > 1) the response of the trivial circuit was assessed, with results presented in Fig. 2f, g. Through comparison, it was found that after swapping the capacitors, even nodes remain unaffected, while the voltage enhancement at odd nodes at fLS1 and fLS2 disappears and is suppressed. This variation is ascribed to the circuit’s topological phase shift, rendering it devoid of transmission modes. We measured the voltage at each node for both trivial and non-trivial circuits at frequencies fLS1 and fLS2, as shown in Fig. 2h. It can be observed that the transmission modes of the two circuits differ, and there is a noticeable difference in the voltage intensity localized at the edges. This confirms the enhancing effect of LS on the circuit.

Incorporating Ca as a nonlinear capacitor, Eq. 3 is reformulated for any m-th order harmonic circuit as follows (see Supplementary Note 4 for detail):

$${{H}_{nl}}=\left[ \begin{array}{cccc} -{{C}_{a}}\cos {{k}_{m}}-{{C}_{sum}}+{{C}_{b}} & -i{{C}_{a}}\sin {{k}_{m}} & {{C}_{1}} & 0 \\ i{{C}_{a}}\sin {{k}_{m}} & {{C}_{a}}\cos {{k}_{m}}-{{C}_{sum}}-{{C}_{b}} & 0 & {{C}_{1}} \\ {{C}_{1}} & 0 & -{{C}_{a}}\cos {{k}_{m}}-{{C}_{sum}}+{{C}_{b}} & -i{{C}_{a}}\sin {{k}_{m}} \\ 0 & {{C}_{1}} & i{{C}_{a}}\sin {{k}_{m}} & {{C}_{a}}\cos {{k}_{m}}-{{C}_{sum}}-{{C}_{b}}\end{array} \right]$$
(11)

Hnl can still be separated into two subsystems with independent subspaces using the transfer matrix S.

Experimental observation of nonlinear circuits

Figure 3a displays the experimental PCB. The response of the nonlinear mirror-stacked system was measured using a broadband signal, depicted in Fig. 3b. The response curve features two LSs at distinct frequencies, aligning with theoretical predictions. The voltage was set at 4 V, and source frequencies (fs) of 2.68 MHz and 8.04 MHz were chosen to excite LSs, as illustrated in Fig. 3c. Distinct behaviors of both signals are observed, with localization at the system’s edges. The rapid decay beyond the boundary is likely due to the coupling with the topological LSs. Additionally, the circuit’s response under dual-source conditions was examined. The LSs in Fig. 3c demonstrate pronounced responses exclusively at the boundaries. Consequently, the response voltages \({v}_{1}^{a}\) for the two LSs under varying phase differences were observed, as presented in Fig. 3d, e. The measurement results align with the linear simulation outcomes. When the phases of the two sources are in sync, the response at fLS2 is maximized, while the response at fLS1 is minimized. Conversely, when there is a phase difference of π, the situation is reversed.

Fig. 3: Nonlinear circuit response and excitation of different sources.
figure 3

a Depicts the experimental printed circuit board. The image on the left provides a magnified view of the highlighted rectangular area on the right. S1 and S2 are the input ports, C1, Ca, and Cb are capacitors, and L is an inductor. b The response of the experimental circuit to a single source across various frequencies. The observed dual peaks correspond to the frequencies of the two localized states (LSs) in the circuit, fLS1 and fLS2. c Shows the excitation of circuit when the source frequency is set to the two LSs frequencies, as identified in (b), with subsequent observation of voltage responses at various nodes. d, e Display the intensity variation of node 1 as a function of phase difference at frequencies fLS1 and fLS2, respectively, when utilizing two sources.

Full size image

Within the nonlinear circuit, bias voltage variations between nodes influence the resonant frequencies. Observations made using a broadband signal with different voltages (2 V to 8 V) are shown in Fig. 4a. With Ca being voltage-dependent, Eq. 8 is reformulated as follows:

$$\begin{array}{c}{f}_{LS1}=\frac{1}{2\pi \sqrt{\left[{C}_{b}+2{C}_{1}+{C}_{a}(V)\right]L}}\\ {f}_{LS2}=\frac{1}{2\pi \sqrt{\left[{C}_{b}+{C}_{a}(V)\right]L}}\end{array}$$
(12)
Fig. 4: Harmonic generation in two topological bandgaps.
figure 4

a Demonstrates the frequency response of the printed circuit board (PCB) to varying input voltages, with the curves transitioning from red to black representing voltages from 2 V to 8 V. b Displays the third harmonic distortion as a function of input voltage at the frequency of fLS1. The red and blue lines represent different subchains. c, d The inverse participation ratio of the circuit at different frequencies is obtained by FFT analysis of multiple nodes. e, f The fundamental wave (FW) and third harmonic generation (THG) responses of the PCB when excited at 2.68 MHz (fLS1) and 8.04 MHz (fLS2).

Full size image

Subsequently, influence of Ca on the PCB resonant frequency fLS1 is notably less compared to its effect on fLS2. It can be observed that fLS1 hardly changes with voltage and remains constant at 2.68 MHz. On the other hand, fLS2 gradually increases with voltage, ranging from 7.941 MHz to 8.061 MHz, and stabilizes when the voltage reaches 5 V. This behavior is governed by the C–V curve of the nonlinear capacitor in Fig. 1c. The generation of HWs is driven by the nonlinear capacitor, and HWs are influenced by the input voltage. The efficiency of harmonic generation is assessed using the third harmonic distortion (THD), η = PTHG/PFW. PFW and PTHG represent the power of the FW and third harmonic components, respectively. Since fs = fLS1, the FW and HW are driven by the LS, so we observe the power of the FW and HW components of \({v}_{1}^{a}\) as PFW and PTHG. We derived the THD as a function of voltage under the resonance of the dual LSs based on different voltages for fLS1 in Fig. 4b. At lower voltages, fLS2 ≠ 3fLS1 and the nonlinear effect of the Ca capacitance is not so significant. As the voltage increases, the difference between fLS2 and 3fLS1 decreases, leading to a gradual increase in THD. When the voltage reaches 5 V, the THD stabilizes.

Single-frequency signals of varying frequencies were input at 6 V (with a frequency increment of 0.01 MHz) to observe the HWs. HWs at fLS2, driven by the bulk state, were compared to those at fLS1, which are driven by dual dual LS resonance. Figure 4c, d present the inverse participation ratio (IPR) \({\sum }_{k}{|{v}_{k}^{f}|}^{4}/{({\sum }_{k}{|{v}_{k}^{f}|}^{2})}^{2}\) as a quantitative measure of HW signal localization. Where k represents the node index. f represents different frequencies in the FFT results. The green dashed line represents three times the input frequency. A larger IPR corresponds to a more localized profile50. Note that, in the mirrored stacking system, the presence of two localized nodes affects the IPR. Considering the attenuation caused by impedance, calculations were performed using the first 8 nodes voltages of one chain. As depicted in Fig. 4c, with the input frequency nearing 2.68 MHz, an increase in response voltage is observed, bringing fLS2 closer to triple the frequency of fLS1. The HWs become more localized. However, as the input frequency continues to exceed 2.68 MHz, the response voltage gradually decreases, and the difference between fLS2 and 3fLS1 to increase, and the IPR of HWs decreases. Figure 4d illustrates that third harmonic generation (THG) consistently occurs within the bulk state, leading to a persistently lower harmonic IPR.

Signals with input frequencies of 2.68 MHz and 8.04 MHz at 6 V were applied, and the results are shown in Fig. 4e, f. HWs of fLS1 are localized at the circuit’s edge, in contrast to HWs of fLS2 which disperse throughout the circuit, attenuated by its impedance. The maximum values of the FW and THG powers, denoted as PFW and PTHG, were determined for the systems. Consequently, the THD for the two input waves were calculated to be 4.570 × 10−3 and 2.903 × 10−4, respectively. Even though the FW of fLS2 is stronger, the HWs of fLS1, driven by LS, result in stronger amplitudes and THD. The primary focus of this study is on HWs concentrated at the circuit boundary. The subsequent PTHG only observes the THG power at the boundary, rather than searching for strong HWs within the system.

Discussion

Adjusting the coupling capacitance C1 to 310 pF in the nonlinear PCB2 (compared to PCB1 with C1 = 370 pF) further confirmed the link between dual LS resonance and THD and amplitude enhancement. According to Eq. 12, the resonance of dual LSs was disrupted, and the measurement results of the PCB2 response confirmed this. The response of PCB2 was measured at 6 V using a broadband signal, revealing LS frequencies of fLS4 = 2.88 MHz and fLS5 = 8.13 MHz (the variation in fLS5 is due to component tolerances). There is a significant frequency difference between 3fLS4 and fLS5. Due to the absence of transmission mode in the THG of fLS4, which is drive by a single-node, its maximum value is located at the edge of the circuit.

THD measurement can be effectively conducted by monitoring either node 1 or node 3. Single-frequency signals were applied at 6 V with a frequency increment of 0.01 MHz, covering a source frequency range from 2.6 to 3.0 MHz, to obtain the FFT frequency spectra for both PCB configurations. The results are depicted in Fig. 5a–d. The spectrograms of PCB1, corresponding to various input frequencies, are depicted in Fig. 5c, d. HWs generated by the lower-frequency LS are captured by the other LS, yielding the maximum response of both FW and HWs simultaneously at 2.68 MHz, with response voltages of 5.55 V and 0.37 V and the THD is η1 = 4.575 × 10−3. For PCB2, where HWs generated by the LS are not captured by another LS, the singular peak observed in spectrogram of PCB1 located on the threefold frequency (shown in Fig. 5c) to split into two smaller peaks, as shown in Fig. 5a. Specifically, when the source frequency is fLS4, the amplitude of the HWs increases due to the enhancement of the FW frequency. When the source frequency is fLS5/3, the strong HWs generation is attributed to the LS at fLS5. We extracted the amplitudes at the triple frequency of the source in the FFT spectrum and calculated the THD. In PCB2, the maximum THD occurs around fLS5/3. And η4 at fLS4 is 4.556 × 10−5. Due to the FW frequency not being at its maximum value at fLS5/3 and fLS4 not being the point of highest conversion efficiency, this results in a lower maximum THG amplitude in Fig. 5a compared to Fig. 5c. Their maximum harmonic amplitudes are 0.039 V and 0.036 V. This comparison demonstrates that the resonance of the two LSs can enhance the amplitude and THD. It is evident that η4 is much smaller than η1, with η1 = 100η4. This is due to the absence of resonance between the THG of fLS4 and the LS in the high bandgap. Harmonic power analysis in the PCB revealed that power generated by dual resonance is 90 and 105 times greater than that at fLS4 and fLS5/3, respectively (shown in Fig. 5e). This is attributed to the fact that only one of the FW and HW is driven by the LS, while the other is driven by a single node. When the input frequency is fLS1 for PCB1 and fLS4 and fLS5/3 for PCB2, the THG power at various nodes in the circuit is illustrated in Fig. 5f. THG at fLS4, exhibiting the strongest intensity at the boundaries, confirms harmonic production by a single node. THG at fLS5/3 are also strongest at the boundaries, confirming that the FW driven by a single node can induce the LS of THG. As illustrated in Fig. 5f, the harmonic power from dual resonance notably exceeds that from the other two scenarios

Fig. 5: Harmonic generation in printed circuit board (PCB) under coupled and uncoupled conditions.
figure 5

a–d Present the voltage amplitude versus input frequency plots alongside their FFT spectra, with an input frequency increment of 0.01 MHz. Observations in (a) and (b) correspond to PCB2 (C1 = 310 pF), and (c) and (d) to PCB1 (C1 = 370 pF). e Depicts third harmonic generation (THG) power from both PCB configurations, excited at varying frequencies. The red line is PCB1 and the black line is PCB2. f Illustrates the distribution of THG power across each node, corresponding to the peak source frequencies in (a) and (c). The black line is fLS1 (2.68 MHz), the red line is fLS4 (2.88 MHz), and the blue line is fLS5/3 (2.71 MHz).

Full size image

Conclusion

In summary, this study successfully coupled two isolated subchains through the mirror stacking method. This synthesized system integrates the band topology and energy spectrum from each subchain, which culminates in the emergence of two LSs at distinct frequencies. The coupling strength distinctly influences the frequencies of these LSs. Upon integrating nonlinear components into the system, we observed a notable enhancement in nonlinear conversion efficiency, especially when both the FW and HWs are simultaneously localized. This discovery paves the way for the application of topological states to simultaneously enhance both FW and HWs, extending from one-dimensional circuits to various complex systems. These include higher-order topological corner states in linear systems, as well as extended and skin states in non-Hermitian systems. It provides new perspectives for research on nonlinear harmonic models in photonics and acoustics, contributes to the development of more reliable and efficient nonlinear optical and acoustic devices, and opens up new ways for the advancement of future information processing technologies. However, it is worth noting that the model may have limitations when applied to different fields. This is because the variability of the hopping strengths may be restricted by material characteristics, spatial geometries, and other factors. These limitations should be carefully considered in future applications.

Method

The two mirror stack circuit was implemented on the PCB (Shenzhen JLC Technology Group Co.), with each nonlinear capacitor consisting of hyperabrupt junction tuning varactor (SMV1253-004LF). In the PCB, a 370 pF capacitor is equivalently formed by paralleling 220 pF and 150 pF capacitors. A 310 pF capacitor is created by paralleling a 220 pF capacitor with two 47 pF capacitors. The tolerance of all linear capacitors are 1%. The inductance L, with a rated value of 4.7 μH and a direct current resistance of 14 mΩ, has a 20% tolerance. Using an LCR meter (Tonghui TH2840B), we reduced this accuracy to 2%, finalizing the inductor’s value at 4.3 μH. The C–V curves of nonlinear varactors are measured by an LCR meter. A function generator (Keysight 33500B) supplies the continuous-wave sinusoidal input voltage, and the voltages on successive lattice sites are measured by an oscilloscope (Keysight DSOX4024A) in high-impedance mode.