Introduction

Electrons usually move much faster than nuclei and, for this reason, they play a dominant role in the optical response of two- and three-dimensional materials. Thus, manipulating and controlling electronic motion in its natural timescale, well before the lattice has time to respond, may open an unprecedented platform for charge transport and valleytronics based on electron coherence. Nowadays, we have the technology to produce laser pulses as short as several attoseconds (10−18 s), which enables to track and investigate electron dynamics1,2. By using such technology, techniques such as ultrafast absorption spectroscopy have been carried out to observe electron motion in insulators, semiconductors, and semimetals1,2,3,4,5,6,7, and even in few-layers materials8.

Attosecond and few-femtosecond pulses not only enable to track electron dynamics, but also to trigger unusual charge dynamics. In particular, real-time investigations of charge migration in molecular systems, induced by such ultrashort pulses, have been systematically reported in the literature for almost a decade, providing an unprecedented understanding of the process and opening the way for new control schemes of chemical reactions (the so-called attochemistry)9,10,11,12. Charge migration can be induced by creating a coherent superposition of bound molecular states with a broadband, attosecond, or few-fs pulse. During the free propagation of the system, this coherent superposition induces fast oscillations between the involved states, which, in the case of covering different spatial regions and/or exhibiting quite different electronic properties, may translate into electron transfer from one side of the molecule to another. To our knowledge, similar charge migration processes have not yet been observed in condensed-matter systems, probably because the electrons organize in a quasi continuum of delocalized states (the electronic bands), so that any coherent superposition induced by an ultrashort pulse involves a huge number of states with continuously and smoothly varying electronic properties.

In this manuscript, we demonstrate that laser induced charge migration is possible in materials whose optical response is dominated by excitonic interactions. Excitons can be considered as quasi-particles composed of an electron-hole pair bound via Coulomb interaction. This interaction can only manifest in systems where screening effects are not dominant, as, e.g., non-metallic two-dimensional (2D) materials, where mobility of the remaining electrons is hampered due to the reduced dimensionality. As a consequence, the optical response of non-metallic 2D materials is almost entirely dominated by excitons13. Excitons are usually associated to bound states located within bandgaps. The exciton migration can thus be induced when an ultrashort pulse excites a superposition of those quasi-particle states. In this work, we have performed real-time simulations for monolayer boron nitride (hBN) interacting with an ultrashort UV pulse using our recently developed EDUS approach14. hBN displays two valley pseudospins15,16 related to its inversion symmetry and electronic structure17. We show that the ultrashort pulse enables us to excite a superposition of s- and p- excitons that are localized in different valleys of the reciprocal space (and also different regions in real space). The exciton migration produces the oscillation of excitons from one valley, around the K point, to the other valley, around the K’ point, in about 10 fs (10−15 s). This oscillation is translated into fast beatings in the laser-induced current. Finally, we show that such fast oscillations can be read out by using X-ray attosecond transient absorption spectroscopy (ATAS)1, which has been successfully used to study other electron dynamics processes in insulators18,19,20.

Numerical simulations of ATAS including excitonic effects are challenging. First, because ultrafast schemes require a theory beyond linear response, as one has to describe the absorption of at least two photons (one from the pump pulse, another one from the probe pulse). Second, because valence excitons as those considered in this work can only be described by correctly accounting for the electron-electron interactions. In this respect, some significant progress has been performed at the level of real-time TDDFT21 and real-time Green’s function based methods22, and in our numerical implementation of the semiconductor Bloch equations; EDUS14. In addition, EDUS reduces the computational cost of including core orbitals and enables to describe x-ray interactions. In previous work14, we have shown, by explicit comparison with elaborate calculations for single-photon absorption23,24,25, that a reasonable description of the 2 p and 2 s excitons of hBN can be achieved even at the tight-binding level using a two-band model. Thus, to face the more challenging ATAS scenario, here we have followed a similar approach and used a three-band (two valence + one K-shell) tight-binding model of hBN, see the illustration in Fig. 1a. The core band is flat and belongs to the 1s orbital of N, at an energy of Ech = 410 eV with respect to the Fermi level. Modern laser techniques, based on the nonlinear process of high-harmonic generation (HHG) enables to produce pulses of such energies in the attosecond scale. Experiments have proven to reach those energies, see for example refs. 26,27,28. Also, pump-probe schemes using those pulses have also been demonstrated for few-layers materials8. In brief, we solve the real-time electron dynamics with the EDUS code14,29,30, which consists in evolving the one-electron reduced density matrix in the reciprocal space, see more details in Methods and in the Supplementary Note 1. The laser-matter and electron-electron interactions that give rise to excitonic effects are accounted for on an equal footing in the time domain. Electron-electron interactions are taken into account in the dynamical mean-field approximation, which is a reasonable approximation to describe excitons31. Via the calculated one-electron density matrix in time, we are able then to obtain the polarization of the system and thence the absorption spectrum.

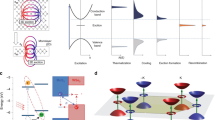
Fig. 1: Producing and reading exciton migration in hBN.
figure 1

a Illustration of the ultrafast scheme and the possible transitions in hBN. b The UV absorption spectrum resulting from our real-time simulations using the EDUS code14. Dashed blue line represents the independent particle approximation (IPA) calculations of the absorption when no electron-electron interactions are included. The peaks correspond to the 1 s, 2 p, and 2 s excitons at 5.32, 6.14, and 6.35 eV, respectively. c–e Distribution in k space for the three excitons, obtained by using a long 120 fs pulse resonant to the corresponding exciton peak and circularly polarized light. f–h The real-space distribution of the three excitons.

Full size image

Results and Discussion

Exciton migration

In our simulations, an 11.3 fs FWHM pulse centered at a photon energy of 6.14 eV and circularly polarized, depicted in Fig. 1a, interacts with hBN. Several exciton peaks are present in the UV spectrum within the bandgap of Eg = 7.25 eV, see Fig. 1b. When electron-electron (excitonic) interactions are switched off, the absorption only takes place for photon energies above the energy bandgap Eg. When excitonic interactions are included, strong absorption peaks appear within the bandgap. The prominent peaks have s- and p- characters, which present a distinctive distribution in k space, see Fig. 1c–e in which the off-diagonal part of the density matrix is represented. The 1s exciton is well-localized around the K points. Note that an opposite handness of the polarization would excite the degenerate 1s exciton that is located at the valley around the K’ point17. The next peak corresponds to the 2 p exciton, which is also degenerate. If we use the same handness for the polarization, then we excite the 2 p exciton, which is mainly localized and shows a clear singularity around the K’ points. This exciton is hybridized with the 2 s exciton32, and shows a small population around the K points. The third peak corresponds to the 2 s exciton, which is also degenerate, and our chosen circular polarization excites the K valleys. Because of the hybridization, this exciton also has a 2p component in the K’ valleys, which is key to induce the exciton migration. By analogy with the charge migration in molecules12, the overlapping of the excited wavefunction states in reciprocal (and real) space makes possible the charge redistribution in time. We represent the three excitons in real space in Fig. 1f–h, see details in Supplementary Note 2. Note that the 2s exciton is well-localized in k space and quite spread in real space. We note that our calculations of the 2p excitons are bright due to the trigonal warping effect, and this is mainly in agreement with other theoretical works32, but there is no reported experimental data to the best of our knowledge.

The ultrashort pulse is broad enough in frequency to excite both the 2 p and 2 s excitons. The laser-induced current in time, see Fig. 2a, presents some quantum beats due to the coherent excitation of the two excitonic states, see the Fourier transform of the current in Fig. 2b. Those quantum beats will last until the coherence is lost. Electron collisions or electron-phonon couplings may contribute to the dephasing, but here we neglect these effects, which will have a minor impact in such short time scale. Also here we note that we use a pump pulse intensity to produce a small exciton density, a 0.2% of electrons in the conduction band, in order to avoid further effects related to a high exciton density. This density is below the critical density for Mott transition33, but it leads to a small energy shift of 0.1 eV. Additional calculations of the effects of the density on the absorption spectra are shown in the Supplementary Note 3. If we plot the time evolution of the density matrix in k space in a maximum of the beating, see Fig. 2c, and in a minimum of the beating, see Fig. 2g, we observe that it mainly moves from the K to the K’ valley in ~10 fs. Then it goes back to its initial state in the next 10 fs. Hence, at some points in time (e.g., 38.5 fs) the exciton is well-localized at the K’ valley, while at other times (e.g., 50 fs) is mainly localized at the K valley. We note that even despite fast current oscillations on frequencies between 6-6.5 eV, the probability distribution of the density matrix in reciprocal and real space oscillates following the quantum beating frequency. The period of the oscillation τ ~ 20 fs is linked to the energy difference ΔE of the exciton states through the formula ΔE = 2π/τ. Therefore, the exciton excitation and energies may be a control knob to tailor the migration oscillations in time. In real space, see Fig. 2d, f, h, we observe how the spatial distribution significantly changes when the exciton is localized around the K valleys and moves to the K’ valleys. The real-space distribution is mainly a linear superposition of the 2 s and 2 p distribution given in Fig. 1d, e. For example, one observes that at t = 38.5 fs the distribution clearly shows the structure of the 2 p, with strong population in the three first neighbors as in the 2s structure. This real-space motion is connected to the calculated beats in the current.

Fig. 2: Exciton migration.
figure 2

a Time evolution of the current induced by the circularly polarized UV pulse. b Fourier transform of the laser-induced current. Two clear frequency modes are observed corresponding to the 2 p and 2 s exciton energies, which form a superposition, while other exciton states are not excited. Figure c–h show snapshots, at the times indicated in (a) of the excitonic distributions in reciprocal and real space.

Full size image

We perform an analysis of the number of electrons that are located at the B and N sites by using the diagonal part of the density matrix in the Wannier gauge14, which corresponds to the population of electrons in the B and N atomic orbitals. After the pump excitation, we have around 0.4% of electrons that move from the N to the B site. From this excited state fraction, around 2% of the electrons oscillate between the B and N sites with the period given by the light-induced exciton migration. This is attributed to the fact that the 2 p-exciton wavefunction have more electrons located around the B site than the 2 s-exciton wavefunction. See more details in the Supplementary Note 4.

Attosecond transient absorption spectroscopy

These results show that coherent population of excitonic states with different degrees of delocalization in the crystal may induce a fast electron/hole motion that controls the current and the valley population in a short time scale. This phenomenon relies on the coherence of the exciton states and therefore it should be observed before the laser-induced coherent dynamics couples to other degrees of freedom. To experimentally observe exciton migration, here we propose to use ATAS. ATAS consists in sending a second laser pulse, the so-called probe pulse, to the system with a certain time delay with respect to the pump pulse, see Fig. 1a, and then in measuring the absorption of the probe pulse as a function of the time delay. In this particular case, we consider an attosecond pulse that excites the K-edge transitions at the nitrogen site, i.e. transitions that promote electrons from the 1 s orbitals of nitrogen to the valence/conduction band. In our tight-binging model we include this additional core band, see more details in the Methods and Supplementary Note 5. The attosecond pulse has a 133-as FWHM duration, and a photon energy centered around 410 eV. The bandwidth of the pulse is large enough to cover all transitions to the valence and conduction bands. With no pump pulse, the calculated absorption shows a prominent core-exciton peak above the Fermi level, see Fig. 3a. This peak arises from the conduction band, as core electrons cannot be promoted into the fully occupied valence band. The transfer of core electrons to the conduction band is clearly illustrated by the relative population of core and conduction bands shown in Fig. 3b. As can be seen, besides the areas around the K,K’ points, the whole reciprocal space is partially populated. This is because the conduction band at those areas is dominated by the 2 p orbitals of boron and we are exciting from the 1s orbital of nitrogen, which is very well-localized in space.

Fig. 3: Laser-induced core excitons.
figure 3

a N K-edge absorption spectrum of the attosecond x-ray pulse in the absence of the pump pulse. Dashed green line represents the IPA calculations of the absorption when no electron-electron interactions are included. Note we take as a reference the energy excitation from the 1 s N orbital to the Fermi level. b Distribution of the population in k space with no pump excitation. c N K-edge absorption spectrum of the attosecond x-ray pulse after pump excitation, the time delay corresponding to the times given in Fig. 2. d, e Distribution in k space for the square modulus of the off-diagonal density matrix of the core-valence part.

Full size image

When the UV pulse is also present, holes created in the valence band through exciton formation can be refilled by N K-shell electrons excited by the attosecond X-ray pulse, leading to distinct peaks appearing below the Fermi level -see scheme in the inset of Fig. 3c. Our real-time simulations show that the shape and magnitude of these peaks are indeed sensitive to exciton migration, see Fig. 3c. The valence band around the K, K’ points is dominated by the 2 p orbitals of nitrogen. This enhances the transitions from the 1 s to the 2 p orbitals of nitrogen. Hence, X-ray excitations are very sensitive to any changes occurring around the reciprocal regions in which the main exciton migration takes place. These excitations can be interpreted as transitions from the 2 s/2 p excitons to the core-excited excitons33,34. Then, by taking the energy difference of those transitions, and knowing also where the quasi-continuum is, we infer that bound core excitons should be located between the -5.4 and -2 eV energy windows of our spectrum. The exciton migration changes the hole distribution in the valence band with time, so that the refilling in the valence band with core electrons will also depend on time, leading to different structures of the core-exciton peaks that are formed. Se more details in Supplementary Note 6. When the 2 p-exciton character is dominant, the valence hole distribution is more extended in the reciprocal space and this enables access to more core exciton states. This is clearly shown in Fig. 3d, e, where we represent the off-diagonal part of the density matrix between the core and valence band in reciprocal space at two different pump-probe delays. As can be seen, the distributions giving rise to core excitons look substantially different at different times.

Finally, we show in Fig. 4 the calculated ATAS during and after the pump excitation. Interestingly, we observe how the population of core excitons significantly increases after the maximum intensity of the pump pulse, following the population of the produced holes in the valence band. Those peaks are around 1% of the intensity of the main core excitons peaks, see Fig. 3a, and appear in an energy window in which there was no absorption of the probe pulse, enabling a high contrast in an experimental measurement. The peaks at −4.0 and −3.4 eV oscillate with the exciton migration, but the most striking feature is found in the energy windows between those peaks, in which we observe the emergence and disappearance of core-exciton peaks. This energy window is ideal for transient absorption measurements in order to read out the fast exciton dynamics and link the absorption peaks to the valence-hole distribution as discussed above.

Fig. 4: Attosecond transient absorption spectroscopy for tracking exciton migration.
figure 4

a Pump pulse in time, b Laser-induced current, and c ATAS features at the valence band. Dashed vertical lines indicate maxima and minima, and intermediate points, of quantum beats in current.

Full size image

Conclusions

In conclusion, we demonstrate the possibility of inducing charge migration in materials whose optical response is dominated by excitons. Using real-time simulations that account both for light-matter and electron-electron interactions, we show how an ultrashort UV pulse induces a superposition of exciton states in hBN that triggers exciton migration between the K and K’ valleys. The migration depends on the exciton energies and laser excitation. Furthermore, we show that this dynamics can be read out by performing X-ray ATAS at the nitrogen K edge, which enables to probe the electron/hole density around individual atomic sites.

In this work we neglect the effects of exciton-phonon interactions, but those are possible to be included in real-time approaches35,36,37,38. We expect the interplay between excitons and phonons to modify the coherence transport, in analogy to charge migration in molecular systems39, and we may even measure these effects using attosecond spectroscopy to study exciton-phonon interactions. Even if coherences are rapidly washed out by nuclear motion, attosecond spectroscopy enables the visualization of these coherences during their brief lifetime.

2D materials offer an ideal platform for controlling the exciton properties via control of layers, substrates, Van der Waals heterostructures, or strain engineering40. Also, exciton energies can be modified by another pulse via laser-induced Stark shift41, and the initial excitation can be tailor using strong-field structured light42. Thus, our study not only advances our understanding of exciton dynamics in attosecond science, but it also opens a promising perspective of exploiting exciton migration for developing transport and valleytronics schemes beyond the strong-field regime41,43,44,45, harnessing ultrafast electronics in two-dimensional materials at the ultimate time scale.

Methods

EDUS implementation

EDUS is a code that enables us to simulate the real-time dynamics of electrons in condensed-matter systems with periodic boundary conditions. It works in reciprocal space and evolves the one-electron density matrix of the system. In particular, the system evolution that is driven out of the equilibrium is described by the reduced, one-particle density matrix

$${\rho }_{nm}({{{{{{{\bf{k}}}}}}}},t)\equiv \langle {\hat{c}}_{m{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }{\hat{c}}_{n{{{{{{{\bf{k}}}}}}}}}\rangle ={{{{{{{\rm{Tr}}}}}}}}[\hat{\varrho }(t){\hat{c}}_{m{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }{\hat{c}}_{n{{{{{{{\bf{k}}}}}}}}}]$$
(1)

where \(\hat{\varrho }(t)\equiv \left\vert \psi (t)\right\rangle \left\langle \psi (t)\right\vert\) is the evolving density operator. The total Hamiltonian of a periodic system is expressed as

$${\hat{H}}_{sys}(t)={\hat{H}}_{0}+{\hat{H}}_{e-e}+{\hat{H}}_{I}(t)$$
(2)

in which \({\hat{H}}_{0}\) contains the non-interacting terms of all electrons, \({\hat{H}}_{e-e}\) accounts for the electron-electron interactions, and \({\hat{H}}_{I}\) is the laser-matter interaction. The latter term depends on the external electric field of the laser pulse and is then time-dependent. EDUS is more efficient working with localized basis, such as Wannier or Gaussian orbitals. The electron-electron interactions can be written in form:

$${\hat{H}}_{e-e}=\frac{1}{2}{\sum}_{\begin{array}{c}n,m,\\ {{{{{{{\bf{k}}}}}}}},{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }\end{array}}{W}_{n{{{{{{{\bf{k+q}}}}}}}}m{{{{{{{\bf{{k}}}}}}}^{{\prime} }-q}},m{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }n{{{{{{{\bf{k}}}}}}}}}{\hat{c}}_{n,{{{{{{{\bf{k+q}}}}}}}}}^{{{{\dagger}}} }{\hat{c}}_{m,{{{{{{{\bf{{k}}}}}}}^{{\prime} }-q}}}^{{{{\dagger}}} }{\hat{c}}_{m,{{{{{{{\bf{{k}}}}}}}^{{\prime} }}}}{\hat{c}}_{n,{{{{{{{\bf{k}}}}}}}}}$$
(3)

where

$$\begin{array}{l}{W}_{m{{{{{{{\bf{k}}}}}}}}l{{{{{{{{\bf{k}}}}}}}}}^{{\prime} },j{{{{{{{{\bf{k}}}}}}}}}_{1}^{{\prime} }n{{{{{{{{\bf{k}}}}}}}}}_{1}}={\iint}_{\!\!\Omega }{d}^{3}r{d}^{3}{r}^{{\prime} }\times \\ {\psi }_{m{{{{{{{\bf{k}}}}}}}}}^{* }({{{{{{{\bf{r}}}}}}}}){\psi }_{l{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }}^{* }({{{{{{{{\bf{r}}}}}}}}}^{{\prime} })V({{{{{{{\bf{r}}}}}}}}-{{{{{{{{\bf{r}}}}}}}}}^{{\prime} }){\psi }_{j{{{{{{{{\bf{k}}}}}}}}}_{1}^{{\prime} }}({{{{{{{{\bf{r}}}}}}}}}^{{\prime} }){\psi }_{n{{{{{{{{\bf{k}}}}}}}}}_{1}}({{{{{{{\bf{r}}}}}}}}).\end{array}$$
(4)

Two-particle interaction Hamiltonian is approximated by a Hartree-Fock mean-field potential that can be written as:

$${\hat{H}}_{e-e}\approx {\hat{H}}_{e-e}^{{{{{{{{\rm{Fock}}}}}}}}}+{\hat{H}}_{e-e}^{{{{{{{{\rm{Hartree}}}}}}}}}= -{\sum}_{\begin{array}{c}m,n,\\ {{{{{{{{\bf{k,k}}}}}}}}}^{{\prime} },{{{{{{{\bf{G}}}}}}}}\end{array}}{e}^{i({{{{{{{{\bf{k}}}}}}}}}^{{\prime} }-{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{G}}}}}}}})\cdot ({{{{{{{{\bf{t}}}}}}}}}_{m}-{{{{{{{{\bf{t}}}}}}}}}_{n})}{V}_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }+{{{{{{{\bf{G}}}}}}}}}\ {\rho }_{mn}^{(B)}({{{{{{{{\bf{k}}}}}}}}}^{{\prime} },t){\hat{c}}_{m,{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }\ {\hat{c}}_{n,{{{{{{{\bf{k}}}}}}}}}\\ +{\sum}_{\begin{array}{c}m,n,\\ {{{{{{{{\bf{k,k}}}}}}}}}^{{\prime} },{{{{{{{\bf{G}}}}}}}}\ne 0\end{array}}\Re {e}^{i{{{{{{{\bf{G}}}}}}}}({{{{{{{{\bf{t}}}}}}}}}_{m}-{{{{{{{{\bf{t}}}}}}}}}_{n})}{V}_{{{{{{{{\bf{G}}}}}}}}}\ {\rho }_{mm}^{(B)}({{{{{{{{\bf{k}}}}}}}}}^{{\prime} },t){\hat{c}}_{n,{{{{{{{\bf{k}}}}}}}}}^{{{{\dagger}}} }\ {\hat{c}}_{n,{{{{{{{\bf{k}}}}}}}}}.$$
(5)

Where \({\rho }_{nm}^{(B)}({{{{{{{{\bf{k}}}}}}}}}^{{\prime} },t)\) is a time-dependent density matrix in a localized basis, tm is the position of the atom where the orbital is localized, Vk is the Fourier transform of the Coulomb energy V(r), G − reciprocal-lattice vectors.

The light-matter interaction term is written in the so-called length gauge \({\hat{H}}_{I}(t)=| e| {{{{{{{\boldsymbol{\varepsilon }}}}}}}}(t)\cdot \hat{{{{{{{{\bf{r}}}}}}}}}\), where \(\hat{{{{{{{{\bf{r}}}}}}}}}\) represents the position operator of the electrons in the system and ε(t) is the electric field of the laser pulse. This particular form is only valid in the dipole approximation, and for Bloch basis it is cast as

$$\hat{{{{{{{{\bf{r}}}}}}}}}={\sum}_{\begin{array}{c}{{{{{{{{\bf{k}}}}}}}}}^{{\prime} },{{{{{{{\bf{k}}}}}}}}\\ n,m\end{array}}[{\xi }_{nm}({{{{{{{\bf{k}}}}}}}})\delta ({{{{{{{\bf{k}}}}}}}}-{{{{{{{{\bf{k}}}}}}}}}^{{\prime} })-i{\delta }_{nm}{{{{{{{{\boldsymbol{\nabla }}}}}}}}}_{{{{{{{{\bf{k}}}}}}}}}\delta ({{{{{{{\bf{k}}}}}}}}-{{{{{{{{\bf{k}}}}}}}}}^{{\prime} })]{c}_{n{{{{{{{{\bf{k}}}}}}}}}^{{\prime} }}^{{{{\dagger}}} }{c}_{m{{{{{{{\bf{k}}}}}}}}}$$
(6)

Finally, the equation of motion to solve is

$$i\hslash \frac{\partial {\rho }_{nm}({{{{{{{\bf{k}}}}}}}},t)}{\partial t}=\, i\hslash \frac{\partial {\rho }_{nm}({{{{{{{\bf{k}}}}}}}},t)}{\partial t}{| }_{deph}\\ +{\left[{H}_{0}({{{{{{{\bf{k}}}}}}}})+{H}_{e-e}({{{{{{{\bf{k}}}}}}}})+| e| {{{{{{{\boldsymbol{\varepsilon }}}}}}}}(t)\cdot {{{{{{{\boldsymbol{\xi }}}}}}}}({{{{{{{\bf{k}}}}}}}}),\rho ({{{{{{{\bf{k}}}}}}}},t)\right]}_{nm}\\ +i| e| {{{{{{{\boldsymbol{\varepsilon }}}}}}}}(t)\cdot {\nabla }_{{{{{{{{\bf{k}}}}}}}}}\,{\rho }_{nm}({{{{{{{\bf{k}}}}}}}},t)$$
(7)

All electron correlations beyond the mean field approximation are included in the term iℏ∂ρnm(k, t)/∂t∣deph. Here we include the core-hole decay mainly dominated by Auger processes as iℏ∂ρnm(k, t)/∂t∣deph = − Γρnm(k, t), where Γ = 4 × 10−3  a.u.

Core tight-binding for hBN

We use a tight-binding model for describing hBN, which consists in including the 2 p orbitals of boron and nitrogen that are perpendicular to the monolayer and mainly contribute to the valence/conduction bands. The Hamiltonian in the reciprocal space can be expressed as:

$${\hat{H}}_{f}({{{{{{{\bf{k}}}}}}}})={\sum }_{i=1}^{3}{B}_{i}({{{{{{{\bf{k}}}}}}}}){\hat{\sigma }}_{i},$$
(8)

where we use the Pauli matrices, and \({B}_{1}({{{{{{{\bf{k}}}}}}}})=\gamma {\sum }_{i}\cos \left({{{{{{{\bf{k}}}}}}}}\cdot {\delta }_{i}\right)\), \({B}_{2}({{{{{{{\bf{k}}}}}}}})=\gamma {\sum }_{i}\sin \left({{{{{{{\bf{k}}}}}}}}\cdot {\delta }_{i}\right)\), and \({B}_{3}({{{{{{{\bf{k}}}}}}}})=\frac{\Delta }{2}\), while γ is the first-order hopping and Δ is the bandgap energy. In our case γ = 2.3 eV, Δ = 7.25 eV, the lattice vectors δ = (2.17, ± 1.25)Å, and the lattice parameter a = 2.5Å. Note we work in the lattice gauge of a tight-binding model.

For Coulomb interaction we used the Rytova-Keldysh potential

$${V}_{{{{{{{{\bf{q}}}}}}}}}^{(RK)}=\frac{{e}^{2}}{{\epsilon }_{0}({\epsilon }_{1}+{\epsilon }_{2})A}\frac{1}{| {{{{{{{\bf{q}}}}}}}}| \left({r}_{0}| {{{{{{{\bf{q}}}}}}}}| +1\right)}$$
(9)

Here A is the area of the unit cell. The parameters are chosen to be ϵ1 = ϵ2 = 1, representing monolayer hBN in vacuum, and r0 = 10 Å, taken from previous DFT works23,24.

We need to include core orbitals in order to describe the x-ray interactions in the ultrafast spectroscopy scheme. We add the 1s orbital of boron or nitrogen at the previous model. The extended Hamiltonian can be written as

(10)

where Hij are the elements of the Hamiltonian given by Eq. (8), where E1s and Ef are the 1s orbital and the Fermi energy, respectively. In this core tight-binding model with three basis \(\left\{{\Phi }_{1s},\,{\Phi }_{2pB},\,{\Phi }_{2pN}\right\}\), the Berry connection is then written as

$${\xi }^{(w)}=\left(\begin{array}{ccc}0&0&{{{{{{{{\bf{r}}}}}}}}}_{1s,2p}\\ 0&{{{{{{{{\bf{r}}}}}}}}}_{c}&0\\ {{{{{{{{\bf{r}}}}}}}}}_{1s,2p}&0&0\end{array}\right)$$
(11)

where r1s,2p is the Berry connection between the 1s and 2 p orbital of nitrogen, calculated as the matrix element of the position operator between corresponding orbital wave functions on the same site. In the case of studying the boron K-edge absorption, then we need to change these elements in the matrix accordingly. rc is the position of the boron atom, we take as the origin of the nitrogen site. Here we work in the lattice gauge, in the atomic gauge all elements of the diagonal part of the Berry connection is zero.

Light-matter interactions

In the light-matter interaction term, we can include any laser pulse in time, in which the electric field ε(t) needs to be specified. We emphasize that we are not limited to the linear response regime. In order to include two pulses, we can just add the sum of both in the interaction term and change the time delay accordingly, i.e. ε(t) = εp(t) + εx(t), where εp and εx is the electric field of the pump and probe pulse. The pump pulse has a photon energy comprised between 5 and 7 eV in the UV regime and is circularly polarized.

The spectrum on Fig. 1 b in the main text is calculated by simulation of the broad pulse of duration 5 fs centered on frequency 6 eV, a peak intensity of 107  W/cm2. Isolated excitons (Fig. 1c–e) were obtained by long circularly polarized pulse of sin2 shape, 45 fs FWHM duration, and peak intensity 106  W/cm2.

The pulse that generates the exciton migration has a 11.3 fs FWHM pulse length and a peak intensity of 1010  W/cm2. The shape of the pulse is modeled by a sin2 function. The probe pulse has a photon energy of around 410 eV in the X-ray regime and is linearly polarized. For the ultrafast scheme, it is considered a 133 as FWHM pulse length and a peak intensity of 107  W/cm2. The shape of the pulse is modeled by a Gaussian function.

In order to obtain Fig. 4c we modeled a set of absorptions of XUV pulses, changing the center of the probe pulse with a step of 0.25 fs.