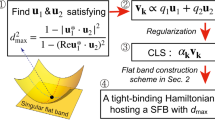
Abstract
The localized nature of a flat band is understood by the existence of a compact localized eigenstate. However, the localization properties of a partially flat band, ubiquitous in surface modes of topological semimetals, have been unknown. We show that the partially flat band is characterized by a non-normalizable quasi-compact localized state (Q-CLS), which is compactly localized along several directions but extended in at least one direction. The partially flat band develops at momenta where normalizable Bloch wave functions can be obtained from a linear combination of the non-normalizable Q-CLSs. Outside this momentum region, a ghost flat band, unseen from the band structure, is introduced based on a counting argument. Then, we demonstrate that the Wannier function corresponding to the partially flat band exhibits an algebraic decay behavior. Namely, one can have the Wannier obstruction in a band with a vanishing Chern number if it is partially flat. Finally, we develop the construction scheme of a tight-binding model for a topological semimetal by designing a Q-CLS.
Similar content being viewed by others
Introduction
Flat bands have received significant attention because they are considered an ideal playground to study many-body physics1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23 and geometric properties of the Bloch wave function beyond topological aspects24,25,26,27,28,29,30,31,32,33. While it has long been believed that the flat band can only be realized in artificial systems34,35,36,37,38,39,40, including the Aharonov-Bohm cage with the two-band Creutz ladder and the three-band rhombic lattice41,42,43,44,45, there has recently been a surge of research on synthesizing flat band materials46,47,48,49,50,51 after discovering the unconventional superconductivity originating from the flat band in the twisted bilayer graphene52. As a result, flat band materials are now regarded as intriguing quantum materials with promising implications, attracting interest from both fundamental and application-oriented perspectives.
The localization of charge carriers in a flat band, essential for understanding many-body phenomena in the system, has an intriguing origin. Suppose a flat band is perfectly dispersionless over the whole Brillouin zone, denoted by a fully flat band. The localization nature of the full flat band is understood by the existence of a special eigenmode called a compact localized state(CLS)53,54,55,56. The amplitude of the CLS is nonzero only inside a finite region while completely vanishing outside of it. The CLS can be stabilized due to the destructive interference provided by the flat band system’s specific lattice and hopping structures. This explains how the electrons can be localized in the flat band systems, although electrons are itinerant via the hopping processes. Moreover, it was shown that when the flat band’s Bloch eigenfunction possesses a singularity due to a band-crossing, one cannot find a set of independent CLS spanning the flat band. In this case, several extended states, called the non-contractible loop states, should be added to the set to achieve completeness53,54. Non-contractible loop states exhibit exotic real-space topology probed in photonic lattices37. From designing CLSs and non-contractible loop states, one can also easily construct flat band tight-binding models57.
Besides the full flat band, one can also observe partially flat bands frequently on the edge or surface of topological semimetals, such as graphene and nodal line semimetals58,59,60,61,62,63,64. In the zigzag graphene nanoribbon, we have partially flat bands between two Dirac points. In fact, they are nearly flat bands with momentum dependence ~ (k−π)Q around the zone boundary, where Q is the number of dimer lines proportional to the ribbon width. In the semi-infinite limit(Q → ∞), the exact partially flat band is realized. The partially flat bands of the zigzag graphene nanoribbon attracted tremendous attention due to their instability toward the half-metallic ground state65. Another well-known example is the drum-head surface states of nodal-line semimetals61,62,63,64, which are expected to lead to the high-temperature superconductivity66.
This paper answers the question of how to understand the localization nature of partially flat bands. In the case of the full flat band, one can always find N(the number of unit cells in the system) CLSs spanning the flat band completely if the flat band has no singularity54. This property characterizes the localization nature of the full flat band54,55,67. The same idea may not be applied to the partially flat band because it has only fN degenerate Bloch states, where f is a fractional number(0 < f < 1) representing the ratio between the flat region and the Brillouin zone. However, N number of different CLSs must exist if at least one CLS is found, by moving the center of the CLS to different unit cells. This macroscopic mismatch between the number of Bloch wave functions and CLSs implies that the conventional CLS cannot exist in the partially flat band.
We demonstrate that the partially flat band is characterized by an unconventional type of CLS called a quasi-compact localized state(Q-CLS). Note that the Q-CLS is non-normalizable. With a normalizable regular localized eigenstate, one can find N independent such states by translated copies of them. Then, their Bloch summations with different crystal momenta give N independent Bloch states, which correspond to a full flat band, not a partially flat band. The partially flat bands are usually found in semi-infinite systems, where the normalizability condition can be broken. The Q-CLS shows the compactly localized feature along the translationally invariant direction. However, its amplitude can grow away from the boundary, resulting in a non-normalizable state. Although it does not make sense to use the non-normalizable states conventionally, we note that their Bloch sums can be normalizable depending on the crystal momentum. The partially flat band appears in the momentum range with normalizable Bloch sums of Q-CLSs, while we propose that there is a ghost flat band outside this range because the corresponding Bloch states cannot be normalized. The unphysical, non-normalizable states cannot be observed in a spectroscopy. However, introducing the ghost flat band can resolve the frustrated counting argument because we have the same number of Bloch states(from both the partially flat band and ghost flat band) and the Q-CLSs. We also investigate the localization properties of the Wannier functions of the partially flat band. The exponential decay of the Wannier function of an isolated analytic band explains the localization nature of insulators68,69. This Wannierization is obstructed in topological bands due to the singular properties of the corresponding Bloch wave function70. We show that the Wannier obstruction can also occur in a topologically trivial band if it is a partially flat band because the Bloch wave functions in the ghost flat band do not participate in the construction of the Wannier functions. In the partially flat band, the Wannier function exhibits 1/r1+ϵ and 1/r3/2+ϵ decays with a positive number ϵ in 1D and 2D, respectively, instead of the exponential one. Finally, we develop a systematic scheme for constructing a tight-binding Hamiltonian hosting a partially flat band by designing an Q-CLS. Since the partially flat bands are usually the surface modes of topological semimetals, this scheme can be used to obtain topological semimetal models.
Results
Non-normalizable compact localized states
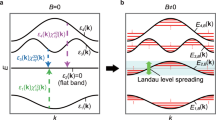
We discuss the generic localization nature of a partially flat band by considering a specific example, the partially flat band of a semi-infinite graphene with a zigzag edge, illustrated in Fig. 1(a). As denoted in Fig. 1(b), positions of A and B sites are represented by RA(m, n) = ma1 + na2 and RB(m, n) = ma1 + na2 + b, respectively, where \({{{{{{{{\bf{a}}}}}}}}}_{1}=a(\sqrt{3}/2,-1/2)\), a2 = a(0, 1), and \({{{{{{{\bf{b}}}}}}}}=(a/\sqrt{3})(1/2,\sqrt{3}/2)\). Here, m≥0 is the dimer line index, and a is the lattice constant. The dimer line indicates the zigzag chain of carbon atoms along y-direction in graphene. The dimer line index m is assumed to increase away from the system’s boundary starting from m = 0. Here, only the nearest neighbor hopping processes are included. We look for a CLS localized along the translationally invariant direction, namely y-axis in Fig. 1(b). One can find a zero energy eigenstate, illustrated in Fig. 1(b), whose amplitudes at A sites are given by
where n*a2 is the position of the left-end vertex of this state, as indicated by an arrow in Fig. 1(b). Here, mCn = m!/n!(m − n)! is the binomial coefficient. The amplitudes at B sites, denoted by \({\phi }_{{n}^{* }}^{{{{{{{{\rm{B}}}}}}}}}(m,n)\), are zero. This solution is found by following steps. First, assign an amplitude 1 at an A site at the boundary (m = 0). Then, we find amplitudes at A sites in the next dimer line (m = 1) so that the amplitudes of the wave function resulting from the hopping processes become zero at B sites in the m = 0 dimer line. We repeat the same procedure increasing m. We set the amplitudes at B sites identically zero to obtain a zero-energy solution. In total, the eigenstate is written as \(\left\vert {\phi }_{{n}^{* }}\right\rangle ={\sum }_{m,n}[{\phi }_{{n}^{* }}^{{{{{{{{\rm{A}}}}}}}}}(m,n){a}_{m,n}^{{{{\dagger}}} }+{\phi }_{{n}^{* }}^{{{{{{{{\rm{B}}}}}}}}}(m,n){b}_{m,n}^{{{{\dagger}}} }]\left\vert 0\right\rangle\), where \({a}_{m,n}^{{{{\dagger}}} }\)(\({b}_{m,n}^{{{{\dagger}}} }\)) creates an electron at A(B) site with position RA(m, n)(RB(m, n)). The compactly localized feature of this state is due to the destructive interference between \({\phi }_{{n}^{* }}^{{{{{{{{\rm{A}}}}}}}}}(m,{n}^{* })\)(\({\phi }_{{n}^{* }}^{{{{{{{{\rm{A}}}}}}}}}(m,{n}^{* }+m)\)) and \({\phi }_{{n}^{* }}^{{{{{{{{\rm{A}}}}}}}}}(m+1,{n}^{* })\)(\({\phi }_{{n}^{* }}^{{{{{{{{\rm{A}}}}}}}}}(m+1,{n}^{* }+m)\)) at the neighboring B site after the hopping processes. However, this is a non-normalizable state since the amplitudes grow as the dimer line index m increases. This is the Q-CLS described in the introduction. There are N degenerate Q-CLSs at zero energy depending on the vertex position n*, where N is the number of unit cells along the y-axis. Since the left-end vertices of the N Q-CLSs with different n*’s do not overlap, the N Q-CLSs are independent of each other even within the periodic boundary condition along y-axis.
a The band structure of a semi-infinite zigzag graphene nanoribbon. At zero energy, the partially flat band and ghost flat band are plotted by the red solid and gray dashed lines, respectively. b The semi-infinite zigzag graphene nanoribbon has an edge on the left-hand side. The quasi-compact localized state(Q-CLS) is drawn by a gray region. The amplitudes of the Q-CLS are denoted by the colored circles, whose size stands for the magnitude of the amplitude, while the color represents the sign. We have different Q-CLSs depending on the position of the vertex indicated by the red star symbol. c A linear combination of the Q-CLSs, resulting in a Bloch wave function, whose amplitudes are plotted in (d).
We show that a normalizable Bloch eigenstate can be obtained from a linear combination of the Q-CLSs, as illustrated in Fig. 1c. We build an extended eigenstate satisfying the Bloch theorem given by
whose amplitude reads
for the A sites at RA(m, n) while \({\psi }_{k}^{{{{{{{{\rm{B}}}}}}}}}(m,n)=0\), as plotted in Fig. 1d. The eigenenergy corresponding to this mode is zero because that of \(\left\vert {\phi }_{{n}^{* }}\right\rangle\) is zero. Most importantly, the obtained Bloch eigenstate shows exponential decay along a2 direction if k ∈ IL = ( − π, − 2π/3) or k ∈ IR = (2π/3, π). Here, the Brillouin zone is set to be − π < k ≤ π. Namely, \(\left\vert {\psi }_{k}\right\rangle\) is a normalizable one-dimensional Bloch wave function for momenta belonging to IL or IR. Outside these two intervals, on the other hand, the constructed Bloch states should be discarded and invisible in spectroscopy because they cannot be normalized. Therefore, we have zero energy flat band in IL and IR, which realizes the partially flat band. This partially flat band is not connected to other bands and is terminated in the middle of the Brillouin zone. Meanwhile, one can consider the zero energy states corresponding to the non-normalizable \(\left\vert {\psi }_{k}\right\rangle\) outside IL and IR as a ghost flat band. We have in total N number of states in the partially flat band and ghost flat band, which is consistent with the N number of independent Q-CLSs \(\left\vert {\phi }_{{n}^{* }}\right\rangle\).
In general, we conjecture that a partially flat band is obtained in a semi-infinite system by discarding the ghost part of a full flat band. A semi-infinite system is a good playground to have such a ghost band for the following reasons. Considering only hermitian tight-binding Hamiltonians, which can be block-diagonalizable into the finite-size Bloch Hamiltonians, the bulk’s band dispersion should be analytic in momentum because every matrix element of the Bloch Hamiltonian of such a model is analytic in momentum space. However, the partially flat band cannot be an analytic function of momentum because an integer n exists such that the n-th left- and right-hand derivative of the band becomes discontinuous at the end-point of the partially flat band. Therefore, the flat band should always be a full flat band in such a conventional Hamiltonian. One of the ways to violate the properties of the conventional Hamiltonians is to make the size of the Bloch Hamiltonian infinite, which is impossible in reality in principle. The semi-infinite systems are the examples, and the non-normalizable states can emerge in such systems, as shown in the example above.
We apply our general conclusions to a 3D topological nodal-line semimetal. We consider the minimal tight-binding Hamiltonian on a cubic lattice given by \({H}_{{{{{{{{\rm{NL}}}}}}}}}=\sin {k}_{z}{\sigma }_{y}+(2-\cos {k}_{x}-\cos {k}_{y}-\cos {k}_{z}){\sigma }_{z}\), where σα is a Pauli matrix representing the orbital degree of freedom for each site. We denote two orbitals by ξ = ± . The hopping structure is illustrated in Fig. 2a. Lattice sites are represented by R(n) = nxax + nyay + nzaz, where aα is a unit vector along α-direction. This model hosts a nodal ring described by \(1=\cos {k}_{x}+\cos {k}_{y}\) at zero energy, as plotted in Fig. 2b. When the system is terminated along z-direction, we have a drumhead flat surface mode inside the nodal ring. We consider a semi-infinite system obtained by removing sites with a negative nz in the cubic lattice. The quasi-localized feature of this drumhead partially flat band is explained by a zero energy Q-CLS illustrated in Fig. 2c, whose apex is located at \({{{{{{{\bf{R}}}}}}}}({{{{{{{{\bf{n}}}}}}}}}^{* })={n}_{x}^{* }{{{{{{{{\bf{a}}}}}}}}}_{x}+{n}_{y}^{* }{{{{{{{{\bf{a}}}}}}}}}_{y}\). Denoting the Q-CLS by \(\left\vert {\phi }_{{{{{{{{{\bf{n}}}}}}}}}^{* }}\right\rangle\), its amplitude for the ξ-orbital at R(n) is the coefficient of the exponential factor \({e}^{i({n}_{x}-{n}_{x}^{* }){k}_{x}+i({n}_{y}-{n}_{y}){k}_{y}}\) of a function given by
where β = x and y. Detailed derivations are included in Supplementary Notes 1. Since the above formula is a finite polynomial of the exponential factors, \({\phi }_{{{{{{{{{\bf{n}}}}}}}}}^{* },\xi }({{{{{{{\bf{n}}}}}}}})\) is nonzero only inside a finite region for a given nz, which implies the compact localization. Then, by a linear combination of the Q-CLSs (Fig. 2d), we obtain Bloch eigenfunction, \(\left\vert {\psi }_{{{{{{{{\bf{k}}}}}}}}}\right\rangle ={\sum }_{{{{{{{{{\bf{n}}}}}}}}}^{* }}{e}^{i{{{{{{{{\bf{n}}}}}}}}}^{* }\cdot {{{{{{{\bf{k}}}}}}}}}\left\vert {\phi }_{{{{{{{{{\bf{n}}}}}}}}}^{* }}\right\rangle\), whose amplitudes are evaluated as
where k = (kx, ky). The Bloch wave function exhibits exponential decay and can be normalized in a momentum range \(-1 < 2-\cos {k}_{x}-\cos {k}_{y} < 1\), precisely the same as the drum-head surface mode’s region above. Outside the nodal ring, the constructed Bloch wave function increases exponentially as a function of nz and cannot be normalized, which leads to the ghost flat band.
a The lattice and hopping structures of the 3D nodal line semimetal model. At each site, two orbitals, denoted by A and B, reside. Lines with red, blue, and yellow colors represent hopping processes. Solid and dashed lines indicate + and − signs of the hopping amplitudes. (b) The band structure for kz = 0. The nodal ring is denoted by the red closed curve. (c) A schematic view of the quasi-compact localized state(Q-CLS) of the nodal line semimetal in the semi-infinite system. (d) A linear combination of Q-CLSs in (c) with different apex positions, resulting in a Bloch wave function.
Wannier obstruction
The localization nature of an insulator is explained by exponentially decaying Wannier functions69. According to the Paley-Wiener theorem, such states are guaranteed to exist if the Bloch wavefunctions are analytic over the whole Brillouin zone71. Bloch wavefunctions are always analytic in 1D, and one can find exponentially localized Wannier functions in a 1D isolated band. On the other hand, in 2D, a topologically nontrivial band cannot have such a Wannierization due to singularities of the corresponding Bloch eigenfunction in momentum space. Here, we investigate the Wannier function properties of a partially flat band, where one cannot apply the Paley-Wiener theorem because the Fourier transform of the Bloch wave function is ill-defined due to the absence of the wave function outside the partially flat band regions in the Brillouin zone.
Let us begin with the 1D partially flat band of a semi-infinite system. A general form of the Bloch wave function of the partially flat band is given by
where n is the unit cell index along the translationally invariant direction, m is the sublattice index, and σm represents the orbital in the m-th sublattice. Here, m increases as we go away from the semi-infinite system’s boundary(m = 0). The semi-infinity is described by the limit process Q → ∞. We assume that there are Pm orbitals in the m-th sublattice. Finally, \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\) is the component corresponding to the σm-th orbital in the m-th sublattice of the partially flat band’s eigenvector v(Q)(k) of the Bloch Hamiltonian. Here, v(Q)(k) is obtained by holding the components of the unnormalized Bloch wave function constructed from the Q-CLSs, such as (3), up to the Q-th sublattice and normalizing it. For example, for the semi-infinite graphene, we have \({v}_{m}^{(Q)}(k)={\psi }_{k}^{{{{{{{{\rm{A}}}}}}}}}(m,0)/{(\sum \nolimits_{{m}^{{\prime} } = 0}^{Q}| {\psi }_{k}^{{{{{{{{\rm{A}}}}}}}}}({m}^{{\prime} },0){| }^{2})}^{1/2}\). Note that, before reflecting the semi-infinity(Q → ∞) of the system, \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\) is analytic over the whole Brillouin zone, even out of the partially flat band region. As a result, the Fourier transform of \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\) exponentially decays far from the Wannier center according to the Paley-Wienener theorem and we have \({v}_{m,{\sigma }_{m}}^{(Q)}(k)=(1/\sqrt{N}){\sum }_{n}{e}^{ikn}{\varphi }_{m,{\sigma }_{m}}^{(Q)}(n)\), where \({\varphi }_{m,{\sigma }_{m}}^{(Q)}(n) \sim {e}^{-b| n| }\) for ∣n∣ → ∞ with a positive coefficient b. Now, we obtain the Wannier function for the partially flat band by using this form of \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\) in the semi-infinite limit(Q → ∞). In this limit, \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\) is ill-defined for momenta corresponding to the ghost flat band. Therefore, performing the integral over the momentum range corresponding to the partially flat band is natural to construct a Wannier function from \({v}_{m,{\sigma }_{m}}^{(Q)}(k)\). Then, the Wannier function amplitude for the σm-th orbital is given by
where BZ represents the Brillouin zone and n0 is the Wannier function’s center. Let us denote Δn = n − n0, \({v}_{m,{\sigma }_{m}}(k)={\lim }_{Q\to \infty }{v}_{m,{\sigma }_{m}}^{(Q)}(k)\), and \({\varphi }_{m,{\sigma }_{m}}(k)={\lim }_{Q\to \infty }{\varphi }_{m,{\sigma }_{m}}^{(Q)}(k)\). In this semi-infinite limit, the integration range in momentum space is reduced to an interval IPFB, where the partially flat band resides. IPFB is generally an union of many sub-intervals, where the l-th one is [kl,i, kl,f]. Then, the continuum limit of the momentum summation above is given by
Performing the momentum integration, we obtain
where
and sα = − 1 or 1 for α = i or f, respectively. Detailed derivations are included in Supplementary Note 2. Since we are interested in the behavior of W(Δn) in the limit ∣Δn∣ → ∞, let us consider a function \({\tilde{F}}_{l,m,{\sigma }_{m}}(x)={F}_{l,m,{\sigma }_{m}}(1/x)\), where x = 1/Δn. One can show that \({\tilde{F}}_{l,m,{\sigma }_{m}}(0)=0\) because the eigenvector component \({v}_{m,{\sigma }_{m}}(k)\) should be zero at kl,i and kl,f, boundaries of the partially flat band to be continuously connected to the eigenvector component of the ghost flat band, which is zero in the limit Q → ∞. To figure out the functional form of \({\tilde{F}}_{l,m,{\sigma }_{m}}(x)\) near x = 0, we consider an arbitrary order of derivatives of it at x = 0. We evaluate \({\partial }_{x}^{p}{\tilde{F}}_{l,m,{\sigma }_{m}}(x){| }_{x = 0}\) and denote the smallest p, where the derivative becomes nonzero, by p*. If \(| {\partial }_{x}^{p}{\tilde{F}}_{l,m,{\sigma }_{m}}(x){| }_{x = 0}| < \infty\) for p ≥ p*, one can deduce that \({\tilde{F}}_{l,m,{\sigma }_{m}}(x) \sim {x}^{{p}^{* }}\). This implies that \({W}_{m,{\sigma }_{m}} \sim 1/{r}^{1+{p}^{* }}\) from (10). On the other hand, \({\partial }_{x}^{{p}^{* }}{\tilde{F}}_{l,m,{\sigma }_{m}}(x){| }_{x = 0}\) can be divergent too. In this case, one can infer that \({\tilde{F}}_{l,m,{\sigma }_{m}}(x)\) is an irrational function of the form xϵ, where p* − 1 < ϵ < p* because \({\tilde{F}}_{l,m,{\sigma }_{m}}(x)\) vanishes at x = 0. In this case, we have \({W}_{m,{\sigma }_{m}} \sim 1/{r}^{1+\epsilon }\). In total, the Wannier function decays algebraically as ~ 1/r1+ϵ, where p* − 1 < ν ≤ p*. Note that the Wannier functions with different n0 of the partially flat band are not orthogonal to each other in general because not all the Bloch wave functions in the Brillouin zone participate in constructing the Wannier functions. As a result, while there can be N different Wannier functions with distinct n0 values, only N∑l(kl,f − kl,i)/2π number of them are independent of each other. Similar conclusions to the 1D Wannierization above can be applied to the two-dimensional partially flat bands. Specifically, we show that the Wannier function corresponding to the 2D partially flat band exhibits 1/r3/2+ϵ decay far from its center, where ϵ is a positive number. Detailed derivations are included in Supplementary Notes 3.
Let us consider semi-infinite graphene as an example. Using (3), we have the normalized eigenvector component of the partially flat band, evaluated as \({v}_{m}(k)={\lim }_{Q\to \infty }{v}_{m}^{(Q)}(k)={[1-4{\cos }^{2}(k/2)]}^{1/2}{(1+{e}^{-ik})}^{m}\), where the orbital index σm is dropped because we have only one orbital per sublattice. The momentum range for the partially flat band is given by IPFB = [2π/3, 4π/3]. Outside the partially flat band region, vm(k) = 0. The Wannier function is obtained by \({W}_{m}(n-{n}_{0})=(1/2\pi )\int\nolimits_{2\pi /3}^{4\pi /3}dk\,{v}_{m}(k){e}^{ik(n-{n}_{0})}\) for the m-th dimer line. When n0 = 0, the Wannier function amplitudes for several values of m are plotted in Fig. 3(a). We note that Wm(n) ~ 1/n3/2 for large n as shown in the inset of Fig. 3(a). This is consistent with that ∂kvm(k) diverges at k = 2π/3 and 4π/3. This implies that the Wannier function of the semi-infinite graphene with a zigzag edge decays algebraically( ~ 1/r3/2) along the translationally invariant direction. In the case of the semi-infinite nodal line semimetal described by HNL above, the normalized eigenvector’s component of the partially flat band corresponding to the nz-th layer from the surface is given by \({v}_{{m}_{z}}({{{{{{{\bf{k}}}}}}}})={\lim }_{Q\to \infty }{v}_{{m}_{z}}^{(Q)}({{{{{{{\bf{k}}}}}}}})={[(\cos {k}_{x}+\cos {k}_{y}-1)(3-\cos {k}_{x}-\cos {k}_{y})]}^{1/2}{(2-\cos {k}_{x}-\cos {k}_{y})}^{{n}_{z}}\) inside the nodal ring. Outside the nodal ring, \({\lim }_{Q\to \infty }{v}_{{m}_{z}}^{(Q)}({{{{{{{\bf{k}}}}}}}})=0\). By using it, we obtain the Wannier function for the partially flat band and observe another algebraic decay proportional to 1/r2 along various directions on the surface, as plotted in Fig. 3(b). This is consistent with the generic 1/r3/2+ϵ decay of the 2D partially flat band’s Wannier function shown above. The results reveal another origin of the Wannier obstruction for a band with the vanishing Chern number. While the partially flat band belongs to a full flat band, it was shown rigorously that the Chern number of a full flat band is always zero.
a, b Plot the Wannier function amplitudes of the semi-infinite zigzag graphene nanoribbon and nodal line semimetal, respectively. m and mz represent the dimer lines and layers away from the edge and surface of these two systems. n is an index of the unit cell along a translationally invariant direction. In the insets, we show that the local maxima of the Wannier functions decay algebraically. c A band dispersion of a finite-width zigzag graphene nanoribbon. The red and blue bands in the middle correspond to the edge states. d The Wannier function for the red band in (c) for various values of m. In (a), (b), and (d), the dashed curves are the guide lines showing the algebraic decay of the Wannier functions, obtained by fitting the local maxima of them.
Construction of topological semimetal models
By reversely using the fact that the eigenvector’s components of the partially flat band are in the form of the polynomial of exponential factors, one can find a topological semimetal model. The general procedure is as follows. (i) For a semi-infinite lattice structure, assign a proper index (denoted by m) for the orbitals in it, increasing away from the boundary. (ii) Design an unnormalized eigenvector of infinite size (vPFB(k)) for an expected partially flat band at the zero energy. The components of vPFB(k) are in the form of f(k)m, where f(k) is a sum of exponential factors eik⋅n. (iii) Construct an infinite-size Hamiltonian HSI matrix satisfying the eigenvalue equation HSIvPFB = 0. Here we assume that every element of HSI is a sum of eik⋅n reflecting the finite hopping range. We expect the Dirac points to appear at momenta with ∣f(k)∣ = 1. (iv) Transform the Hamiltonian of the semi-infinite system HSI into a Hamiltonian for a bulk system without boundaries. This can be done by extracting hopping processes of HSI in real space away from the boundary.
Let us obtain a topological semimetal in a square lattice by applying the above scheme. We consider a 2D semi-infinite rectangular lattice consisting of two sublattices denoted by A and B and translationally invariant along x direction. We arrange the partially flat band’s eigenvector component as \({{{{{{{\bf{v}}}}}}}}(k)={({v}_{1{{{{{{{\rm{A}}}}}}}}}(k),{v}_{1{{{{{{{\rm{B}}}}}}}}}(k),\cdots ,{v}_{m{{{{{{{\rm{A}}}}}}}}}(k),{v}_{m{{{{{{{\rm{B}}}}}}}}}(k),\cdots )}^{{{{{{{{\rm{T}}}}}}}}}\), where m is the dimer line index from the edge. We consider \({v}_{m{{{{{{{\rm{A}}}}}}}}}(k)={(-1-a{e}^{ik}-a{e}^{-ik})}^{m-1}\) and vmB(k) = 0 as a zero energy partially flat band’s eigenvector. One can note that this choice of the eigenvector corresponds to a Q-CLS, which has nonzero amplitudes only in a finite region for each given m. An example of the Hamiltonian matrix of the semi-infinite system satisfying HSIv(k) = 0 is given by
where hk = 1 + aeik + ae−ik. v(k) is normalizable for π/2 < k < 3π/2 when a < 1 and \(\pi /2 < k < {\cos }^{-1}(-1/a)\) or \(2\pi -{\cos }^{-1}(-1/a) < k < 3\pi /2\) when a≥1. Since the boundaries of this momentum interval correspond to the band-crossing points, the corresponding bulk Hamiltonian \({H}_{{{{{{{{\rm{bulk}}}}}}}}}=(1+2a\cos {k}_{x}+\cos {k}_{y}){\sigma }_{x}+\sin {k}_{y}{\sigma }_{y}\), where σα is the Pauli matrix, leads to a topological semimetal with four Dirac nodes.
Discussion
By considering semi-infinite systems, we have shown that the partially flat band appears in a momentum range, where the corresponding Bloch summations of the Q-CLSs are normalizable. As a result, when we construct Wannier functions, the integration range of the Bloch wave functions in the momentum space is smaller than the entire Brillouin zone, leading to the algebraically decaying behavior. Therefore, we have demonstrated that the Wannier obstruction can happen even in a topologically trivial band.
While we have only considered semi-infinite systems, one might wonder, regarding realistic systems, whether the Wannier obstruction can be applied to finite systems or not. Here, the term finite system implies that the system’s size is finite along the directions with broken translational symmetry. Graphene nanoribbons with finite width are examples. In such finite systems, where one can construct regular finite-size Bloch Hamiltonians, the ghost flat band cannot exist, and each edge band should be smoothly connected to one of the bulk bands. Therefore, the conventional Wannierization with exponentially localized wave packets should be achieved in these systems. However, we show that the algebraic decaying behavior dominates in the Wannier function as the system size increases. This is because the edge modes are unaffected by the system size, while the bulk mode’s amplitude at each site diminishes as the size grows. As a result, the Wannier function decays exponentially only extremely far from its center, where the bulk wave function’s amplitude becomes comparable to that of the Wannier function. As an example, we consider a finite-size zigzag graphene nanoribbon. Its band structure is drawn in Fig. 3(c) for the ribbon width Q = 50, where the red and blue bands host nearly flat bands, corresponding to the edge modes, near the zone boundary. By applying a small perturbation, the red and blue bands are detached so that one can construct the Wannier function for them properly. Then, the red band’s Wannier function is plotted in Fig. 3(d) for various dimer lines, which exhibit the expected algebraic decay.
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Mielke, A. Ferromagnetism in the hubbard model and hund’s rule. Phys. Lett. A 174, 443 (1993).
Tasaki, H. From nagaoka’s ferromagnetism to flat-band ferromagnetism and beyond: an introduction to ferromagnetism in the hubbard model. Prog. Theor. Phys. 99, 489 (1998).
Hase, I., Yanagisawa, T., Aiura, Y. & Kawashima, K. Possibility of flat-band ferromagnetism in hole-doped pyrochlore oxides Sn2Nb2O7 and Sn2Ta2O7. Phys. Rev. Lett. 120, 196401 (2018).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605 (2019).
Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken chern insulators in twisted bilayer graphene. Nat. Phys. 17, 478 (2021).
Aoki, H. Theoretical possibilities for flat band superconductivity. J. Superconduct. Nov. Magn. 33, 2341 (2020).
Volovik, G. The fermi condensate near the saddle point and in the vortex core. JETP Lett. 59, 830 (1994).
Volovik, G. E. Graphite, graphene, and the flat band superconductivity. JETP Lett. 107, 516 (2018).
Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in moiré flat bands. Nat. Phys. 16, 725 (2020).
Yudin, D. et al. Fermi condensation near van hove singularities within the hubbard model on the triangular lattice. Phys. Rev. Lett. 112, 070403 (2014).
Liu, X. et al. Spectroscopy of a tunable moiré system with a correlated and topological flat band. Nat. Commun. 12, 1 (2021).
Peri, V., Song, Z.-D., Bernevig, B. A. & Huber, S. D. Fragile topology and flat-band superconductivity in the strong-coupling regime. Phys. Rev. Lett. 126, 027002 (2021).
Wu, C., Bergman, D., Balents, L. & Sarma, S. D. Flat bands and wigner crystallization in the honeycomb optical lattice. Phys. Rev. Lett. 99, 070401 (2007).
Chen, Y. et al. Ferromagnetism and wigner crystallization in kagome graphene and related structures. Phys. Rev. B 98, 035135 (2018).
Jaworowski, B. et al. Wigner crystallization in topological flat bands. N. J. Phys. 20, 063023 (2018).
Wang, F. & Ran, Y. Nearly flat band with chern number C= 2 on the dice lattice. Phys. Rev. B 84, 241103 (2011).
Tang, E., Mei, J.-W. & Wen, X.-G. High-temperature fractional quantum hall states. Phys. Rev. Lett. 106, 236802 (2011).
Sun, K., Gu, Z., Katsura, H. & Sarma, S. D. Nearly flatbands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Sheng, D., Gu, Z.-C., Sun, K. & Sheng, L. Fractional quantum hall effect in the absence of landau levels. Nat. Commun. 2, 1 (2011).
Regnault, N. & Bernevig, B. A. Fractional chern insulator. Phys. Rev. X 1, 021014 (2011).
Liu, Z., Bergholtz, E. J., Fan, H. & Läuchli, A. M. Fractional chern insulators in topological flat bands with higher chern number. Phys. Rev. Lett. 109, 186805 (2012).
Bergholtz, E. J. & Liu, Z. Topological flat band models and fractional chern insulators. Int. J. Mod. Phys. B 27, 1330017 (2013).
Rhim, J.-W., Kim, K. & Yang, B.-J. Quantum distance and anomalous landau levels of flat bands. Nature 584, 59 (2020).
Hwang, Y., Rhim, J.-W. & Yang, B.-J. Geometric characterization of anomalous landau levels of isolated flat bands. Nat. Commun. 12, 6433 (2021).
Hwang, Y., Jung, J., Rhim, J.-W. & Yang, B.-J. Wave-function geometry of band crossing points in two dimensions. Phys. Rev. B 103, L241102 (2021).
Hwang, Y., Rhim, J.-W. & Yang, B.-J. Flat bands with band crossings enforced by symmetry representation. Phys. Rev. B 104, L081104 (2021).
Peotta, S. & Törmä, P. Superfluidity in topologically nontrivial flat bands. Nat. Commun. 6, 8944 (2015).
Mera, B. & Mitscherling, J. Nontrivial quantum geometry of degenerate flat bands. Phys. Rev. B 106, 165133 (2022).
Oh, C.-g., Cho, D., Park, S. Y. & Rhim, J.-W. Bulk-interface correspondence from quantum distance in flat band systems. Commun. Phys. 5, 320 (2022).
Yu, J. et al. Non-trivial quantum geometry and the strength of electron–phonon coupling. Nat. Phys. (2024).
Tian, H. et al. Evidence for dirac flat band superconductivity enabled by quantum geometry. Nature 614, 440 (2023).
Jung, J., Lim, H. & Yang, B.-J. Quantum geometry and landau levels of quadratic band crossing points. Phys. Rev. B 109, 035134 (2024).
Guzmán-Silva, D. et al. Experimental observation of bulk and edge transport in photonic lieb lattices. N. J. Phys. 16, 063061 (2014).
Vicencio, R. A. et al. Observation of localized states in lieb photonic lattices. Phys. Rev. Lett. 114, 245503 (2015).
Mukherjee, S. et al. Observation of a localized flat-band state in a photonic lieb lattice. Phys. Rev. Lett. 114, 245504 (2015).
Ma, J. et al. Direct observation of flatband loop states arising from nontrivial real-space topology. Phys. Rev. Lett. 124, 183901 (2020).
Milićević, M. et al. Type-iii and tilted dirac cones emerging from flat bands in photonic orbital graphene. Phys. Rev. X 9, 031010 (2019).
Taie, S. et al. Coherent driving and freezing of bosonic matter wave in an optical lieb lattice. Sci. Adv. 1, e1500854 (2015).
Drost, R., Ojanen, T., Harju, A. & Liljeroth, P. Topological states in engineered atomic lattices. Nat. Phys. 13, 668 (2017).
Jin, L. & Song, Z. Bulk-boundary correspondence in a non-hermitian system in one dimension with chiral inversion symmetry. Phys. Rev. B 99, 081103 (2019).
Kuno, Y. Extended flat band, entanglement, and topological properties in a Creutz ladder. Phys. Rev. B 101, 184112 (2020).
Zhang, S. M., Xu, H. S. & Jin, L. Tunable Aharonov-Bohm cages through anti-\({{{{{{{\mathcal{PT}}}}}}}}\)-symmetric imaginary couplings. Phys. Rev. A 108, 023518 (2023).
Mukherjee, S. & Thomson, R. R. Observation of localized flat-band modes in a quasi-one-dimensional photonic rhombic lattice. Opt. Lett. 40, 5443 (2015).
Zhang, S. M. & Jin, L. Localization in non-Hermitian asymmetric rhombic lattice. Phys. Rev. Res. 2, 033127 (2020).
Kang, M. et al. Topological flat bands in frustrated kagome lattice cosn. Nat. Commun. 11, 4004 (2020).
Liu, Z. et al. Orbital-selective dirac fermions and extremely flat bands in frustrated kagome-lattice metal cosn. Nat. Commun. 11, 4002 (2020).
Yin, J.-X. et al. Negative flat band magnetism in a spin–orbit-coupled correlated kagome magnet. Nat. Phys. 15, 443 (2019).
Kang, M. et al. Dirac fermions and flat bands in the ideal kagome metal fesn. Nat. Mater. 19, 163 (2020).
Lin, Z. et al. Flatbands and emergent ferromagnetic ordering in Fe3Sn2 kagome lattices. Phys. Rev. Lett. 121, 096401 (2018).
Di Sante, D. et al. Flat band separation and robust spin berry curvature in bilayer kagome metals. Nat. Phys. 19, 1135–1142 (2023).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43 (2018).
Rhim, J.-W. & Yang, B.-J. Singular flat bands. Adv. Phys.: X 6, 1901606 (2021).
Rhim, J.-W. & Yang, B.-J. Classification of flat bands according to the band-crossing singularity of bloch wave functions. Phys. Rev. B 99, 045107 (2019).
Leykam, D., Andreanov, A. & Flach, S. Artificial flat band systems: from lattice models to experiments. Adv. Phys.: X 3, 1473052 (2018).
Sathe, P., Harper, F. & Roy, R. Compactly supported wannier functions and strictly local projectors. J. Phys. A: Math. Theor. 54, 335302 (2021).
Kim, H., Oh, C.-g. & Rhim, J.-W. General construction scheme for geometrically nontrivial flat band models. Commun. Phys. 6, 305 (2023).
Fujita, M., Wakabayashi, K., Nakada, K. & Kusakabe, K. Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920 (1996).
Rhim, J.-W. & Moon, K. Edge states of zigzag bilayer graphite nanoribbons. J. Phys.: Condens. Matter 20, 365202 (2008).
Jaskólski, W., Ayuela, A., Pelc, M., Santos, H. & Chico, L. Edge states and flat bands in graphene nanoribbons with arbitrary geometries. Phys. Rev. B 83, 235424 (2011).
Burkov, A., Hook, M. & Balents, L. Topological nodal semimetals. Phys. Rev. B 84, 235126 (2011).
Deng, W. et al. Nodal rings and drumhead surface states in phononic crystals. Nat. Commun. 10, 1769 (2019).
Kim, Y., Wieder, B. J., Kane, C. & Rappe, A. M. Dirac line nodes in inversion-symmetric crystals. Phys. Rev. Lett. 115, 036806 (2015).
Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M. & Soluyanov, A. A. Nodal-chain metals. Nature 538, 75 (2016).
Son, Y.-W., Cohen, M. L. & Louie, S. G. Half-metallic graphene nanoribbons. Nature 444, 347 (2006).
Heikkilä, T. T., Kopnin, N. B. & Volovik, G. E. Flat bands in topological media. JETP Lett. 94, 233 (2011).
Bergman, D. L., Wu, C. & Balents, L. Band touching from real-space topology in frustrated hopping models. Phys. Rev. B 78, 125104 (2008).
Kohn, W. Analytic properties of bloch waves and wannier functions. Phys. Rev. 115, 809 (1959).
Brouder, C., Panati, G., Calandra, M., Mourougane, C. & Marzari, N. Exponential localization of wannier functions in insulators. Phys. Rev. Lett. 98, 046402 (2007).
Po, H. C., Watanabe, H. & Vishwanath, A. Fragile topology and wannier obstructions. Phys. Rev. Lett. 121, 126402 (2018).
Des Cloizeaux, J. Analytical properties of n-dimensional energy bands and wannier functions. Phys. Rev. 135, A698 (1964).
Acknowledgements
We are funded by the National Research Foundation of Korea(NRF) Grant funded by the Korean government (MSIT) (Grant Nos. 2021R1A2C1010572, 2022M3H3A106307411, and 2021R1A5A1032996) and the Ministry of Education (Grant no. RS-2023-00285390).
Author information
Authors and Affiliations
Contributions
J. W. R. conceived the initial idea and supervised the project. J. H. P. performed the theoretical analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Alexei Andreanov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Park, JH., Rhim, JW. Quasi-localization and Wannier obstruction in partially flat bands. Commun Phys 7, 179 (2024). https://doi.org/10.1038/s42005-024-01679-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-024-01679-6
- Springer Nature Limited
We’re sorry, something doesn't seem to be working properly.
Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.