Introduction

Epidemic spreading on networks has been an active research area in modern network science. Earlier, the interplay between epidemics and network structures was a focus1,2,3,4. Human behaviors are then recognized as a major factor affecting the epidemic trajectories on local and global scales5,6,7,8. Among the diverse behaviors, human mobility is key to disease spreading9. From the daily short-term commuters in large metropolitan areas to long-range travel via flights, trains, and buses, human mobility10,11,12 plays a key role in shaping the spatiotemporal patterns of global epidemics13,14,15. Indeed, the modern transportation infrastructures of varying scales have made human beings much more connected16,17. Infectious diseases thus propagate unprecedentedly faster and more widely and can evolve into a global pandemic18. For example, the rapid spread of SARS-CoV-2 all over the world leading to the COVID-19 pandemic can largely be attributed to travel19.

In terms of mathematical modeling, a number of frameworks are presently available for studying the impacts of human mobility on epidemic spreading, e.g., metapopulation network dynamics at the population level and multilayer networks at the individual level. In a metapopulation network, nodes represent subpopulations such as communities, cities, or countries, whereas edges between nodes describe human mobility between two subpopulations and the edge weights characterize the scale or strength of human mobility20. Epidemic spreading among the subpopulations can be modeled as reaction-diffusion and reaction-commuting processes21,22,23,24,25, where the reaction process describes the infection dynamics within the subpopulations, diffusion and commuting represent the mobility of population among the nodes. In this type of model, infected populations move and carry pathogens between the nodes, leading to an outbreak of infectious disease at the scale of the whole system. An example is the modeling of the COVID-19 pandemic, where models based on the metapopulation networks were developed to fit and predict the spreading trajectories and to evaluate the effects of different non-pharmaceutical interventions15,26. At the individual level, multilayer networks have been used to study the impacts of mobility on epidemic spreading27,28. In a multilayer network, the layers represent different types of connections among nodes, such as social contacts of individuals in different cities or on different social platforms, transportation by different modes, and different types of financial business among banks17,29, where the dynamical interplay and couplings between the layers can alter the global epidemic threshold and the spreading dynamics3,30,31.

While human mobility has been recognized as an important factor in modeling epidemic spreading in society, the roles of infection and recovery during travel that make the process fundamentally non-Markovian have not been addressed. It was recognized that infectious diseases can be transmitted and spread during air or land travel32,33,34, which not only changes the spatial distribution of the hosts but also accelerates the spreading process and increases the total size of infection35. Based on the human mobility data, models that incorporate the infection during travel can predict the evolution and peaks of the pandemic well36,37,38. In these works, the travel process was assumed to be “instantaneous” without any memory effect. In particular, travel between different regions was modeled by a rate parameter—the probability that individuals start from one region and arrive in another, and the future occurrence can be predicted based solely on the present state of the system. Mathematically, such a process is said to be Markovian. However, many human activities, from communications to mobility, are not memoryless, which should be modeled as non-Markovian processes39,40,41. In network epidemics, a non-Markovian process with memories can significantly alter the spreading dynamics42,43,44,45,46. When individuals conduct a long-distance journey, they may travel by flights, trains, buses or boats. During travel, infections can occur when travelers take the same transportation means with similar departure and arrival times. It takes a certain amount of time for the travelers to contact and infect each other during the travel process. Meanwhile, when a pandemic breaks out, such as COVID-19, travelers may be quarantined for a period of time when arriving in a new city, a new district, or a country. These observations suggest the necessity to treat travel with infections as a non-Markovian dynamical process. To our knowledge, incorporating non-Markovian travel dynamics into the epidemic spreading model represents a knowledge gap in the field. The purpose of our work is to fill this gap.

This paper presents a comprehensive treatment of epidemic spreading dynamics incorporating non-Markovian travel in multilayer networks. For simplicity, we consider a double-layer system, where infection and recovery occur both within the layers and during the travel between the layers. We introduce a quantity to characterize the non-Markovian travel process: the travel age that records the time a traveler is in transit. In particular, a traveler is exposed to contact with other travelers but only of the same travel direction and travel age. When the travel age is equal to the time required to arrive at the destination, the trip is regarded as completed. Based on the quenched mean-field theory (QMF), we derive the non-Markovian dynamical equations to describe the spreading dynamics in the double-layer system. We find that travel infections do not necessarily promote the spreading in the whole system in the sense of a reduced epidemic threshold but, counter-intuitively, can even increase it under different travel strengths (see below for a definition). An optimal travel strength can emerge at which the epidemic threshold reaches a maximum. Strikingly, with an increase in the travel time between the layers, the epidemic threshold first decreases and then enters a two-threshold region where, due to the recovery of the infected individuals during the travel, the outbreak size of the epidemic with a small infection rate is larger than that of an epidemic with a large infection rate. When the travel time is sufficiently large (e.g., with quarantine), the epidemic threshold finally reaches a high value. The time at the onset of the high threshold value can be taken as the minimally required time for quarantine. It is worth emphasizing that, in the Markovian travel model, only the outbreak peak is reduced as the travel time increases, while the outbreak time and the epidemic duration rarely change. In contrast, non-Markovian travel will result in a higher epidemic threshold, a delayed outbreak time and a longer epidemic duration. Our results thus justify that, for our simple model with non-Markovian travel, by increasing the travel time or the quarantine time, one can flatten the infection curve to mitigate the epidemic.

Results

Epidemic spreading model with travel infections

We articulate an epidemic spreading model supported on a double-layer networked system with non-Markovian travel infections. The system hosts two kinds of individuals: permanent residents in each layer and travelers; permanent residents stay within the layer, and travelers can either stay within a layer or travel between the layers along the interlayer edges. Permanent residents have connections only in their local layer, while travelers have connections in both layers. For travelers, the network connections within a layer are activated only when they are in that layer. Travelers can make contact with others and spread the disease within the layers and during the travel.

Figure 1 presents a schematic diagram of our non-Markovian model, where the networks in layers A and B have the same size N. Each traveler generates an interlayer link. Let mN be the number of travelers in the system, where 0 < m < 1. The total number of individuals in the network layers is then Ntot = (2 − m)N. At each time step, a number of travelers from layer A (B) initiate their trip at the rate qA (qB) and then travel along the interlayer link A → B (B → A). For simplicity, we set qA = qB = q. Travelers who travel in the same direction and have the same travel age can contact with each other at the probability α. The time travelers have spent on the trip is their travel age l. When the travel age l equals the travel time tT—the total time required to arrive at the destination layer since starting a trip (including quarantine time, if any), the trip is completed. For simplicity, we use a fixed value of α for the travel time and quarantine period. However, in reality, the contact rates should be different for travel and quarantine periods, where the contact rate in quarantine should be relatively low in a controlled environment. As the travelers take a certain time to arrive at the destination layer, the memory effect is naturally integrated into the model, making the process non-Markovian. (In contrast, for a Markovian travel process, the travelers would jump to the destination layer instantaneously44 at the rate 1/tT. In this case, since there is no travel age, all travelers on the trip contact with each other at the rate α/tT.)

Fig. 1: Schematic illustration of the proposed epidemic spreading model with non-Markovian travel infections.
figure 1

There are four types of nodes in the network: the layer permanent residents (green solid circles), travelers in layer A or on the A → B interlayer links (yellow solid circles), travelers in layer B and on the B → A interlayer links (blue solid circles), and the nodes left by the travelers (open circles). A traveler has a pair of nodal positions, one in each layer, which are connected by an interlayer link. When travelers stay in a layer, they can contact with their neighbors within the layer (solid lines within each layer). Otherwise, their connections are deactivated (dashed lines in both layers). Travelers departing from the same layer at the same time form a fully connected subnetwork during the trip with the contact rate α. Travelers will arrive at the destination layer when their travel age l equals the travel time tT.

Full size image

In the real world, the number of travelers between two cities is generally stable over a long period of time, while an epidemic typically occurs in an abrupt manner. It is thus reasonable to assume in our model that the distribution of travelers between the two layers has reached a steady state before the epidemic begins. We use the standard SIR model to describe the spreading dynamics within each layer and on the trip, where a node can be in one of the three states: susceptible (S), infected (I) and recovered (R). At each time step, an I-node contacts and transmits disease to its susceptible neighbors at the rate β (the infection rate) and then transitions to the R-state at the rate μ (the recovery rate). Nodes in the R-state will not be infected anymore and remain in this state. The epidemic process terminates when there are no longer any I nodes in the system. An epidemic outbreak occurs when the infection rate β is greater than a critical value47, denoted as the epidemic threshold βc, and the outbreak size is the fraction of R nodes in the steady state. The epidemic threshold can be determined empirically by calculating the outbreak size31,48: the threshold is the minimal value of the infection rate β at which the outbreak size exceeds a small but not insignificant value (0.01 in our work). For SIR spreading dynamics, the approach of discrete-time modeling has been extensively used4. In general, there are two types of state updating rules for individual nodes: synchronous and asynchronous updating. In synchronous updating, infection occurs first, followed by recovery3,49,50. In this case, the order of events is definite: in one time step with interval Δt, a susceptible node i becomes infected with the probability \(1-{(1-{\beta} {\Delta} {t})}^{n_{i}}\) is the number of this node’s infected neighbors. Then, all infected nodes recover with the probability μΔt. When μΔt or Δt is sufficiently small, the discrete-time dynamics associated with synchronous updating approach those with the asynchronous updating rule51,52. We use the synchronous updating method to simulate the spreading process, which requires careful parameter selection to ensure simulation accuracy53.

Impacts of travel strength on epidemic threshold

We first study the impacts of travel strength on the spreading dynamics, where the travel strength is characterized by the fraction m and the travel rate q of the travelers. Figure 2a–c shows the change in the epidemic threshold as a function of the traveler fraction m for different travel time tT, denoted as \({\beta }_{c}^{T}\). For tT = 1, an optimal travel fraction arises (m ≈ 0.15) at which the epidemic threshold is the highest, where \({\beta }_{c}^{T}\) first increases and then decreases at tT = 1, as shown in Fig. 2a. This behavior can be understood by noting that the departure of the travelers reduces the mean active degree within each layer, thereby leading to an increase in the epidemic threshold, while contacts during the trip promote the infections among the travelers so as to reduce the threshold. As a comparison, we calculate the epidemic threshold \({\beta }_{c}^{H}\) of a two-layer system with travelers hopping between layers but without travel infections31, as well as the epidemic threshold \({\beta }_{c}^{S}\) for a single-layer network. Without travel infections, the threshold \({\beta }_{c}^{H}\) increases monotonically with m and is larger than \({\beta }_{c}^{T}\) and \({\beta }_{c}^{S}\), as the result of reduced contacts and infections within the layers due to the travel. When travel infections are taken into account, the epidemic threshold \({\beta }_{c}^{T}\) first increases and then decreases to values smaller than that of the single layer. For tT = 4, βc is nearly constant for m < 0.1 and then decreases rapidly for m > 0.1, as shown in Fig. 2b. For tT = 16, the epidemic threshold \({\beta }_{c}^{T}\) reaches a local maximum at m ≈ 0.5, as shown in Fig. 2c. These results indicate that travel infections can have a significant effect on the dynamics with a complicated dependence of the epidemic threshold on the travel time.

Fig. 2: Dependence of epidemic threshold on the travel strength.
figure 2

a–c Epidemic threshold as a function of traveler fraction m for tT = 1, 4, and 16, respectively, for q = 0.1. In (a), \({\beta }_{c}^{T}\) (blue squares), \({\beta }_{c}^{H}\) (orange circles), and \({\beta }_{c}^{S}\) (the gray line) are the epidemic thresholds from the model with travel infections, the interlayer hopping model without travel infections, and a single-layer network, respectively. The increase of \({\beta }_{c}^{H}\) with m is due to the departure of the travelers from each layer, which is larger than \({\beta }_{c}^{S}\). The threshold \({\beta }_{c}^{T}\) first increases and then decreases with m, where the former is due to the departure-induced reduction of infection in each layer, and the latter is caused by travel infections. For a long travel time, \({\beta }_{c}^{T}\) exhibits a peak (c). d–f Epidemic threshold versus the travel rate q for tT = 1, 4 and 16, respectively, for m = 0.2. Other parameters are α = 1 and μ = 0.5. Each layer is an ER random network with size N = 1 × 104 and average degree 〈k〉 = 10. Each data point is averaged over 103 network realizations.

Full size image

Figure 2d–f shows the epidemic threshold versus the travel rate q for three different values of the travel time tT: tT = 1, 4, and 16, respectively. For tT = 1 [Fig. 2d] and 4 [Fig. 2e], \({\beta }_{c}^{T}\) decreases with q initially but tends to a constant (approximately) for q ≳ 0.5. The initial decrease in the epidemic threshold is the result of increasing contact among travelers as more individuals begin to travel, thereby promoting the disease spreading. However, when the travel rate q becomes large, the travelers do not stay in one layer for a relatively long time, so the spreading dynamics in each layer are suppressed. For a sufficiently long travel time, e.g., tT = 16 [Fig. 2f], the threshold is hardly impacted by the travel rate q.

The behaviors in Fig. 2a–f entail that the impacts of different m and q values on the epidemic threshold can be understood in terms of the contact activities. Especially for a fixed q value, an optimal m value can emerge at which the epidemic threshold is the highest (see Supplementary Note 1 for details). We have also studied double-layer network configurations with the heterogeneous ER-SF (scale-free) and SF-SF combinations and obtained similar results (Supplementary Note 2).

Impacts of travel time on epidemic spreading dynamics

Figure 2a–f illustrates that the dependence of the epidemic threshold on the traveler fraction m and travel rate q can vary with the travel time tT resulting from, e.g., different transportation modes (airplane, train, or boat). Since the hallmark of non-Markovian travel is a finite travel time in our model, it is useful to investigate the effects of the travel time tT on the spreading dynamics. Figure 3a, b shows how the steady-state outbreak size R(∞) is affected by tT and the infection rate β. In particular, Fig. 3a reveals that, for β = 0.1, the outbreak size decreases with tT. However, for β = 0.02 or β = 0.04, R(∞) first increases and then decreases with tT. Figure 3b shows that the dependence of R(∞) on β also varies for different values of tT. For example, for tT = 8, R(∞) first increases and then decreases toward an approximately near zero value but finally increases rapidly with β. The results in Fig. 3a, b suggest rather complex impacts of the travel time on the spreading dynamics.

Fig. 3: Dependence of epidemic outbreak size on travel time and infection rate.
figure 3

Outbreak size versus a the travel time tT for different values of the infection rate and b the infection rate β for different travel times. c Theoretical prediction and d the corresponding numerical results of the final infection size R(∞) shown as color-coded values in the parameter plane (tT, β). For tT > 1, a two-threshold phenomenon arises, where the black dashed line in each panel represents the epidemic threshold when there is only infection but no recovery during the travel, and the black dash-dotted line denotes the epidemic threshold when infection occurs only once—at the first time step during the travel, while there is only recovery for the remaining travel time, a situation that arises when a mandatory quarantine is imposed at the travel destination. The emergence of the second (higher) threshold can thus be interpreted as the result of quarantine. Other parameters are m = 0.4, q = 0.1, α = 1 and μ = 0.5. Each layer is an ER network of size N = 1 × 104 and average degree 〈k〉 = 10. Each data point is the result of averaging over 103 statistical realizations.

Full size image

To understand the impact of non-Markovian travel on the spreading dynamics, we have developed a theoretical framework based on the quenched mean-field (QMF) approximation (see “Methods”). Figure 3c, d presents the theoretically predicted and numerically calculated phase diagram of the steady-state infection size R(∞), respectively, in the parameter plane (tT, β). In Fig. 3c, we divide the diagram into three regions according to the travel time tT: \({t}_{T}\in \left[1,7\right)\), \({t}_{T}\in \left[7,12\right]\) and \({t}_{T}\in \left(12,20\right]\). In the first region, R(∞) increases with the infection rate β. In the second region, R(∞) first increases with β, and the epidemic breaks out at the first threshold. The infection size then decreases with β to a small value under 0.01. The epidemic breaks out again as β increases through a second threshold, and R(∞) continues to increase with β afterward. This is a two-threshold phenomenon due to the interplay between the infection and recovery of the travelers during the travel process where, when β varies between the two thresholds, the infection size with a low infection rate is larger than that associated with a high infection rate. In the third region, where the travel time is relatively long, the infection size first increases slowly with β and remains small for a large range of β. When β is sufficiently large, an outbreak occurs, and R(∞) increases with β. In spite of the slightly larger theoretical value of R(∞) due to the “echo chamber” effect in solving the dynamical evolution equations54, there is a general agreement between the theoretical and numerical results.

The two-threshold phenomenon illustrated in Fig. 3 is the result of the recovery involved in the non-Markovian travel dynamic, which can either promote or suppress epidemic in the whole double-layer system. In particular, the black dashed line in Fig. 3c, d represents the epidemic threshold when there is only infection but no recovery (recovery rate μ = 0) during the travel, which agrees with the low epidemic threshold predicted by the QMF theory. The low threshold decreases with tT, indicating that the travel infections promote epidemic spreading in the system. The black dash-dotted line represents the epidemic threshold when there are contacts and infections only at the first time step in the travel process, while in the remaining tT − 1 time steps, there is only recovery. This corresponds to the real-world situation where travelers are quarantined for a period of time when they arrive at their destinations. In this case, increasing the travel time (quarantine time) can result in an increase in the epidemic threshold that agrees with the high epidemic threshold predicted by our theory, indicating that travel recovery suppresses the epidemic spreading in the whole system.

To understand how the infection within the layers and during travel affect the outbreak size of the entire system, we calculate and analyze the numbers of two types of individuals: the cumulative numbers of individuals infected within the layers and during the travel, denoted as nLL and nEE, respectively. We also calculate the number nEL of the infected individuals switching from the travel process to the layers and the cumulative number nLE of the infected individuals transitioning from layers to the interlayer edges. (Details of how nLL, nEE, nEL and nLE are calculated are given in Supplementary Note 3). We also find that the critical (small) tT value at which the two-threshold phenomenon disappears is mainly determined by the recovery rate μ, where a large value of μ leads to a small critical tT (Supplementary Note 4). The reason is that if the infected individuals are able to recover in a short time, they will have sufficient time to recover during the trip, even when the travel time tT is small. Furthermore, when the contact ability α during travel reduces to values less than one, insofar as the contacts between travelers are more frequent than those within each layer, the two-threshold phenomenon persists (see Supplementary Note 4 for details), where the low threshold increases as α decreases. The phenomenon ceases to exist but only when α is reduced to a quite small value, e.g., 0.1, where the average degrees of the contact network during travel and of the layer are equal. It is worth noting that such small values of α are not physically meaningful, as the contacts during travel are typically much more frequent than those within a layer in our model, which is the case for respiratory disease and in large-capacity public vehicles such as trains and airplanes. In addition, we preliminarily explore the impact of the restricted number of contacts during travel on the two-threshold phenomenon, as is detailed in Supplementary Note 5. It is found that the two-threshold phenomenon may be susceptible to the risk of interlayer infection and becomes more obvious with increasing the network size. However, it is also necessary to explore the impact of the restricted number of contacts during travel on the epidemic dynamics in multilayer networks, especially to find out whether all the results are finite size-dependent and do hold in the thermodynamic limit.

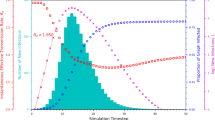
Figure 4 presents the time evolution of the prevalence ρ(t) for different values of the infection rate β. For low infection rates (β = 0.02 in Fig. 4a and β = 0.04 in Fig. 4b), multiple outbreak peaks arise. In this case, the epidemic does not break out in the layers [Supplementary Fig. 4c in Supplementary Information]. On the contrary, travelers with the same travel age and direction are fully connected during the trip, leading to an outbreak and an increase in ρ(t). When some travelers have arrived at the destination layer, ρ(t) decreases because the infection rate is too small to induce an outbreak within the layer. However, when the travelers start to travel again, ρ(t) can increase. The non-Markovian travel process with the memory effect well captures the feature of the multiple peaks when travel infections dominate the epidemic dynamics in the system. For β = 0.04, since the infection and recovery are faster than those for β = 0.02, the number of infections arriving at the destination layer decreases. This results in a rapid decrease in the subsequent infection peaks. For β = 0.1 [Fig. 4c], infections can break out both within the layers and during the travel, so ρ first increases and then decreases. For t ≈ 4, a small peak in ρ arises due to the fact that, during a few initial time steps, infections within the layers have not broken out, and they mainly come from the travel process.

Fig. 4: Time evolution of prevalence.
figure 4

Shown is the evolution of ρ(t) for a β = 0.02, b β = 0.04 and c β = 0.1. The travel time is tT = 8. The distinct feature is the occurrence of multiple peaks in ρ(t) during its time evolution—see text for details. Other parameter values are m = 0.4, q = 0.1, α = 1 and μ = 0.5.

Full size image

Comparison with Markovian travel process

To emphasize the fundamental importance of non-Markovian travel in epidemic spreading, we carry out a comparison study of the spreading dynamics with Markovian and non-Markovian travel. Figure 5 shows that, due to the memory effects in travel infections, non-Markovian travel leads to a higher epidemic threshold than that with Markovian travel. In particular, in a non-Markovian travel process, only travelers with the same travel age and direction can form a connected network to spread the disease, which lasts for a time length of tT. However, for a Markovian travel process, infected individuals can contact with all other travelers and return to the layer at the rate 1/tT, while the infected individuals remaining in the travel state can continue to infect other travelers, which in turn promote the infections in the layers. Note that, for both types of travel, the epidemic threshold decreases with m [Fig. 5a] and q [Fig. 5b], indicating that travel, in general, promotes epidemic spreading. When q is large, βc with non-Markovian travel increases. This is because travelers cannot stay in one layer for a relatively long time, which in turn suppresses the epidemic spreading in each layer. The change of the epidemic threshold with m and q at different tT is analyzed in Supplementary Note 6.

Fig. 5: Comparison between epidemic dynamics with non-Markovian and Markovian travel.
figure 5

Shown is the epidemic threshold βc versus the traveler fraction m, the travel rate q, and the travel time tT for non-Markovian travel and Markovian travel: a βc versus m for q = 0.1 and tT = 8, b βc versus q for m = 0.2 and tT = 8, and c βc versus tT for q = 0.1 and m = 0.4. In both cases, βc decreases continuously with m and q. However, as the travel time increases, a two-threshold phenomenon occurs for the non-Markovian travel model: the threshold remains low until a critical time is reached, at which the threshold abruptly increases to a much larger value. This means that the epidemic is greatly suppressed if the travel time is longer than the critical time, providing a quantitative criterion to determine the necessary quarantine time to effectively suppress the epidemic because, after the quarantine, the infection rate needs to be much higher (possibly biologically infeasible) to lead to an outbreak. In stark contrast, the Markovian travel spreading model, by design, is unable to take quarantine into account, rendering it inapplicable to modeling real-world epidemics that involve travel. The symbols are numerical results, and the curves are the corresponding theoretical predictions from the dynamical equations (solid) and the Jacobian matrix method (dashed). Other parameters are set as α = 1 and μ = 0.5.

Full size image

A remarkable phenomenon occurs for epidemics with non-Markovian travel, where the epidemic threshold remains low and nearly constant until the travel time exceeds a large critical value, at which an abrupt increase in the threshold occurs. A representative result is shown in Fig. 5c, where the epidemic threshold βc versus the travel time tT for both types of travel dynamics is displayed. For the non-Markovian process, βc first decreases with tT. When tT varies in the range [7, 12], a two-threshold phenomenon occurs where, for a certain tT, a small-scale epidemic breaks out at a low epidemic threshold. As the infection rate increases, the infection size decreases to a small value of about 0.01. Only when the infection rate increases through the second (higher) epidemic threshold will another outbreak become possible. For sufficiently long travel, e.g., tT > 12, the epidemic threshold increases with tT. A long travel time, in general, is the result of government-imposed quarantine, and Fig. 5c provides a quantitative criterion to determine the minimal quarantine time: quarantine must be sufficiently long to ensure that a high epidemic threshold is achieved! In the particular setting of Fig. 5c, the minimal quarantine time should be about tT ~ 12. It should be noted that, in the Markovian travel model, travel between the network layers is an instantaneous process that occurs at the rate 1/tT, so tT here is a mere model parameter: it is not indicative of any kind of actual travel time. In this case, as shown by the orange circles and curve in Fig. 5c, βc decreases rapidly for small tT as travel promotes spreading and then starts to increase slowly because of the continuous reduction in the switching rate from the trip to the layers, implying that quarantine would have no effect in suppressing the epidemics and rendering invalid any model with Markovian travel.

We have also examined the time evolution of the prevalence ρ for different values of the infection rate β for the non-Markovian and Markovian travel models, as shown in Fig. 6a–d. It can be seen that the non-Markovian travel model has a lower infection peak, a delayed outbreak time, and a longer infection duration than that of the Markovian travel model. The difference can be quite significant, especially for small values of β, as shown in Fig. 6a because, in this case, the infections incurred during the travel are the main contributing factor to the epidemic in the whole system. The multiple outbreaks exemplified in Fig. 6a are the result of the memory effects associated with non-Markovian travel. As β increases, the epidemic can break out both within the layers and during travel, so the differences from the travel process become less significant, as shown in Fig. 6b, c, and exemplified in Fig. 6d. These results indicate that, compared with the more realistic non-Markovian travel model, the Markovian travel model overestimates the epidemic threshold and the infection peak but underestimates the spreading time. Furthermore, we find that increasing the travel time tT leads to a reduced outbreak peak, a delayed outbreak time and a longer epidemic duration in the non-Markovian travel model, which are not found in the Markovian travel model, as shown in Supplementary information Note 6 (Supplementary Fig. 9). The non-Markovian travel model provides evidence for the effectiveness of travel time in moderating the development of epidemic.

Fig. 6: Comparison of time evolution of prevalence between non-Markovian travel (NMT) and Markovian travel (MT) epidemic models.
figure 6

a–d Time evolution ρ(t) and e–h time evolution of the layer prevalence ρL(t) (dashed curves) and the travel prevalence ρE(t) (solid curves) for β = 0.05, 0.1, 0.2, and 0.4, respectively. Other parameters are set as m = 0.4, q = 0.1, tT = 4, α = 1 and μ = 0.5.

Full size image

Additional insights into the difference between the non-Markovian travel and Markovian travel epidemic dynamics can be gained by distinguishing the evolution of the prevalence from the layers and the travel process, denoted as ρL(t) and ρE(t), respectively. Figure 6e–h shows that, as the infection rate β increases from 0.05 to 0.4, the fraction of the infections from travel decreases, indicating that the effect of travel infections is more significant when the infection rate is small. Since, for non-Markovian travel, the travelers return to layers when their travel age is tT, multiple infection peaks in ρE can arise, as shown in Fig. 6e, where the highest peak is lower and occurs later than that from the Markovian travel model. For the Markovian travel model, infected individuals return to the layer at the rate 1/tT, and the remaining infected individuals in the travel process can continue to infect other travelers, leading to an earlier onset of the epidemic outbreak than that in the non-Markovian travel model. As β increases and the effects of travel infections decrease [Fig. 6f–h], the differences between the two travel models become less significant.

Discussion

In large-scale epidemic spreading such as the COVID-19 pandemic, travel is an indispensable and perhaps one of the most significant contributing factors. To properly incorporate travel into epidemics is essential to rendering the model predictions relevant to the real world. Previous models taking travel into account used an overly simplistic approach: travel has been treated as a Markovian process without any memory effect, i.e., travel is assumed to occur instantaneously at a certain rate. Because of this idealization, issues pertinent to making travel policies and guidelines during the pandemic cannot be addressed by models with Markovian travel. To provide informed policies backed up by quantitative science, the non-Markovian nature of the travel process must be taken into account. For example, when a large epidemic occurs, an important issue is for the authorities to determine the minimal quarantine time based on quantitative model predictions. Our present work represents an initial step in this direction by developing a framework to incorporate realistic, non-Markovian travel into epidemic modeling. While there are many mechanisms by which a spreading process can become non-Markovian, e.g., through a non-exponential distribution of infectiousness, for spreading dynamics incorporating travel, an intuitive and reasonable way is to set a non-zero, constant travel time.

Our model is a two-layer network system, where travel between the layers is non-Markovian, a process that requires a finite amount of time to complete. In spite of the complexity introduced by the non-Markovian travel, the model is analytically tractable. Through mathematical analyses and extensive numerical simulations, our model captures a number of phenomena. First, due to the non-Markovian nature, travel infections do not necessarily promote the epidemic spreading in the system. In fact, there is an optimal travel strength at which the epidemic threshold reaches a maximum. Second, but more importantly, as the travel time increases, the epidemic threshold can exhibit a remarkable two-threshold behavior. In particular, when the travel time is below a critical value, the epidemic threshold is low, making a large-scale outbreak possible. The finding is an abrupt and significant increase in the threshold as the travel time exceeds the critical value. This means that to suppress the epidemic, the travel time should be longer than some critical value. Third, we have analyzed the effects of contact ability in the travel process and found that, for infectious diseases with a high infection rate, reducing the contact in travel is generally ineffective in suppressing the disease (Supplementary Note 7). Compared with epidemic models with the simplistic Markovian travel process, our non-Markovian model induces a higher epidemic threshold and a delayed outbreak time at the price of a longer infection period and also generates the real-world phenomenon of multiple infection peaks.

Our non-Markovian travel-based framework provides a complex network approach to addressing the role of human behaviors in spreading dynamics. The framework is demonstrated to be successful in capturing real-world phenomena, such as the effectiveness of quarantine strategy and the occurrence of multiple outbreak peaks as widely witnessed since the beginning of the COVID-19 pandemic. The emergence of a two-threshold region in the epidemic threshold with respect to the traveling time may provide a quantitative estimation of the necessary quarantine time for travelers. The delayed outbreak time and a longer epidemic duration in our non-Markovian model imply the effects of travel time and quarantine time on flattening the infection curve, where a moderate epidemic has the advantage of causing less stress on the healthcare system. The results of our comparative analysis have essentially denied the use of Markovian travel-based epidemic models to capture the role of real-world travel in epidemics. All these indicate the absolute necessity to use a non-Markovian process to incorporate human behaviors into epidemic modeling.

In our model, there are some simplifying assumptions, including a fixed travel time (as opposed to a distribution) to characterize non-Markovian travel, the assumption of a fully connected network during trips, the adoption of Markovian epidemic spreading dynamics, and the absence of additional non-pharmacological interventions. A potential topic for future investigation is considering more realistic travel processes with larger-scale populations (such as metapopulation networks and agent-based models), where travel times exhibit a distribution and individual heterogeneity is taken into account. The traveler on trip should be further divided into different connected groups to represent that travelers will be within different vehicles of fixed capacity. Another open issue is to integrate travel infections into travel-based non-pharmaceutical interventions aimed at effective epidemic control. Introducing non-Markovian travel into more realistic models holds promise for yielding meaningful outcomes distinct from previous findings.

Methods

Matrix to describe node positions

QMF is an individual-based mean-field method, where the adjacency matrix of the network is integrated to calculate the probability of each individual being in any one of the possible states4. To describe the spreading dynamics on a multilayer network with interlayer travel infections, we define a supra-adjacency matrix GC of size 4N × 4N to describe the contacts between individuals in the system, which is

$${G}_{C}=\left[\begin{array}{llll}{G}_{A}&0&0&0\\ 0&{G}_{E}&0&0\\ 0&0&{G}_{E}&0\\ 0&0&0&{G}_{B}\end{array}\right],$$

where GA and GB are the adjacency matrices characterizing the contacts in layers A and B, respectively, and GE is the contact matrix of travelers during the trip [eij = 1 if both i and j (i ≠ j) are travelers, otherwise eij = 0]. Different from a network adjacency matrix, cij in matrix GC represents the possible contact between the individuals at positions i and j. These positions can be the nodal positions in layers A and B, and they can also be on the interlayer edges A → B and B → A. Specifically, \(i\in \left[1,N\right]\) indicates that it is a nodal position in layer A, \(i\in \left[N+1,2N\right]\) signifies that the node is located on the interlayer edge A → B, \(i\in \left[2N+1,3N\right]\) specifies a node on the interlayer edge B → A, and \(i\in \left[3N+1,4N\right]\) gives that the node is in layer B. For the travelers to form the contact network on the trip, they must have the same travel age and directions (the distribution of the travelers at different locations is analyzed in Supplementary Note 8). The average degree of the contact network depends on the total number of travelers, the contact ability and the travel time, as stipulated by Eq. (S3).

To describe the impacts of travel behaviors of individuals, we define the following travel matrix GH:

$${G}_{H}=\left[\begin{array}{llll}-{G}_{T}&0&{G}_{T}&0\\ {G}_{T}&-{G}_{T}&0&0\\ 0&0&-{G}_{T}&{G}_{T}\\ 0&{G}_{T}&0&-{G}_{T}\end{array}\right],$$

where each row of the matrix quantifies the travel-induced change (due to the departure and arrivals of the travelers) in the active nodes at the nodal positions in layer A, trip from A to B, trip from B to A, and the positions in layer B, respectively. The matrix GT is diagonal with the size N × N, where tii = 1 if node i is a traveler, otherwise tii = 0. Let Hi,j denote the elements of GH. The relation H1,1 = − GT means that the departure of travelers from layer A will reduce the number of active nodes in layer A, and H1,3 represents that travelers along the interlayer edge B → A to layer A will increase the number of active nodes in layer A. Similarly, H2,2, H3,3 and H4,4 represent the decrease in the active nodes due to the departure of travelers from A → B, B → A and layer B, respectively, and H2,1, H3,4 and H4,2 represent the increase in the active nodes due to the arrival of the travelers at A → B, B → A and layer B, respectively. To facilitate the derivation of the dynamical equations and theoretical analyses, we divide GH into two matrices: GF and GD given by

$${G}_{F}=\left[\begin{array}{llll}0&0&{G}_{T}&0\\ {G}_{T}&0&0&0\\ 0&0&0&{G}_{T}\\ 0&{G}_{T}&0&0\end{array}\right],$$

and

$${G}_{D}=\left[\begin{array}{llll}-{G}_{T}&0&0&0\\ 0&-{G}_{T}&0&0\\ 0&0&-{G}_{T}&0\\ 0&0&0&-{G}_{T}\\ \end{array}\right].$$

Spreading dynamics in multilayer network with Markovian travel

We define si(t), ρi(t) and ri(t) as the probabilities of a position i holding an individual being in state S, I and R at time t, respectively, where i represents one of the nodal positions in layer A, A → B, B → A and layer B, as in matrices GC and GH. Permanent residents stay in one of the layers, and travelers can be in one of the four possible positions. Let pi be the probability of the nodal position i being active (an individual is actually there). The details involved in the calculation of pi can be found in Supplementary Note 8. As an individual can be in one of the three possible disease states, we have si(t) + ρi(t) + ri(t) = pi. As the individuals within the layers and on the travel process have different spreading dynamics, we divide the nodes into two groups: \({{{\Omega }}}_{L}=\left\{i\left\vert i\in [1,N]\cup [3N+1,4N]\right.\right\}\) and \({{{\Omega }}}_{E}=\left\{i\left\vert i\in [N+1,3N]\right.\right\}\), representing, respectively, the sets of nodes within layers and on the interlayer edges. The set of differential equations describing the spreading dynamics in the multilayer system with Markovian travel infections can then be written as

$$\frac{d{s}_{i}(t)}{dt}=\left\{\begin{array}{ll}&-{s}_{i}^{}(t){\lambda }_{i}(t)+q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t)\\ &+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t),\,i\in {{{\Omega }}}_{L};\\ &-{s}_{i}^{}(t){\lambda }_{i}(t)+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t)\\ &+q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t),\,\,i\in {{{\Omega }}}_{E},\end{array}\right.$$
(1)
$$\frac{d{\rho }_{i}(t)}{dt}=\left\{\begin{array}{ll}&{s}_{i}^{}(t){\lambda }_{i}(t)-\mu {\rho }_{i}^{}(t)+q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right]\\ &+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right],i\in {{{\Omega }}}_{L};\hfill \\ &{s}_{i}^{}(t){\lambda }_{i}(t)-\mu {\rho }_{i}^{}(t)+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right]\\ &+q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right],i\in {{{\Omega }}}_{E},\hfill\end{array}\right.$$
(2)
$$\frac{d{r}_{i}(t)}{dt}=\left\{\begin{array}{ll}&\mu {\rho }_{i}^{}(t)+q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right)\\ &+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right),\,i\in {{{\Omega }}}_{L};\\ &\mu {\rho }_{i}^{}(t)+\frac{1}{{t}_{T}}\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right)\\ &+q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right),\,\,i\in {{{\Omega }}}_{E}.\end{array}\right.$$
(3)

The first term on the right side of Eq. (1) for i ∈ ΩL represents the nodes being infected by neighbors within the layers, the second term represents the decreases in si due to the departure of the S-state travelers, and the third term describes the increase in si due to the arrival of the S-state travelers. In these equations, q is the travel rate of travelers starting from a layer, and 1/tT is the rate of travelers jumping instantaneously from the interlayer edges to a layer. Similarly, for i ∈ ΩE in Eq. (1), the first term represents the change in the S-state nodes due to the infection on the interlayer edges, and the second and third terms, respectively, describe the change in the S-state nodes due to the departure of travelers from the interlayer edges and the arrival of the travelers at the interlayer edges. Equations (2) and (3) describe the dynamics of the infected and recovered nodes, respectively. The probability λi(t) of an individual being infected by its neighbors at node i at time t is given by

$${\lambda }_{i}(t)=\left\{\begin{array}{ll}1-\mathop{\prod }\limits_{j=1}^{4N}\left(1-\beta {c}_{ij}{\rho }_{j}^{}(t)\right),&i\in {{{\Omega }}}_{L};\\ 1-\mathop{\prod }\limits_{j=1}^{4N}\left(1-\frac{1}{{t}_{T}}\alpha \beta {c}_{ij}{\rho }_{j}^{}(t)\right),&i\in {{{\Omega }}}_{E}.\\ \end{array}\right.$$
(4)

We have derived the analytical epidemic thresholds using the Jacobian matrix method (Supplementary Note 9).

Spreading dynamics in multilayer network with non-Markovian travel process

Let \({s}_{i}^{l}(t)\), \({\rho }_{i}^{l}(t)\) and \({r}_{i}^{l}(t)\) be the probabilities of i (i ∈ ΩE) with travel age l being in the state of S, I, R at time t, respectively. The spreading dynamics in the multilayer system with non-Markovian process can be described as follows.

For i ∈ ΩL, we have

$${s}_{i}^{}(t+{{\Delta }}t)= \,\left(1-{\lambda }_{i}(t)\right){s}_{i}^{}(t)\\ +q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t)\\ +\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left(1-{\lambda }_{j}^{{t}_{T}-{{\Delta }}t}(t)\right){s}_{j}^{{t}_{T}-{{\Delta }}t}(t);$$
(5)
$${\rho }_{i}^{}(t+{{\Delta }}t)= \,\left(1-\mu \right){\rho }_{i}^{}(t)+{s}_{i}^{}(t){\lambda }_{i}(t)\\ +q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right]\\ +\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{{t}_{T}-{{\Delta }}t}(t)\right.\\ \;\left.+{s}_{j}^{{t}_{T}-{{\Delta }}t}(t){\lambda }_{j}^{{t}_{T}-{{\Delta }}t}(t)\right];$$
(6)
$${r}_{i}^{}(t+{{\Delta }}t)=\, {r}_{i}^{}(t)+\mu {\rho }_{i}^{}(t)\\ +q\mathop{\sum }\limits_{j=1}^{4N}{d}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right)\\ +\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left({r}_{j}^{{t}_{T}-{{\Delta }}t}(t)+\mu {\rho }_{j}^{{t}_{T}-{{\Delta }}t}(t)\right),$$
(7)

where the first term on the right side of Eq. (5) represents the S-state nodes not being infected, the second term captures the departure of susceptible travelers from the layers, and the third term describes the arrival of susceptible travelers with travel age l = tT − Δt at the previous time step. Similarly, Eqs. (6) and (7) describe the spreading dynamics of the I and R nodes, respectively.

For i ∈ ΩE: we have

$${s}_{i}^{l}(t+{{\Delta }}t)=\left\{\begin{array}{ll}&(1-{\lambda }_{i}^{l-{{\Delta }}t}(t)){s}_{i}^{l-{{\Delta }}t}(t),\hfill\\ &l={{\Delta }}t,2{{\Delta }}t,\ldots ,{t}_{T}-{{\Delta }}t;\hfill \\ &q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left(1-{\lambda }_{j}(t)\right){s}_{j}^{}(t),l=0;\\ &0,l\ge {t}_{T},\hfill \end{array}\right.$$
(8)
$${\rho }_{i}^{l}(t+{{\Delta }}t)=\left\{\begin{array}{ll}&(1-\mu ){\rho }_{i}^{l-{{\Delta }}t}(t)+{\lambda }_{i}^{l-{{\Delta }}t}(t){s}_{i}^{l-{{\Delta }}t}(t),\hfill\\ &l={{\Delta }}t,2{{\Delta }}t,\ldots ,{t}_{T}-{{\Delta }}t;\hfill \\ &q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left[\left(1-\mu \right){\rho }_{j}^{}(t)+{s}_{j}^{}(t){\lambda }_{j}(t)\right],l=0;\hfill \\ &0,l\ge {t}_{T},\hfill \end{array}\right.$$
(9)
$${r}_{i}^{l}(t+{{\Delta }}t)=\left\{\begin{array}{ll}&{r}_{i}^{l-{{\Delta }}t}(t)+\mu {\rho }_{i}^{l-{{\Delta }}t}(t),\hfill \\ &l={{\Delta }}t,2{{\Delta }}t,\ldots ,{t}_{T}-{{\Delta }}t;\hfill \\ &q\mathop{\sum }\limits_{j=1}^{4N}{f}_{ij}\left({r}_{j}^{}(t)+\mu {\rho }_{j}^{}(t)\right),l=0;\\ &0,l\ge {t}_{T}.\hfill \end{array}\right.$$
(10)

The first case described by Eq. (8) means that the probability of node i in the S-state at time t + Δt depends on that of the previous time step, where the current travel age of the travelers is l and their travel age at the previous time step is l − Δt. The second case in Eq. (8) is that the travelers are about to start their trip with the travel age l = 0. The third case is where, when the travel age is equal to or greater than the travel time between the layers, the travelers return to the layers and are not on the interlayer edge. Equations (9) and (10) describe the dynamics of I nodes and R nodes in a similar way.

The probability λi(t) of an individual being infected at node i in layers by its neighbors at time t is

$${\lambda }_{i}(t)=1-\mathop{\prod }\limits_{j=1}^{4N}\left(1-\beta {c}_{ij}{\rho }_{j}^{}(t)\right),i\in {{{\Omega }}}_{L},$$
(11)

and the probability of a traveler with travel age l being infected at node i on the interlayer edge at time t is

$${\lambda }_{i}^{l}(t)\, =\, 1-\mathop{\prod }\limits_{j=1}^{4N}\left(1-\alpha \beta {c}_{ij}{\rho }_{j}^{l}(t)\right)\\ ,i\in {{{\Omega }}}_{E}\,and\,l={{{{{{{\rm{0}}}}}}}},{{\Delta }}t,\ldots ,{t}_{T}-{{\Delta }}t.$$
(12)

The number of dynamical equations required to model the spreading dynamics with non-Markovian travel depends on the value of tT/Δt.