Introduction

The world’s annually rising primary energy consumption1,2 correlates with increasing CO2 emissions and climate change3. Meeting the demand while reducing emissions requires scientific research, industrial production, and finally, a very large installation volume of environmentally friendly electricity generation technologies4. Thin-film solar modules for photovoltaic energy generation combine high cell efficiencies5,6,7, short energy payback times due to low consumption of energy and active material8,9, and potential for cheap monolithic and large-scale manufacturing at moderate temperatures10,11,12. Further advantages like integration into efficient tandem applications13,14,15,16, their possibility for ink-based fabrication techniques17, their application in photoelectrochemical (PEC) hydrogen production14,18,19, and the feasibility for flexible substrates13,20,21,22 make thin-film technology a promising candidate for many different applications.

In order to keep pace with the current market-dominating c-Si technology23,24, thin-film technologies need to have comparably high efficiencies. The best way to systematically analyze the internal physical processes is automated computer-aided modeling approaches25. Therefore, thin-film solar devices are under frequent investigation by computer simulation, both by electrical simulations26,27,28 as well as by drift-diffusion models29,30. To not only guide development efforts towards increased efficiencies but also to higher net energy yields, entire modules in the field need to be investigated instead of single cells in the laboratory31,32. Real-world simulations identify, allocate, quantify, and rate all loss mechanisms within thin-film solar modules. It is important to put in proportion all identified losses33. Hence, a holistic simulation method including all loss mechanisms from the Shockley–Queisser model34,35 down to the actual produced module power is necessary. This requires a linkage of at least three simulation levels, as realized in this unique simulation platform. Therefore, we connected an electronic drift–diffusion model29 within a one-dimensional finite element method for the semiconductor material simulation, a modified transfer-matrix approach36,37 to consider the optics with partially incoherent interference due to rough interfaces38, and an electrical Poisson’s equation39 solver embedded into a quasi-three-dimensional finite element method using a Delaunay-triangulated mesh40,41 to account for the electrical module behavior. Therefore, our methodology includes the entire chain of physical processes within the simulation of solar modules and bridges the gap between cell simulation and system design software. All simulations are programmed by the authors without using any external software. This holistic approach also allows a calculation in the backward direction and therefore allows the inference of material parameters from characteristic curves on the module level, which we will call Reverse Engineering Fitting (REF)40. Moreover, our methodology comes with the additional benefit that possible research improvements can be checked for their contribution to the overall module performance, revealing insightful sensitivity analyses. Furthermore, solar power plant operators often face the question of financial return. While the investment costs in €per kWp can be calculated easily, the yield per time in kWh per a depends e.g., on the climate conditions of the specific system location. Advanced simulation techniques like this work offer the possibility to calculate such quantities. Furthermore, the effect of technological improvements can be evaluated much better, and therefore, priorities can be set in the research and development process.

In the photovoltaic market, there is a wide variety of different technologies. While silicon wafer-based photovoltaic is widespread, thin-film systems have great potential for cost-effective energy generation. Thin-film modules with the monolithic interconnection technique are more difficult to simulate than wafer-based modules. Our simulation methodology works for all thin-film technologies and, in principle, could be modified for wafer-based technologies. We demonstrate our universal approach on the 1.2 × 0.6 m2 large copper indium gallium diselenide CuIn1−xGaxSe2 (CIGS) module N-G1000E105 from NICE Solar Energy GmbH. It consists of 144 monolithically integrated cells and the following layer stack: 400 nm molybdenum (Mo)/2100 nm CIGS/50 nm cadmium sulfide (CdS)/50 nm intrinsic zinc oxide (i-ZnO)/800 nm aluminum-doped zinc oxide (AZO)/750 μm encapsulant film/3.2 mm top side ARC-coated low-iron solar float glass.

In this paper, we demonstrate a holistic approach to simulate solar modules under real conditions. We use a combination of an optical transfer matrix method, an electrical transport simulation, and a drift–diffusion calculation. This allows top-down loss analyses, determining the influence of possible future technology improvements on the yield, and backward calculations from measured data to difficult-to-measure parameters.

Results

Evolving the digital model and its parameters under standard testing conditions (STC)

As a first step, all measurable quantities are implemented into the model. This mainly includes geometrical data (layer thicknesses and lateral dimensions), complex refractive indices of all thin-film layers and from the encapsulant layer (for CIGS from literature, for all remaining materials fitted ellipsometry and transmittance measurements), as well as specific resistivities of all contact layers (here AZO and Mo). While there are also other optical data for CIGS in literature42, we used the data from43, since we found a very good agreement of simulated and measured external quantum efficiencies. Moreover, a sensitivity analysis reveals that the exact absorption coefficient of the CIGS layer is not very sensitive for a sufficiently large layer thickness if the band gap matches the experimental value. To properly execute drift-diffusion simulations, several semiconductor parameters of the photo-active layers from the literature are implemented as well. They are listed in Table 1.

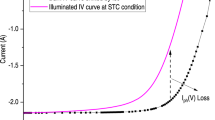
Table 1 Semiconductor parameters for drift-diffusion modeling. The material abbreviations CIGS, CdS, i:ZnO, and AZO stand for copper indium gallium diselenide, cadmium sulfide, intrinsic zinc oxide, and aluminum-doped zinc oxide, respectively. All bold numbers are fitted via reverse engineering fitting procedure from the measured module I-V characteristic, all others are adapted from literature. The CIGS absorber material has a linear grading within the ratio of gallium to gallium and indium concentrations [Ga]/([Ga]+[In]) (GGI) of 0.2 to 0.4. Detailed conversions into an absorber band gap can be found in Supplementary Note 1 and band gap or in literature69,70.
Full size table

In Fig. 1, the black points represent the measured current–voltage (I–V) characteristic of the module, broken down into a single monolithically integrated cell. The consistently equal shunting effect up to the 0.5 V range without having a larger slope at higher voltages reveals the homogeneity of all cells within the module44. Otherwise, a dip in the current could be seen at higher voltages45. It justifies the approach of a sufficiently homogeneous p–n junction without pronounced hot-spot shunt regions in individual cells.

Fig. 1: All relevant I–V characteristics from Shockley–Queisser model to the actual module curve.
figure 1

The gray curve is the I–V characteristic of the Shockley-Queisser model for the band gap of the used module (1.13 eV). After performing a stand-alone drift–diffusion simulation with the parameters from Table 1, we end up at the red curve. The blue curve arises after further subtracting all optical losses and represents the infinitesimal small cell level. For the green curve, we included all geometrical losses of the module, and the orange curve emerges after electrical stimulation and represents the final result for the module I–V characteristic of the stacked simulation. It has a power conversion efficiency (PCE) of 14.3%. The black dotted curve shows actual measurements of the module.

Full size image

After we accounted for the electrical, geometrical, and optical losses (orange, green, and blue curves), we performed a Reverse Engineering Fitting (REF) procedure40 for all difficult-to-measure parameters at standard testing conditions (STC) (meaning 1000 W m−2 irradiance, 25 °C module temperature, and AM1.5G spectral distribution) throughout all simulation levels down to the drift-diffusion model. These parameters are the donor and acceptor densities and electron and hole mobilities. More information about the REF procedure can be found in the methods section. Using this multi-level REF method, we are able to determine the quantities of donor and acceptor densities and the charge carrier mobilities within the CIGS and CdS layers, which are experimentally difficult to access. These results can be seen as bold numbers in Table 1. The fitted donor density within the CdS and the acceptor density within the CIGS turn out to be on a comparable level with values found in literature46,47,48,49,50 within the \(1{0}^{17}\,\frac{1}{{{{{{{{{\rm{cm}}}}}}}}}^{3}}\) and \(1{0}^{15}\,\frac{1}{{{{{{{{{\rm{cm}}}}}}}}}^{3}}\) range, respectively. However, we found evidence for a noticeably higher electron mobility within the CIGS layer of \({\mu }_{{{{{{{{\rm{e}}}}}}}}}=200\,\frac{{{{{{{{\rm{cm}}}}}}}}}{{{{{{{{\rm{V}}}}}}}}\,{{{{{{{\rm{s}}}}}}}}}\) instead of the commonly used value of \(100\,\frac{{{{{{{{\rm{cm}}}}}}}}}{{{{{{{{\rm{V}}}}}}}}\,{{{{{{{\rm{s}}}}}}}}}\)47,48,49,50,51, which is often just a estimation in a plausible order of magnitude since a reasonable measurement is rather difficult to execute. This results in a higher electron diffusion length \({L}_{{{{{{{{\rm{e}}}}}}}}}=\sqrt{{\mu }_{{{{{{{{\rm{e}}}}}}}}}\tau {k}_{{{{{{{{\rm{B}}}}}}}}}T/{q}_{{{{{{{{\rm{e}}}}}}}}}}\) at a given temperature T, a charge carrier lifetime τ, the Boltzmann constant kB, and the electron charge qe.

In summary, we developed a holistic model of a real-world solar module accounting for all dominant loss mechanisms by combining an electronic drift-diffusion model within a one-dimensional finite element method (FEM), an optical transfer-matrix model (TMM), and a quasi-three-dimensional FEM solving the electrical Poisson’s equation. All models are described in more detail in the methods section and in Supplementary Note 2. The models are fed by experimentally measured data, data from the literature, and reverse engineering fitted data. This entirely holistic model enables us to calculate from the Shockley–Queisser limit34 of the 1.13 eV CIGS absorber down to the module level.

Figure 1 shows the I–V characteristics under STC of all intermediate steps. While the short-circuit current density jsc remains constant within the drift-diffusion simulation from the Shockley-Queisser model to the semiconductor level, the open-circuit voltage Voc is drastically decreased due to non-radiative recombination52, which is even the case for high-performance cells53. The optical TMM simulation reduces jsc due to reflection and parasitic and incomplete absorption. Since Voc logarithmically depends on the photocurrent, it is slightly decreased as well. This blue line is often referred to as the cell level since only vertical optoelectronical effects and no lateral transport effects are considered to this point. To account for the module geometry, edge areas and interconnect areas are introduced, generating the green curve. The new I–V curve is calculated via a comparison of the active and inactive areas. Finally, the current collection and transport are taken into account by the quasi-three-dimensional Poisson’s equation solver. This mainly increases the series resistance and the shunt, yielding a lower fill factor. Moreover, the short-circuit current density is reduced. This is due to the effect of additional shunting resistance and local maximum power point (MPP) mismatches54. The latter arises from a non-equal voltage distribution across the cell. This leads to different points of operation within the material’s I-V characteristic for different spatial locations, and only a minority of them are exactly at the cell’s MPP40.

The finally predicted I–V characteristic under STC (orange curve in Fig. 1) has a coefficient of determination of 0.997 with respect to the experimentally measured I-V curve (black dots), revealing the high accuracy of our model.

Applying meteorological data to the model

In order to simulate the daily yield of the module, the incoming irradiance and the module temperature (measured on the rear side of the module) need to be considered. Their course over the day can be seen in Fig. 2. We chose September 9, 2020 as a sample day because it was a clear day with no clouds. The dip at the left of the irradiance graph (black line) at half past 7 arises from locally present trees that cover the low sun at low altitudes in the morning. The module temperature (blue–red line) roughly follows the behavior of the irradiance with a certain delay due to heating.

Fig. 2: External conditions on the solar module during the daytime of September 9, 2020.
figure 2

The irradiance (black line) on the module plane has basically a trigonometrical dependence on the time of day. The drop from 6 am to 7:30 am is due to trees that block the sunlight. The measured module temperature (blue-red line) has the same behavior as the irradiance but lags behind it.

Full size image

The effect of the module temperature mainly influences the semiconductor properties within the p–n junction. Therefore, we simulated the p–n junction without lateral electrical effects at different temperatures and the resulting temperature-dependent I–V characteristic acts as the input for the subsequent Poisson’s equation solver. Figure 3 shows the dependence of the open-circuit voltage and the fill factor as a function of the temperature. The solid lines represent the p–n junction simulation results, which are exclusively generated by the drift-diffusion model, whereas the dashed lines represent the overall module behavior, including all three simulation levels. The decreasing behavior of Voc and FF with rising temperature can be explained by the increasing intrinsic carrier concentration, which is mainly due to the enhanced thermal generation of electron–hole pairs55. The short-circuit current is hardly affected by the temperature variation, as can be seen in Supplementary Note 3. These findings agree with previous research and practical experience56,57. Since all temperature dependencies are nearly linear, temperature coefficients can be determined. Our simulation reveals values of −2.0 mV K−1 and −0.06% K−1, which are in agreement with measured values of −2.1 mV K−1 and −0.05% K−156 and theoretical models (−1.6 mV K−1 and −0.015% K−1)58. The detailed calculation of the theoretical values is available in Supplementary Note 3.

Fig. 3: Simulated temperature-dependence of the open-circuit voltage and the fill factor.
figure 3

The solid line represents the results of the drift–diffusion calculation without any optical and electrical losses, while the dashed line shows the overall module behavior. The rising temperature increases the intrinsic carrier concentration and decreases the band gap, which leads to the observed decreasing behavior of the open circuit voltage and the fill factor. The temperature dependence of the short circuit current density and power conversion efficiency can be found in Supplementary Note 3.

Full size image

The drift-diffusion model is thus calculated with the measured temperature conditions shown in Fig. 2. The corresponding irradiance conditions are fed into the transfer matrix calculation. Finally, Poisson’s equation solver is applied to generate the resulting solar-module parameters, which are plotted as orange lines in Fig. 4, together with the experimentally determined data (black dotted). The precise prediction of all three quantities reveals an accurate, holistic model on all three simulation levels.

Fig. 4: Solar-module parameters during the daytime of September 9, 2020.
figure 4

The numbers on the right axis are cell values that are calculated from the module and the number of cells, while the actual measurement data of the module belongs to the left axis. While the open-circuit voltage Voc stays rather constant, the short-circuit current jsc nearly linearly follows the irradiance curve. The drops in the fill factor FF in the morning and evening can be explained by a low generation current, and the saddle at noontime is due to a high temperature and a huge current density.

Full size image

Several features within the data can be understood and explained by the use of the three-stage simulation model. The open-circuit voltage is mainly constant throughout the entire day. However, for very low irradiation intensities, Voc does drop due to its logarithmic dependence on the photocurrent. A prominent feature is the increased Voc in the morning compared to the almost constant value of 95 V for the rest of the day. This can be explained by a low module temperature in the morning. After half past 7, an abrupt increase in irradiance due to sunlight emerging from behind the trees leads to a comparably high current while still maintaining a low module temperature. The result is an increased open-circuit voltage, which relaxes and plateaus while the thermal equilibrium is reached.

The short-circuit current basically follows the behavior of the irradiance curve in Fig. 2 due to its linear dependence within the transfer-matrix method. This is represented in the simulated data as well as in the experimental data. The dip in the morning due to shadowing by nearby trees is clearly visible within this jsc graph again.

A notable feature in the plotted fill factor in graph c) is the drop in the early morning and late evening hours. This is due to the low irradiance at this time, which leads to comparably low photocurrents in contrast to the permanently present shunting currents. The dip around noontime is due to two effects. Firstly, according to Fig. 3, the fill factor drops at the higher temperatures present within this time frame. Secondly, the high irradiance at noon implies high current densities. Since the conductivities of the contact layers hardly change with temperature, high currents result in a large potential gradient according to Ohm’s law, which is always associated with large electrical losses and hence a lower fill factor.

We studied the same solar-module parameters for a cloudy day (September 6, 2020), which has a much more spiky temperature and illumination behavior throughout the day. Results for this day can be found in Supplementary Note 4. Despite the irregular profile of the operating conditions, we are able to predict Voc, jsc, and FF and, therefore, the generated power with high accuracy.

Holistic loss analysis from theoretical efficiency limit to actual module yield

All relevant loss mechanisms that can occur within homogeneous thin-film solar modules are illustrated in Fig. 5. We classified them into four different categories: semiconductor losses, optical losses, geometrical losses, and electrical losses. Each of these classes corresponds to one of the four simulations and calculations described in the section above and illustrated in Fig. 1. While all intrinsic material losses are due to recombination, optical losses can be split into reflection, incomplete absorption (transmission), and parasitic absorption. Their detailed values are determined by the exact number of reflected and absorbed photons within the transfer-matrix approach. Geometrical losses are subdivided into edge area losses, and dead area losses within the monolithic interconnect and can be easily calculated via comparison of areas. Electrical losses have the largest variety by being split into ohmic losses within all contact layers and module transitions, local MPP mismatches, and shunts across P1 and P3 gaps. All ohmic losses and shunts can be calculated by Ohm’s law. The local MPP mismatch is given as the difference of the hypothetically possible produced power without any voltage distribution (each finite element at MPP) and the sum of all actually produced powers of all finite elements54.

Fig. 5: Possible losses within a thin-film solar module.
figure 5

The losses are divided into four categories. Reflection, parasitic absorption, and incomplete absorption form the optical part. Recombination mechanisms are within the electronic portion, while area losses represent the geometrical losses. Electrical losses can be classified into ohmic losses, shunts, and local maximum power point mismatches.

Full size image

The upper curve in Fig. 6 is determined from the Shockley-Queisser model34 via the illumination and the temperature behavior from Fig. 2 and the module area of 1.2 × 0.6 m2 with 144 individual cells. It describes the theoretical maximum power that could be achieved under ideal conditions. For each time step, a coupled simulation of the drift–diffusion model, transfer-matrix method, geometrical calculation, and Poisson’s equation solver is performed, and all losses are allocated and quantified. The different colorings in Fig. 6 show the assignment of each loss mechanism. We define the absolute limit of the material as the Shockley–Queisser power minus the recombination losses. This is the maximum power that could be achieved by an optically and electrically ideal module. However, a more realistic limit is an infinitesimally small cell, which contains all optical losses but does not suffer from any electrical transport effects or module area losses. This efficiency limit is at the bottom line of the blue area. Finally, extending a tiny cell towards a real-world module introduces geometrical losses (green) and electrical losses (orange) due to its two-dimensional expansion. Therefore, after subtracting all losses from the Shockley–Queisser limit to the module level, we predict the module to produce the gray colorized area as power output. Integrating over the entire day, we calculate that the module will produce 698.9 Wh. Experimental, time-resolved power measurements during the day are plotted as black dots, and the integrated yield is calculated to 698.7 Wh for the entire day, which is in remarkable agreement with the predicted simulated value. This equals a gain of 6.8 kWh per day ⋅ kWp for the considered day. Since this was a perfect summer day, this value would be much lower for a simulation over an entire year.

Fig. 6: Shockley–Queisser model, loss analysis and generated module power during daytime of September 9, 2020.
figure 6

The material abbreviations CdS, i:ZnO, and AZO stand for cadmium sulfide, intrinsic zinc oxide, and aluminum-doped zinc oxide, respectively, MPP is the maximum power point, and P1, P2, and P3 are the interconnecting trenches between to serially connected cells. The upper edge of the red area represents the Shockley-Queisser limit for a band gap of 1.13 eV adapted for the module size and the prevailing illumination and temperature. After all losses are identified and quantified, the module is predicted to produce the power indicated within the gray area. Actual measurements in the field are marked as black dots.

Full size image

We conclude that with this three-stage simulation model, we are able to accurately simulate real-world thin-film solar modules with all their external influences like temperature and different illumination scenarios and even allocate all losses to their origins.

To put these results in perspective, we compared the resulting power conversion efficiency (PCE)

$${{{{{{{\rm{PCE}}}}}}}}=\frac{{P}_{{{{{{{{\rm{MPP}}}}}}}}}}{{P}_{{{{{{{{\rm{in}}}}}}}}}}=\frac{{V}_{{{{{{{{\rm{MPP}}}}}}}}}{{\cdot }}{I}_{{{{{{{{\rm{MPP}}}}}}}}}}{{P}_{{{{{{{{\rm{in}}}}}}}}}}$$
(1)

with the light input power Pin and the MPP voltage VMPP, current IMPP, and power PMPP of the module with the PCE calculated from the Shockley–Queisser model. Figure 7a shows a colormap of the Shockley–Queisser limit with a band gap of 1.13 eV for a given temperature and irradiance. As can be seen, the Shockley–Queisser model is a variable limit depending on certain input parameters rather than a fixed efficiency limit. As a matter of fact, the PCE limit changes from 29% up to 34%, even within these realistic non-STC conditions. The black line with the blue points represents the trajectory of the operating conditions on the module in the course of the analyzed day September 9, 2020. The projection of the Shockley–Queisser PCE is plotted in Fig. 7b) as a function of time during the day. As in Fig. 6, all losses (colored areas) and the measured module PCE (black dotted) are plotted as well. Since all solar-module parameters in Fig. 4 are simulated accurately, the simulated and measured PCE match quite well.

Fig. 7: Trajectory of the operating conditions of the module within the Shockley–Queisser model during the daytime of September 9, 2020.
figure 7

The Shockley–Queisser limit for a band gap of 1.13 eV is plotted as a colormap in graph a) as a function of temperature and irradiance. The black line represents the course of the conditions during the considered day. The same curve is shown in graph b) in combination with the actual module power conversion efficiency (PCE). All loss mechanisms have the same color coding as in Fig. 6.

Full size image

Low-light conditions in the early morning and late evening hours and heating up around noontime reduce the actual module PCE disproportionately more than the Shockley–Queisser PCE. This can be attributed to the shunt resistances and high temperature coefficients, respectively. Since the PCE is a relative quantity, the simulated values in the early morning and late evening hours don’t exactly align with the measured values, but the absolute errors for low intensities are actually extremely small. Moreover, a physical error source might be the absence of a spatially distributed thermal model59 and assuming a constant equilibrium temperature for the entire module. Since the temperature measurement was performed on the rear side of the module, the actual temperature of the p–n junction might change by up to around 2 K. A loss analysis for laboratory-controlled standard testing conditions can be found in Supplementary Note 5.

Possible improvements on the module level

There are many suggestions and realizations of how to improve the light-absorbing material30,60,61,62,63,64,65,66 and, therefore, the entire module performance. Since the largest single source of loss is recombination, it is reasonable to direct research efforts in this direction. However, this section has its focus on improvements on the module level without touching the absorber material at all. It shall serve as a sensitivity analysis to get a feeling for which parameters have a significant effect on the results and are, therefore, prime targets for future optimization efforts. Many improvements are conceivable, even on complex topological issues like grid pattern optimization32,67. However, here we focus on the following points: Reducing sheet resistance in the TCO contact layer, reducing optical absorption in the TCO contact layer, reducing optical absorption in the encapsulant, reducing edge areas, and reducing interconnect areas. As noted in Fig. 1, the actual PCE at STC of the module is 14.27%. In this section, we look for methods to get a PCE gain of 0.65% and hence to 14.92%.

To gain this improvement by reducing electrical losses within the front TCO layer, we can use our simulation to calculate the necessary improvement. We come up with a required TCO sheet resistance of 7.75 Ω instead of the actual 25 Ω for the same grid resistivity. Alternatively, the optical losses can be addressed. To achieve the required 0.65%, either the front TCO needs to absorb around 26% less within the relevant wavelength range, or the encapsulant is not allowed to have any parasitic absorption at all. Another way is to reduce the edge area from around 505 cm2 (7% of the total module) to around 190 cm2 (2.6% of the total module). The same effect can be achieved by reducing the interconnect area by the same factor from 265 μm in width to 100 μm. To do so, we need to adapt the cell width, as can be seen in Table 2. For the 265 μm of total interconnect width used in the design of our reference module, the cell width is optimized to around 4 mm. However, for 100 μm, the cell width needs to be reduced to 3.5 mm to minimize ohmic losses. Implementing all of the five improvement suggestions mentioned above would improve the efficiency even more than five times 0.65%. In fact, the resulting module would have a PCE of 17.9%, without modifying the CIGS deposition process. This overlap is due to the interactions of the positive effects. For example, a more conductive contact layer material allows the cell to be 4.2 mm in width despite the smaller interconnect area.

Table 2 Comparison of ideal cell widths and efficiencies for different improvement implementations described in the main text. In the first row, the standard reference module is used, while in the second row, only the interconnect area was reduced, and in the last row, all improvements are implemented (sheet resistance and transmittance of the transparent conductive oxide (TCO) layer, encapsulant transmittance, interconnect and edge area). All simulated modules have the same area of 1200 × 600 mm2. Therefore, the ideal cell width determines the amount of monolithically interconnected cells and hence the absolute module voltage. All optoelectrical parameters are shown, including the open circuit voltage Voc, short circuit current (density) Isc and jsc, fill factor FF and power conversion efficiency PCE.
Full size table

This work demonstrates that the physical processes within thin-film solar modules in the field under real application conditions can be simulated in one three-staged simulation, including a correction for the inactive areas. The three levels of drift-diffusion model, modified transfer-matrix method, and quasi-three-dimensional finite-element Poisson’s equation solver have been linked—to the best of our knowledge—for the first time in literature. We used geometrically, electrically, and optically measured input data at standard testing conditions (STC) as well as drift-diffusion parameters from the literature. Having established the entire physical model of the module, we can predict solar-module parameters, even for conditions that are far beyond STC, with remarkable agreement. Such simulations can be extended to yield predictions for an entire day based on meteorological data. Due to our holistic device physics, a time-resolved top-down loss analysis from the Shockley–Queisser model to the actual module power can be calculated. Moreover, our sensitivity analysis clearly shows the potential and need for materials with improved optical and electrical properties in order to advance toward higher module efficiencies and to close the gap between cell and module levels. Our reverse engineering fitting (REF) procedure allows us to calculate backward from the module level down to the cell level and even further down to the drift-diffusion level. Parameters that may be difficult to measure experimentally can be determined by this approach.

Methods

Setting up device simulations

In this work, we used multiple simulation methods and link them to each other. This is necessary to achieve a holistic physical model starting from the material parameters up to the module level. Using this multi-level simulation procedure, we are able to describe all environmental influences, from temperature effects up to impacts of different illumination conditions.

For the electronic semiconductor simulation, we used a drift-diffusion model within a one-dimensional finite element method29. This model solves the van-Roosbroeck system, which is formulated as Poisson’s equation inside the semiconductor and the two continuity equations for electrons and holes. To account for the optics, we used a modified generalized transfer-matrix approach36 accounting for partially incoherent interference due to rough interfaces38. This includes a Lambert–Beer-like absorption for each material within the layer stack as well as internal reflections, back-side reflections, and thin-film interference. Finally, the electrical behavior of the solar modules is considered in Poisson’s equation39 solver embedded into a quasi-three-dimensional finite element method using a Delaunay-triangulated mesh40,41. Finite elements with an active area consist of two electrical potentials on the front and back side and a generating current term which is determined by the drift-diffusion simulation. However, elements within the module interconnection do not have a generating current term but consist of large transport resistances (P1 and P3) or an electrical connection from the front to the back contact (P2). A more detailed description of the simulation techniques can be found in Supplementary Note 2.

Reverse engineering fitting (REF)

The routine of REF is a special kind of fitting procedure developed for use with simulations instead of an analytical calculation. Since derivatives for any fitting parameter cannot be calculated in this case, the optimization algorithm must be based on a gradient-free procedure. We used our three-stage simulation approach within the loss function of the optimizer, which requires a long runtime for evaluating the function value. Therefore, the efficiency of the optimization algorithm is mainly due to the number of function evaluations, which is why we used a downhill simplex algorithm68.

The final goal is to match a simulated I-V curve with experimental I-V data, which is given by n experimentally measured voltage-current pairs \(({V}_{i}^{\exp },{I}_{i}^{\exp })\). This is achieved by varying the optimization parameters and revealing a simulated I-V curve with also n voltage-current pairs \(({V}_{i}^{\exp },{I}^{{{{{{{{\rm{sim}}}}}}}}}({V}_{i}^{\exp }))\) via the simulation. The final loss function for the optimization algorithm is the accumulated mean squared error

$${\chi }^{2}=\frac{1}{\mathop{\sum }\nolimits_{i = 0}^{n-1}{w}_{i}}\cdot \mathop{\sum }\limits_{i=0}^{n-1}{w}_{i}\cdot {\left({I}_{i}^{\exp }-{I}^{{{{{{{{\rm{sim}}}}}}}}}({V}_{i}^{\exp })\right)}^{2}$$
(2)

with the the weights wi accounting for non-equidistant voltage steps and an exponential current-voltage dependence. As within conventional optimization algorithms, the input parameters are varied as long as a sufficient accuracy within the loss function is reached. In principle, there can be an arbitrary number of fitting parameters. However, in order to converge in a reasonable time scale, only around 4 to 6 free parameters should be used for the downhill simplex algorithm. The reliability of this method is demonstrated in40.

Coefficient of determination

The coefficient of determination R2 measures the quality of a fit. To determine this quantity, the ratio of the sum of all residual squares with respect to the sum of all total squares are calculated. The exact calculation is given as

$${R}^{2}=1-\frac{\mathop{\sum }\nolimits_{i = 0}^{N-1}{\left({y}_{i}-{p}_{i}\right)}^{2}}{\mathop{\sum }\nolimits_{i = 0}^{N-1}{\left({y}_{i}-\overline{y}\right)}^{2}}$$
(3)

with all N measured values yi, their mean value \(\overline{y}=\frac{1}{N}\mathop{\sum }\nolimits_{i = 0}^{N-1}{y}_{i}\), and the corresponding predicted value pi.

Characterization and measurements

Experimental data have been collected from an N-G1000E105 CIGS module exposed outdoors at the ZSW test field Widderstall located at 09.713°N, 48.536°E, and 750 m above sea level. It was mounted facing south with a fixed tilt angle of 40° without any tracking. The module was individually characterized in the laboratory by I–V curve measurement at STC with a class AAA solar flash simulator. During the exposition, I–V curve scans of the module was conducted and recorded continuously at 1 min intervals by an individual electronic load, which operated the module at MPP between the scans. The plane of array irradiance measurement was performed with a secondary standard pyranometer while the module temperature was measured with a PT1000 resistive sensor at the rear glass surface of the module.

Module geometry

The used module has a spatial dimension of 1200 mm × 600 mm. Along the short side, it has an edge area of 19 mm and 9 mm on the top and bottom sides, respectively. The long side is framed by 14.4 mm of edge and contact area on both sides. The active area of 6695 cm2 is split into 144 monolithically interconnected cells, with 265 μm of interconnect width between the cells. Therefore, all cells are 1172 mm in height and 4 mm in width. The total inactive edge and contact area can be calculated to be 505 cm2, which corresponds to around 7% of the total module area.