Introduction

Combinatorial optimization is ubiquitous and fundamental in many areas of science, engineering, finance, and social networks1. Many optimization problems, such as the traveling salesman problem2,3, the graph coloring problem4, the Boolean satisfiability problem5, spin glass dynamics6,7, protein folding6, etc., belong to the non-deterministic polynomial time (NP) hard or NP-complete class which can be formulated as finding the ground states of Ising spin models8,9. Because of the computational complexity, it is usually challenging to find the exact solutions of general Ising models with traditional electronic computers10,11,12,13. In the past years, many physical systems including the superconducting circuits14, stochastic nanomagnets15,16, trapped ions17, complementary metal-oxide semiconductor devices18, injection-locked laser networks19, polariton condensates20,21, etc., have been applied to realize an Ising simulator and to solve the optimization problems with heuristic search algorithms22,23,24,25,26.

Among these physical implementations, optical Ising machines are particularly attractive because of their capability of parallelism, low energy consumption, and operation at the speed of light25,27,28,29,30,31,32. In addition to the promising approach based on a network of degenerate optical parametric oscillators12,33,34,35, optical Ising machines based on spatial light modulators (SLM) and Fourier optics are also being actively pursued in the optical community30,36,37,38,39,40,41. By encoding the spins in the SLM-modulated binary phase of an incident beam and measuring the light intensity at the focal plane, a fully connected large-scale optical Ising machine with configurable two-body spin-spin interactions can be realized. Furthermore, by including a second-harmonic (SH) light generation through nonlinear crystal and measuring the superposition of the pump light and SH light intensities, we recently have realized a more general Ising model with both two-body and four-body spin interactions36. Our nonlinear optical Ising machine realizes a special class of the so-called k-local Hamiltonian which is useful for polynomial unconstrained binary optimization or high order binary optimization problems42,43.

A natural question that arises is whether such a nonlinear optical Ising machine can be used to solve optimization problems more efficiently. As the first step to address this important question, we experimentally and theoretically investigate the ground state magnetic phases of the nonlinear optical Ising machine for different four-body spin interaction coefficient and effective temperature. The ground state of the Ising model at different temperatures provides important information for the energy landscape. Understanding the ground state phase diagram can assist the search for the true ground state of the Ising model in the simulated annealing. Our main finding is that we can identify two distinct types of phase transitions with the order parameter—the magnetization—changes either continuously or abruptly to zero as the increase of temperature, corresponding to a second-order and a first-order phase transition respectively. We point out that similar Ising models with nearest-neighbor two-body and local four-body spin interactions have been theoretically explored in the 1970s44,45,46. To the best of our knowledge, our results represent the first experimental observation of two types of phase transitions in a configurable optical Ising model with fully connected two-body and four-body spin interactions.

Results

Experimental setup and Ising Hamiltonian

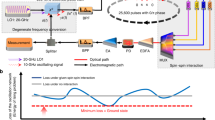
The schematic of the experimental setup for the nonlinear optical Ising machine is shown in Fig. 1a. We use a pump laser of wavelength λ ~ 1550.9nm incident on a SLM. A lens with focal length F = 200 mm is used to focus the light into a temperature-stabilized periodically poled lithium niobate (PPLN) crystal. It generates a SH light at λh ~ 775.5 nm. After passing through another lens, the pump and SH lights are separated by a dichroic mirror (DM), then coupled into the single mode fibers and detected by two separate power meters. The measurements are sent to the recurrent feedback, which updates the spins on the SLM according to the Monte Carlo Metropolis-Hastings algorithm to find the ground state of the given Ising problem36.

Fig. 1: Realization of a nonlinear optical Ising machine with two-body and four-body spin interactions.
figure 1

a Sketch of the experimental setup for the nonlinear optical Ising machine. The linearly polarized pump light (blue) incidents on a SLM, and then it is focused into a nonlinear crystal. The generated SH (red) and residual pump lights are coupled into separate single mode fibers and measured by the power meters. PBS: Polarizing Beam Splitter, HWP: Half Wave Plate, SLM: Spatial Light Modulator, PPLN: Periodically Poled Lithium Niobate, DM: Dichroic Mirror. b The two-body and (c) the reduced four-body spin interaction matrices Jij and Qij for a 20 × 20 spin system.

Full size image

The Hamiltonian of our Ising spin model is defined as the superposition of the pump and SH light intensities (see Methods),

$$H=-\mathop{\sum}\limits_{i,j}{J}_{ij}{\sigma }_{i}{\sigma }_{j}-\gamma \mathop{\sum}\limits_{i,j,s,r}{K}_{ijsr}{\sigma }_{i}{\sigma }_{j}{\sigma }_{s}{\sigma }_{r},$$
(1)

where we have multiplied − 1 for pump light intensity (so that a ferromagnetic phase is favored at T = 0) and γ is a tunable parameter. The two terms correspond to a two-body and a four-body spin interaction, with the following explicit expressions for the spin interactions

$${J}_{ij}=2\pi {\big({w}_{f}^{p}\big)}^{2}\frac{{a}^{4}}{{f}^{2}{\lambda }^{2}}{\xi }_{i}{\xi }_{j}{\xi }_{i}^{f}{\xi }_{j}^{f},$$
(2)
$${K}_{ijsr}=\frac{1}{2}\pi {A}_{s}^{2}{\big({w}_{f}^{h}\big)}^{2}\frac{{a}^{8}}{{F}^{2}{f}^{2}{\lambda }^{4}}{\xi }_{i}{\xi }_{j}{\xi }_{s}{\xi }_{r}{\xi }_{ij}^{{\prime} f}{\xi }_{sr}^{{\prime} f},$$
(3)

where \({\xi }_{i}^{f}=\exp [-\frac{{\pi }^{2}{({w}_{f}^{p})}^{2}}{{f}^{2}{\lambda }^{2}}({x}_{i}^{2}+{y}_{i}^{2})]\) and \({\xi }_{ij}^{{\prime} f}=\exp [-\frac{{\pi }^{2}{({\omega }_{f}^{h})}^{2}}{{f}^{2}{\lambda }^{2}}[{({x}_{i}+{x}_{j})}^{2}+{(\,{y}_{i}+{y}_{j})}^{2}]]\). It is worth pointing out that in the pump non-diffraction and non-depletion regime, the two-body and four-body spin interactions are not full-rank matrices. They can be decomposed as Jij = PiPj with \({P}_{i}=\sqrt{2\pi }{w}_{f}^{p}{a}^{2}{\xi }_{i}{\xi }_{i}^{f}/f\lambda\) and Kijsr = QijQsr with \({Q}_{ij}=\sqrt{\pi }{A}_{s}{w}_{f}^{h}{a}^{4}{\xi }_{i}{\xi }_{j}{\xi }_{ij}^{f}/\sqrt{2}Ff{\lambda }^{2}\). Thus, the two-body spin interaction Jij is a matrix of rank one and the reduced four-body interaction Qij is a matrix of rank N as the fiber mixes the light from different pixels (see Fig. 1b, c). Such low-rank two-body and four-body spin interactions may impose some limitations to the SLM-based optical Ising machine for solving complex optimization problems. This can be circumvented, for example, by adding a scattering medium in front of the detector, as proposed in the recent work38,47. Alternatively, the relative locations of the Fourier lenses can be changed to induce non-negligible diffraction inside the crystal48, or the pump power can be increased to enter the pump-depletion regime. In either case, Jij and Kijsr will become full rank matrices and the above decomposition is not valid anymore. Furthermore, the ratio between the four-body and two-body spin interactions can also be tuned by changing other parameters, such as the pixel length a, the laser’s beam width, etc., which may provide some additional flexibility for solving optimization problems with the nonlinear optical Ising machine.

Experimental results and numerical simulations

Our main experimental observations are summarized in Fig. 2a–c. For a fixed effective temperature T, the Ising energy decreases to its lowest value after some Monte-Carlo iterations and the corresponding magnetization increases from zero (as we start with an initial random spin configuration) to a finite value that depends on the four-body coefficient. As shown in Fig. 2c, the magnetization changes to zero continuously as a function of temperature for γ = 0, 100 while it drops to zero abruptly for γ = 500, indicating two different types of phase transitions. These experimental observations can be reproduced with a full Monte-Carlo numerical simulation. Using the same Metropolis-Hasting algorithm49, we randomly choose one spin each time to flip in order to reduce the total energy. The spin flip is accepted with the Boltzmann probability, similar to that adopted in the experiment. This allows the system to evolve out of energy local minima and have more chance to reach the ground state. As shown in Fig. 2d, the numerical results are qualitatively the same as the experimental results. One of the mechanisms for the discrepancy is related to the optical loss, which is not captured in our theoretical model. We further have performed another measurement with slightly different experimental parameters, such as higher pump power and better SH coupling into the fiber. Figure 3 shows the experimental results for the measured magnetization as a function of temperature for four different γ values. The pump power for the new measurement is about 1.3 times larger and thus the SH power is about 1.7 times larger compare to Fig. 2c. According to the Hamiltonian Eq. (1), the critical γ separating the second-order and the first-order phase transitions will be about 1.3 times smaller compared to that in the previous measurement of Fig. 2c, in consistent with the results presented in Fig. 3. By scanning the four-body coefficient γ and effective temperature T, we numerically obtain the phase diagram as shown in Fig. 4a. The phase diagram indicates that there is a second-order phase transition for small γ and a first-order phase transition for large positive γ. We further assume a uniform two-body and four-body spin interaction constants and obtain a qualitatively similar phase diagram shown in Fig. 4b.

Fig. 2: Ground state energy and magnetization of the nonlinear optical Ising machine.
figure 2

a Experimentally measured Ising energy and (b) magnetization of the spin model as a function of the Monte-Carlo iterations for four-body coefficient γ = 1 (blue) and 500 (orange). The inset of panel (b) shows the converged spin configurations of the Ising model at the end of the time evolution, with the blue and yellow pixels corresponding to opposite spins. c Experimentally measured magnetization as a function of temperature for γ = 0, 100, 500. d The same results obtained from full Monte-Carlo numerical simulation. Error bars in each measurement are less than the size of the dots. Errors in the experiment could be arise due to the slight laser power fluctuations, temperature variation, and optical misalignment, etc. In (c, d), the magnetization drops to zero continuously at γ = 1 (blue), 100 (orange) and abruptly at γ = 500 (green) with the thick lines the guides to the eyes.

Full size image
Fig. 3: Ground state magnetization of the nonlinear optical Ising machine.
figure 3

Here, the experimental parameters are slightly off compared to the results shown in Fig. 2c. The magnetization drops to zero continuously at γ = 0 (blue), 50 (orange) and abruptly at γ = 100 (green), 500 (red) with the thick lines the guides to the eyes. Error bars are similar to Fig. 2c.

Full size image
Fig. 4: Ground state phase diagrams of the nonlinear optical Ising machine.
figure 4

a, b are the results obtained from the full Monte-Carlo numerical simulation with the actual nonuniform and approximated uniform spin-spin interactions, respectively, and (c) is the result obtained from the MF theory where the system exhibits a 1st-order and a 2nd-order PT (phase transitions) separated by the white dashed line. The color bars represent the magnitude of the magnetization ∣m∣. d The free energy at the points labeled in panel (c) [on the yellow arrows] as a function of magnetization at different temperature T and four-body coefficient γ. The circle and square symbols correspond to the true ground state. In b, c, we have used uniform two-body and four-body spin interactions with J ≈ 0.19μW, K ≈ 3.6 × 10−9μW.

Full size image

Mean-field theory

To understand the two types of phase transitions observed in the nonlinear optical Ising machine, we develop a mean-field (MF) theory where the two-body and four-body spin interaction constants are assumed to be uniform and the fluctuation of the spin magnetization is small. The MF approximation is reliable as the spin interaction in our model is long ranged. Writing σi = m + δσi with m ≡ 〈σi〉 and expanding the spin Hamiltonian50 to linear order in the fluctuations δσi, we find

$$H=(J{m}^{2}{N}^{2}+3\gamma K{m}^{4}{N}^{4})-{h}_{eff}\mathop{\sum}\limits_{i}{\sigma }_{i},$$
(4)

where heff = 2JmN + 4γKm3N3. The corresponding partition function \(Z={{{{{{{\rm{Tr}}}}}}}}({e}^{-H/T})\) is given by

$$Z={e}^{-(J{m}^{2}{N}^{2}+3\gamma K{m}^{4}{N}^{4})/T}{\left[2\cosh ({h}_{eff}/T)\right]}^{N}.$$
(5)

The free energy of the spin system can be obtained with \(F\equiv U-TS=-T\ln Z\), where U is the thermal energy and S is the entropy of the system. Substituting the expression for the partition function into the free energy, we find

$$F=-NT\ln 2+J{m}^{2}{N}^{2}+3\gamma K{m}^{4}{N}^{4}-NT\ln \big[\cosh \big({h}_{eff}/T\big)\big].$$
(6)

The magnetization m can be calculated after a thermal average \(m={N}^{-1}{\sum }_{i}\langle {\sigma }_{i}\rangle ={N}^{-1}{\sum }_{i}{{{{{{{\rm{Tr}}}}}}}}({\sigma }_{i}{e}^{-H/T})/Z\) or by taking dF/dm = 0. A straightforward calculation gives the following self-consistent equation for the magnetization:

$$m=\tanh [(2JmN+4\gamma K{m}^{3}{N}^{3})/T].$$
(7)

Solving this equation and taking the solution that minimizes the free energy of the spin model yields the ground state magnetization. The MF phase diagram is shown in Fig. 4c which is consistent with that obtained from the Monte-Carlo simulation in the presence of a uniform spin-spin interaction (Fig. 4b).

We can gain some useful insight into the physics of this system by performing a Taylor expansion of the free energy (Eq. (6)) around m = 0:

$$F= -NT\ln 2+{N}^{2}J\left(1-\frac{2NJ}{T}\right){m}^{2}\\ +{N}^{4}\left[\frac{4N{J}^{4}}{3{T}^{3}}-\gamma K\left(\frac{8NJ}{T}-3\right)\right]{m}^{4}+{{{{{{{\mathcal{O}}}}}}}}({m}^{6}).$$
(8)

For γ = 0, the coefficient of the quartic term is always positive. According to Landau’s theory of phase transition51, only second-order phase transition is possible unless there are odd terms of magnetization appearing in the free energy expansion (such symmetry-breaking term, for example, can be induced by an external magnetic field). The system exhibits a second-order phase transition when the temperature is larger than a critical value, which can be analytically obtained by letting the coefficient of the quadratic term equal to zero. Hence, we find Tc = 2NJ.

For γ > 0, due to the interplay of the four-body and two-body spin interactions, the quartic term could be positive or negative, giving rise to much richer phase transition phenomena. Specifically, the second-order phase transition persists for smaller positive values of γ as the coefficient of the quartic term remains positive at T ≈ Tc. The phase transition behavior changes dramatically for large enough positive value of γ since the coefficient of the quartic term changes sign. By letting it equal to zero at T = Tc, we find a critical value of the four-body coefficient γc = J/(6N2K). Using the parameters for Fig. 4c, we find γc ≈ 55 which is very close to the exact numerical value. The discrepancy is due to the ignorance of higher-order terms in the expansion, which is required in order to obtain an accurate estimation of γc. As shown in Fig. 4d, the free energy function behaves distinctly at different four-body coefficients. For γ > γc, a local minimum at m = 0 appears in the free energy and the system exhibits a first-order phase transition if this new minimum at m = 0 becomes a global minimum at a higher temperature. The phase boundary between the ferromagnetic order and paramagnetic order for γ > γc can be estimated using the condition F(m = 0) = F(m = 1), which gives the simplified form \(\gamma =T(\ln 2)/(K{N}^{3})-J/(K{N}^{2})\). Therefore, the critical temperature for the first-order phase transition increases linearly as a function of the four-body coefficient. All these analytical results qualitatively agree with our phase diagram obtained by numerically solving the self-consistent equation, see Fig. 4c.

For γ < 0, our system also exhibits a second-order phase transition. However, as shown in Fig. 4c, the magnetization in the ferromagnetic phase decreases as γ changes from 0 to − 500 in order to suppress the four-body spin interaction energy.

Nonuniform spin interaction induced spatially structured magnetic phase

For γ < 0, our experimental observation (Fig. 5a) and Monte-Carlo numerical simulation (Fig. 5b) indicate that there is a spatially structured magnetic phase appearing: the inner part of the SLM exhibits a ferromagnetic phase with all the spins pointing to the same direction and the outer part of the SLM exhibits a long-range anti-ferromagnetic (AF) phase with these spins located at the opposite corners of the SLM pointing to opposite directions (see Fig. 5). This can be understood with the profile of the reduced four-body spin interaction matrix Qij (Fig. 1c) which depends on the matrix \({\xi }_{ij}^{{\prime} f}\) whose expression is given below in Eq. (3). The latter matrix has larger elements if ri + rj ≈ 0. To reduce magnetization, the spins located at the opposite side of the SLM favor opposite directions and the spins next to each other favor the same direction in order to reduce the four-body interaction energy. On the other hand, at the inner part of the SLM where the light intensity is stronger, the two-body interaction dominates and thus a ferromagnetic phase with all the spins point to the same direction is preferred. Consequently, a domain wall that separates the two regions of opposite spins is formed on the SLM (see the inset of Fig. 5a, b).

Fig. 5: Zero temperature magnetic phases of the nonlinear optical Ising machine with a negative four-body coefficient γ < 0.
figure 5

a Experimentally measured and (b) numerically obtained magnetization as a function of γ. The error bars in (a) are close to the size of the dots. The magnetization saturates to a nonzero value for large ∣γ∣. The inset figures are the spin configurations for some selected γ values. The spins located at the opposite corners of the SLM are antiparallel with each other, giving rise to an anti-ferromagnetic (AF) order shown by red arrow.

Full size image

Conclusion

In summary, we have performed systematic investigations of the magnetic phases of the nonlinear optical Ising machine. The exhibited rich phase diagram is a direct consequence of the competition between two-body and four-body spin interactions at different effective temperature. The great flexibility of the nonlinear optical Ising machine may be useful for solving optimization problems where the four-body spin interaction coefficient can be gradually tuned for simulated annealing in order to quickly find the optimal solution52,53,54,55. Our system can be further generalized by considering an anti-ferromagnetic or random two-body spin interactions and including other higher-order spin interactions through sum frequency generation, four-wave mixing, and high harmonic generations. It can be used for the study of q-state Potts model56,57 and the development of self-learning Monte-Carlo algorithm58, etc.

Methods

Design of nonlinear optical Ising machine

We use a mode-locked laser of wavelength λ ~ 1550.9 nm with an average power of 70mW as the pump light. The full width half maximum of the pump beam is wp = 3.8 mm which is incident on the SLM (Santec SLM-100, 1440 × 1050 pixels, pixel length a = 10μm). The region of interest on the SLM is defined as a square lattice of N = 20 × 20 giant spins with each spin consisting of 20 × 20 pixels of the same phase which is modulated to be 0 or π to generate a random initial spin configuration. The unmodulated portion of the pump light is deflected by an optimized blazed grating. A lens with focal length F = 200 mm is used to focus the modulated beam into a temperature-stabilized periodically poled lithium niobate (PPLN) crystal with a poling period of Λ = 19.36 μm (5mol.% MgO-doped PPLN, length 1cm from HC Photonics). It generates a SH light at λh ~ 775.5 nm59. After passing through another lens of the same focal length, the pump and SH lights are separated by a dichroic mirror (DM) and then coupled into the single mode fibers (SMF-28) using fiber collimators with aspheric lenses Thorlabs C220TMD-C and A375TM-B, respectively, and detected by the power meters (Thorlabs PM-100D with sensors S132C and S130C). The measurements are sent to the computer MATLAB interface, which completes the feedback loop by updating the SLM36. The spin flipping during each iteration is accepted or rejected according to a Boltzmann probability function \(P=\exp (-{{\Delta }}U/T)\), where ΔU = Enew − Eold is the change in energy of a target Hamiltonian and T is the effective temperature (see Fig. 1a).

Theoretical Model

Since the phase of the light incident on the SLM is modulated to be either 0 or π, we can model the electric field of the incident light with the following discretized form

$${E}_{p}({{{{{{{\bf{x}}}}}}}})=\mathop{\sum}\limits_{i}{\xi }_{i}{\sigma }_{i}{{{{{{{\rm{rect}}}}}}}}\left(\frac{{{{{{{{\bf{x}}}}}}}}-{{{{{{{{\bf{x}}}}}}}}}_{i}}{a}\right),$$
(9)

where x = (x, y) denotes the spatial coordinate on the SLM plane, xi is the position of the ith pixel, a is the pixel length, σi = ± 1 is the phase of the pump light, and \({\xi }_{i}={E}_{0}{e}^{-({x}_{i}^{2}+{y}_{i}^{2})/{w}_{p}^{2}}\) corresponds to the amplitude of the Gaussian beam, rect(x) = rect(x)rect(y) = 1 for ∣x∣ < 0.5 and ∣y∣ < 0.5 is the rectangular function. The wave reflected by the SLM passes through a lens of focal length F. On the focal plane, the wave is transformed to the Fourier domain according to

$${\tilde{E}}_{p}({{{{{{{{\bf{x}}}}}}}}}^{{\prime} })=\frac{1}{F\lambda }\int{E}_{p}({{{{{{{\bf{x}}}}}}}}){e}^{i\frac{2\pi }{F\lambda }{{{{{{{\bf{x}}}}}}}}\cdot {{{{{{{{\bf{x}}}}}}}}}^{{\prime} }}d{{{{{{{\bf{x}}}}}}}},$$
(10)

where \({{{{{{{{\bf{x}}}}}}}}}^{{\prime} }=({x}^{{\prime} },{y}^{{\prime} })\) denotes the spatial coordinate on the focal plane. A straightforward calculation gives

$${\tilde{E}}_{p}({{{{{{{{\bf{x}}}}}}}}}^{{\prime} })=\frac{{a}^{2}}{F\lambda }\mathop{\sum}\limits_{i}{\xi }_{i}{\sigma }_{i}{e}^{-i\frac{2\pi }{F\lambda }{{{{{{{\bf{x}}}}}}}}\cdot {{{{{{{{\bf{x}}}}}}}}}_{i}^{{\prime} }}{{{{{{{\rm{sinc}}}}}}}}\left(\frac{\pi a{{{{{{{\bf{x}}}}}}}}}{F\lambda }\right),$$
(11)

where \({{{{{{{\rm{sinc}}}}}}}}({{{{{{{\bf{x}}}}}}}})=\sin (\pi x)\sin (\pi y)/(xy)\) denotes the two-dimensional sinc function.

The PPLN nonlinear crystal placed at the focal point of the lens generates SH light of frequency ωh. In the pump non-diffraction and non-depletion regime60, the pump light in the nonlinear crystal does not change while the SH light can be obtained as \({\tilde{E}}_{h}({{{{{{{{\bf{x}}}}}}}}}^{{\prime} })={A}_{s}{\tilde{E}}_{p}^{2}({{{{{{{{\bf{x}}}}}}}}}^{{\prime} })\) where \({A}_{s}=i{\omega }_{h}^{2}{\chi }^{(2)}L/(2{\kappa }_{h}{c}^{2})\), L is the length of the nonlinear crystal, χ(2) is the second-order susceptibility, c is the speed of light, κh = 2πnh/λh is the wave number of the SH light, and nh is the index of refraction. After passing through two lenses of focal length F and f, the pump light and SH light are subsequently coupled into the fibers and then the intensities are measured. The light intensity coupled into the fiber can be defined as \(P=\frac{1}{2}c{\epsilon }_{0}| \int\,E({{{{{{{\bf{u}}}}}}}}){E}_{f}({{{{{{{\bf{u}}}}}}}})d{{{{{{{\bf{u}}}}}}}}{| }^{2}\), where u = (u, v) and \({E}_{f}({{{{{{{\bf{u}}}}}}}})=\sqrt{\frac{2}{\pi }}\frac{1}{{w}_{f}}\exp (-\frac{{u}^{2}+{v}^{2}}{{w}_{f}^{2}})\) are the spatial coordinate and lowest optical mode (characterized by the width wf which is slightly different for the pump and SH lights) of the fiber, respectively. The Hamiltonian of our Ising spin model is defined as the superposition of the pump and SH light intensities (see Eq. (1)).