Introduction

Cells from all kingdoms of life use pH gradients to drive the synthesis of ATP via ATP synthase1. This is often seen as an indication that pH gradients were also a driving force during the emergence of life. This hypothesis is substantiated by phylogenetic analysis2 and geochemical considerations3,4. In non-equilibrium settings, such as heat flows through rock fissures or hydrothermal systems, pH gradients can provide a prebiotic proton-motive force to drive early metabolisms5. Prebiotic systems may also benefit from pH gradients to localize pH-selective chemical reactions such as nucleotide adsorption6 to certain spatial zones, or to spatially couple the effects of ribozymes that operate at different pH7. However, the physicochemical mechanisms that can produce pH gradients in plausible non-equilibrium settings are so far insufficiently understood.

Experimentally, a controlled non-equilibrium setting to study the formation of chemical gradients is created by heat flows across microfluidic chambers8,9. Such experiments mimic ubiquitous natural settings, e.g. in porous rocks near hydrothermal vents10 (Fig. 1b). A previous study demonstrated that heat flow across narrow (100 μm-scale) pores can induce pH gradients of 2 units along the pore length (mm-scale)11. The gradients were generated by a complex interplay of convection, thermophoresis, electrostatic interactions, and acid-base reactions.

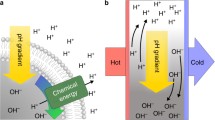
Fig. 1: Heat flows create pH gradients in acid-base mixtures.
figure 1

a Dominant dynamic processes in a heat flux chamber: Chemical reactions (gray) remain locally equilibrated (τchem ≲ 10−3 s). Thermophoretic horizontal accumulation (τphor ~ 102 s, orange arrows) is faster than vertical Rayleigh-Bénard convection (τconv ~ 104 s, green arrows), given the high aspect ratio (height/width) of the heat flux chamber that mimics, e.g., a rock fissure. Thermophoresis and convection combined drive a selective accumulation of molecules. Their net accumulation is proportional to their effective Soret coefficient \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\), derived in the main text. b Heat flows across rock fissures provide a non-equilibrium environment that drives proton gradients. By analyzing local outflows with standard pH-meters, we measure the pH values quasi in situ. c By tuning the concentrations of acids and bases, both amplitude and direction of the created pH gradient can be controlled.

Full size image

Here, we focus on the physical parameters of this interplay to understand the control of both the amplitude and the direction of the pH gradient (Fig. 1c). We performed an experimental case study (Fig. 1a) of a prebiotically relevant12,13 acid-base system consisting of formic acid (HCOOH) and sodium hydroxide (NaOH) diluted in an aqueous solution. The mixture was kept within a microfluidic chamber and subjected to a lateral heat flow. Based on a separation of timescales, we then developed a heuristic theoretical description for this reaction-transport system, which incorporates the electrostatic coupling between the reacting species, as well as their transport due to drift and diffusion processes. This description captures the parameter dependence of the experimentally observed behavior, including a concentration-dependent steepening and inversion of the pH gradient. The model can be generalized to systems with more reacting species subject to electrostatic coupling, as long as the effective timescales of the local reactions and the global transport are sufficiently separated. The quantitative understanding enables the prediction and the control of thermally induced pH gradients.

Results

Experimental setup and procedure

For this study, we developed a continuous flow microfluidic device with openings that allowed us to probe the local pH at three different outflow positions and using standard pH meters (Fig. 2a; see Methods for a detailed description). This setup avoids complications imposed by a fluorescent pH reporter needed to monitor pH in a closed device11.

Fig. 2: Experimental setup and results.
figure 2

a Experimental setup. The thin thermal reaction chamber is continuously supplied with a premixed solution containing varying concentrations of formic acid and sodium hydroxide. The outflux is split into three parts (top 12%, middle 76% and bottom 12%) and the pH value of each fraction is measured (green circles). For experimental details see Methods. b These pH values are depicted for 75 mM formic acid and varying concentrations of NaOH (mNa) for the inlet (bulk) and the different outlets. While the bottom fraction qualitatively follows the bulk, especially the top fraction displays a complex, concentration-dependent behavior both for its value and for the resulting pH gradient \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{vert}}}}}}}}}\) between top and bottom of the heat flux cell (measurements for other formic acid concentrations shown in Supplementary Fig. 2). c When plotting the pH values of the different fractions (black circle: bulk, brown inverted triangle: top, green box: middle, pink triangle: bottom), a positive gradient (pHtop > pHbot, red) for low concentrations of NaOH is observed which is inverted (blue) at higher concentrations of NaOH and increases massively when mNa > mHCOOH. Error bars are shown as discussed in Methods. d In the absence of a temperature gradient, no pH gradient forms (mHCOOH = 75 mM).

Full size image

The microfluidic structure containing the fluid was cut out of fluorinated ethylene propylene (FEP) foil and subsequently sandwiched between two sapphire windows (chamber dimensions: width w = 170 μm, height h = 50 mm). This design guaranteed that the liquid sample only has contact to FEP and sapphire, providing an inert environment even for aggressive chemistry. Sapphire was chosen for its transparency (for optical control) and high heat conductivity (to ensure a homogeneous temperature distribution). One of the sapphire windows was cooled by an aluminum heat exchanger connected to a cryostat, while the other window was kept at high temperatures by Ohmic heating, resulting in a constant heat flux through the chamber. The device had one inlet at the left side and three outlets at the right side, at different vertical positions (‘top’, ‘middle, ‘bottom’) where the pH value was measured.

The inlet was used to push a mixture of pure water, acid and base (with initial pH value denoted as pH0) at a flow rate of 3.28 nl/s into the chamber. Using syringe pumps at each of the outlets, the flux splitting between the three outlets was adjusted to outflow fractions of 12% (top), 76% (middle), and 12% (bottom). These values reflect a trade-off that kept the thermogravitational accumulation within the chamber relatively unperturbed, the total time required for the experiment manageable and the spatial regions from which the top and bottom samples are collected relatively localized (see Methods for a detailed discussion).

Experimental pH gradients

Using this setup, we performed experiments with solutions containing different amounts of formic acid (mform) and NaOH (mNa). The heat flow through the chamber was set by keeping the temperatures at the front and back at 60 ± 2 ∘C and 21 ± 1 ∘C, respectively. The pH values of the different fractions obtained with 75 mM formic acid and varying amounts of NaOH are shown in Fig. 2b, c (for other formic acid concentrations see Supplementary Fig. 2).

While the pH in the bottom of the cell qualitatively follows the pH behavior in the equilibrated bulk solution (see Supplementary Fig. 1), the pH in the middle and top fractions displays a markedly different behavior as a function of the NaOH concentration. The pH dependence in the bottom fraction of the cell and the bulk solution is consistent with well-known acid-base characteristics, with a change from acidic to alkaline at equimolar concentrations of NaOH and formic acid. However, the pH behavior in the top fraction is surprisingly complex, leading to a previously not observed11 inversion of the pH difference \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{vert}}}}}}}}}\) (see Fig. 3) between the top and bottom fraction at low NaOH concentrations ( ~ 10 mM). Above equimolarity, the pH difference sharply increases. Despite NaOH being a strong base, even at NaOH concentrations much larger than formic acid concentrations, the pH value of the top fraction is actively pushed into the acidic regime by the heat flux.

Fig. 3: Comparison of analytically predicted and experimentally measured pH gradients.
figure 3

a Heat maps of theoretically calculated pH differences are compared to measurements (circles) for varying concentrations of formic acid (mform) and sodium hydroxide (NaOH, mNa). Our model predicts a complex phase diagram with a positive (yellow), a weakly negative (green) and a strongly negative (blue) pH gradient. The inversion is shown by a black dashed line and corresponds to \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}=0\), see Eq. (9). The experimental results are in very good agreement with the analytical model. b Theoretical (orange line) and experimental (blue circles) pH differences for 150 mM and 75 mM formic acid (white lines in a), showing again the good agreement between theory and experiment. The error bars include experimental standard deviations from replicate measurements as well as uncertainties accounting for concentration fluctuations from thermal gradient effects in the outflow channels (for more details see Methods).

Full size image

Theoretical approach

The complex experimental behavior of the emergent pH gradient arises from the combined effects of diffusion, convection, thermophoresis, electrostatic interactions, and acid-base reactions. The interplay of these effects can be studied by numerically solving the underlying reaction-transport equations, but a full characterization of the system is challenging, due to the large parameter space and the multiple different timescales of the dynamics11.

Due to thermal expansion of the solvent and gravity acting in vertical direction, an approximately rotationally symmetric circular buoyant convection flow is established in the chamber: solutes closer to the hot side will be driven upwards while molecules on the cold side will be transported downwards. Additionally, dissolved molecules are driven along the horizontal temperature gradient by thermophoresis. While the magnitude of the ensuing velocities of both processes are comparable, a small aspect ratio w/h causes the horizontal equilibration to occur on a faster timescale than the vertical accumulation, see Fig. 1a and Methods. Seminal work by P. Debye showed that an expansion in the aspect ratio yields approximate solutions, where concentration gradients along the horizontal dimension shape those along the vertical dimension of the setup14. Electrostatic interactions were taken into account for electrolytes by Guthrie and coworkers15. From a theoretical perspective, the task at hand therefore is to explicitly integrate chemical reactions to the theoretical description, and to study their effect on the system behavior. Until now, only the case of a chemical reaction of a single species without electrostatic interactions has been considered16.

In this work, we derive an expression for vertical concentrations gradients, in particular, the proton gradient, as a function of the initial chemical concentrations. In the following, we will rely on a timescale separation between the (zero-dimensional) chemical reaction dynamics, the (one-dimensional, horizontal x-axis) effects of thermophoresis and the (two-dimensional, x–y axis) effects of buoyant convection, see Fig. 1.

Chemical dynamics

Our system is determined by the system of the \({{{{{{{\mathcal{R}}}}}}}}=3\) chemical reactions

$${{{{{{{\rm{HCOOH}}}}}}}}\quad \mathop{\rightleftharpoons }\limits^{{K}_{a}}\quad {{{{{{{{\rm{COOH}}}}}}}}}^{-}+{{{{{{{{\rm{H}}}}}}}}}^{+},$$
(1)
$${{{{{{{{\rm{H}}}}}}}}}_{2}{{{{{{{\rm{O}}}}}}}}\quad \mathop{\rightleftharpoons }\limits^{{K}_{w}}\quad {{{{{{{{\rm{OH}}}}}}}}}^{-}+{{{{{{{{\rm{H}}}}}}}}}^{+},$$
(2)
$${{{{{{{\rm{NaOH}}}}}}}}\quad \mathop{\rightleftharpoons }\limits^{{K}_{b}}\quad {{{{{{{{\rm{Na}}}}}}}}}^{+}+{{{{{{{{\rm{OH}}}}}}}}}^{-},$$
(3)

where we assume that the concentration of H2O is approximately constant. The equilibrium concentrations \({c}_{i}^{0}\) of the \({{{{{{{\mathcal{N}}}}}}}}=6\) dynamical chemical species Xi are determined by the equilibrium constants for the acid, base, and water, respectively:

$$\begin{array}{c}{K}_{a}=\frac{{c}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}^{0}{c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}^{0}}{{c}_{{{{{{{{\rm{HCOOH}}}}}}}}}^{0}},\quad {K}_{b}=\frac{{c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}^{0}{c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}^{0}}{{c}_{{{{{{{{\rm{NaOH}}}}}}}}}^{0}},\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!{K}_{w}={c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}^{0}{c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}^{0}.\end{array}$$
(4)

In general, closed chemical systems always conserve certain chemical sub-species, so-called moieties17. We define the moiety concentrations

$${m}_{{{{{{{{\rm{form}}}}}}}}} =\, {c}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}+{c}_{{{{{{{{\rm{HCOOH}}}}}}}}},\quad {m}_{{{{{{{{\rm{Na}}}}}}}}}={c}_{{{{{{{{\rm{NaOH}}}}}}}}}+{c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}},\\ {m}_{{{{{{{{\rm{c}}}}}}}}} =\, {c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}+{c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}-{c}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}-{c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}.$$
(5)

Here, mform and mNa are the total concentration of formate and sodium-containing molecules in the system, which are experimentally controllable parameters. Similarly, mc is the net charge concentration. Notice that the moieties are not uniquely defined, and any linear combination of a moiety yields another conserved quantity. However, we can always define them in a way that includes the charge moeity and experimentally controllable parameters. Specifying the moiety concentrations mNa and mform and using, due to charge neutrality, mc = 0, together with Eqs. (4) uniquely determines the values of the equilibrium concentrations \({c}_{i}^{0}\) of all chemical species. Even though the full system is not at equilibrium, given that chemical reactions occur on the fastest timescale τchem < 10−3 s, the relations between the homogeneous equilibrium concentrations Eqs. (4), will hold approximately as local relations also in a spatially extended system.

Horizontal currents

Next, we consider the horizontal currents that form due to thermophoresis in an effective one-dimensional system. This is motivated since the timescale of the horizontal dynamics is given by τphor ≫ τchem (see Methods). The horizontal flux Ji(x) of molecule species Xi with horizontal concentration profile ci(x) is given by

$${J}_{i}=-{D}_{i}\frac{\partial {c}_{i}}{\partial x}-\left({S}_{i}{D}_{i}\frac{\partial T}{\partial x}-{z}_{i}{D}_{i}\frac{FE}{RT}\right){c}_{i},$$
(6)

where Di, Si, and zi are the diffusion constant, Soret coefficient, and valence of Xi, T(x) is a linear temperature profile, F the Faraday constant, and E the electrical field. In a steady state, the divergence of these currents is balanced by a source term given by the chemical reactions. Due to moiety conservation in local chemical reactions, the associated moiety currents are divergence-free. Since in a one-dimensional closed system any divergence-free current must vanish, it follows that the (horizontal) moiety currents I vanish identically. The vanishing electric current, \({I}_{{{{{{{{\rm{c}}}}}}}}}={J}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}+{J}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}-{J}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}-{J}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}=0\), allows us to solve for the electrical field

$$\frac{FE}{RT}=\frac{{\sum }_{i}{z}_{i}{D}_{i}\left(\frac{\partial {c}_{i}}{\partial x}+{S}_{i}{c}_{i}\frac{\partial T}{\partial x}\right)}{{\sum }_{i}{z}_{i}^{2}{c}_{i}{D}_{i}}.$$
(7)

Inserting this expression into (6) allows us to express the currents \({{{{{{{\boldsymbol{J}}}}}}}}=\left({J}_{{{{{{{{\rm{H}}}}}}}}},{J}_{{{{{{{{\rm{OH}}}}}}}}},{J}_{{{{{{{{\rm{HCOOH}}}}}}}}},{J}_{{{{{{{{\rm{COOH}}}}}}}}},{J}_{{{{{{{{\rm{Na}}}}}}}}},{J}_{{{{{{{{\rm{NaOH}}}}}}}}}\right)\) as linear functions of the horizontal concentration gradients \({{{{{{{{\boldsymbol{\partial }}}}}}}}}_{x}{{{{{{{\boldsymbol{c}}}}}}}}=\left(\frac{\partial {c}_{{{{{{{{\rm{H}}}}}}}}}}{\partial x},\frac{\partial {c}_{{{{{{{{\rm{OH}}}}}}}}}}{\partial x},\frac{\partial {c}_{{{{{{{{\rm{HCOOH}}}}}}}}}}{\partial x},\frac{\partial {c}_{{{{{{{{\rm{COOH}}}}}}}}}}{\partial x},\frac{\partial {c}_{{{{{{{{\rm{Na}}}}}}}}}}{\partial x},\frac{\partial {c}_{{{{{{{{\rm{NaOH}}}}}}}}}}{\partial x}\right)\) as J = D∂xc + b. The matrix D is a (cross-)diffusion matrix with components \({{{{{{{{\bf{D}}}}}}}}}_{ij}={\delta }_{ij}{D}_{i}+{D}_{j}{z}_{j}{c}_{j}\frac{{z}_{i}{D}_{i}}{{\sum }_{k}{z}_{k}^{2}{c}_{k}{D}_{k}}\) and \({{{{{{{{\boldsymbol{b}}}}}}}}}_{j}=-{D}_{j}{c}_{j}\frac{\partial T}{\partial x}{S}_{j}^{{{{{{{{\rm{ES}}}}}}}}}\), where

$${S}_{j}^{{{{{{{{\rm{ES}}}}}}}}}={S}_{j}-{z}_{j}\frac{{\sum }_{k}{z}_{k}{D}_{k}{S}_{k}{c}_{k}}{{\sum }_{k}{z}_{k}^{2}{c}_{k}{D}_{k}}$$

is the Seebeck coefficient, see also refs. 15,18.

The remaining two horizontal moiety currents I = (INa, Iform) = LJ are given by a \(2\times {{{{{{{\mathcal{N}}}}}}}}\) matrix L as a linear combination of J. Similarly to the charge current Ic, they are divergence-free and thus vanish, and we can write I = 0 as a linear equation for the horizontal concentration gradients ∂xc

$$\left({{{{{{{\bf{L}}}}}}}}{{{{{{{\bf{D}}}}}}}}\right){{{{{{{{\boldsymbol{\partial }}}}}}}}}_{x}{{{{{{{\boldsymbol{c}}}}}}}}={{{{{{{\bf{L}}}}}}}}{{{{{{{\boldsymbol{b}}}}}}}}.$$
(8)

In order to uniquely solve for the concentration gradients, additional constraints are needed. One of these constraints is given by the condition of approximate local electroneutrality in the bulk, mc(x) = 0, ∀ x, which can be systematically derived19,20. Differentiating this condition with respect to the horizontal position yields ∑izi∂xci = 0, which we can write with a \(1\times {{{{{{{\mathcal{N}}}}}}}}\) matrix Z with entries zi as:

$${{{{{{{\bf{Z}}}}}}}}{{{{{{{{\boldsymbol{\partial }}}}}}}}}_{x}{{{{{{{\boldsymbol{c}}}}}}}}={{{{{{{\boldsymbol{0}}}}}}}}.$$
(9)

Finally, since chemical reactions are fast as compared to the transport processes, we can assume that their concentrations ci(x) obey Eqs. (4) as local equilibrium relations. Taking the horizontal derivatives yields

$${{{{{{{\bf{Q}}}}}}}}{{{{{{{{\boldsymbol{\partial }}}}}}}}}_{x}{{{{{{{\boldsymbol{c}}}}}}}}={{{{{{{\boldsymbol{0}}}}}}}},$$
(10)

where Q is the \(3\times {{{{{{{\mathcal{N}}}}}}}}\) (Jacobian) matrix of the mass-action ratios.

Equations (8), (9) and (10) constitute \({{{{{{{\mathcal{N}}}}}}}}=6\) linearly independent equations for the \({{{{{{{\mathcal{N}}}}}}}}=6\) concentrations gradients. They can be inverted with a computer algebra system to give the concentrations gradients ∂xc as non-linear and convoluted expressions of the concentrations. In particular, we obtain a solution for the proton gradient, which we can formally write as

$$\frac{\partial {c}_{{{{{{{{\rm{H}}}}}}}}}}{\partial x}=-{S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}[\{{c}_{i}(x)\}]\frac{\partial T}{\partial x}{c}_{{{{{{{{\rm{H}}}}}}}}}.$$
(11)

with the concentration-dependent effective Soret coefficient for the hydrogen ion \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}\), whose sign and magnitude determine the horizontal proton gradient (see also Supplementary Note 1 for a complete solution). We consequently expand \({c}_{i}(x)={c}_{i}^{0}+{\gamma }_{i}(x)\) around the (homogeneous) bulk equilibrium concentrations, i.e. \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}={S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}(\{{c}_{i}^{0}\})+{{{{{{{\mathcal{O}}}}}}}}(\{{\gamma }_{i}(x)\}).\) For small temperature gradients and small widths of the heat flux chamber, we assume \({\gamma }_{i}\ll {c}_{i}^{0}\) and neglect the inhomogeneous part. Since the \({c}_{i}^{0}\) are uniquely determined by the moieties, i.e. the controlled molar concentrations of sodium hydroxide, mNa, and formic acid, mform, the homogenous effective Soret coefficient \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}({m}_{{{{{{{{\rm{Na}}}}}}}}},{m}_{{{{{{{{\rm{form}}}}}}}}})\) can be calculated from tunable experimental conditions.

The scheme outlined above will work for arbitrary chemical reactions networks and is thus general. On first glance, it might be surprising that we obtain exactly \({{{{{{{\mathcal{N}}}}}}}}\) independent linear equations for the \({{{{{{{\mathcal{N}}}}}}}}\) gradients of dynamical species. However, this fact can be traced to the algebraic structure of the stoichiometric matrix17. In particular, situations can arise where not all of Eqs. (4) leading to Eq. (10) are independent. However, the number of independent equations defining the moeities, Eqs. (5), and thus Eqs. (8) are algebraically related, such that we can always find \({{{{{{{\mathcal{N}}}}}}}}\) linear equations for the gradients of \({{{{{{{\mathcal{N}}}}}}}}\) dynamical species, regardless of the number \({{{{{{{\mathcal{R}}}}}}}}\) of reactions involved (see Methods or ref. 17).

Vertical pH gradient

Integrating equation (11) along the horizontal axis yields a horizontal pH difference \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{hor}}}}}}}}}\approx \frac{\Delta T}{\ln (10)}{S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\). Given such horizontal gradients, a theory for calculating the resulting vertical concentration gradient in a Clusius column has been formulated by Debye14, and adapted later to a situation including electrical fields15. This approach works, since the corresponding convective timescale τconv is much larger than the thermophoretic timescale, τconv ≫ τphor (Methods). It then turns out that the relation between horizontal and vertical gradients is given by a linear factor αth = 358.5, whose value depends only on material parameters of the solution, the geometric aspect ratio of the chamber, and the applied temperature gradient (see Methods). As such, the effective Soret coefficient \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}\) for the horizontal dynamics can be used to estimate the vertical pH difference \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{vert}}}}}}}}}\) measured experimentally,

$${\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{vert}}}}}}}}}\approx\alpha_{{{{{\rm{th}}}}}}\cdot S_{{{{{\rm{H}}}}}}^{{{{{\rm{eff}}}}}, 0} ({m_{{{{{\rm{Na}}}}}}},{m}_{{{{{\rm{form}}}}}})$$
(12)

Hence, weaker and more plausible temperature gradients in nature can be balanced by equally more plausible larger aspect ratios. As consequence, there is no lower threshold of temperature difference required for the formation of proton gradients, since shallow gradients can be compensated with higher aspect ratio21.

Comparison with experiments

The heat map from our theoretical model can roughly be divided into three regions: positive (yellow), weakly negative (green) and strongly negative (blue). As depicted in Fig. 3a, our measurements (shown in circles) fully recapitulate this behavior, both for the amplitude of the pH gradient and its inversion.

To avoid distortion from the flow extraction for pH measurement, we chose a slow flow (τflow = 13,000 s). This timescale is the time that a volume element on average remains in the heat flux chamber before it is extracted horizontally by the measurement cross-flow (z-axis in Fig. 2a). The slow extraction can however also slightly change the mNa/mform ratio in the effluent channel by thermophoretic accumulation, for which we estimate a systematic error of 2%. This effect has the greatest impact in the vicinity of mNa = mform, since the local pH then depends sensitively on the concentration ratio. This is reflected in the large error in pH determination at mNa/mform = 1.1 in Fig. 3b (see Methods).

Discussion

The experimental measurements are in good agreement with our analytical results. The characteristic, concentration-dependent features of an early inversion and massive increase at equimolar concentrations are reproduced without fitting parameters. The used solutes, formic acid and sodium hydroxide, are an example of a prebiotically plausible acid-base reaction system22,23,24,25. Possible roles of formic acid in prebiotically relevant synthesis reactions have been investigated23,26,27,28 together with the link to formamide-based reactions29,30.

Our analytical approach provides a more generally applicable theory for the interplay of chemical reactions, electrostatic interactions, and transport processes driven by external gradients. In the present case of thermally driven pH gradients, it allows a deeper understanding, and, compared to the previous computational analysis by Keil et al.11, it permits the treatment of strong acids and bases and much steeper pH gradients. This theoretical advance is complemented by our experimental method to measure local pH values in the heat flux cell using standard pH meters. These can cover a far broader pH spectrum and strong acids/bases compared to fluorescence methods. Together, this enables us to control and predict proton gradients and opens the door to applications involving synthesis reactions and the formation of tunable chemical gradients.

While the local equilibrium assumption is an excellent approximation in the present experimental context, it would be desirable to relax this assumption, in order to be able to apply the presented theoretical framework also to systems with slower chemical reactions. The behavior of such systems depends explicitly on the Damköhler number, a parameter that measures the relative timescales associated with the transport and reaction kinetics31. The inverse Damköhler number may serve as a useful expansion parameter to systematically extend the presented theoretical framework.

An intuitive explanation of the sign change of the pH gradient can be given by using the Soret coefficients listed in Supplementary Table 1 and considering all prevalent electrostatically coupled species. For this, we take into account that ions (H+, OH−, COOH−, Na+) show much stronger thermophoresis than uncharged substances, which can thus be neglected in this qualitative discussion. Therefore, at vanishing concentrations of NaOH (mNa), the only relevant ion pair for thermophoresis is COOH− and H+. Its enrichment in the lower part of the chamber increases the proton concentration and correspondingly lowers the pH value. With higher NaOH concentrations, ion pairs such as Na+ and OH− become more dominant and by accumulation therefore also more prevalent at the chamber bottom. This results in an increasing local pH value, first compensating the accumulated protons, and finally inverting the pH gradient.

Along this line of reasoning, the respective influence of the contributions of thermophoresis, thermal convection, chemical reactions, and electrostatics can also be understood. While thermophoresis by itself is only a weak effect, it is exponentially amplified by thermal convection14. Neglecting electrostatic interaction in an ion-bearing system would lead to their accumulation according to their Soret coefficient (see Supplementary Table 1). Consequently, a less complex pH difference profile is achieved with higher pH differences at low concentrations of NaOH due to a larger proton transport that otherwise is counteracted by electrostatic forces (Supplementary Fig. 5c). The temperature dependence of the reaction rate constants has only a minor impact on the formation of the pH gradient and can therefore be neglected in the following considerations (see Supplementary Fig. 5b/c). In contrast, a system devoid of chemical reactions is dominated by thermogravitational accumulation. This leads to a well-defined concentration ratio of the solutes and accordingly to a constant pH difference between the upper and lower part of the chamber irrespective of the absolute NaOH concentration (see Supplementary Fig. 5a). In absence of a thermal gradient, no accumulation and no pH gradient occur (Fig. 2d). Therefore, only the consideration of all these effects together provides a comprehensive understanding of this highly coupled system.

Since heat fluxes are ubiquitous on Early Earth, requirements for proton gradients to occur are significantly less demanding than complex chemical non-equilibria e.g. originating from confluent outflows from reservoirs with different pH32. Cooperative coupling to other gradients such as ion gradients33 will show interesting effects and help to solve enigmas such as prebiotically required separation of long RNA strands. Recent work by Mariani et al. has evaluated strand separation minimizing hydrolysis by pH oscillations34. This effect was recently used in a system of air-water interfaces to boost the replication of DNA35.

Methods

Preparation of heat flow chambers and microfluidic setup

The FEP-foil (Holscot, Netherlands) with a thickness of 170 μm (width) is cut by an industrial plotter device (CE6000-40 Plus, Graphtec, Germany) and sandwiched between two sapphires (Kyburz, Switzerland) with a thickness of 500 μm (cooled sapphire) and 2000 µm (heated sapphire), respectively. The back sapphire has 4 laser-cut holes with a diameter of 1 mm. The sapphire-FEP-sapphire block is then placed on an aluminum base covered by a heat conducting foil (EYGS091203DP, Graphite, 25 μm, 1600 W/mK, Panasonic, Japan) and held in place by a steel frame, mounted by six torque-controlled steel screws for a homogeneous force distribution. A second heat conducting foil (EYGS0811ZLGH, Graphite, 200 μm, 400 W/mK, Panasonic, Japan) connects the heated sapphire with the electrical heater element, and is also fixed by torque-controlled steel screws. The height of the microfluidic chamber is measured using a confocal micrometer (CL-3000 series with CL-P015, Keyence, Japan) at three positions (top, mid, bottom) to ensure homogeneous width along the chamber. Chambers are pre-flushed using low-viscosity, fluorinated oil (Novec™ 7500 Engineered Fluid, 3M, USA) to check for tightness and push out residual gas inclusions. The assembled chamber is then mounted to a cooled aluminum block. The Ohmic heaters are connected to a 400 W, 24 V power supply that is controlled via Arduino boards with a customized version of the open-source firmware “Repetier”, originally made for 3D printing. All elements were optimized using finite-element simulation to provide a homogeneous temperature profile while minimizing the thickness of the sapphire windows and hence maximizing the thermal gradient.

The in- and outlets of the thermal chamber are connected via tubings to syringes placed on high-precision syringe pumps (Low Pressure Syringe Pump neMESYS 290N with Quadruple Syringe Holder Low-Pressure, cetoni, Germany). For the microfluidic connections, (all from techlab, Germany): connectors (Verbinder zöllig, UP P-702-01), end caps (Tefzel Cap for 1/4-28 Nut, UP P-755), screws (Nut, Delrin, flangeless, VBM 100.823-100.828), ferrules (Ferrule VBM 100.632) and tubings (Tubing Teflon (FEP), KAP 100.969) are used. The flow speeds of the syringe pumps (controlled via neMESYS UserInterface, cetoni, Germany) are chosen such that 12% of the inflow are sucked out at the top and at the bottom outlet, leaving 76% coming out of the middle outlet. The syringes used (all from Göhler-HPLC Syringes, Germany) are: Chemically Resistant Heavy Duty Syringes with PTFE seals: 2606814 and 2606035 (ILS, Germany).

Sample preparation and experimental procedure

The samples are prepared mixing formic acid (Carl Roth Gmbh, Germany) and sodium hydroxide (Sigma-Aldrich, USA) with MilliQ-water to reach the given concentration. The pH (for initial pH values as compared to theoretical predictions, see Supplementary Fig. 1) is measured using a Orion™ 9826BN Micro pH Electrode and a 8220BNWP Micro pH Electrode (both Thermo Fisher Scientific, USA), also used for pH measurements after the experiment. For strongly alkaline pH values ( >13), measurement is done using pH paper and a larger error was assumed.

The cryostat (TXF-200 R5, Grant, UK) is set to −30 ∘C and the heaters to 95 ∘C which results in a temperature difference from ~20 ∘C to 60 ∘C within the microfluidic chamber. Temperatures are measured on the sapphires with a heat imaging camera (ShotPRO Wärmebildkamera, EAN: 0859356006217, Seek Thermal, USA) and a temperature sensor (GTH 1170, Greisinger, Germany and B&B Thermo-Technik 06001301-10, Germany), giving an average cold temperatur of 21 ∘C ± 1 ∘C and an average hot temperature of 60 ∘C ± 2 ∘C. Averaging over the temperature differences throughout all experiments gives a value of 38.9 ∘C ± 1.4 ∘C (as the higher cold temperatures usually go together with higher warm temperatures). Before starting the experiment, the tubings and thermal chamber are re-flushed with fluorinated oil. The samples are then loaded into the inlet tubing. The experiment is started and left running for 6–7 days. To stop the experiment, the applied temperatures are set to room temperature. The samples are recovered from the tubings and collected for pH measurement.

Experimental uncertainties

The experimental error splits into two main contributions: one standard error from replicate measurements and one to account for concentration fluctuations caused by effects from the thermal gradient in the outflow channels. As described in the main text, our experimental setup was designed to determine the pH value as realistically as possible inside the heat flux cell. For this purpose, the pH values were measured with a standard laboratory pH meter and no pH-dependent dyes were used, which are not designed for use in these extreme temperature conditions and are not compatible with measurements in the entire pH range. However, since measurements using a pH meter are not possible directly inside the cell due to the small dimensions of the microfluidic system, we slowly and continuously extract the cell volume at the top, middle and bottom of the cell respectively to obtain the necessary measurement volume. By doing so and balancing the outflows with respect to each other, the cell volume is split into three fixed volume portions, of which the contents are extracted through the respective outlet. At the same time, we allow the appropriate amount of stock solution to flow through the input channel so that the cell is completely filled with fluid at all times.

The aim of these considerations was to keep the effects of this slow drift flow on the actual experiment as small as possible and thus to obtain an unbiased picture of the pH distribution inside the cell. The corresponding timescale τflow indicates how long a volume element introduced into the cell by the drift flow remains in the cell on average until extraction. If it is greater than the relaxation time of the accumulation process occurring in the heat flow cell, i.e. if the drift flow is sufficiently small, it can be assumed that the accumulation remains essentially undisturbed. If the drift flux is correspondingly too fast, the accumulation will be disturbed. For the extraction at the lower outlet, the following problem appears: In order to avoid a diffusive loss of accumulated material, we placed the exit hole for the lower output channel not at the bottom of the cell but rather sufficiently high (as shown in the main text, Fig. 2). However, this requires the to-be extracted material to overcome a thermogravitational process, since the vertical part of the exit channel has a convection flow and thermophoresis similar to the main chamber. Thus, if the drift velocity through this channel is too low, the material to be extracted will remain at the bottom of the heat flow cell and cannot be recovered. The situation here is thus exactly the inverse of the above consideration, so that a trade-off must be found between undisturbed extraction and the lowest possible retention of the material to be extracted in the exit channel.

These considerations made us choose an inflow speed of 3.28 nl/s, resulting in a measurement extraction timescale τflow of ~13,000 s. In order to avoid a too high retention of the material, we chose an outflow speed of 0.39 nl/s, thus giving a separtion into 12% at top and bottom, leaving the remaining 76% flowing out through the middle. The value for top and bottom fractions was still kept relatively low in order to average over as little material as possible and thus to keep as close as possible to the situation present inside the heat flow cell.

To account for this systematic uncertainty, we introduced an additional error in the composition of the bottom fraction. Taking the experimental standard deviation (\({\delta }^{\exp }\)), we calculated the point on the graph for both maximal and minimal value and added/substracted an error mNa/mform = 0.02 (called δdistortion). Since the determination of the composition is concentration-dependent, we measured the bottom outflows using ion chromatography and got an average concentration of 3.8 fold the inflow concentration. The errors can be merged by addition since they are independent. The resulting ratio can then be transformed back to the corresponding pH value, resulting in a complete uncertainty, potentially non-symmetrical. The procedure is shown in more details in Supplementary Fig. 3.

We expect this additional distortion to have weak effects on the measurement everywhere except for the equimolar region. The non-linearity near the equivalence line between sodium hydroxide and formic acid makes the measured pH values vulnerable to slight differences in concentration. Around this equimolar point, nearly all molecules are present in their charged state (Na+ for mNa and HCOO− for mform). Consequently, the distortion is introduced by different retentions of these ions in the outflow channels and thus dependent on their thermodiffusive properties.

Chemical reaction networks

We closely follow the works of Rao and Esposito17. Assume we have \({{{{{{{\mathcal{N}}}}}}}}\) species Xi in the system, subject to \({{{{{{{\mathcal{R}}}}}}}}\) reactions. The ρ-th reaction is written as

$$\mathop{\sum}\limits_{i}{\nu }_{\rho +}^{i}{X}_{i}\quad \mathop{\rightleftharpoons }\limits_{{k}^{\rho -}}^{{{k}^{\rho +}}}\quad \mathop{\sum}\limits_{i}{\nu }_{\rho -}^{i}{X}_{i}.$$
(13)

where \({\nu }_{\rho \pm }^{i}\) are the stoichiometric coefficients of species Xi in the forward (+) and backward (−) direction of reaction ρ with kρ± the bare forward and backward reaction rates. The dynamical evolution of the concentration ci of species Xi in a well-mixed (zero-dimensional) system follows

$$\frac{\partial {c}_{i}}{\partial t}={\omega }_{i}=\mathop{\sum}\limits_{\rho }{\nu }_{\rho }^{i}\left({k}^{\rho +}\mathop{\prod}\limits_{i}{c}_{i}^{{\nu }_{i}^{\rho +}}-{k}^{\rho -}\mathop{\prod}\limits_{i}{c}_{i}^{{\nu }_{i}^{\rho -}}\right)=\mathop{\sum}\limits_{\rho }{\nu }_{\rho }^{i}{r}_{\rho }$$
(14)

with the reaction currentr rρ and the total reaction rate of species Xi denoted ωi. It vanishes if the species are in chemical equilibrium, described by an equilibrium constant Kρ

$${K}^{\rho }={\log }_{10}\left(\frac{{k}^{\rho +}}{{k}^{\rho -}}\right)={\log }_{10}\left(\mathop{\prod}\limits_{i}{\left({c}_{i}^{{{{{{{{\rm{eq}}}}}}}}}\right)}^{{\nu }_{i}^{\rho }}\right)$$
(15)

where \({c}_{i}^{{{{{{{{\rm{eq}}}}}}}}}\) denote (molar) concentrations in chemical equilibrium. Summarizing the stoichiometric coefficients of all (forward and backward reactions) in a matrix with elements \({\nu }_{\pm }=\{{\nu }_{\rho \pm }^{i}\}\), the stoichiometric matrix reads ν ≔ ν− − ν+ and has dimensions \({{{{{{{\mathcal{N}}}}}}}}\times {{{{{{{\mathcal{R}}}}}}}}\).

Stoichiometric algebra: conservation laws and reaction cycles

Consider an \({{{{{{{\mathcal{N}}}}}}}}\times {{{{{{{\mathcal{R}}}}}}}}\) matrix ν. Denote the the dimensions of its right (νv = 0) and left (νTw = 0) nullspaces by \({{{{{{{\mathcal{Z}}}}}}}}\) and \({{{{{{{\mathcal{C}}}}}}}}\), respectively. The rank-nullity theorem ensures that

$${{{{{{{\mathcal{Z}}}}}}}}={{{{{{{\mathcal{R}}}}}}}}-{{{{{{{\rm{rank}}}}}}}}(\nu ),\quad {{{{{{{\mathcal{C}}}}}}}}={{{{{{{\mathcal{N}}}}}}}}-{{{{{{{\rm{rank}}}}}}}}(\nu ),$$
(16)

where rank(ν) is the rank of ν. Assume we have a row vector n of size \({{{{{{{\mathcal{N}}}}}}}}\) consisting of integer values ni representing the number of instances of each species Xi present in the (well-mixed) system. In addition, we have a reaction vector ϱ of length \({{{{{{{\mathcal{R}}}}}}}}\) with integer entries ϱρ. The mapping νϱ yields the change in the number of species (ni) after carrying out the ρ-th reaction in forward direction ϱρ times. Hence, a non-zero right null-vector of ν can be interpreted as carrying out multiple reactions after which the vector n remains unchanged. This constitutes a reaction cycle. The number of independent reaction cycles is given by the dimensions of the right nullspace of ν. Each independent reaction cycle \({{{\tilde{{{{{\boldsymbol{\varrho }}}}}}}}}\) however diminishes the number of independent equilibrium constants by linearly relating them, as

$$\mathop{\sum}\limits_{\rho }{\tilde{\varrho }}_{\rho }{K}^{\rho }=\mathop{\sum}\limits_{\rho }{\tilde{\varrho }}_{\rho }\left(\mathop{\sum}\limits_{i}{\nu }_{i}^{\rho }{\log }_{10}\left({c}_{i}^{{{{{{{{\rm{eq}}}}}}}}}\right)\right)=\mathop{\sum}\limits_{i}{\log }_{10}\left({c}_{i}^{{{{{{{{\rm{eq}}}}}}}}}\right)\mathop{\sum}\limits_{\rho }{\nu }_{i}^{\rho }{\tilde{\varrho }}_{\rho }=0.$$
(17)

Complementary, a mapping νTnT yields a reaction vector ϱ which entries ϱρ give how often the ρ-th reaction needs to be carried out to change the numbers of species Xi denoted in n. A non-zero right nullvector \({{{{{{{{\boldsymbol{l}}}}}}}}}^{(j)}=({l}_{i}^{(j)})\) of νT hence defines a linear combination of species that remain unchanged by carrying out any reaction. Therefore, these linear combination define conserved quantities, which we call moeties. The number of these is given by the right nullspace of νT. Moeity concentrations \({m}^{(j)}={\sum }_{i}{l}_{i}^{(j)}{c}_{i}\) are kept constant by the reaction dynamics because l(j) is a right null-eigenvector and hence

$$\frac{\partial }{\partial t}{m}^{(j)}=\mathop{\sum}\limits_{i}{l}_{i}^{(j)}\frac{\partial {c}_{i}}{\partial t}=\mathop{\sum}\limits_{i}{l}_{i}^{(j)}{\omega }_{i}=\mathop{\sum}\limits_{i,\rho }{\nu }_{i}^{\rho }{l}_{i}^{(j)}{r}_{\rho }=\mathop{\sum}\limits_{i,\rho }\underbrace{({\nu }_{i}^{\rho }{l}_{i}^{(j)})}_{\begin{array}{c} = 0\end{array}}{r}_{\rho }=0.$$
(18)

By the rank-nullity theorem there are always \({{{{{{{\mathcal{R}}}}}}}}-{{{{{{{\mathcal{Z}}}}}}}}={{{{{{{\mathcal{N}}}}}}}}-{{{{{{{\mathcal{C}}}}}}}}\) independent equilibrium constants, which give rise to constraints of the form of Eqs. (10). In addition, there are always \({{{{{{{\mathcal{C}}}}}}}}-1\) moeties that are linearly independent from the charge moiety and thus give rise to the constraints shown in Eqs. (8). Finally, one can always use differential electroneutrality that gives rise to the single constraint as shown in Eqs. (9). As such, in general we have

$$({{{{{{{\mathcal{N}}}}}}}}-{{{{{{{\mathcal{C}}}}}}}})+({{{{{{{\mathcal{C}}}}}}}}-1)+1={{{{{{{\mathcal{N}}}}}}}}$$
(19)

independent linear equations for the \({{{{{{{\mathcal{N}}}}}}}}\) dynamical species. This fact ensures the existence and uniqueness of a solution for general chemical networks.

Chemostated system

In chemostated systems, some of the species are not considered as “dynamic” species but assumed to be set constant. In our system, water is considered a chemostated species and the corresponding equilibrium constant Kw includes this fixed concentration. Algebraically, the above statements still hold. Due to the Rank-Nullity-Theorem each chemostatted species either breaks a conservation law or creates a linear dependence between species, reducing the number of independent equilibrium constants by one. Hence, no matter the number of species chemostatted, the equations fixing the dynamical species will always match their respective number. For more details see ref. 17.

Thermogravitational accumulation

Thermophoresis

Colloidal particles travel along an external temperature gradient (thermophoresis). In the overdamped limit, this drift is written as

$${J}_{{{{{{{{\rm{DT}}}}}}}}}=-D{S}_{T}c\nabla T,$$
(20)

with T a temperature field, D the diffusion coefficient of the colloidal particle and ST its Soret coefficient, describing the coupling-strength of the particle to the temperature field. The phenomenology of thermophoretic movement can be described thermodynamically36.

2-D description of thermal traps with thermophoresis and convection

A mathematical approach modeling thermal traps was given by Debye14,15. The temporal evolution of the concentration c of a species in a trap is given by the continuity equation

$$\frac{\partial c}{\partial t}=-\nabla J$$
(21)

with the flux

$$J=-D\nabla c+\left({{{{{{{\boldsymbol{u}}}}}}}}-D{S}_{T}\nabla T\right)c.$$
(22)

In the bulk of the thermal trap the convective flow field u mainly consists of its vertical component uy with

$${u}_{y}(x)=\frac{\beta g\rho \Delta {{{{{{{\rm{T}}}}}}}}}{12\mu }\left(x-\frac{{x}^{3}}{{\left(\frac{w}{2}\right)}^{2}}\right)$$
(23)

with β, ρ, μ the material specific values for the coefficient of thermal expansion, the density and the viscosity, g the gravitational acceleration and ΔT the temperature difference across the short side of the trap with width w. The convective flow is symmetric with respect to the midpoint of the trap. The flow is directed downwards at the cold side and upwards at the hot side of the thermal trap. The average vertical velocity in one half side of the trap can then be calculated to be

$${\bar{u}}_{y}=\frac{1}{b}\int\nolimits_{0}^{b}{u}_{y}(x)=\frac{\beta g\rho \Delta {{{{{{{\rm{T}}}}}}}}}{12\mu }\int\nolimits_{0}^{b}{{{{{{{\rm{d}}}}}}}}x\left(x-\frac{{x}^{3}}{{b}^{2}}\right)=\frac{\beta g\rho \Delta {{{{{{{\rm{T}}}}}}}}}{12\mu }\frac{1}{16}{w}^{2}$$
(24)

The steady state vertical concentration profile is then found to be

$$c(y)=G\exp \left(-\frac{y}{l}\right)\qquad {{{{{{{\rm{with}}}}}}}}\qquad \frac{1}{l}=\frac{4}{15}\frac{\Delta {{{{{{{\rm{T}}}}}}}}{S}_{T}{\bar{u}}_{y}}{D+\frac{128}{315}\frac{{\left({\bar{u}}_{y}b\right)}^{2}}{D}}.$$
(25)

A logarithmic concentration difference between bottom and top then writes as

$$\Delta {\log }_{10}(c)=\frac{h}{l}{\log }_{10}(e),$$
(26)

with h the height of the trap.

Electroneutrality

In order for the bulk electroneutrality assumption to hold to good approximation, electrostatic interactions need to be the strongest forces in the system. In our case they therefore need to be compared with the charge separation processes diffusion and thermophoresis. To estimate the deviation from electroneutrality in one dimension we assume the following situation: a positively charged species is homogeneously distributed around x = 0 and a negatively charged compound is linearly distributed with concentration difference Δc at x = ± Δx. The electric field is then—according to Poissons equation—given by

$$-\nabla E=\frac{1}{\epsilon }\rho =\frac{1}{\epsilon }F({c}_{+}-{c}_{-})$$
(27)

Putting in the concentration profile depicted above we can approximate

$${c}_{-}\approx {c}_{+}+\frac{x}{\Delta x}\Delta c\quad \Rightarrow \quad \frac{{{{{{{{\rm{d}}}}}}}}E}{{{{{{{{\rm{d}}}}}}}}x}\approx \frac{F}{\epsilon }\Delta c\frac{x}{\Delta x}\quad \Rightarrow \quad E\approx \frac{F}{\epsilon }\Delta c\frac{{x}^{2}}{\Delta x}$$
(28)

the contribution to the fluxes are (disregarding diffusive fluxes)

$${J}_{DT,i}=-{D}_{i}{S}_{T,i}\frac{\partial T}{\partial x}{c}_{i}\quad {{{{{{{\rm{and}}}}}}}}\quad {J}_{el,i}={z}_{i}\frac{{D}_{i}F}{RT}E{c}_{i}$$
(29)

with the steady state condition

$${{{{{\rm{J}}}}}}\_{-}{{{{{\rm{DT}}}}}}{{"}} ={{{{{\rm{J}}}}}}\_{-}{{{{{\rm{el}}}}}}{"} \quad \iff \quad {D}_{i}{S}_{T,i}\frac{{{{{{{{\rm{d}}}}}}}}T}{{{{{{{{\rm{d}}}}}}}}x}{c}_{i}=\frac{{D}_{i}F}{RT}E{c}_{i}\iff \quad {S}_{T,i}\frac{\partial T}{\partial x}=\frac{F}{RT}\frac{F}{\epsilon }\frac{{x}^{2}}{\Delta x}$$
(30)

regarding the situation at x = Δx we get for the deviation from electroneutrality Δc

$$\Delta c=\frac{{S}_{T,i}RT\epsilon }{{F}^{2}\Delta x}\frac{\Delta {{{{{{{\rm{T}}}}}}}}}{w}\approx 1{0}^{-10}\left[{{{{{{{\rm{mol}}}}}}}}/{{{{{{{{\rm{m}}}}}}}}}^{3}\right].$$
(31)

We used F = 96485.338 C/mol, R = 8.314 J/(mol ⋅ K), ε = εrε0 = 80 ⋅ 8.854 ⋅ 10−12 F/m37. This result shows that by comparing the magnitude of the constants related to the electrostatic flux to those involved in the thermodiffusive flow, the electroneutrality condition is rendered valid. Even though our system is not homogeneous, one can use electroneutrality to calculate the electric field, as explained in more detail by Feldberg20.

Zeroth-order approximation in the 1-D case

Solving the linear Equations (8), (9) and (10) expresses the gradients as nonlinear functions of the concentrations.

$$\frac{\partial {c}_{i}}{\partial x}=-{S}_{i}^{{{{{{{{\rm{eff}}}}}}}}}(\{{c}_{k}\})\frac{\partial T}{\partial x}{c}_{i}.$$
(32)

With \({S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}\})\) may in general have some arbitrary non-linear dependence on the steady-state concentrations of (in principle) all species {ci}. We define \(\gamma ={c}_{i}-{c}_{i}^{0}\) the deviation of the steady-state concentration from the initial concentration \({c}_{i}^{0}={c}_{i}(t=0)\). The initial concentration is reached, after the constituents have chemically equilibrated. We expand \({S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }\left(\{{c}_{i}\}\right.\) around γ = 0

$${S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}\})={S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}^{0}\})+\mathop{\sum }\limits_{n=1}^{\infty }\frac{{({S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}^{0}\}))}^{(n)}}{n!}{\gamma }^{n}={S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}+{{{{{{{\mathcal{O}}}}}}}}[\gamma ]$$
(33)

For γ ≪ 1 we can make the approximation

$${S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}\})\approx {S}_{T,{{{{{{{\rm{eff}}}}}}}}}^{* }(\{{c}_{i}^{0}\})={S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}({m}_{{{{{{{{\rm{Na}}}}}}}}},{m}_{{{{{{{{\rm{form}}}}}}}}}).$$
(34)

The steady-state solution is then a exponential (with linear temperature gradient \(\frac{\partial T}{\partial x}=\frac{\Delta {{{{{{{\rm{T}}}}}}}}}{w}\), w the width, ΔT the temperature difference)

$${c}^{* }(x)={g}_{0}^{* }\exp \left(-{S}^{{{{{{{{\rm{eff}}}}}}}},0}\frac{\Delta {{{{{{{\rm{T}}}}}}}}}{w}x\right)$$
(35)

with the constant \({g}_{0}^{* }\) remains to be fixed (e.g. by global conservation of species). Since we are only interested in pH differences, \({g}_{0}^{* }\) does not play a role for calculating ΔpH.

Homogenous concentrations \({c}_{i}^{0}\)

The homogenous concentrations to be used to calculate \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}({m}_{{{{{{{{\rm{Na}}}}}}}}},{m}_{{{{{{{{\rm{form}}}}}}}}})\) are given by the steady state conditions of the well mixed chemical reaction network. Explicitly, the equations for the concentrations are:

$${K}_{a} = \,\frac{{c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}^{0}{c}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}^{0}}{{c}_{{{{{{{{\rm{HCOOH}}}}}}}}}^{0}}\\ {K}_{w} =\, {c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}^{0}{c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}^{0}\\ {m}_{{{{{{{{\rm{form}}}}}}}}} =\, {c}_{{{{{{{{\rm{HCOOH}}}}}}}}}^{0}+{c}_{{{{{{{{{\rm{A}}}}}}}}}^{-}}^{0}\\ 0 =\, {c}_{{{{{{{{{\rm{H}}}}}}}}}^{+}}^{0}-{c}_{{{{{{{{{\rm{COOH}}}}}}}}}^{-}}^{0}+{c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}^{0}-{c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}^{0}\\ {K}_{b} =\, \frac{{c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}^{0}{c}_{{{{{{{{{\rm{OH}}}}}}}}}^{-}}^{0}}{{c}_{{{{{{{{\rm{NaOH}}}}}}}}}^{0}}\\ {m}_{{{{{{{{\rm{Na}}}}}}}}} =\, {c}_{{{{{{{{{\rm{Na}}}}}}}}}^{+}}^{0}+{c}_{{{{{{{{\rm{NaOH}}}}}}}}}^{0}$$
(36)

with Ka = 10−3.745, Kb = 10−0.56, Kw = 10−14. We can always solve these equations such that we can express the concentrations \({c}_{i}^{0}\) as functions of the moeties m. Experimentally, the molar moety concentrations mform (the amount of bare formic acid) and mNa can be controlled.

Separation of timescales

The crucial assumption for the development of a hierarchical theory is the separation of timescales associated to the different dynamic processes. In the following we will give reasoning on why these assumptions are reasonable. For an overview over the timescales involved, see Supplementary Fig. 4.

Reaction timescale τ chem

For the protonation and deprotonation of simple acid-base reactions, it is known that timescales are nearly instantaneous38. As an example, this has been studied for the deprotonation of formic acid where it was confirmed that timescales are <10−3 s39.

Thermophoretic timescale τ phor

Since the steady state temperature profile across the thermal trap is linear, the velocity associated with the thermophoretic movement is

$${u}_{{{{{{{{\rm{phor}}}}}}}}}=D{S}_{T}\frac{\Delta {{{{{{{\rm{T}}}}}}}}}{w}\approx 39\cdot 1{0}^{-6}{{{{{{{\rm{m}}}}}}}}/{{{{{{{\rm{s}}}}}}}},$$
(37)

with ΔT = 39K and w = 0.17mm. Thus, the time-scale of the phoretic motion in horizontal direction is given as

$${\tau }_{{{{{{{{\rm{phor}}}}}}}}}\approx w/{u}_{{{{{{{{\rm{phor}}}}}}}}}$$

The Soret and diffusion coefficient for the hydrogen ion and the associated phoretic timescales are given in Supplementary Table 1).

Convective timescale τ conv

The average velocity of the convective flow is

$${u}_{{{{{{{{\rm{conv}}}}}}}}}={\bar{u}}_{y}=\frac{1}{16}\frac{\beta g\rho \Delta {{{{{{{\rm{T}}}}}}}}}{12\mu }{w}^{2}\approx 5.0\cdot 1{0}^{-6}{{{{{{{\rm{m}}}}}}}}/{{{{{{{\rm{s}}}}}}}}$$

where we used the values β = 69 ⋅ 10−6 1/K, g = 9.81 m/s2, ρ = 103 kg/m3 and μ = 0.80 mPa ⋅ s37. Thus, for a chamber height h = 50 mm we obtain a time-scale

$${\tau }_{{{{{{{{\rm{conv}}}}}}}}}=h/{u}_{{{{{{{{\rm{conv}}}}}}}}}\approx 10000s,$$
(38)

which is much larger than the typical phoretic time scales.

Measurement (flow) timescale τ flow

The timescale of the measurement process τflow is defined by the volume of the thermal chamber and the flow rate applied. The volume V is calculated using the height h (50 mm), the width w (170 μm) and the broadness d (5 mm), giving V = 42.5 μl. Relating to the flow rate used throughout the experiments (\(3.28\,\frac{{{{{{{{\rm{nl}}}}}}}}}{{{{{{{{\rm{s}}}}}}}}}\)), we get a timescale

$${\tau }_{{{{{{{{\rm{flow}}}}}}}}}=\frac{{{{{{{{{\rm{vol}}}}}}}}}_{{{{{{{{\rm{thermal}}}}}}}}{{{{{{{\rm{chamber}}}}}}}}}}{{{{{{{{\rm{flow}}}}}}}}\,{{{{{{{\rm{rate}}}}}}}}}\approx 13000\,{{{{{{{\rm{s}}}}}}}},$$
(39)

which is somewhat larger than the convective time-scale. Hence, we assume that the concentration dynamics in the convective setting are only slightly disturbed in the experiment.

Interpretation in 2D and 3D

Interpretation in 2D via the Debye factor

While in a purely one-dimensional case, the above expression can directly be used to calculate accumulation profiles of species, in two dimensions, convective transport has to be taken into account. We are able to make qualitative predictions about this situation since the processes happen on different timescales as shown in the section “Separation of timescales”. The initial configuration of the system is homogeneous and chemically equilibrated. As shown above, the two main transport processes, thermophoresis and convection, have similar velocities, however their timescales differ as the lengthscale for each process is different by orders of magnitude (w/h ~ 3.4 ⋅ 10−4). Hence, the concentration field is first equilibrated in the horizontal direction with the exception of the upper and lower end of the trap. Stopping the process and taking a snapshot would reveal a horizontal concentration gradient, while in vertical direction, the species would be largely distributed homogeneously. The convective flow field is zero in the middle of the trap and flows up or downwards on the hot or cold side, respectively. Consequently, species located at either side of the trap are transported upwards or downwards. The horizontal gradient established by thermophoresis within its timescale is an approximation on the magnitude of the expected vertical flow, as it imposes different levels of concentration on either side of the thermal trap. From the slope of the gradient we can therefore estimate what fraction of the total species will be transported either upwards or downwards. This net transport over time accumulates species in the vertical direction until a steady-state of the vertical transport is reached as diffusive and convective currents are balancing each other. Therefore, through the different equilibration timescales of thermophoresis and convection we can make statements about the vertical gradient by looking at the horizontal gradient. The latter in turn is proportional to \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\frac{\Delta {{{{{{{\rm{T}}}}}}}}}{w}\). Hence, by calculating \({S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\) for a given chemical reaction network we are able to make predictions about the outcome of thermal trap experiments in the full dimension.

As introduced in the main text, the effective Soret coefficient relates to the horizontal pH gradient by \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{hor}}}}}}}}}\approx \frac{\Delta T}{\ln (10)}{S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\). For the amplitude of the full 2D gradient, we use the scaling \({\left(\Delta {{{{{{{\rm{pH}}}}}}}}\right)}_{{{{{{{{\rm{vert}}}}}}}}}\approx {\alpha }_{{{{{{{{\rm{th}}}}}}}}}\cdot {S}_{{{{{{{{\rm{H}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}},0}\left({m}_{{{{{{{{\rm{Na}}}}}}}}},{m}_{{{{{{{{\rm{form}}}}}}}}}\right)\) Following the results by Debye14, we approximate the vertical concentration profile by an exponential function

$$c(y)=G\exp \left(-\frac{y}{l}\right)\quad {{{{{{{\rm{with}}}}}}}}\quad \frac{1}{l}=\frac{4}{15}\frac{\Delta TS{\bar{u}}_{y}}{D+\frac{128}{315}\frac{{\left({\bar{u}}_{y}b\right)}^{2}}{D}}.$$

A logarithmic concentration difference between bottom and top then gives \(\Delta {\log }_{10}(c)=\frac{h}{l}{\log }_{10}(e)\) so we can write the factor αth

$${\alpha }_{{{{{{{{\rm{th}}}}}}}}}\approx \frac{\Delta T}{\ln (10)}\cdot \frac{4}{15}\frac{h{\bar{u}}_{y}}{D+\frac{128}{315}\frac{{\left({\bar{u}}_{y}\frac{w}{2}\right)}^{2}}{D}},\quad {{{{{{{\rm{where}}}}}}}}\quad {\bar{u}}_{y}=\frac{\beta g\rho \Delta {{{{{{{\rm{T}}}}}}}}}{12\eta }\frac{1}{16}{w}^{2}$$
(40)

With thermal expansion coefficient β = 207 ⋅ 10−6 1/K, gravitational constant g = 9.81 m/s2, density of water ρ = 995.67 kg/m3 (at 30 ∘C), viscosity η = 797 ⋅ 10−6 mPa ⋅ s, temperature difference ΔT = 39 K, height of trap h = 0.05 m, width of trap w = 170 ⋅ 10−6 m. Influences of formic acid and sodium hydroxide on density and viscosity can be neglected. As diffusion coefficient, we take DH from Supplementary Table 1. We take the values for 30 ∘C as most material is accumulated towards the colder side. This gives us an αth of 358.5, used in the main text, Fig. 3.

Extrapolation to 3D and flow distortions

In the experimental part however, we measure the pH gradient in a 3D setting, continuously extracting the fluid through 3 outlets which we want to compare to the theoretical predictions. As discussed above, there are multiple uncertainties linked to the experimental setup. In addition and as mentioned before, the measured pH values on the top and bottom outfluxes are averaged over 12 % of the length of the thermal trap. Depending on the specific arrangement of each concentration profile this averaging procedure alters the concentration ratios of each dissolved compound at the outfluxes.

Impact of chemical reactions, electrostatics and temperature dependent reaction rates

For a better understanding of the individual contributions from chemical reactions, electrostatics and the temperature dependence of reaction rates, we simulated the chemical system in a 1 dimensional finite-element simulation (Comsol 5.4, see Supplementary Data 1). For a detailed study, we had to restrict ourselves to the 1D case since simulations for the 2D or 3D case are not converging when including electrostatic interactions between solutes according to our best knowledge.

For this, we combined the modules “heat transfer in solids”, “general form PDE” and “electrostatics”. In the stationary state and under assumption of insulation, the heat transfer is calculated from

$$\rho \cdot {{{{{{{{\rm{C}}}}}}}}}_{{{{{{{{\rm{p}}}}}}}}}\cdot {{{{{{{\bf{u}}}}}}}}\cdot {{{{{{{\boldsymbol{\nabla }}}}}}}}{{{{{{{\rm{T}}}}}}}}+{{{{{{{\boldsymbol{\nabla }}}}}}}}\cdot \left(-{{{{{{{\rm{k}}}}}}}}\cdot {{{{{{{\boldsymbol{\nabla }}}}}}}}{{{{{{{\rm{T}}}}}}}}\right)=Q$$
(41)

with the density ρ, the specific heat capacity Cp, the velocity of the fluid u, the temperature T, the thermal conductivity \({{{{{{{{\rm{k}}}}}}}}}_{{{{{{{{{\rm{H}}}}}}}}}_{2}{{{{{{{\rm{O}}}}}}}}}=0.62\frac{{{{{{{{\rm{W}}}}}}}}}{{{{{{{{\rm{mK}}}}}}}}}\) of water and the heat flux Q. Assuming a very slow fluid velocity, the first term can be neglected.

The result is then coupled to a general PDE and electrostatics. The former gives the following equation:

$${e}_{a}{\partial }_{t}^{2}{{{{{{{\bf{c}}}}}}}}+{d}_{a}{\partial }_{t}{{{{{{{\bf{c}}}}}}}}+\nabla \Gamma =f$$
(42)

with the mass coefficients ea, the concentration vector c = [cH, cA, . . ], the damping coefficients da, the flux Γ and the source term f. In our case, the matrix ea is zero. The flux writes as follows:

$$\Gamma =-{D}_{i}\cdot {c}_{i}-{S}_{T,i}\cdot {D}_{i}\cdot {c}_{i}\cdot \Delta T-\frac{{z}_{i}\cdot {D}_{i}\cdot {F}_{{{{{{{{\rm{const}}}}}}}}}}{{R}_{{{{{{{{\rm{const}}}}}}}}}\cdot T}\cdot \Delta V\cdot {c}_{i}$$
(43)

with temperature T, electric potential V, gas constant \({R}_{{{{{{{{\rm{const}}}}}}}}}\) and Faraday constant \({F}_{{{{{{{{\rm{const}}}}}}}}}\). For each species i, the concentration (ci), the charge (zi) the diffusion coefficient (Di), and the Soret coefficient (ST,i) are used, for the latter see Supplementary Table 1. The source term includes all reactions, for example in the case of formic acid (AH):

$${f}_{{{{{{{{\rm{AH}}}}}}}}}=-{k}_{on}\cdot {c}_{{{{{{{{\rm{AH}}}}}}}}}+{k}_{off}\cdot {c}_{{{{{{{{\rm{H}}}}}}}}}\cdot {c}_{{{{{{{{\rm{A}}}}}}}}}$$
(44)

For the temperature dependence of the dissociation constants of water (KW) and formic acid (KA), we used the values from40 for formic acid and41 for water.

For the electrostatics, the equations write as follows:

$${{{{{{{\boldsymbol{\nabla }}}}}}}}\cdot {{{{{{{\bf{D}}}}}}}}={\rho }_{V}\qquad {{{{{{{\rm{and}}}}}}}}\qquad {{{{{{{\bf{E}}}}}}}}=-{{{{{{{\boldsymbol{\nabla }}}}}}}}V$$
(45)

with the electric displacement D = ϵ0ϵrE (including the permittivities), the electric field E, the relative permittivity ϵr, the vaccum permittivity ϵ0, the electric potential V and the space charge density ρV which writes as follows:

$${\rho }_{V}={F}_{const}\cdot \mathop{\sum}\limits_{i}{c}_{i}\cdot {z}_{i}$$
(46)

To better understand the individual contributions of electrostatics, temperature dependence etc, we turned them off one by one (Supplementary Fig. 5).