Introduction

Quantum spin liquid (QSL) is a state of matter that exhibits exotic fractional excitations and long-range entanglement without symmetry breaking1,2,3,4. Since Anderson’s proposal of the prototype, i.e., resonating-valence-bond (RVB) state, in 19735, QSL has been attracting researchers for decades, due to its key role in understanding high-temperature superconductivity6 and the possible realization of the topological quantum computation7. Experimentally, many prominent two-dimensional QSL candidate compounds have been extensively studied (the one-dimensional scenario of QSL is qualitatively different2), including the kagome-lattice ZnCu3(OH)6Cl2 (herbertsmithite)8,9,10,11,12,13,14,15,16,17, triangular-lattice κ-(ET)2Cu2(CN)318,19, EtMe3Sb[Pd(dmit)2]220,21, YbMgGaO422,23, etc., all of which generally exhibit gapless QSL behaviors9,11,14,16,18,19,20,22,24,25,26,27, but without evident magnetic thermal conductivity28,29,30,31,32.

Despite the progress, the existing experimental evidence for QSL remains circumstantial and strongly depends on theoretical interpretation. The root cause lies in the quenched interaction randomness introduced by structural imperfection that is inevitable in all real materials2,17,33. Therefore, great efforts are being devoted to exploring for ultrahigh-quality candidate materials, which is extremely challenging2. On the other hand, disorder-free QSL, even if successfully prepared, is usually very fragile. For instance, the most frustrated kagome Heisenberg antiferromagnet (KHA) falls back to conventional long-range magnetic ordering in the presence of a weak next-nearest-neighbor coupling ∣J2∣ ≥ 0.03J134 or Dzyaloshinsky-Moriya interaction ∣D∣ ≥ 0.012J135. These constrictions further compress the “living space” of disorder-free perfect QSL compounds.

Alternatively but more realistically, one could first find out whether the inherent randomness is fatal or vital to the QSL physics4. In fact, this same question can also be raised for high-temperature superconductivity, as it is generally believed that Cooper pairs naturally form once the RVB states are charged upon chemical doping6,36. The presence of quenched vacancies in the KHA can lead to a valence bond glass ground state (GS)37. Further, Kawamura et al. found that randomness-induced QSL GSs instead of spin glasses form in both KHA and triangular Heisenberg antiferromagnet with strong bond randomness, ΔJ/J1 ≥ 0.4 and 0.638,39, respectively, which may explain the gapless behaviors observed in ZnCu3(OH)6Cl2, κ-(ET)2Cu2(CN)3, EtMe3Sb[Pd(dmit)2]233, etc. Later similar scenarios have been generally applied to the gapless QSL behaviors observed in the strongly-spin-orbital-coupled triangular-lattice YbMgGaO440,41 with the mixing of Mg2+/Ga3+26,42, as well as in other relevant materials43. Despite the growing interest in theory, the key issue is whether the paramagnetic phase conspired by frustration and randomness in real materials is relevant to the exotic QSL/RVB state with strong quantum fluctuations, or simply a trivial product state of quenched random singlets. To address this issue, local and dynamic measurements on QSL candidates with quantifiable randomness are particularly needed.

Recently, a S = 1/2 KHA YCu3(OH)6.5Br2.5 (YCOB) has been proposed, without any global symmetry reduction of the kagome lattice (space group \(P\bar{3}m1\), see Fig. 1d)44,45,46. Neither long-range magnetic ordering nor spin-glass freezing was observed down to 50 mK ~ 0.001〈J1〉, as evidenced by specific heat46, thermal conductivity47, and ac susceptibility44,45 measurements. The observed power-law T dependence of low-T specific heat suggests the appearance of gapless spin excitations44,46. Unlike other known QSL materials (e.g. ZnCu3(OH)6Cl214,15,16,48,49), the mixing between Cu2+ and other nonmagnetic ions is prohibited due to the significant ionic difference, thus defect orphan spins are essentially negligible44. Further, the antisite mixing of the polar OH− and nonpolar Br− causes 70(2)% of randomly distributed hexagons of alternate exchanges (e.g. Fig. 1b) on the kagome lattice (Fig. 1d), which accounts for the measured thermodynamic properties above T ~ 0.1〈J1〉44. Therefore, YCOB provides an excellent platform for a quantitative study of the aforementioned randomness-induced QSL physics.

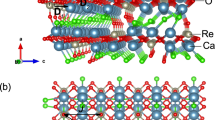
Fig. 1: Crystal structure of YCu3(OH)6.5Br2.5 around the kagome layer of Cu2+.
figure 1

The Br1 nuclear (81Br or 79Br) spin detects three equidistant Cu2+ electronic spins of each triangle on the kagome lattice (a), and the inset defines the coordinate system for the spin components. Whereas, the Br2 nuclear spin mainly probes the nonsymmetric hexagon of spins with alternate exchanges (b), instead of the symmetric hexagon with almost uniform exchange (c). The formation energies of b and c stacking sequences are listed, and the different exchange paths of Cu-O-Cu (J1a, J1b, and J1c, depending on the bond angles) are marked. The principal axes of the electric field gradient calculated by density functional theory at the Br1 (a) and Br2 (b) sites are displayed by arrows scaled by the modulus of the tensor element, Vzz ~ − 2Vxx ~ − 2Vyy (Supplementary Note 6). In our measurements, the external magnetic field is always applied along the z axis, and thus the second-order quadrupole shifts of the main NMR lines are negligibly small. d The crystal structure determined by the single-crystal x-ray diffraction44. The thin lines mark the unit cell.

Full size image

Herein, the effect of inherent randomness on the QSL properties was investigated locally by 81Br and 79Br nuclear magnetic resonance (NMR) measurements on high-quality YCOB single crystals. We successfully identify the two NMR signals originating from the intrinsic kagome spins (Br1, see Fig. 1a) and spins of hexagons with alternate exchanges on the kagome lattice (Br2, see Fig. 1b). Simulations of the random exchange model show good agreement with the measured T dependence of NMR line shifts and broadening, which suggests the formation of the randomness-induced QSL phase at low T. The measured in-plane spin fluctuations of the kagome spin system exhibit a weak power-law T dependence down to T ~ 0.03〈J1〉 despite the quenched exchange randomness, thus supporting the survival of strong quantum fluctuations in YCOB.

Results

NMR spectra

Figure 2a shows the 81Br NMR spectra measured on the crystal S1 (Supplementary Fig. 1) at μ0H∥ ~ 10.75 T (~0.14〈J1〉). Two well-separated peaks are observed, originating respectively from two different Wyckoff positions of 2d (Br1) and 1a (Br2). Above ~15 K, the ratio between the integrated intensities of these two peaks IBr2/IBr1 ~ 0.2 is well consistent with the stoichiometric ratio of Br2 and Br1 determined by single-crystal x-ray diffraction (XRD) fBr2/fBr1 = 0.22(1)44 (see inset of Fig. 2b). Below 15 K, the weight of Br1 NMR line decreases drastically and IBr2/IBr1 increases sharply, due to the reduced spin-spin relaxation times (Supplementary Note 4 and Supplementary Fig. 5)50. Neither Br1 nor Br2 peak splits down to 1.7 K, suggesting the absence of conventional magnetic ordering within the ability of our resolution.

Fig. 2: Nuclear magnetic resonance spectra of YCu3(OH)6.5Br2.5.
figure 2

a Frequency-sweep spectra measured on the sample S1 at a field μ0H∥ ~ 10.75 T (the reference frequency f0 = 81γnμ0H∥ ~ 123.64 MHz). The shifts of two lines, K1 and K2, are marked by solid and hollow triangles, respectively. Temperature dependence of K1 (b) and K2 (c), with the bulk magnetization (〈Sz〉) measured at μ0H∥ = 10.75 T for comparison. The inset of b shows the ratio between the integrated intensities of 81Br2 and 81Br1 lines (IBr2/IBr1), as well as the stoichiometric ratio from x-ray diffraction44. Inset of c displays K1 and K2 shifts vs bulk susceptibility χ∥ (i.e. M∥/H∥). The red bars display the normalized frequency regions where the intensity is larger than half of the maximum value in b and c, and error bars on IBr2/IBr1 show a standard error from the fit.

Full size image

The NMR shift of Br1 (K1) detecting three (z1 = 3) equidistant spins of each triangle on the kagome lattice (Fig. 1a), follows the bulk susceptibility χ∥ measured at the same magnetic field strength in the full temperature range (Fig. 2b), compatible with the absence of defect orphan spins in YCOB. In contrast, the NMR shift of Br2 (K2) shows an obvious deviation from the bulk susceptibility below ~100 K ~ 2〈J1〉. Generically, the NMR shift consists of a T-dependent term proportional to the local susceptibility and a T-independent term (K0). Above 100 K, the NMR line broadening is insignificant (Fig. 2) and the calculated local magnetization is nearly spatially homogeneous (Fig. 3a), and thus one expects a scaling law K = Ahfχ∥ + K0, where Ahf presents the hyperfine coupling between Br (Br1 or Br2) nuclear and Cu2+ electronic spins. By fitting the experimental data (see inset of Fig. 2c), we obtain Ahf1 = −0.68(2) T/μB, K01 = −0.015(7)% and Ahf2 = 0.55(3) T/μB, K02 = 0.02(1)%. The presence of both negative and positive hyperfine couplings of the same nuclear species is surprising, and the underlying mechanism must be complex, including both the positive and negative contributions.

Fig. 3: Simulations of the spatially inhomogeneous susceptibility probed by nuclear magnetic resonance (NMR) spectra.
figure 3

a Temperature dependence of NMR shifts K1 and K2, as well as bulk 〈Sz〉 measured in a vibrating sample magnetometer at a field μ0H∥ = 10.75 T. The colored lines show the calculated average 〈Sz〉 over all the triangles (\(\overline{\langle {S}_{{{{{{{{\rm{t}}}}}}}}}^{z}\rangle }\)), nonsymmetric hexagons (\(\overline{\langle {S}_{{{{{{{{\rm{nh}}}}}}}}}^{z}\rangle }\)), and symmetric hexagons (\(\overline{\langle {S}_{{{{{{{{\rm{sh}}}}}}}}}^{z}\rangle }\)). b, c The finite-temperature Lanczos diagonalization results of local magnetization of triangles (\(\langle {S}_{{{{{{{{\rm{t}}}}}}}}}^{z}\rangle\)) and nonsymmetric hexagons (\(\langle {S}_{{{{{{{{\rm{nh}}}}}}}}}^{z}\rangle\)), along with the measured K1 and K2, respectively. d Calculated local correlations of the selected spin pairs (e, f) as function of normalized temperature T/〈J1〉. e Calculations of a sample within the random kagome Heisenberg antiferromagnet (KHA) model at T = 0.1〈J1〉 and μ0H∥ = 10.75 T. The solid circles and squares stand for local magnetization \(\langle {S}_{i}^{z}\rangle\) at the kagome site i and correlation function 〈Si ⋅ Sj〉 of the nearest-neighbor spin pair 〈ij〉, respectively. f The same calculations as in e, but within the ideal KHA model. The dashed lines mark the clusters with periodic boundary conditions, and J1a, J1b, J1c, and J1 present the exchange couplings. The color scale in b and c quantifies the distributed density, whereas the ones in e and f quantify the local magnetization (circles) and correlation function (squares), respectively. The bars in a–c show the regions where the intensities are larger than half of the maximum value.

Full size image

The NMR shift of Br2 probes spins of hexagons on the kagome lattice (Fig. 1b,c), but is obviously smaller than Ahf2χ∥ (K02 ≪ K2) below 100 K (Fig. 2c). In fact, the formation energy of the optimized nonsymmetric Br2-OH2 stacking sequence (Fig. 1b) (−37.8 eV/FU), is ~ 2.5 × 104 K/FU lower than that of the symmetric Br2-Br2 configuration (Fig. 1c) (−35.7 eV/FU). Therefore, Br2 ions actually prefer the nonsymmetric local environments, and Br2 nuclear spins mainly probe the nonsymmetric hexagons with alternate exchanges44 (J1a > J1c) as illustrated in Fig. 1b. Intuitively, the nonsymmetric hexagon tends to locally release the frustration and form three nonmagnetic singlets along the stronger couplings J1a (Fig. 3e), which accounts for the relatively smaller Br2 shifts observed below 100 K (Fig. 3a). Moreover, the Br1 line detects the site susceptibility/magnetization of all the Cu2+ spins with exchange couplings J1a, J1b, and J1c, whereas the Br2 line mainly probes the hexagons of spins only with J1a and J1c. The Br2 line probes less kinds of Cu2+ spins, and thus is narrower than the Br1 line.

Quantitatively, the temperature dependence of both Br1 and Br2 shifts can be reproduced by the average magnetization of all the triangles and nonsymmetric hexagons on the kagome lattice, viz. \({K}_{1} \sim {A}_{{{{{{{{\rm{hf1}}}}}}}}}{g}_{\parallel }\overline{\langle {S}_{{{{{{{{\rm{t}}}}}}}}}^{z}\rangle }/({\mu }_{0}{H}_{\parallel })\) and \({K}_{2} \sim {A}_{{{{{{{{\rm{hf2}}}}}}}}}{g}_{\parallel }\overline{\langle {S}_{{{{{{{{\rm{nh}}}}}}}}}^{z}\rangle }/({\mu }_{0}{H}_{\parallel })\), respectively (Fig. 3a), with J1a = 89 K, J1b = 48 K, and J1c = 16 K (〈J1〉 ~ 51 K) experimentally determined by bulk susceptibilities (Supplementary Note 1 and Supplementary Fig. 2). Taking all the triangles and nonsymmetric hexagons into account, we are able to simulate the broadening of both Br1 and Br2 lines by introducing the distributed density ∝ dnS(〈Sz〉)/d〈Sz〉 (Fig. 3b, c), where dnS(〈Sz〉) is the number of triangles or nonsymmetric hexagons with the local magnetization (per site) ranging from 〈Sz〉 to 〈Sz〉 + d〈Sz〉. 〈Sz〉 is thermally averaged, so the distributed density is a function of T.

The simulations also enable us to revisit the correlation functions 〈Si ⋅ Sj〉 in this KHA system with randomness. Compared to the ideal case (Fig. 3f), a small fraction (~3/54) of well-defined singlets with 〈Si ⋅ Sj〉 ~ − 0.7 → − 0.75 are frozen at low T in YCOB (Fig. 3e), which is a signature of releasing frustration due to the quenched randomness. These local singlets might confine the mobile spinons27,37,51,52, which might be responsible for the absence of large magnetic thermal conductivity observed in nearly all of the existing gapless QSL candidates, including the well-known ZnCu3(OH)6Cl228,29, EtMe3Sb[Pd(dmit)2]230,31, etc. However, the majority of antiferromagnetic interactions remain not fully satisfied at low T (Fig. 3d, e), and the GS wavefunction should be represented by a superposition of various pairings of spins. It is worth to mention that the weights of different pairings should be different due to the quenched randomness. The survival of strong frustration in the S = 1/2 random KHA speaks against the product GS wavefunction of randomly distributed singlets, and may still give rise to strong quantum fluctuations. To testify this, we turn to the spin dynamics of YCOB mainly probed by the spin-lattice relaxation rates as follow.

Spin dynamics

The representative spin-lattice relaxation data measured on YCOB are displayed in Fig. 4a and b, which can be well fitted to the single-exponential function for the central transition of I = 3/2 nuclear spins, i.e.,

$$M(t)={M}_{0}-2{M}_{0}F\left(\frac{1}{10}{{{{{{{{\rm{e}}}}}}}}}^{-\frac{t}{{T}_{1}}}+\frac{9}{10}{{{{{{{{\rm{e}}}}}}}}}^{-\frac{6t}{{T}_{1}}}\right),$$
(1)

where M0 and F are scale parameters for intensity. Alternatively, the relaxation data may be fitted with the stretched-exponential one,

$$M(t)={M}_{0}-2{M}_{0}F\left[\frac{1}{10}{{{{{{{{\rm{e}}}}}}}}}^{-{\left(\frac{t}{{T}_{1}}\right)}^{\beta }}+\frac{9}{10}{{{{{{{{\rm{e}}}}}}}}}^{-{\left(\frac{6t}{{T}_{1}}\right)}^{\beta }}\right].$$
(2)

Here, the stretching exponent β slightly decreases at low temperatures (see inset of Fig. 4b), but remains large down to the lowest temperature of 1.7 K, β > 0.8. Moreover, the fit to the single T1 function (i.e. β = 1) is still good even at 1.7 K (Fig. 4b), with the adj. R2 = 0.99753. The inclusion of the additional fitting parameter β only slightly improves the fit (the adj. R2 increases to 0.998), and even makes the standard error on T1 larger. Therefore, all the following T1 data are obtained with the single-exponential fits.

Fig. 4: Nuclear spin-lattice relaxation of YCu3(OH)6.5Br2.5.
figure 4

a A representative T = 2.8 K spin-lattice relaxation of Br1 measured by an inversion recovery method, fitted to the stretched-exponential function with fixing β = 1 (red) and tuning β (blue). The pulse sequence for T1 measurements is depicted in the inset. b The same fits to the relaxation data measured at other selected temperatures. The inset shows the fitted stretching exponent β. c Temperature dependence of 81Br1 nuclear spin-lattice relaxation rate 1/T1 measured on the sample S1 at a field μ0H∥ = 10.75 T, as well as 81Br1 and 79Br1 1/T1 measured on S2 at μ0H∥ = 10.75 and 11.59 T, respectively. The colored lines present the power-law fits to the experimental data below ~ 10 K ~ 0.2〈J1〉, the dashed black and blue lines are the 1/T1 and energy (per site), respectively, calculated by using the random kagome Heisenberg antiferromagnet model of YCu3(OH)6.5Br2.5. d The Curie (~T−1, black lines) and critical (~(T − Tc)\({}^{-\alpha ^{\prime} -1}\), the critical temperature Tc = − 0.1 ± 0.4 K, green lines) fits to 1/(T1T) at 1.7 ≤ T ≤ 300 K. The blue line is the low-T power-law dependence as shown in c. The inset shows the T1T vs T plot, where the dashed violet line displays the antiferromagnetic Curie-Weiss behavior (T1T ~ T + 〈J1〉, with coupling 〈J1〉 ~ 50 K). The T1 data presented in c and d are obtained from the single-exponential fits (i.e., β = 1, see a and b), and the stretched-exponential fits are made only for comparison in a and b. Error bars on the experimental data points show a standard error from fit, and the error bars in a and b are small.

Full size image

Figure 4c shows the results of Br1 nuclear spin-lattice relaxation rates (1/T1). Br1 1/T1 is highly sensitive to the electronic spin fluctuations perpendicular to the applied magnetic field on the kagome layer via the hyperfine coupling39,54,55,56,

$$\frac{1}{{T}_{1}} \sim \frac{T}{h{f}_{0}}\mathop{\sum}\limits_{{{{{{{{\boldsymbol{q}}}}}}}}}\chi ^{\prime\prime} ({{{{{{{\boldsymbol{q}}}}}}}},{f}_{0}) \sim \frac{\pi {\gamma }_{{{{{{{{\rm{n}}}}}}}}}^{2}{A}_{{{{{{{{\rm{hf1}}}}}}}}}^{2}{g}_{\perp }^{2}}{Z}\mathop{\sum}\limits _{{{{{{{{\boldsymbol{q}}}}}}}},m,m^{\prime} }{{{{{{{{\rm{e}}}}}}}}}^{-\frac{{E}_{m}}{{k}_{{{{{{{{\rm{B}}}}}}}}}T}}\\ \times | \langle m^{\prime} | {S}_{{{{{{{{\boldsymbol{q}}}}}}}}}^{\perp }| m\rangle {| }^{2}\delta \left({f}_{0}-\frac{{E}_{m^{\prime} }-{E}_{m}}{h}\right),$$
(3)

where the q dependence of Ahf1 is neglected, f0 = γnμ0H∥ ( ≪ kBT/h) → 0 presents the NMR frequency, \({S}_{{{{{{{{\boldsymbol{q}}}}}}}}}^{\perp }\) is the Fourier transform of \({S}_{i}^{\perp }\) over all triangles, and \(Z={\sum }_{m}\exp (-{E}_{m}/{k}_{{{{{{{{\rm{B}}}}}}}}}/T)\) the partition function. In our simulation of 1/T1, the delta function is replaced by a Gaussian distribution with narrow width ~ 10−4〈J1〉/h39,56.

At high temperatures (T ≫ 〈J1〉), the Moriya paramagnetic limit yields the T-independent \(1/{T}_{1}^{\infty }={(2\pi )}^{1.5}{\gamma }_{{{{{{{{\rm{n}}}}}}}}}^{2} {A}_{{{{{{{{\rm{hf1}}}}}}}}}^{2}{g}_{\perp }^{2}S(S+1)/(3{z}_{1}{\nu }_{e}) \sim 300\,{{{{{{{{\rm{s}}}}}}}}}^{-1}\), reasonably comparable with the observation (Fig. 4c), where \({\nu }_{e}=\langle {J}_{1}\rangle \sqrt{2zS(S+1)/3}/h\) is the exchange frequency with the coordination number z = 455,57,58. Upon cooling, 1/T1 slightly decreases first and then rises at T ~ 〈J1〉. These features are qualitatively reproduced by the random KHA model of YCOB (Fig. 4c). It is challenging to precisely simulate 1/T1, possibly due to the neglecting of the q dependence of Ahf55. At T = 15 K ~ 0.3〈J1〉, a weak anomaly (kink) of 1/T1 is observed, coinciding with the saturation of local nearest-neighbor correlations 〈Si ⋅ Sj〉 (Fig. 3d). This is possibly attributed to the emergence of short-range spin correlations, as seen in κ-(ET)2Cu2(CN)3, PbCuTe2O6, etc.50,59,60,61.

Discussion

As T further decreases below ~ 10K ~ 0.2〈J1〉, 1/T1 exhibits a weak enhancement, 1/T1 ~ T−α with α ~ 0.20 ± 0.02, at least down to 1.7 K ~ 0.03〈J1〉. This weak enhancement of 1/T1 is well reproducible between different single-crystal samples, nuclear spin probes (81Br and 79Br), and applied magnetic fields (μ0H∥ = 10.75 and 11.59 T), as shown in Fig. 4. It is necessary to mention that the similar slowing down of spin fluctuations was also reported in other quantum disordered spin systems62,63. Such a behavior of 1/T1 suggests the spin system of YCOB may be proximate to a gapless/critical QSL state or highly dynamic valence bond glass with long-range fluctuating singlets:

First, such a temperature dependence of 1/T1 is inconsistent with conventional glassy spin freezing. Glassy freezing is typically observed by NMR as a broad peak in 1/T1 vs T when the inverse correlation time matches the NMR frequency, and such a peak (T1 minimum) defines the freezing temperature Tc64,65,66. Moreover, 1/T1 is usually expected to increase by more than one order of magnitude at Tc from that above Tc64,65,66. However, such a robust peak in 1/T1 vs T is absent in YCOB, as shown in Fig. 4c. Other NMR quantities, line width and 1/T2 (Supplementary Fig. 6), also exhibit the common features of well-reported QSL candidates15,20,50,60,67,68, and speak against the existence of well-defined Tc in YCOB (Supplementary Note 5). Note that other experiments, including magnetic and thermodynamic measurements44,45,46, also have precluded the possibility of conventional magnetic transition. Thereby, the formation of short-range spin correlations (i.e., 〈Si ⋅ Sj〉 < 0) should be responsible for the broadening of NMR lines and enhancement of 1/T1 and 1/T2 observed at low temperatures in YCOB.

Second, classical spin fluctuations are driven by thermal energy kBT, and cease at low temperatures, T ≪ 〈J1〉1. A real example can be the S = 5/2 KHA Li9Fe3(P2O7)3(PO4)2, where the slowing down of classical spin fluctuations, 1/T1 ~ T−1, observed just above the antiferromagnetic transition temperature58, increases much faster than that seen in YCOB, upon cooling. Therefore, the observation of 1/T1 ~ T−0.20±0.02 suggests that quantum fluctuations must play an important role at low temperatures (T≤0.1〈J1〉) in YCOB.

Third, below T ~ 0.1〈J1〉, the calculated local nearest-neighbor correlations (Fig. 3d) for the spin system of YCOB level off, manifesting that the observed quantum critical slowing down of spin fluctuations (i.e., \(1/{T}_{1} \sim {(T-{T}_{{{{{{{{\rm{c}}}}}}}}})}^{-0.20\pm 0.02}\) with Tc ~ 0 K) are associated with a gapless nature of the spin excitations. This is further supported by the nearly quadratic T dependence of specific heat (C ~ T2.31)44. In contrast, an exponential T-dependent decrease of 1/T1 and C with a spin gap of ≥J1c ~ 16 K would be expected upon cooling, if the simple product GS of fully quenched random nearest-neighbor singlets is established at low T.

Finally, the system energy gets nearly T-independent (Fig. 4c) and the measured residual spin entropy is small ~ 3.4%Rln244, indicating approaching to the disordered GS properties of YCOB at ~ 1.7 K. We notice that although the temperature decreases by more than two orders of magnitude from 300 to 1.7 K, 1/T1 only slightly increases from ~ 380 to 500 s−1, thus suggesting the survival of ~ 70% of total spin fluctuations at low temperatures (i.e. quantum fluctuations)24,54,63,67. Since 1/T1 only weakly depends on temperature in the full temperature range between 1.7 and 300 K, 1/(T1T) ∝ ∑qχ″(q, f0) (see equation (3)) follows a Curie behavior diverging towards T = 0 K, as shown in Fig. 4d. We also fit the data with the critical function, 1/(T1T) ~ (T − Tc)\({}^{-\alpha ^{\prime} -1}\), in the full temperature range, and find Tc = − 0.1 ± 0.4 K ~ 0 K and \(\alpha ^{\prime}\) = 0.11(5) (see the green lines in Fig. 4d). The dynamical susceptibility (∑qχ″(q, f0)) relates to the second derivative of the free energy, and thus the observation of Tc ~ 0 K (Fig. 4d) indicates a quantum critical behavior. In the paramagnetic limit (T → ∞), the spin fluctuations including the extremely strong thermal fluctuations (∝T, see ref. 1) take huge values for an arbitrary spin system. In YCOB, nearly the same Curie behavior, 1/(T1T) ∝ ∑qχ″(q, f0) ∝ 1/T, persists from 300 K ≫ 〈J1〉 down to 1.7 K ~ 0.03〈J1〉 (Fig. 4d), thus supporting the survival of strong spin fluctuations toward zero temperature (i.e. quantum fluctuations). All together, these features are in line with the spin dynamics of the putative gapless/critical QSL or dynamic valence bond glass with long-range fluctuating singlets.

We have investigated the local spin susceptibility and dynamics by Br NMR measurements on the high-quality single crystals of YCOB whose randomness has been quantified. The quenched exchange randomness gives rise to the spatially inhomogeneous susceptibility, which accounts for the different T dependencies of Br1 and Br2 main line shifts, as well as broadening. Despite a small fraction of frozen random singlets, the majority of spins of YCOB evade conventional magnetic ordering and remain highly fluctuating, as evidenced by the weak power-law T dependence of 1/T1 down to T ~ 0.03〈J1〉. Our work highlights the role of quantum fluctuations to the gapless QSL behaviors generally observed in relevant materials with inevitable randomness.

Methods

NMR measurements

Two single-crystal samples of YCOB (S1 and S2 with ~ 6.2 and 15.2 mg, respectively) used in NMR measurements were grown by a recrystallization in a temperature gradient44. The 81Br (81γn = 11.4989 MHz/T) and 79Br (79γn = 10.6675 MHz/T) NMR measurements were performed using standard spin echo sequences at external magnetic fields ~ 10.75 and 11.59 T aligned to the c axis, between 300 and 1.7 K (the base temperature of our setup). Main NMR shifts of both Br1 and Br2 are derived from the central transitions recorded by a stepped frequency sweep ranging 121–125 MHz wherein no satellite transitions from Br can be observed due to the large nuclear quadrupole frequency νQ > 20 MHz (Supplementary Note 2 and Supplementary Fig. 3). However, the element of the electric field gradient (EFG) tensor Vzz is nearly parallel to the external field, and thus the second-order quadrupole shift is negligibly small (Supplementary Note 6 and Supplementary Figs. 7 and 8). Spin-lattice (1/T1) and spin-spin (1/T2) relaxation rates are investigated on Br1 site, measured in inversion recovery and Hahn spin-echo decay methods, respectively (Supplementary Note 3 and Supplementary Fig. 4). The error bars on T1 come from the standard nonlinear curve fits by using the Origin program, as shown in Fig. 4.

Simulations

We conducted the finite-temperature Lanczos diagonalization simulations of the random KHA model44 for the NMR line shifts and broadening, local magnetization and correlation, as well as 1/T1. No significant finite-size effect of the calculation was observed down to T ~ 0.1〈J1〉44. The formation energy (Fig. 1) is calculated as E(YCu3(OH)6+xBr3−x) − μ(Y) − 3μ(Cu) − (6 + x)μ(OH) − (3 − x)μ(Br), where the total energy is obtained from the previous density functional theory calculation44, and μ(Y), μ(Cu), μ(OH), μ(Br) are the chemical potentials of the constituents. The international system of units is used throughout this paper, and 〈〉 presents thermal and sample average.