Enhanced chiroptical responses through coherent perfect absorption in a parity-time symmetric system

Abstract

Coherent amplification of chiroptical activity from a molecularly-thin optically-active substance has been a long-standing challenge due to the inherently weak nature of chiral responses. Here we report how a coherent perfect absorber (CPA) enabled by an achiral optical system obeying parity-time (PT) symmetry has an enhanced ability to effectively sense molecular chirality of monolayered substances. We demonstrate that such a CPA-based PT-symmetric system enables us in complete darkness to probe a subtle signal change induced by the introduction of a small disturbance, such as adsorbed chiral monolayer, to the unperturbed PT-symmetric system, and allows for absolute measurement and quantitative detection of the magnitude and sign of both real and imaginary parts of the chirality parameter in a background-free environment. Moreover, the CPA-based PT-symmetric system also exhibits three orders of magnitude enhancement in chiroptical responses of molecules, which is consistent with analytical calculations of differential absorption.

Introduction

Owing to its extraordinary properties, parity-time (PT) symmetry has drawn considerable attention in the physics of non-Hermitian systems since Bender et. al. first discovered in 1998 that non-Hermitian Hamiltonians obeying PT symmetry can possess real energy spectra in quantum mechanics^1,2. In optical systems, PT symmetry can be readily established in a 1D bilayer structure through incorporating gain and loss materials in a judiciously balanced fashion. Such a PT-symmetric photonic system in general can be characterized by a general two-port scattering matrix whose eigenvalues are either unimodular in the PT-symmetric phase or come in inverse-complex-conjugate pairs in PT-broken phase^3,4,5,6. The transition from the PT-symmetric to the PT-broken phase takes place at so-called exceptional points (EPs)^7,8,9,10. During the past decade, an enormous amount of theoretical and experimental work on EPs has stimulated various applications, such as unidirectional invisibility¹¹, non-reciprocal light transmission and energy transfer^12,13, single-mode lasing^14,15, mode switching¹⁶, electromagnetically induced transparency^17,18, as well as enhanced sensing sensitivity enabled by eigenfrequency splitting^19,20,21. In addition to the presence of the symmetry-breaking transition points^22,23,24, the PT-symmetric system also features a self-dual spectral singularity in the regime of broken-PT symmetry, where a pole and a zero of a scattering matrix appearing in a complex conjugate pair in the complex frequency domain coincide at a specific real frequency, called a coherent perfect absorber-laser (CPAL) point. In general, a real-frequency pole (zero) corresponds to an infinite (infinitesimal) eigenvalue, which is associated with the lasing (coherent perfect absorption (CPA)) eigenstate of the scattering matrix³. Thanks to singular characters at the CPAL point, PT-symmetric CPAL systems have been experimentally realized to function as a laser oscillator and as an anti-laser^25,26,27. Experimental implementations of CPAs have also been demonstrated in different fields, including quantum optics²⁸, optical logic gates²⁹, and nonlinear physics³⁰. Although CPA-related theoretical studies on chiral metamaterials^31,32 and refractive index sensing^33,34 were previously reported, the application of PT-symmetry for the detection of chiral substances remains largely unexplored.

Chirality is a fundamental property of life. Sensing the dominant handedness of chiral substances is crucial to numerous scientific subfields of chemistry, biology, and medicine, and to pharmaceutical, cosmetic and food industries. Detecting the inherently weak chiral responses of molecules remains one of the great challenges in the fields of optics and photonics. The poor detection sensitivities of current optical techniques and the difficulties in analyzing the weak signals of substrate-based sensors do not allow important biological and medical processes to be precisely probed and prevent further understanding and treatment of various diseases. Developing highly sensitive chiroptical spectroscopy methods is important because these methods are used to probe the folding of proteins, the yield of enantioselective chemical synthesis and the purity of processed chemicals (i.e., in the pharmaceutical and chemical industries), and to study fundamental optical and physicochemical interactions that can be developed to separate the enantiomers³⁵. Therefore, the photonics community is actively seeking powerful new ways to enhance the chiroptical signals of molecules.

Here we present a chiral sensing mechanism based on the unusual and distinctive eigenbehaviors of the CPA offered by PT-symmetry. In contrast to extracting a faint AC signal from an intense DC signal, typically existing in homodyne measurements^36,37, the PT-symmetric system operating at the CPA mode reveals a self-sustaining null intensity on its output channels with an extraordinarily large extinction depth, which enables us in complete darkness to probe a subtle change in weak chiroptical signals induced by the binding of chiral molecules to the surfaces of the unperturbed PT-symmetric system. Just like you observe a minimum transmitted power or intensity, I_t → 0, as incident light passes through two crossed polarizers commonly used in polarization measurement. If a perturbed object is placed between the crossed polarizers, any polarization effects present in the object, such as birefringence, will cause an increase in transmitted intensity, I_t + ∆I_t. Distinct from the crossed polarizers, the sensitivity of such a CPA-based PT-symmetric system to a small perturbation is in principle infinitely large nearby the CPAL point. In this work, we demonstrate that the chiroptical responses are substantially enhanced at the CPAL point and highly sensitive to molecular chirality, compared to those in the absence of the PT-symmetric substrate, with a potential for the detection of the chirality of monolayers. Besides, the structurally achiral PT-symmetric substrate itself does not contribute to undesired background signals so that absolute measurements of the chirality of molecules become feasible. Our work represents a characteristic example of applying non-Hermitian systems to boost chiroptical responses and could lead to a promising solution for the detection of extremely faint chiroptical signals without the need for complicated fabrication of nanoengineered structures.

Results and discussion

Eigenbehaviors of PT-symmetric system S ^PT

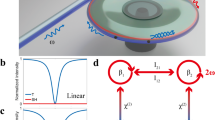
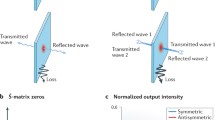
Since chiral molecules only manifest their handedness during their interaction with the chiral state of light (such as circularly-polarized (CP) light), the vectorial electromagnetic waves are represented in terms of the unit circular basis vectors (e_±) and then expressed as in the form of circular Jones vectors (Fig. 1a). The solution to the eigenvalue problem of S^PT yields two degenerate pairs of eigenvalues, s₁ = s₂ and s₃ = s₄, and four corresponding eigenstates, ${\psi }_{i}^{T}=[{a}_{+,i},{d}_{-,i},{a}_{-,i},{d}_{+,i}]$, i = {1,2,3,4}. Because there are two zero elements for each eigenstate, each eigenstate only consists of two counter-propagating CP incident waves of opposite handedness, namely either ${\psi }_{i}^{T}=[{a}_{+,i},{d}_{-,i}]$, i = {1,3} or ${\psi }_{i}^{T}=[{a}_{-,i},{d}_{+,i}]$, i = {2,4} (Supplementary Note 2 for details of s_i and ψ_i). As shown in Fig. 1b, the eigenvalue spectrum of S^PT, the absolute value of the eigenvalues of S^PT as a function of wavelength λ, clearly illustrates two distinct regimes of the PT phase separated by a phase transition point or an EP at which all four eigenvalues coalesce with two degenerate pairs of eigenstates, ψ₁ = ψ₃ and ψ₂ = ψ₄. In the PT-symmetric phase, in spite of s₁ = s₂ ≠ s₃ = s₄, the eigenvalues are unimodular, |s_i| = 1, i = {1,2,3,4}, implying that there is neither net amplification nor net attenuation between output and input states. Their eigenstates satisfy $\hat{P}\hat{T}{\psi }_{i}\propto {\psi }_{j},\left\{i,j\right\}=\left\{{{{{\mathrm{1,2}}}}}\right\},\left\{{{{{\mathrm{2,1}}}}}\right\},\left\{{{{{\mathrm{3,4}}}}}\right\},\left\{{{{{\mathrm{4,3}}}}}\right\}$, indicating that the $\hat{P}\hat{T}$ operator maps one eigenstate into the oppositely handed eigenstate associated with the same eigenvalue. Although each eigenstate is not itself PT-symmetric, a linear combination of two PT-nonsymmetric eigenstates associated with the same eigenvalue is PT-symmetric (i.e., $\hat{P}\hat{T}\left({\psi }_{1}+{\psi }_{2}\right)\propto {\psi }_{1}+{\psi }_{2}$ and $\hat{P}\hat{T}\left({\psi }_{3}+{\psi }_{4}\right)\propto {\psi }_{3}+{\psi }_{4}$). In the PT-broken phase, despite s₁ = s₂ ≠ s₃ = s₄ and |s₁| = |s₂| > 1 > |s₃| = |s₄|, the eigenvalues come in pairs with reciprocal moduli, ${s}_{i}{s}_{j}^{* }=1,\left\{i,j\right\}=\left\{1\;{{{{{\rm{or}}}}}}\;{{{{\mathrm{2,3}}}}}\;{{{{{\rm{or}}}}}}\;4\right\},\left\{3\;{{{{{\rm{or}}}}}}\;{{{{\mathrm{4,1}}}}}\;{{{{{\rm{or}}}}}}\;2\right\}$, meaning that there exists amplification and attenuation between output and input states. Their eigenstates satisfy $\hat{P}\hat{T}{\psi }_{i}={\psi }_{j},\left\{i,j\right\}=\left\{{{{{\mathrm{1,4}}}}}\right\},\left\{{{{{\mathrm{2,3}}}}}\right\},\left\{{{{{\mathrm{3,2}}}}}\right\},\left\{{{{{\mathrm{4,1}}}}}\right\}$, signifying that the $\hat{P}\hat{T}$ operator transforms one eigenstate into the oppositely handed eigenstate associated with different eigenvalue. Similarly, the sum of two PT-nonsymmetric eigenstates with the same eigenvalue fulfills $\hat{P}\hat{T}\left({\psi }_{1}+{\psi }_{2}\right)={\psi }_{3}+{\psi }_{4}$ and $\hat{P}\hat{T}\left({\psi }_{3}+{\psi }_{4}\right)={\psi }_{1}+{\psi }_{2}$, which are not PT-symmetric. Besides, the eigenvalue spectrum of S^PT in the PT-broken phase exhibits a self-dual spectral singularity at a CPAL point whose eigenvalues approach zero and infinity associated with the CPA and lasing eigenstates, respectively (Supplementary Notes 3 and 4 for details of s_i and ψ_i at the EP and the CPAL wavelength).

Fig. 1: Eigen characteristics of PT-symmetric system S^PT.

a PT-symmetric system composed of two homogeneous isotropic gain and loss slabs of equal length (L₃ = L₄ = L) with refractive indices n₃ = 2.1 − 0.207i and n₄ = 2.1 + 0.207i is characterized by a scattering matrix S^PT in circular polarization representation. a, d and b, c represent the complex electric-field amplitudes of normally incident and scattered circularly-polarized (CP) waves propagating along the z axis, respectively. The + (−) sign in the subscript indicates left- and (right-) handed CP [LCP and (RCP)] states, respectively. The geometry is infinite in the x and y directions with water as a background medium (n₁ = n₆ =  1.33). b Semi-log plot of the modulus of the eigenvalues of S^PT as a function of wavelength λ. Green circles denote the coherent perfect absorber-laser (CPAL) point and exceptional point (EP) separates two distinct PT phases. c, d Semi-log plot of the relative amplitude A and phase ϕ of the two counter-propagating oppositely handed CP incident waves of the same wavelength, extracted from the eigenstates of S^PT, as a function of λ. e Semi-log plot of the output coefficient Θ as a function of λ for the lasing-locked, CPA-locked, and eigen S^PT systems. CPA is an acronym for coherent perfect absorption.

In addition, the eigenstates of S^PT display very intriguing and unique properties in different PT phases. The matrix configuration of S^PT implies two independent responses at normal incidence: for input pair of a₊ and d₋, the output state |Ψ_O〉 is a RCP reflected wave b₋ and a LCP transmitted wave c₊, while in response to the oppositely handed input pair of a₋ and d₊, |Ψ_O〉 is a LCP reflected wave b₊ and a RCP transmitted wave c₋. With the incoming CP waves [a_+,i, d_−,i, a_−,i, d_+,i] extracted from each eigenstate ${\psi }_{i}^{T}$, i = {1,2,3,4} associated with the same eigenvalue s_i for different wavelength λ, we obtain the following significant relationships: ${a}_{+,1}/{d}_{-,1}={a}_{-,2}/{d}_{+,2}={A}_{p}{e}^{i{\phi }_{p}}$ and ${a}_{+,3}/{d}_{-,3}={a}_{-,4}/{d}_{+,4}={A}_{q}{e}^{i{\phi }_{q}}$, where A and ϕ, respectively, represent the relative amplitude and phase of the two counter-propagating oppositely handed CP incident eigenwaves of the same wavelength, with the subscript p (q) denoting the associated eigenvalues s₁ = s₂ (s₃ = s₄). The relationships among the relative amplitude A, phase ϕ and wavelength λ in different PT phase domains are illustrated in Fig. 1c, d, respectively, and summarized in Table 1 (Supplementary Note 5).

Table 1 Characteristics of eigenstates of a 4 × 4 S^PT in different phases.

Figure 1d specifies that the phase difference between the two counter-propagating oppositely handed CP incident beams of the same wavelength is exactly π/2 for m = 0 in the PT-broken phase. By fixing their relative phase at π/2, we can achieve coherent switching between the same-handed pair of absorbing and amplifying eigenstates, that is, (ψ₃ ↔ ψ₁) and (ψ₄ ↔ ψ₂), by simply varying the intensity ratio of the two CP incident beams, as indicated in Fig. 1c. The intensity ratios and phase differences of two independent pairs of [a₊, d₋] and [a₋, d₊] beams can be experimentally tuned through adjustments of two separate sets of neutral density filters and optical delay lines. We can locate the wavelength of the CPAL point, λ_CPAL, by sweeping the wavelength of the coherent incident beams while observing a minimum of output coefficient (Θ) defined as $\Theta =({|{b}_{-}+{b}_{+}|}^{2}+{|{c}_{+}+{c}_{-}|}^{2})/({|{a}_{+}+{a}_{-}|}^{2}+{|{d}_{-}+{d}_{+}|}^{2})$. Once the minimum Θ is reached, the settings of the neutral density filters and the optical delay lines remain unchanged, in which the input state |Ψ_I〉 is locked to the CPA eigenstates $\left({\psi }_{i}^{{CPA}}\right)$, called the CPA-locked PT-symmetric system. The switching from the CPA to lasing eigenstates can be readily accomplished by rotating the neutral density filters until Θ goes to maximum. Figure 1e shows how Θ varies with the wavelength of the coherent incident beams for the lasing-locked, CPA-locked, and eigen S^PT systems. Significant linewidth narrowing of the CPA mode at λ_CPAL for CPA-locked S^PT can be attributed to the use of either CPA eigenstates (${\psi }_{3}^{{CPA}}$ and ${\psi }_{4}^{{CPA}}$) as an input state, as compared to the eigen-responses (dotted curves) where the wavelength-dependent eigenstates (ψ_i) are used. The lasing eigen-responses (the red dotted curves) overlap with lasing-locked responses (the red solid curves) no matter whether the S^PT system is locked or not.

Chiroptical responses of CPA-locked S ^C

Now let us consider that a one-nanometer-thick layer of a chiral substance adheres to both surfaces of the PT-symmetric structure (layer 2 and 5 in Fig. 2) as the substrate is immersed in a solution containing chiral molecules. The adsorbed chiral layer has an average refractive index ${n}_{c}=1.33+{10}^{-4}i$ and a variable chirality parameter κ. The relation between the output and input states of the PT-symmetric system in the presence of a chiral substance is given by |Ψ_o〉 = S^C|Ψ_I〉, where |Ψ_I〉 can be expressed as a coherent superposition of the CPA eigenstates of ${S}^{{PT}},|{\Psi }_{I} \rangle =\mathop{\sum}\limits_{i}{C}_{i}{\psi }_{i}^{{CPA}}$. Please refer to Supplementary Notes 6, 7, and 11 for the details of calculations of optical rotation ϑ and ellipticity angle χ. As shown in Fig. 2, we demonstrate the capability to detect chiroptical signals from molecularly thin chiral layers bound to the exterior surfaces of the PT-symmetric structure. For one-nanometer-thick layers of chiral substance with κ = ±10⁻⁵ and ±10⁻⁵i (typical values for the chirality parameter of chiral molecules)^38,39, ϑ (arising from circular birefringence(CB)) and χ (originating from circular dichroism (CD)) are as large as 10 mdeg near λ_CPAL and highly sensitive to the sign of κ. Furthermore, it is feasible to achieve the absolute chirality measurements since such a PT-symmetric system composed of a gain–loss bilayer does not make any contributions to the total chiroptical signals owing to its structurally achiral nature (Supplementary Note 8). As a comparison, the reference chiroptical signals (ϑ^Ref and χ^Ref) contributed by the pure chiral layers of the same thickness in the absence of the PT-symmetric substrate under the identical illumination are as small as 9 μdeg (Supplementary Note 9), thus achieving three orders of magnitude enhancement in the chiroptical responses using the CPA-locked PT-symmetric detection scheme.

Fig. 2: Spectra of chirality-dependent optical rotation ϑ and ellipticity angle χ.

The exterior surfaces of S^PT are decorated with a chiral substance characterized by a chirality parameter κ = κ₂ = κ₅ and an average refractive index n_c = n₂ = n₅ to form S^C system. a, d and b, c represent the complex electric-field amplitudes of normally incident and scattered CP waves propagating along the z axis, respectively. The + (−) sign in the subscript indicates LCP and (RCP) states, respectively. Spectra of optical rotation ϑ and ellipticity angle χ (inset) for the purely real κ = ±10⁻⁵ (left column). Spectra of χ and ϑ (inset) for the purely imaginary κ = ±10⁻⁵i (right column). ϑ and χ are obtained from the CPA-locked S^C system with n_c = 1.33 + 10⁻⁴i and the chiral layer thickness L_c = L₂ = L₅ = 1 nm. CPA is an acronym for coherent perfect absorption.

Specifically, ϑ and χ are related to the difference in refractive index and absorption of LCP and RCP light propagating in a homogeneous isotropic chiral medium, respectively. Therefore, it is unsurprised that ϑ scales linearly with the real part of κ (Re(κ)) while χ is proportional to the imaginary part of κ (Im(κ))^40,41. However, those extremely weak chiroptical signals (~8 μdeg) shown in the insets of Fig. 2 counterintuitively imply that Re(κ) can produce χ and Im(κ) can yield ϑ. Our results are in agreement with recent observations that CD or χ signals depend on both Re(κ) and Im(κ)^39,42,43. In order to investigate the origin of such unexpected contributions, we examine plots of the κ-dependence of ϑ and χ measured at λ_CPAL for different values of Im(n_c), where n_c is the average refractive index of the chiral layers, as shown in Fig. 3. For Im(n_c) = 0, which excludes the nonchiral loss term from contributing to the total signal, the chiroptical signals follow the expected behavior, ϑ ∝ Re(κ) and χ ∝ Im(κ). For Im(n_c) ≠ 0, however, Re(κ) and Im(κ) contribute to a different extent to ϑ and χ. The slopes of χ(Re(κ)) and ϑ(Im(κ)) in the insets of Fig. 3 scale monotonically with Im(n_c), but the change in Im(n_c) has no effect on both ϑ(Re(κ)) and χ(Im(κ)). On the whole, Re(κ) and Im(κ) are dominantly responsible to ϑ and χ, respectively, regardless of Im(n_c) as obviously indicated by overlaid dashed and dotted lines shown in Fig. 3. Consequently, the appearance of the extremely small chiroptical signals shown in the insets of Fig. 2 can be attributed to the consequence of Im(n_c) ≠ 0, and their relative contributions to the overall chiroptical signals are negligibly small and can be ignored (Supplementary Note 10 for purely real n_c case).

Fig. 3: Effect of the nonchiral loss term, Im(n_c), on chirality-dependent optical rotation ϑ and ellipticity angle χ.

a Optical rotation ϑ and ellipticity angle χ (inset) as a function of chirality parameter κ ranging from −5 × 10⁻⁵ to 5 × 10⁻⁵ (purely real κ). b χ and ϑ (inset) as a function of κ ranging from −5 × 10⁻⁵i to 5 × 10⁻⁵i (purely imaginary κ). ϑ and χ are obtained from the CPA-locked S^C with L_c = 1 nm and n_c = 1.33+iIm(n_c), where L_c and n_c are the thickness and average refractive index of the chiral layers, respectively. Different values of Im(n_c) are represented by colors and CPA is an acronym for coherent perfect absorption.

Figure 4a, b show the κ-dependence of ϑ and χ measured at λ_CPAL for different chiral layer thicknesses (L_c). The linear dependence between enhanced ϑ (χ) and the real (imaginary) part of κ indicates that the magnitude and sign of the real (imaginary) part of κ can be quantitatively determined through measurements of far-field chiroptical signals for a given chiral layer thickness, which allows for unambiguous discrimination of the chirality of an unknown sample. As shown in Fig. 4c, d, the sensitivity, expressed as the change in ϑ (χ) with respect to the change in the real and imaginary part of κ, is nearly unaltered for L_c less than 10 nm, even though there is a small variation in the real part of n_c, namely 1.33 + δn_c, which may be caused by fluctuations in temperature and humidity. As L_c gets thicker, the influence of δn_c on the effective refractive index of the overall PT-symmetric system becomes prominent, and the contribution of the refractive index perturbation to the system’s sensitivity might need to be taken into consideration. Once again, for those relatively weak chiroptical shown in the insets of Fig. 4, their emergence can be attributed to the consequence of the presence of Im(n_c) and their relative contributions to the total chiroptical signals are negligible for thinner L_c. The CPA-locked PT-symmetric detection scheme allows for quantitative detection of the chirality parameter κ of the adsorbed chiral substance even though there exists a nonchiral loss term in its refractive index. We have to emphasize that our analytical model is valid only when the unperturbed CPA-locked S^PT is exposed to a small perturbation (such as a small κ and δn_c with a comparable thin chiral layer). As the external perturbation becomes larger, the perturbed system S^C will not be able to hold the eigenstates of the unperturbed system S^PT. Moreover, even though κ is assumed independent of wavelength over a specified wavelength range, it is still possible to probe the chiroptical activity of an optically active sample as long as the sample to be detected has a finite-valued κ nearby λ_CPAL. This gives us a great opportunity to explore vibrational optical activity outside the ultraviolet wavelength region in which the optical rotatory dispersion and electronic CD measurements are usually carried out⁴⁴.

Fig. 4: Sensitivity of chirality-dependent optical rotation ϑ and ellipticity angle χ for different chiral layer thicknesses.

a Optical rotation ϑ and ellipticity angle χ (inset) as a function of chirality parameter κ ranging from −5 × 10⁻⁵ to 5 × 10⁻⁵ (purely real κ). b χ and ϑ (inset) as a function of κ ranging from −5 × 10⁻⁵i to 5 × 10⁻⁵i (purely imaginary κ). ϑ and χ are obtained from the CPA-locked S^C with the average refractive index of the chiral layers, n_c = 1.33 + 10⁻⁴i. c ∆ϑ/∆Re(κ) and ∆χ/∆Re(κ) (inset) and d ∆χ/∆Im(κ) and ∆ϑ/∆Im(κ) (inset) as a function of refractive index perturbation δn_c ranging from −5 × 10⁻⁴ to 5 × 10⁻⁴ for the CPA-locked S^C with n_c = (1.33 + δn_c) + 10⁻⁴i. Different values of chiral layer thickness L_c are represented by colors. KU stands for the unit of κ and CPA is an acronym for coherent perfect absorption.

Spatially dependent differential absorption

To further understand the underlying mechanism of how the CPA-locked S^C enhances chiroptical signals, especially CD, we first investigate the optical absorption of two independent pairs of internal $[{c}_{+}^{j},{d}_{-}^{j}]$ and $[{c}_{-}^{j},{d}_{+}^{j}]$ beams in response to their respective input states, $[{a}_{+}^{1},{d}_{-}^{6}]={\psi }_{3}^{{CPA}}$ and $[{a}_{-}^{1},{d}_{+}^{6}]={\psi }_{4}^{{CPA}}$, as schematically illustrated in Fig. 5. Based upon the time-averaged power densities evaluated at the initial position z₂ and at a relative position z' (0 ≤ z' ≤ L_j) inside the layer j with a length of L_j, j = {2,3,4,5}, we are capable of examining how the differential absorption evolves internally as the internal $[{c}_{+}^{j},{d}_{-}^{j}]$ and $[{c}_{-}^{j},{d}_{+}^{j}]$ beams propagate through the successive layers⁴⁵. Please refer to Supplementary Note 12 for detailed derivations of expressions.

Fig. 5: Spatially dependent differential absorption ∆α(z) of two independent pairs of internal $\left[{c}_{+}^{j},{d}_{-}^{j}\right]$ and $\left[{c}_{-}^{j},{d}_{+}^{j}\right]$ beams.

The profile of ∆α(z) as a function of the propagation distance z for three different cases of chiral absorption κ = 0 and κ =  ± 10⁻⁵i, obtained from the CPA-locked S^C with refractive indices n₃ = 2.1 − 0.207i and n₄ = 2.1 + 0.207i (a) and from the pure chiral layers of the same thickness in the absence of the PT-symmetric substrate with refractive indices n₃ = n₄ = n₁ = n₆ = 1.33 (b). $\left[{a}_{+}^{1},{d}_{-}^{6}\right]$ and $\left[{a}_{-}^{1},{d}_{+}^{6}\right]$ are the coherent perfect absorption (CPA) eigenstates of S^PT and serve as the inputs of the system while $\left[{c}_{+}^{6},{b}_{-}^{1}\right]$ and $\left[{c}_{-}^{6},{b}_{+}^{1}\right]$ are the corresponding responses, where the + (−) sign in the subscript indicates LCP and (RCP) states. $\left[{c}_{+}^{j},{d}_{-}^{j}\right]$ and $\left[{c}_{-}^{j},{d}_{+}^{j}\right]$ denote the complex electric-field amplitudes of counter-propagating oppositely handed internal beams at the interface z_j inside the layer j with a thickness of L_j = z_j+1 − z_j, j = {2,3,4,5}. For visibility, the chiral layer with a thickness of L_c = L₂ = L₅ = 50 nm and an average refractive index of n_c = 1.33 + 10⁻⁴i is chosen and represented by gray shaded areas. Chirality-dependent ∆α(z₆) is denoted by blue downward and red upward arrows.

Figure 5a depicts the differential absorption of $[{c}_{-}^{j},{d}_{+}^{j}]$ and $[{c}_{+}^{j},{d}_{-}^{j}]$ beams, defined as ∆α(z), as a function of the propagation distance z for the CPA-locked S^C with 50-nm-thick chiral layers. ∆α(z) is computed at λ_CPAL for three different cases of chiral absorption, κ = 0 and κ = ±10⁻⁵i. For Im(κ) = 0, the absorption of $[{c}_{-}^{j},{d}_{+}^{j}]$ at any z is completely identical to that of $[{c}_{+}^{j},{d}_{-}^{j}]$ at the same position, thus resulting in ∆α(z) = 0, irrespective of the presence of the balanced gain and loss in the CPA-locked PT-symmetric system. In the presence of chiral absorption (Im(κ) ≠ 0), we observe chirality-dependent ∆α(z) and dissymmetry in the spatial profiles of ∆α(z) with respect to the center of PT-symmetric structure, with ripples caused by the differential interference of $[{c}_{-}^{j},{d}_{+}^{j}]$ and $[{c}_{+}^{j},{d}_{-}^{j}]$ beams. In fact, the differential transmitted intensity in layer 6 $({|{c}_{+}^{6}|}^{2}-{|{c}_{-}^{6}|}^{2})$ that scales with the CD signal (Supplementary equation (23)) is proportional to the differential absorption at the position z₆, ∆α(z₆). As shown in Fig. 5a, the signs of the chirality-dependent ∆α(z₆), denoted by blue downward and red upward arrows corresponding respectively to Im(κ) >0 and Im(κ) <0, are in accord with those of the calculated χ shown in Fig. 2. The magnitudes of the chirality-dependent ∆α(z₆) get considerably increased by a factor of up to ~10³ compared to those of the reference differential absorption (∆α(z₆)^Ref) from the pure chiral layers of the same thickness in the absence of the PT-symmetric substrate under the identical illumination shown in Fig. 5b, which are consistent with the aforementioned enhancement of three orders of magnitude in the chiroptical responses (Fig. 2 and Supplementary Fig. S2).

An ultrasensitive monochromatic chiroptical sensor

We now consider the responses of the CPA-locked S^C with L_c = 50 nm to complex-valued κ. Figure 6 illustrates the polarization ellipses of the time-dependent transmitted beams (c₊e₊ + c₋e₋) at λ_CPAL for four possible combinations of the complex-valued κ. The results show that a positive value of Re(κ) contributes to a negative ϑ, while a positive value of Im(κ) leads to a negative χ. For purely real n_c = 1.33 with the specified values of κ given in Fig. 6, we obtain symmetric distributions of (ϑ, χ) = (±0.532°, ±0.532°), whereas (ϑ,χ) for n_c = 1.33 + 10⁻⁴i are equal to (0.509°, 0.553°), (−0.553°, 0.509°), (−0.509°, −0.553°), and (0.553°, −0.509°). This asymmetry is because there exists a lossy term in the nonchiral part of the sample’s refractive index (n_±) and the differences between the results of two different cases of n_c are all less than ±5%. Potentially being an ultrasensitive monochromatic chiroptical sensor, the CPA-locked S^C reveals the enhanced chiroptical signals of ~±0.5° merely from two 50-nm-thick chiral layers adhering to the PT-symmetric surfaces, which are well above the sensitivity range of the commercial CB and CD instruments that commonly have an accuracy of 1 mdeg. In general, the chiroptical enhancement at λ_CPAL is mediated by the extinction depth of the CPA mode which in principle can be extremely high through fine-tuning the refractive indices of the gain and loss slabs to exactly match the CPA eigensolution³. However, the overall performance of the PT-symmetric system is practically limited by noises, such as photon shot noise level nearby λ_CPAL as well as flicker noise and amplitude/phase noise from the detectors and laser sources used in the measurements^34,46.

Fig. 6: Circular basis representation of the elliptically polarized transmitted beam (c₊e₊ + c₋e₋).

Four possible combinations of the complex-valued chirality parameter κ are considered and the results are shown in four different quadrants in the plane of optical rotation ϑ and ellipticity angle χ. The radius of the red (blue) dotted circle denotes the absolute value of the complex transmitted wave c₊ (c₋) expressed in terms of the unit circular basis vectors e₊ (e₋), where the + (−) sign in the subscript indicates LCP and (RCP) states, respectively. The angle between the positive x-axis and the red (blue) colored arrow that represents the electric-field vector c₊e₊ (c₋e₋) at time t = 0 signifies the initial phase of c₊ (c₋). The red and blue colored arrows rotate in the counterclockwise (LCP) and clockwise (RCP) direction, respectively, as the beam propagates along the positive z direction. The superposition of c₊e₊ and c₋e₋ generates an elliptically polarized light (green dotted ellipse) and the direction of rotation of the green-colored arrow is the same as that of the circular component with a larger radius. For visibility purposes, the green dotted ellipses are redrawn with an aspect ratio of 1:10 (x:y) shown at the bottom of each panel. (Supplementary Note 13 and Supplementary Movie 1 for details).

Undoubtedly, any slight relative changes on the refractive index and thickness of the gain–loss bilayer, mainly caused by imperfections during the sensor manufacturing process, will significantly affect the chiroptical responses (${\vartheta }^{{S}^{C}}$ and ${\chi }^{{S}^{C}}$). The former ${n}_{3}\ne {n}_{4}^{* }$ can be alleviated with the bilayer structure made by low refractive index materials, for instance, Re[n] = 1.5, and considerably improved by allowing refractive index and dispersion accurate to the fourth decimal place or better. As for the latter L₃ ≠ L₄, the thin slab of micrometer size imposes a constraint that requires a thickness precision of sub-nm, which can be achieved by atomic layer deposition given that the dielectric material is chosen as the gain–loss material. With these requirements, one can have a decent CPA mode, while maintaining at least 50% of maximal chiroptical signals of the ideally PT-symmetric system.

Conclusions

In summary, we have demonstrated that the CPA-locked PT-symmetric system is capable of, in a highly sensitive manner, boosting chirality-dependent signals from molecularly thin chiral layers bound to the surfaces of the PT-symmetric substrate. The structurally achiral PT-symmetric system itself does not make any contributions to the total chiroptical signals, which enables absolute chirality measurements without requiring the background subtraction and the substrate removal for acquiring a reference measurement. A 1000-fold enhancement in the chiroptical responses offered by the CPA-locked PT-symmetric system makes it feasible to sense the molecular chirality of monolayered substances with existing research-grade instruments, which was previously unattainable. The linear dependence between enhanced ϑ (χ) signals and Re(κ) (Im(κ)) allows for quantitative and unambiguous discrimination of the chirality of an unknown sample even though there exists a lossy term in the nonchiral part of the sample’s refractive index. Furthermore, we develop an analytical model to provide an insightful interpretation of physical mechanisms behind chiroptical enhancements supported by the CPA-locked PT-symmetric system. The CPA-locked PT-symmetric detection scheme has not been studied before and may be regarded as a promising chiral-sensitive platform for detections of extremely small chiral biomolecules, monolayers of chiral substances, and self-assembled chiral layers with high sensitivity. Our study explores the fundamental properties of non-Hermitian chiral photonics and paves the way for ultrasensitive chiroptical sensors and their applications.

Methods

Transfer matrix in circular polarization representation

Transfer matrix formalism is used to analyze the propagation of electromagnetic waves through a PT-symmetric system in the absence and presence of chiral layers present in mediums 2 and 5, respectively. Because there are two possible circular polarizations (left-handed circular polarization, LCP (+), and right-handed circular polarization, RCP (−)) for the forward- and back-propagating waves on each of two sides of the system, the PT-symmetric system can be described by a 4 × 4 transfer matrix M which relates a 4 × 1 circular Jones vector on the one side to the other 4 × 1 circular Jones vector on the opposite side, as illustrated by the green arrows in medium 1 and 6 of Fig. 1a.

$$\left[\begin{array}{c}{a}_{+}\\ \begin{array}{c}{a}_{-}\\ {b}_{+}\\ {b}_{-}\end{array}\end{array}\right]=M\left[\begin{array}{c}{c}_{+}\\ \begin{array}{c}{c}_{-}\\ {d}_{+}\\ {d}_{-}\end{array}\end{array}\right],M=\left\{\begin{array}{c}\begin{array}{c}{T}_{13}\,{P}_{3}\,{T}_{34}\,{P}_{4}\,{T}_{46}={M}^{{PT}},{{{{{\rm{without}}}}}}\; {{{{{\rm{chiral}}}}}}\; {{{{{\rm{layers}}}}}}\hfill\\ {T}_{12}\,{P}_{2}\,{T}_{23}\,{P}_{3}\,{T}_{34}\,{P}_{4}\,{T}_{45}\,{P}_{5}\,{T}_{56}={M}^{C},{{{{{\rm{with}}}}}}\; {{{{{\rm{chiral}}}}}}\; {{{{{\rm{layers}}}}}}\end{array}\end{array}\right.$$

(1)

where T_ij is a 4 × 4 interface transition matrix from medium i toward medium j, which relates the circular Jones vector ${\left[{a}_{+},{a}_{-},{b}_{+},{b}_{-}\right]}_{i}^{T}$ on the left-hand side to the other ${\left[{c}_{+},{c}_{-},{d}_{+},{d}_{-}\right]}_{j}^{T}$ on the right-hand side of the interface, with the superscript T indicating transpose, P_j is a 4 × 4 propagation matrix that accounts for the phase contributed by forward- and backward-CP waves propagating inside the medium j with a thickness of L_j, and M is a 4 × 4 global transfer matrix obtained by successive multiplication of individual T_ij and P_j matrices. The number of rows of the transfer matrix corresponds to four independent boundary conditions at the interface, i.e., the continuity of tangential electric and magnetic fields. The transfer matrix method explicitly takes into consideration the effect of multiple reflection and transmission of light at all interfaces on the overall system responses.

Bi-isotropic constitutive relations and eigenmodes in chiral medium

Chiral medium, present in layers 2 and 5, is a bi-isotropic medium, in which complex electric and magnetic flux densities (D and B) and fields (E and H) are related by the bi-isotropic constitutive relations which can be written in the time-harmonic convention e^−iωt as D = ε₀ε_rE + i(κ/c) H and B = μ₀μ_rH − i(κ/c) E, where ε₀ and μ₀ are the permittivity and permeability of free space, ε_r and μ_r are the relative permittivity and permeability of the chiral layer, c is the speed of light in free space, and κ is the chirality parameter of the chiral substance. κ measures the degree of the handedness of the material and a change in the sign of κ means taking the mirror image of the material⁴⁷. The eigenmodes propagating along the z axis in the chiral region can be found by inserting the constitutive relations into time-harmonic Maxwell equations, ∇ × E = iωB and ∇ × H = −iωD, in a matrix formulation, whereby the matrix is represented in terms of its eigenvalues k_± = k₀n_± = k₀(n_j ± κ_j) & = −k₀(n_j ± κ_j), the wavenumbers of the medium for the LCP (+) and RCP (−) waves propagating along the positive and negative z axis, and its associated eigenvectors ${{{{{{\boldsymbol{e}}}}}}}_{{\pm }}=\left(\hat{{{{{{\boldsymbol{x}}}}}}}\pm i\hat{{{{{{\boldsymbol{y}}}}}}}\right)/\sqrt{2}\& =\left(-\hat{{{{{{\boldsymbol{x}}}}}}}\pm i\hat{{{{{{\boldsymbol{y}}}}}}}\right)/\sqrt{2}$, unit column vectors that play the role of the circular basis for the LCP (+) and RCP (−) electric field, where n_j and κ_j denote the average refractive index and the chirality parameter of the medium j, respectively. The relation between magnetic and electric unit vectors is given by h_± = ∓ie_±. Therefore, the allowed solutions of the plane waves for the chiral medium are four distinct eigenmodes (${{{{{{\bf{E}}}}}}}_{\pm }\left(z\right)=E{{{{{{\boldsymbol{e}}}}}}}_{\pm }{e}^{i{k}_{\pm }z}\& =E{{{{{{\boldsymbol{e}}}}}}}_{\pm }{e}^{-i{k}_{\pm }z}$, ${{{{{{\bf{H}}}}}}}_{\pm }\left(z\right)=E{\eta }_{\pm }^{-1}{{{{{{\boldsymbol{h}}}}}}}_{\pm }{e}^{i{k}_{\pm }z}\& =E{\eta }_{\pm }^{-1}{{{{{{\boldsymbol{h}}}}}}}_{\pm }{e}^{-i{k}_{\pm }z}$ with the complex electric-field amplitude E) propagating along the z axis with different phase velocities (v_± = c/(n_j ± κ_j)), where η_± = η₀/n_j is the impedance parameters of the medium j with η₀ being the characteristic impedance of free space. It should be noted that the impedance parameters do not depend on the chirality parameter while the wavenumbers do. The aforementioned equations hold for the fields in nonchiral medium (i.e., layer 1, 3, 4, and 6) with κ = 0.

Scattering matrix in circular polarization representation

Scattering matrices, S^PT and S^C, connect the output state |Ψ_O〉 = [b₋,c₊,b₊,c₋]^T, the complex electric-field amplitudes of the outgoing CP waves, to the input state |Ψ_I〉 = [a₊,d₋,a₋,d₊]^T, those of the incoming CP waves, represented by the arrows in medium 1 and 6 of Fig. 1, respectively^6,32. In general, the scattering matrix S^PT and S^C can be constructed from the transfer matrix M^PT and M^C, respectively (Supplementary Note 1).

$$\left[\begin{array}{c}{b}_{-}\\ \begin{array}{c}{c}_{+}\\ {b}_{+}\\ {c}_{-}\end{array}\end{array}\right]= \,S\left[\begin{array}{c}{a}_{+}\\ \begin{array}{c}{d}_{-}\\ {a}_{-}\\ {d}_{+}\end{array}\end{array}\right]=\left[\begin{array}{cccc}{r}_{-+}^{L} & {t}_{--}^{R} & {r}_{--}^{L} & {t}_{-+}^{R}\\ {t}_{++}^{L} & {r}_{+-}^{R} & {t}_{+-}^{L} & {r}_{++}^{R}\\ {r}_{++}^{L} & {t}_{+-}^{R} & {r}_{+-}^{L} & {t}_{++}^{R}\\ {t}_{-+}^{L} & {r}_{--}^{R} & {t}_{--}^{L} & {r}_{-+}^{R}\end{array}\right]\left[\begin{array}{c}{a}_{+}\\ \begin{array}{c}{d}_{-}\\ {a}_{-}\\ {d}_{+}\end{array}\end{array}\right],\\ {S}= \,\left\{\begin{array}{c}\left[\begin{array}{cccc}{r}^{L} & t & 0 & 0\\ t & {r}^{R} & 0 & 0\\ 0 & 0 & {r}^{L} & t\\ 0 & 0 & t & {r}^{R}\end{array}\right]={S}^{{PT}},{{{{{\rm{without}}}}}}\; {{{{{\rm{chiral}}}}}}\; {{{{{\rm{layers}}}}}}\\ \left[\begin{array}{cccc}{r}_{-+}^{L} & {t}_{--}^{R} & 0 & 0\\ {t}_{++}^{L} & {r}_{+-}^{R} & 0 & 0\\ 0 & 0 & {r}_{+-}^{L} & {t}_{++}^{R}\\ 0 & 0 & {t}_{--}^{L} & {r}_{-+}^{R}\end{array}\right]={S}^{C},{{{{{\rm{with}}}}}}\; {{{{{\rm{chiral}}}}}}\; {{{{{\rm{layers}}}}}}\end{array}\right.$$

(2)

where r and t are complex amplitude reflection and transmission coefficients, the superscript L and R indicate the incoming CP waves on the left- or right-handed sides of the system, and the first and second subscripts denote the handedness of the scattered and incident CP waves, respectively. Unlike the transfer matrix, each matrix element of the scatting matrix has its physical meaning. In the case of S^PT, eight of off-diagonal elements are zero, ${r}_{--}^{L}={t}_{-+}^{R}={t}_{+-}^{L}={r}_{++}^{R}=0$ and ${r}_{++}^{L}={t}_{+-}^{R}={t}_{-+}^{L}={r}_{--}^{R}=0$, because of the conditions of continuity at the interfaces, and the rest of off-diagonal elements are nonzero and equal, ${t}_{--}^{R}={t}_{++}^{R}={t}_{++}^{L}={t}_{--}^{L}\equiv t$, owing to the conservation of energy and time-reversal symmetry. Four diagonal elements can be reduced to two, ${r}_{-+}^{L}={r}_{+-}^{L}\equiv {r}^{L}$ and ${r}_{+-}^{R}={r}_{-+}^{R}\equiv {r}^{R}$, irrespective of the handedness of the incident waves. It is apparent that S^PT is a non-Hermitian matrix, ${S}^{{PT}}\,\ne\, {{S}^{{PT}}}^{{{\dagger}} }$, where the superscript dagger indicates the Hermitian adjoint. Because of respecting PT symmetry, S^PT can be characterized by the invariance ${\sigma }_{x}{\left[{\left({S}^{{PT}}\right)}^{-1}\right]}^{* }{\sigma }_{x}={S}^{{PT}}$ and satisfies the relation $\hat{P}\hat{T}{S}^{{PT}}\hat{P}\hat{T}={\left({S}^{{PT}}\right)}^{-1}$, where the asterisk denotes complex conjugate, $\hat{P}$ is the parity operator ($\hat{P}\equiv {\sigma }_{x}$, the x component of 4 × 4 Pauli matrices) and $\hat{T}$ is the time-reversal operator ($\hat{T}\equiv K$, the complex conjugation operator)^48,49. The resultant S^PT matrix is verified by COMSOL Multiphysics (Supplementary Note 14).