Dissipation-driven strange metal behavior

Abstract

Anomalous metallic properties are often observed in the proximity of quantum critical points, with violation of the Fermi Liquid paradigm. We propose a scenario where, near the quantum critical point, dynamical fluctuations of the order parameter with finite correlation length mediate a nearly isotropic scattering among the quasiparticles over the entire Fermi surface. This scattering produces a strange metallic behavior, which is extended to the lowest temperatures by an increase of the damping of the fluctuations. We phenomenologically identify one single parameter ruling this increasing damping when the temperature decreases, accounting for both the linear-in-temperature resistivity and the seemingly divergent specific heat observed, e.g., in high-temperature superconducting cuprates and some heavy-fermion metals.

Introduction

Landau’s Fermi liquid (FL) theory is one of the most successful paradigms in condensed matter physics and usually describes very well the prominent properties of metals even when the interaction is strong, like, e.g., in heavy-fermion metals or in the normal (non-superfluid) phase of ³He. However, in the last decades, a wealth of systems violating the paradigmatic behavior has been discovered. In particular, it has been noticed that in several different materials, like heavy fermions metals¹, iron-based superconductors², organic metals like (TMTSF)₂PF₆, high-temperature superconducting cuprates (for an extended analysis of several materials see refs. ^3,4), a non-FL behavior can occur in the proximity of quantum critical points (QCPs), i.e., near zero-temperature second-order phase transitions, where the uniform metallic state is unstable towards some ordered state. It is worth mentioning that, apart from the paradigmatic case of the one-dimensional Luttinger liquid, there are also theories for the violation of the FL behavior that do not rely on an underlying criticality^5,6. In some cases, like in high-temperature superconducting cuprates (henceforth, cuprates), the ordered state may be unaccomplished due to disorder, low dimensionality, and/or competition with other phases, like superconductivity. Nevertheless, the non-FL behavior is observed also in these cases of missed quantum criticality, showing that a mere tendency to order and the presence of abundant order parameter fluctuations (henceforth, fluctuations) may be sufficient to create a non-FL state. The general underlying idea is that the fluctuations are intrinsically dynamical, with a characteristic energy m becoming smaller and smaller as the correlation length ξ grows larger and larger, when the QCP is approached. In the paradigmatic case of a Gaussian QCP in a metal, with a dynamical critical index z = 2, the retarded propagator of the fluctuations with wavevector q and frequency ω is^7,8,9,10

$$D({{{{{{{\bf{q}}}}}}}},\omega )={\left(m+\bar{\nu }| {{{{{{{\bf{q}}}}}}}}-{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{c}}}}}}}}}{| }^{2}-{\omega }^{2}/\overline{{{\Omega }}}-{{{{{{{\rm{i}}}}}}}}\gamma \omega \right)}^{-1},$$

(1)

where $m=\bar{\nu }{\xi }^{-2}$ is the mass of the fluctuations, $\bar{\nu }$ is typically an electron energy scale [we work with dimensionless momenta, measured in reciprocal lattice units (r.l.u.) 2π/a], q_c is the critical wavevector, and $\overline{{{\Omega }}}$ is a frequency cutoff. A crucial role in the following will be played by the imaginary term in the denominator, which describes the Landau damping of the fluctuations, as they decay in particle-hole pairs. The dimensionless parameter γ is usually proportional to the electron density of states, which sets a measure of the phase space available for the decay of the fluctuations. It is worthwhile mentioning that the strong correlations of the metal are customarily encoded in a renormalization of the quasiparticle mass and of the effective residual interaction, e.g., within a slave-boson approach^10,11,12. Once these effects are taken into account, a random-phase approximation within the renormalized FL works well to describe the instabilities of the FL, e.g., towards a charge-ordered state, which is a well-established tendency of cuprates, where a wealth of nearly critical and less critical fluctuations have been experimentally detected¹³. Of course, other modes like plasmons and paramagnons mark the spectra of these systems at high energies (some hundreds of meV), where correlation effects surely play a substantial role^14,15, but here we are mostly interested in the low-energy physics of transport phenomena. In this regime the fermionic quasiparticles mostly interact with low-energy collective excitations with a slow overdamped dynamics mostly determined by the proximity to (more or less hidden) instabilities. In two dimensions and for a dynamical critical index z = 2 (as appropriate to Landau-damped collective modes) these low-energy modes are well described by the Gaussian form of the fluctuation propagator reported in Eq. (1). Clearly, in the Gaussian case, for ω = 0 and q ≈ q_c one obtains the standard Ornstein–Zernike form of the static susceptibility. The same behavior of the fluctuations can be obtained within a time-dependent Landau–Ginzburg approach, where γ is the coefficient of the time derivative and the decay rate of the fluctuations is given by ${\tau }_{{{{{{{{\bf{q}}}}}}}}}^{-1}=(m+\bar{\nu }| {{{{{{{\bf{q}}}}}}}}-{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{c}}}}}}}}}{| }^{2})/\gamma$.

Approaching the QCP, ξ grows, m decreases and the fluctuations become softer and softer, thereby mediating a stronger and stronger interaction between the fermion quasiparticles (henceforth, simply quasiparticles). In two and three dimensions the interaction could be strong enough to destroy the FL state¹⁶. For ordering at finite wavevectors, though, there is a pitfall in this scheme¹⁷: due to momentum conservation, this singular low-energy scattering only occurs between quasiparticles near points of the Fermi surface that are connected by q ~ q_c (hot spots). All other regions are essentially unaffected by this singular scattering and most of the quasiparticles keep their standard FL properties. As a result, for instance, in transport, a standard FL behavior would occur, with a T² FL-like resistivity¹⁷. Disorder may help to blur and enlarge the hot regions¹⁸, but it does not completely solve the above difficulty. Of course, this limitation does not occur in cases where q_c = 0 (like, e.g, near a ferromagnetic¹⁹, or a circulating-current²⁰, or a nematic²¹ QCP), or near a local QCP (i.e., when the singular behavior persists locally for all q)^22,23,24,25. However, the very fact that similar non-FL behavior also occurs near QCPs with finite q_c calls for a revision of the above scheme searching for a general and robust way to account for non-FL phases irrespective of the ordering wavevector.

The main goal of the present work is to describe an alternative scenario for the non-FL behavior, based on the idea that the decay rate of the fluctuations ${\tau }_{{{{{{{{\bf{q}}}}}}}}}^{-1}$ becomes very small not only at q ≈ q_c, because of a diverging ξ, but rather at all q’s, because of a (nearly) diverging γ, as T goes to zero at special values of the control parameter as, e.g., doping in cuprates. We will adopt a phenomenological approach and we will explicitly show that a finite ξ and a large γ are generic sufficient conditions to obtain the most prominent signatures of non-FL strange-metal behavior: a linear-in-temperature (T) resistivity (even down to very low temperature) and a (seemingly) diverging specific heat. For the sake of concreteness, we will consider the paradigmatic case of cuprates, where at some specific doping both features are observed^3,26, having in mind that they also commonly occur in many other systems like, e.g. heavy fermions¹. This suggests that our proposal might have a broad applicability.

Results and discussion

Dissipation-driven strange metal behavior

The above scenario can be achieved on the basis of three simple and related ingredients: (a) The proximity to a QCP, bringing the fluctuations to sufficiently low energy; (b) Some quenching mechanism preventing the full development of criticality so that the mass m and the other parameters of the dynamical fluctuations do not vary in a significant way with temperature; (c) Some mechanism driving an increase of the Landau damping parameter γ. Indeed the non-FL behavior persists down to a temperature scale ${T}_{{{{{{{{\rm{FL}}}}}}}}} \sim {\omega }_{0}\equiv m/\gamma =\bar{\nu }/({\xi }^{2}\gamma )={\tau }_{{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{c}}}}}}}}}}^{-1}$ when ξ is finite and not particularly large. In cuprates, recent resonant X-ray scattering (RXS) experiments¹³ show that conditions (a) and (b) hold: the occurrence of a temperature dependent narrow peak due to charge density waves testifies the proximity to a QCP (although hidden and not fully attained due to the competition with the superconducting phase). The concomitant occurrence of broad peak witnesses for the presence of dynamical charge density fluctuations (CDFs) with rather short correlation length and broad momentum distribution. These abundant CDFs are available to isotropically scatter the quasiparticles over a broad range of momenta and no clear distinction can be done between hot and cold Fermi surface regions²⁷. This was the first explicit example that a quenched criticality with a finite ordering wavevector q_c can still give rise to strong but isotropic scattering, thereby bypassing the problem that in standard hot spot models most electrons contribute with a ~ T² scattering rate to transport¹⁷. This shows that conditions (a) and (b) are enough to account for a linear-in-T resistivity above T_FL. Condition (c) becomes instead mandatory because an increasing γ is needed to extend to lower temperatures the non-FL behavior, accounting for the persistence of the linear resistivity observed down to a few Kelvins, which is the so-called strange-metal behavior, sometimes also referred to as the Planckian behavior^3,28 (for a distinction between the strange-metal and the Planckian behavior, see below), as well as a seemingly diverging specific heat^26,29 (see below).

To address this issue, we investigate the effects of an increasing γ on the fluctuations, which provide both a broad scattering mechanism for resistivity and low-energy excitations for the specific heat. From the retarded propagator we obtain the spectral density of the fluctuations^11,30,31,32

$${{{{{{{\rm{Im}}}}}}}}\ D({{{{{{{\bf{q}}}}}}}},\omega )=\frac{\gamma \omega }{{\left(m+\bar{\nu }| {{{{{{{\bf{q}}}}}}}}-{{{{{{{{\bf{q}}}}}}}}}_{{{{{{{{\rm{c}}}}}}}}}{| }^{2}-{\omega }^{2}/\overline{{{\Omega }}}\right)}^{2}+{\gamma }^{2}{\omega }^{2}},$$

which, for q = q_c, is maximum at ω ≈ ω₀ ≡ m/γ. For large γ (whatever the reason), ω₀ is much smaller than m and sets the characteristic energy scale of the dynamical fluctuations. As mentioned above, a large γ suppresses the energy scales associated with ${\tau }_{{{{{{{{\bf{q}}}}}}}}}^{-1}$ at all q’s [One could even argue that when this slow dynamics of the small droplets of the fluctuations (of order ξ) is reached, a kind of almost persistent glassy state is likely formed].

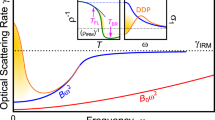
Figure 1 (a) and (b) display this shift to lower frequencies of $b(\omega )\ {{{{{{{\rm{Im}}}}}}}}\ D(\omega )$ and ${{{{{{{\rm{Im}}}}}}}}\ D(\omega )$ when γ increases [$b(\omega )={({{{{{{{{\rm{e}}}}}}}}}^{\omega /T}-1)}^{-1}$ being the Bose function]. Panel (c) schematically shows the corresponding extension of the linear resistivity down to lower and lower temperatures. Indeed, although the collective fluctuations obey the Bose statistics, at any temperature T > ω₀ they acquire a semiclassical character and their thermal Bose distribution becomes linear in T, b(ω) ≈ T/ω. Notice that this is the usual situation for phonons when T is above their Debye temperature. The only difference here is that a small/moderate m (due to the proximity to a QCP) and the large γ conspire to render the Debye scale of the fluctuations particularly small or even vanishing if γ may diverge, while m stays finite. Notice also that the integrated weight of the thermally excited fluctuations, $\int {{{{{{{\rm{d}}}}}}}}\omega \ b(\omega )\ {{{{{{{\rm{Im}}}}}}}}\ D(\omega )$, depends only very weakly on γ.

Fig. 1: Implications of the γ parameter.

Sketch of the shift induced by an increasing damping parameter γ = 1 → 30 on the fluctuation spectral function ${{{{{{{\rm{Im}}}}}}}}\ D$ in the presence (a) and in the absence (b) of a Bose thermal distribution; (c) sketch of the effect on the resistivity induced by the decrease of the characteristic energy ω₀ ≡ m/γ (with m = 10 meV) of the fluctuations responsible for the quasiparticle scattering, with the scattering rate given by the imaginary part of the electron self-energy, computed at second order in the coupling g between electron quasiparticles and fluctuations. The orange dotted line represents the Planckian limit (linearity down to T = 0), corresponding to a divergent γ.

Resistivity in cuprates

In Fig. 2 we report the experimental data for Nd-La_2−xSr_xCuO₄ and Eu-La_2−xSr_xCuO₄ samples with x = 0.24 (from ref. ²⁶, the error bars of the data are smaller than the symbol size), and the resistivity calculated by solving the Boltzmann equation. The scattering rate was obtained from the imaginary part of the electron self-energy, computed at second order in the coupling g between electron quasiparticles and CDFs of the form given by Eq. (1). Details are given in the “Methods” section and in ref. ²⁷.

Fig. 2: Linear-in-T resistivity.

Resistivity calculations for a Nd-La_2−xSr_xCuO₄ sample with x = 0.24 (black solid line) and for a Eu-La_2−xSr_xCuO₄ sample with x = 0.24 (black dashed line). The symbols refer to the experimental data extracted from ref. ²⁶ (the error bars of the data are smaller than the symbol size): filled circles for Nd-La_2−xSr_xCuO₄ and empty squares for Eu–La_2−xSr_xCuO₄. For the fitting we used a quasiparticle-charge fluctuations coupling and the elastic scattering rate due to quenched disorder g² = 0.045 and Γ₀ = 13.7 meV for Nd–La_2−xSr_xCuO₄ and g² = 0.0415 and Γ₀ = 12.3 meV for Eu–La_2−xSr_xCuO₄ (see Methods—the Boltzmann equation and calculation of the electron scattering rate).

This calculation follows closely the approach used in ref. ²⁷ for the fermion tight-binding dispersion, the calculation of the electron scattering rate, and the solution of the Boltzmann equation. In particular, we incorporate an elastic scattering rate which is responsible for a finite resistivity at T = 0 and which is also always present in the experimental data (note, e.g., that in Fig. 1 of ref. ³, the reported resistivities are the difference with respect to their value extrapolated to T = 0).

Regarding the parameters of the fluctuations, these were extracted from RXS experiments on a NdBa₂Cu₃O_7−y sample, consistently leading to a deviation from linearity below T_FL ≈ 100 K in agreement with the resistivity data. Here, we consider the case of Nd-La_2−xSr_xCuO₄, where resistivity under strong magnetic fields is linear down to T ≈ 5 K. Unfortunately, although RXS experiments recently confirmed also for these cuprates the presence of CDFs with broad momentum distribution³³, detailed data are not available to extract their parameters. This is why we assume here that the parameters fitted from RXS data in NdBa₂Cu₃O_7−y are still reasonable estimates for Nd-La_2−xSr_xCuO₄ and we therefore use similar values: m = 10 meV, $\bar{\nu }=1.3$ eV (r.l.u.)⁻², $\bar{{{\Omega }}}=30$ meV. These values correspond to a rather short coherence length of a few lattice spacings, ${\xi }^{-1}=\sqrt{m/\bar{\nu }}\approx 0.1$ r.l.u.). We reiterate here that such a short coherence length of the CDFs is a crucial feature to obtain a nearly isotropic scattering over the Fermi surface, so that all quasiparticles are nearly equally scattered and their FL properties are uniformly spoiled. As far as the dissipation parameter is concerned, on the basis of the assumption c) given above, we adopt here a phenomenological form for the damping parameter

$$\gamma (p,T)={\left[A/{{{{{{\mathrm{log}}}}}}}\,\left(1+{T}_{0}/{{{\Theta }}}_{T}\right)+B| p-{p}_{{{{{{{{\rm{c}}}}}}}}}| \right]}^{-1},$$

(2)

where ${{{\Theta }}}_{T}=\min \ (T,\overline{T})$, and $\overline{T}$ sets the temperature scale above which the temperature dependence of γ saturates. Equation (2), with the parameters A, B, and T₀ adjusted to fit resistivity and specific heat data (see below), corresponds to the idea of a damping which increases by decreasing the temperature and is maximal at some doping p_c. The scale $\overline{T}$ is not constrained when fitting the low-temperature specific heat data, and we can only say that $\overline{T} {\,} > {\,}10$ K. Eq. (2) implies a dissipative QCP, with a diverging γ at T = 0 and p = p_c. This translates into the idea that the strange-metal behavior may eventually extend down to T = 0: as schematized in Fig. 1(c), an increasingly larger γ extends the linear resistivity to lower and lower temperatures. By consistently fitting the resistivity and specific heat data at various dopings (see below) we determine the parameters T₀ = 50 K, p_c = 0.235, A = 0.056, B = 0.87 for Nd-La_2−xSr_xCuO₄, and T₀ = 37 K, p_c = 0.232, A = 0.117, B = 2.84 for Eu-La_2−xSr_xCuO₄. We find that the linear resistivity extends down to a few Kelvins for the Nd-La_2−xSr_xCuO₄ sample at x = 0.24 (solid black circles and solid black curve in Fig. 2). The data taken in Eu-La_2−xSr_xCuO₄ with x = 0.24 (empty squares and dashed black curve in Fig. 2) seem instead to indicate that this sample is slightly away from the p ~ p_c condition and a deviation from linearity occurs at higher temperatures of a few tens of Kelvins. We point out that, strictly speaking, the so-called Planckian behavior^{28,34,35,36,37,38,39} is a precise way of achieving a linear dependence of the resistivity on the temperature, namely the scattering rate is proportional to the temperature with a prefactor of order one (in units where the Planck and Boltzmann constants are set equal to 1). In our theory, the scattering rate is proportional to the square of the coupling g between electron quasiparticles and fluctuations (see Eq. (5), in “Methods”), which is adjusted to fit the experimental resistivity curves, so our strange-metal behavior is not Planckian, in the sense that does not imply a universal relation between the scattering rate and the temperature. The very issue of the occurrence of a Planckian behavior in cuprates and other systems is controversial and debated^40,41.

Specific heat in cuprates

The phenomenological assumption of a large γ should be validated by investigating its effect on other observables. In particular, since we claim that the main physical effect of large damping is to shift the fluctuation spectral weight to lower energies, it is natural to expect a strong enhancement of the low-temperature specific heat. This is precisely what has been recently observed in other overdoped cuprates²⁶. Here we subtract from the observed specific heat the contribution of fermion quasiparticles. Despite the presence of a van Hove singularity, disorder, interplane coupling and electron–electron interactions smoothen this contribution. Thus fermion quasiparticles cannot account for the observed seemingly divergent specific heat.

We argue instead that an enhancement of the boson contribution to the specific heat occurs if γ obeys Eq. (2). The contribution of CDFs to the free energy density is ${f}_{{{{{{{{\rm{B}}}}}}}}}=\frac{T}{2N}{\sum }_{\ell }{\sum }_{{{{{{{{\bf{q}}}}}}}}}{{{{{{\mathrm{log}}}}}}}\,\left[{{{{{{{{\mathcal{D}}}}}}}}}^{-1}({{{{{{{\bf{q}}}}}}}},{{{\Omega }}}_{\ell })\right]$, where ${{{{{{{\mathcal{D}}}}}}}}$ is the Matsubara propagator obtained after analytical continuation of Eq. (1), Ω_ℓ = 2πℓT, with integer ℓ, and N is the number of unit cells. Hence, we obtain the contribution of damped CDFs to the internal energy density u_B and to the specific heat (details about the derivation are given in the “Methods” section)

$${C}_{V}^{{{{{{{{\rm{B}}}}}}}}}=\frac{\partial {u}_{{{{{{{{\rm{B}}}}}}}}}}{\partial T}=\frac{\partial }{\partial T}\left[\int\nolimits_{0}^{\infty }{{{{{{{\rm{d}}}}}}}}\omega \ \omega \ b(\omega )\ {\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )\right],$$

(3)

where ρ_B(ω) plays the role of an effective spectral density, whose full expression is given in the “Methods” section. The low-temperature asymptotic behavior of the specific heat is captured by the low-frequency asymptotic value

$${\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )\approx \frac{4\gamma }{\bar{\nu }}{{{{{{\mathrm{log}}}}}}}\,\left(1+\frac{\bar{\nu }}{4\pi \ m}\right).$$

Figure 3c shows that the enhancement of γ(T, p) leading to the observed linear-T behavior in the low-T resistivity, also induces a peak in the specific heat, due to the increase of low-energy boson degrees of freedom. Noticeably, the relative weight (height) of ${C}_{V}^{{{{{{{{\rm{B}}}}}}}}}$ at the various temperatures is well captured by our approach. In particular, this feature is mostly ruled by the Bose distribution function in Eq. (3) and depends only little on the specific expression of γ(T, p), provided enough spectral density is brought to frequencies ω ≲ T with increasing γ. We also notice that the logarithmic temperature dependence of γ mirrors in a nearly logarithmic behavior of C_V/T [see Fig. 3 (a, b)]. We point out that, within our phenomenological approach, it is difficult to estimate the real number of collective charge degrees of freedom contributing to the specific heat, and determine its numerical prefactor. For instance, assuming for the CDFs a correlation length ξ ≈ 1–2 wavelengths (of order 4–8 lattice units a), one could consider the CDF modes to live on the sites of a coarse-grained lattice. In this way, one could easily estimate that in two dimensions one CDF mode is present on a coarse-grained unit cell whose area may easily be 20–30 times the area of the original microscopic unit cell. This is why the CDF contribution to the specific heat might be rescaled by a seemingly large factor. We also emphasize the crucial difference between scenarios in which the increasing mass of the fermion quasiparticles⁴² (as a result e.g. of strong correlations and/or localization) leads to a diverging specific heat and our theory, where this is due to an increasing damping of the relevant collective modes. Within our approach, the fermion contribution to the specific heat is finite even when γ diverges at p = p_c.

Fig. 3: Specific heat.

Temperature dependence of the low-temperature specific heat per unit cell (u.c.) over temperature in Nd–La_2−xSr_xCuO₄ samples with doping p = 0.24 (black solid line and circles) and p = 0.22 (red solid line and diamonds) in linear (a) and semilogarithmic (b) [the theoretical curves have been rescaled by an overall factor 1/30, while keeping the relative weight at different doping and temperatures fixed - see the discussion about this prefactor after Eq. (3) in section “Specific heat in cuprates”]. c Doping dependence of the low-temperature C_V/T in Nd–La_2−xSr_xCuO₄ samples at different temperatures T = 0.5, 2.0, 10.0 K. Symbols represent the experimental data taken from ref. ²⁶, where the related error bars and the discussion of their origin can also be found, while the lines report our theoretical calculations.

Conclusion

The above analysis shows that two nontrivial features of the strange-metal behavior occurring near QCPs can be attributed to, and accounted for by, the damping parameter γ only. We still lack a microscopic scheme to determine the doping and temperature dependence of γ, and, within the scope of the present work, we rely on the phenomenological expression of Eq. (2). Therefore also the $T{{{{{{\mathrm{log}}}}}}}\,({T}_{0}/T)$ behavior of the specific heat at p_c is only phenomenologically captured by our theory. Nevertheless, we point out that our approach outlines a general paradigmatic change, shifting the relevance from the divergence of the correlation length ξ to the increase (possibly divergence) of dissipation. This is what renders our scheme different from the proposal of a local QCP put forward long ago in ref. ²². In this latter case the critical behavior of the imaginary part (i.e., damping) of the self-energy of the critical fluctuations, is sublinear iγ₀ω^1−α, which somehow rephrases our condition of an increasing damping at low energy scales by taking ${{{{{{{\rm{i}}}}}}}}{({\gamma }_{0}/\omega )}^{\alpha }\omega$ (i.e., γ ~ γ₀/ω^α), because of a diverging ξ. From our Eq. (2) one can see that the assumption that at p = p_c the scaling index in T for γ is zero, i.e., logarithmically divergent, suggests that α → 0 and the challenge is to obtain this result without ξ → ∞.

After momentum integration, a similar frequency dependence characterizes the singular dynamical interaction between quasiparticles mediated by the critical collective boson, in ref. ⁴³, where a complete analysis of the complementary problem of the competition between pairing and non-FL metal at a QCP is reported.

Of course, other, even more mundane, mechanisms might boost the increase of γ. In cuprates, for instance, p_c occurs at or very near a van Hove singularity, which enhances the density of states of fermions, thereby increasing the Landau damping γ of the fluctuations. Also the proximity to charge ordering might induce the reconstruction of the Fermi surface⁴⁴, thereby triggering an enhanced damping of the CDFs. In any case, while all these mechanisms are worth being explored to shape a microscopic theory of our scenario, it is clear that our phenomenological approach shifts the focus from diverging spacial correlations (and vanishing mass of the fluctuations) to a diverging damping of short-ranged fluctuations, thereby setting a new stage for the violation of the FL behavior.

Methods

The Boltzmann equation

The results for the in-plane resistivity presented in the paper are obtained within a Boltzmann equation approach, following the derivation of ref. ⁴⁵. We obtain

$$\frac{1}{\rho }=\frac{{e}^{2}}{{\pi }^{3}\hslash }\frac{2\pi }{d}\int \,{{{{{{{\rm{d}}}}}}}}\phi \ \frac{{k}_{{{{{{{{\rm{F}}}}}}}}}(\phi ){v}_{{{{{{{{\rm{F}}}}}}}}}(\phi ){\cos }^{2}(\phi -\eta )}{{{\Gamma }}(\phi )\cos (\eta )}\ ,$$

(4)

where k_F(ϕ), v_F(ϕ), and Γ(ϕ) denote the angular dependence of the Fermi momentum, Fermi velocity, and scattering rate along the Fermi surface and

$$\eta =\,{{\mbox{atan}}}\,\left(\frac{1}{{k}_{{{{{{{{\rm{F}}}}}}}}}}\frac{\partial {k}_{{{{{{{{\rm{F}}}}}}}}}}{\partial \phi }\right)\ .$$

The scattering rate Γ(ϕ) ≡ Γ₀ + Γ_Σ(ϕ) includes an elastic scattering rate Γ₀, and the scattering rate due to CDFs, ${{{\Gamma }}}_{{{\Sigma }}}(\phi )\equiv -{{{{{{{\rm{Im}}}}}}}}\ {{\Sigma }}({k}_{{{{{{{{\rm{F}}}}}}}}}(\phi ),\omega =0)$, where Σ(k, ω) is the electron self-energy [see ref. ²⁷ and its Supplementary Information].

The electron dispersion ε_k includes nearest-, next-nearest- and next-next-nearest-neighbor hopping terms generic for cuprates⁴⁶. The c-axis lattice constant for Nd-LSCO is taken as d ≈ 11 Å.

Calculation of the electron scattering rate

To obtain the electron scattering rate needed to calculate the electric transport, we carried out a perturbative calculation of the self-energy corrections of the fermion quasiparticles using the Feynman diagram of Fig. 4, where the solid line represents a bare quasiparticle, and the wavy line represents a CDF collective excitation.

Fig. 4: Electron self-energy.

Feynman diagram of the electron self-energy at the lowest perturbative order. The solid lines represent the electron propagator, while the wavy line represents the charge density fluctuation (CDF) propagator, Eq. (1).

The analytic expression for the (retarded) imaginary part is²⁷

$${{\mbox{Im}}}\;{{\Sigma }}({{{{{{{\bf{k}}}}}}}},\omega )= \, -{g}^{2}\int \frac{{{{{{{{\rm{{d}}}}}}}^{2}{{{{{{{\bf{q}}}}}}}}}}}{{(2\pi )}^{2}}\\ \, \times \frac{(\omega -{\varepsilon }_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{q}}}}}}}}})[b({\varepsilon }_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{q}}}}}}}}})+f({\varepsilon }_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{q}}}}}}}}}-\omega )]}{{[{\omega }_{0}+\bar{\nu }{\eta }_{{{{{{{{\bf{q}}}}}}}}}-{(\omega -{\varepsilon }_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{q}}}}}}}}})}^{2}/\overline{{{\Omega }}}]}^{2}+{(\omega -{\varepsilon }_{{{{{{{{\bf{k}}}}}}}}-{{{{{{{\bf{q}}}}}}}}})}^{2}},$$

(5)

where $b(z)={[{{{{{{{{\rm{e}}}}}}}}}^{z/{k}_{{{{{{{{\rm{B}}}}}}}}}T}-1]}^{-1}$ is the Bose function, $f(z)={[{{{{{{{{\rm{e}}}}}}}}}^{z/{k}_{{{{{{{{\rm{B}}}}}}}}}T}+1]}^{-1}$ is the Fermi function, g is the coupling between electrons and CDFs and ${\eta }_{q}=4-2\cos ({q}_{x}-{Q}_{x}^{c})-2\cos ({q}_{y}-{Q}_{y}^{c})$ contains the information about the CDF vector q_c. The parameter $\bar{\nu }$ should be scaled by 1/(2π)² ($\bar{\nu }\to \bar{\nu }/(4{\pi }^{2})$) if the momenta are given in r.l.u. as it is customary, e.g., in RXS experiments (see also below in the calculation of the specific heat). For the evaluation of ${{{\Gamma }}}_{{{\Sigma }}}\equiv {{{{{{{\rm{Im}}}}}}}}\ {{\Sigma }}({k}_{{{{{{{{\rm{F}}}}}}}}},0)$ we sum over all 4 equivalent wavevectors (±q_c, 0) and (0, ±q_c), with q_c ≈ 0.3 r.l.u.

Calculation of the specific heat

To define the specific heat contribution from a collective mode with finite lifetime we start from the free energy of a free boson in terms of its inverse propagator ${{{{{{{{\mathcal{D}}}}}}}}}^{-1}$ and we determine the effect of γ, by calculating the excess free energy

$$\delta {{{{{{{\mathcal{F}}}}}}}}=\frac{1}{2\beta }\mathop{\sum}\limits_{n,{{{{{{{\bf{q}}}}}}}}}\left[{{{{{{\mathrm{log}}}}}}}\,\left(\frac{{\omega }_{n}^{2}}{\overline{{{\Omega }}}}+\gamma | {\omega }_{n}| +{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)-{{{{{{\mathrm{log}}}}}}}\,\left(\frac{{\omega }_{n}^{2}}{\overline{{{\Omega }}}}+{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)\right].$$

Here, the second term represents the free energy of undamped “phonons” with dispersion ${\left(\overline{{{\Omega }}}{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)}^{1/2}$, which is subtracted to eliminate the most divergent term in the Matsubara frequency sum. The corresponding excess of internal energy is given by $\delta {{{{{{{\mathcal{U}}}}}}}}=\frac{\partial }{\partial \beta }(\beta \ \delta {{{{{{{\mathcal{F}}}}}}}}),$ (with $\beta =\frac{1}{{k}_{{{{{{{{\rm{B}}}}}}}}}T}$) finding

$$\delta {{{{{{{\mathcal{U}}}}}}}}={k}_{{{{{{{{\rm{B}}}}}}}}}T\mathop{\sum}\limits_{n,{{{{{{{\bf{q}}}}}}}}}\left[\frac{{\omega }_{{{{{{{{\bf{q}}}}}}}}}+\frac{1}{2}\gamma | {\omega }_{n}| }{\frac{{\omega }_{n}^{2}}{\overline{{{\Omega }}}}+\gamma | {\omega }_{n}| +{\omega }_{{{{{{{{\bf{q}}}}}}}}}}-\frac{{\omega }_{{{{{{{{\bf{q}}}}}}}}}}{\frac{{\omega }_{n}^{2}}{\overline{{{\Omega }}}}+{\omega }_{{{{{{{{\bf{q}}}}}}}}}}\right].$$

(6)

This expression allows us to define the internal energy of the damped CDFs as

$${{{{{{{\mathcal{U}}}}}}}}={k}_{{{{{{{{\rm{B}}}}}}}}}T\mathop{\sum}\limits_{n}\mathop{\sum}\limits_{{{{{{{{\bf{q}}}}}}}}}\frac{{\omega }_{{{{{{{{\bf{q}}}}}}}}}+\frac{1}{2}\gamma | {\omega }_{n}| }{\frac{{\omega }_{n}^{2}}{\overline{{{\Omega }}}}+\gamma | {\omega }_{n}| +{\omega }_{{{{{{{{\bf{q}}}}}}}}}}.$$

The Matsubara sum of the term with $\frac{1}{2}\gamma | {\omega }_{n}|$ in the numerator is formally divergent and therefore a convergency factor should be included as it is customary in diagrams with closed loops. By introducing the spectral representation of the boson propagator, and carrying out the Matsubara sum, the thermal part of the internal energy is obtained as

$${{{{{{{\mathcal{U}}}}}}}}=\mathop{\sum}\limits_{{{{{{{{\bf{q}}}}}}}}}\frac{1}{\pi }\int\nolimits_{0}^{\infty }{{{{{{{\rm{d}}}}}}}}\omega \ \frac{\gamma \omega \left(\frac{{\omega }^{2}}{\overline{{{\Omega }}}}+{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)}{{\left(\frac{{\omega }^{2}}{\overline{{{\Omega }}}}-{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)}^{2}+{\gamma }^{2}{\omega }^{2}}\ b(\omega ).$$

The specific heat is obtained by differentiating the internal energy with respect to T and dividing by the size of the system (e.g., the number N of unit cells), yielding

$${C}_{V}^{{{{{{{{\rm{B}}}}}}}}}=\frac{\partial }{\partial T}\int\nolimits_{0}^{\infty }{{{{{{{\rm{d}}}}}}}}\omega \ {\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )\ \omega \ b(\omega ),$$

(7)

where an effective density of states

$${\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )=\frac{1}{N}\mathop{\sum}\limits_{{{{{{{{\bf{q}}}}}}}}}\ \frac{1}{\pi }\frac{\gamma \left(\frac{{\omega }^{2}}{\overline{{{\Omega }}}}+{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)}{{\left(\frac{{\omega }^{2}}{\overline{{{\Omega }}}}-{\omega }_{{{{{{{{\bf{q}}}}}}}}}\right)}^{2}+{\gamma }^{2}{\omega }^{2}}$$

has been defined.

We consider a three-dimensional unit cell, but we assume that the dispersion in $\overrightarrow{q}$-space is only on the x, y plane. Introducing a density of states for the variable $\bar{\nu }| \overrightarrow{q}-{\overrightarrow{q}}_{{{{{{{{\rm{c}}}}}}}}}{| }^{2}$,

$$g(\varepsilon )=\frac{1}{N}\mathop{\sum}\limits_{{{{{{{{\bf{q}}}}}}}}}\ \delta (\bar{\nu }| \overrightarrow{q}-{\overrightarrow{q}}_{{{{{{{{\rm{c}}}}}}}}}{| }^{2}-\varepsilon )\approx \frac{1}{\pi \bar{\nu }}\theta ({{\Lambda }}-\varepsilon ),$$

where, in order to find an analytical expression, we approximate the quarter of the Brillouin zone with a circle centered at each of the four equivalent ${\overrightarrow{q}}_{{{{{{{{\rm{c}}}}}}}}}$, with radius $\bar{q}$, and ${{\Lambda }}\approx \bar{\nu }{\bar{q}}^{2}$. We then obtain the analytical expression of the effective spectral density of the CDF

$${\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )= \frac{\gamma }{2{\pi }^{2}\bar{\nu }}{{{{{{\mathrm{log}}}}}}}\,\frac{{\left(m\,+\,{{\Lambda }}\,-\,\frac{{\omega }^{2}}{\overline{{{\Omega }}}}\right)}^{2}+{\gamma }^{2}{\omega }^{2}}{{\left(m\,-\,\frac{{\omega }^{2}}{\overline{{{\Omega }}}}\right)}^{2}+{\gamma }^{2}{\omega }^{2}}\\ +\frac{2\omega }{{\pi }^{2}\bar{\nu }\ \overline{{{\Omega }}}}\left[\arctan \left(\frac{m+{{\Lambda }}}{\gamma \omega }-\frac{\omega }{\gamma \overline{{{\Omega }}}}\right)-\arctan \left(\frac{m}{\gamma \omega }-\frac{\omega }{\gamma \overline{{{\Omega }}}}\right)\right].$$

(8)

Since we are considering the limit of low temperatures it is reasonable to assume both $\omega \ \ll \ \sqrt{\overline{{{\Omega }}}(m+{{\Lambda }})}$ and γω ≪ m + Λ. In this regime, we can approximate ρ_B(ω) as ${\rho }_{{{{{{{{\rm{B}}}}}}}}}(\omega )\ \approx \ \frac{\gamma }{{\pi }^{2}\bar{\nu }}{{{{{{\mathrm{log}}}}}}}\,\left(1+\frac{{{\Lambda }}}{m}\right).$ If one uses r.l.u., then the replacement $\bar{\nu }\to \bar{\nu }/(4{\pi }^{2})$ must be performed, and one finds the expression for the low-frequency asymptotic behavior of ρ_B(ω) given in the main text.

The approximation becomes more and more accurate at lower and lower temperature. From this equation it is evident that ρ_B(ω) is a linear function of γ, and so is the specific heat. Since ρ_B(ω) is a constant function of ω in the regime of our interest, we get the explicit expression

$${C}_{V}^{{{{{{{{\rm{B}}}}}}}}}\approx \frac{\gamma }{{\pi }^{2}\bar{\nu }}{{{{{{\mathrm{log}}}}}}}\,\left(1+\frac{{{\Lambda }}}{m}\right)\frac{\partial }{\partial T}\left({k}_{{{{{{{{\rm{B}}}}}}}}}^{2}{T}^{2}\int\nolimits_{0}^{\infty }\frac{x}{{{{{{{{\rm{{e}}}}}}}^{x}-\; 1}}}{{{{{{{\rm{dx}}}}}}}}\right).$$

Our final expression for the ratio ${C}_{V}^{{{{{{{{\rm{B}}}}}}}}}/T$ is then

$$\frac{{C}_{V}^{{{{{{{{\rm{B}}}}}}}}}}{T}\ \ \approx \ \ {k}_{{{{{{{{\rm{B}}}}}}}}}^{2}\frac{\gamma }{3\bar{\nu }}{{{{{{\mathrm{log}}}}}}}\,\left(1+\frac{\pi \bar{\nu }}{m}\right).$$

Again, if one uses r.l.u., the substitution $\bar{\nu }\to \bar{\nu }/(4{\pi }^{2})$ must be performed.