Introduction

The dissipation of heat in nanoscale electronic devices has become a critical issue owing to their large interface density preventing heat conduction: e.g., SiO2 layer/Si for Si-based large scale integrated circuit (Fig. 1a). The interfaces complicate the comprehension of heat conduction in nanoscale world. Therefore, over the last few decades, academic research on nanoscale phonon transport in nanostructured materials with interfaces1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 has been intensively conducted to elucidate its mechanism and manage heat conduction16,17,18,19,20 in various scientific fields, such as thermoelectrics5,12,21,22, phonon engineering2,6,11, etc.

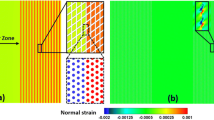
Fig. 1: Schematics of thermal transport physics through the interface.
figure 1

a Schematic of heat dissipation issue in large scale integrated circuit. b Phonon transport at the interface between materials A and B. c Small and d Large overlappings of vibron-phonon density-of-states (DOS) between amorphous and epitaxial crystals related to the large and small interface thermal resistance per unit area (ITR), respectively.

Full size image

In the nanoscale phonon transport, phonon transmission/scattering at the interface is one of the most profound topics to understand. Considerable effort has been made to understand the interface thermal resistance per unit area (ITR), such as the diffuse mismatch model, the molecular dynamics with specific interface models, and so on23,24,25,26. For example, calculations revealed that the ITR is decreased by a certain amount of compositional inhomogeneity near the interface24,26. In contrast, other calculations explained that the atomic-order segregation and inhomogeneity increase ITR23,25. Although the ITR at the specific interface can be calculated, it is hard to discuss the effect of certain interface structure parameters, such as inhomogeneity and strain, on the ITR in general. Then, it is actually difficult to predict the ITR in the realistic interface system with more complex structure, which comes from the discrepancy between the realistic interface and the ideal or simplified specific interface for calculation. From this background, we considered that it is demanded to reveal the universal physics of phonon transport across the interface by performing the research in the interface system without such discrepancy, namely realistic interface without complex structure. This universal physics leads to the establishment of a rough but versatile prediction method of ITR from the information of interface structure. The complex interface is usually composed of dissimilar materials (A and B) with different phonon properties; at the interface composed of quite different crystals, a “complex” interface layer possibly with large lattice strain, compositional inhomogeneity, and defects is formed (Fig. 1b). As the realistic interface system without complex structure to reveal phonon transport physics with versatility and universality, we propose an interface between amorphous material A/crystal material B, where lattice mismatch strain and associated defects are supposedly almost negligible. Assuming that a “complex” interface layer is not formed by the contact of amorphous A and crystal B, the phonon transport can be simply understood by basing on transition in quantum physics between the states of materials A and B with versatility and universality. This is similar to the electron transport case. Therein, when considering transition between the states of materials A and B, the interface layer for electrons is simply treated as the defect states, strain effect, and potential barrier.

Recently, deep understanding of phonon transport across amorphous/crystal interface is required because amorphous layers ubiquitously exist in nanoscale semiconductor crystal devices, which prevent heat dissipation resulting in negative influence on the electronic device characteristics. In amorphous materials, the vibron (extended phonon) works as a heat carrier. The vibron is classified into propagon, diffuson, and locon, each of which has different frequency ranges27,28. Their wave numbers are no longer good quantum numbers unlike the phonons in crystal. The vibron density-of-states (DOS) of amorphous material is smaller and flatter than phonon DOS of crystal composed of the same elements. Additionally, there is also mysterious problem about nanoscale phonon transport across the amorphous/crystal interface; the ITR at the amorphous/crystal interface is calculated to be small29,30,31 against the qualitative expectation of large ITR from small overlapping between small and flat vibron DOS in amorphous layer and phonon DOS with distinct peaks in epitaxial layer (Fig. 1c)32.

Here, we form amorphous-(a-) GeS/epitaxial-(e-) PbTe superlattice (SL) using hot wall epitaxy33 and experimentally extract ITR at the a-GeS/e-PbTe interface by measuring the temperature (T) dependence of thermal conductivity (κ) in a-GeS/e-PbTe SL. This ITR at the amorphous/epitaxial layer interface is extremely small (~0.8 ± 4.0 × 10−9 m2KW−1) compared with that at the epitaxial/epitaxial layer interface (e-PbS/e-GeTe) (~1.5 ± 0.6 × 10−8 m2KW−1). Furthermore, from ab initio lattice dynamics calculation and the above-mentioned experimental results, it is found that high phonon transmission through this interface can be predicted from large vibron-phonon DOS overlapping (Fig. 1d) and phonon group velocity (vg) similarity between propagon in amorphous layers and the “conventional” phonon in crystals. This demonstrates that controlling phonon (or vibron) DOS and vg similarity can be a comprehensive guideline to manage the heat conduction in nanoscale system with high-density interfaces.

Results and discussion

Formation of amorphous/epitaxial SLs

We formed two types of samples: e-PbS/e-GeTe SLs and a-GeS/e-PbTe SLs on BaF2(111) substrates, which are suitable stages to obtain higher ITR signal-to-noise ratio. By alternately depositing PbS and GeTe at 300 °C, e-PbS/e-GeTe SLs were successfully formed. Some of the e-PbS/e-GeTe SLs were annealed, resulting in the change from e-PbS/e-GeTe SLs to a-GeS/e-PbTe SLs through the atomic exchange of S and Te33 (See Supplementary Note 1). This structural change was observed using X-ray diffraction (See Supplementary Note 2). The total film thicknesses (d) were independently confirmed using scanning electron microscopy and a stylus profilometer (summarized with other structure information in Supplementary Note 2). Figure 2a shows a low-magnification cross-sectional bright-field transmission electron microscope (TEM) image of the annealed SL sample with a period thickness, L of ~100 nm. Figure 2b is a high-magnification scanning TEM (STEM) image, indicating the formation of a stacked structure with the layer thickness ratio of black and white regions to 1:1. To confirm the crystal structures of both layers, selective area electron diffraction (SAED) patterns of the black and white regions in Fig. 2b were observed, as shown in Fig. 2f and g, respectively. The SAED pattern of black region (Fig. 2f) corresponds to the theoretical pattern of single-crystalline PbTe with the epitaxial relationship of (111)PbTe//(111)BaF2. On the other hand, the SAED pattern of white region displayed amorphous pattern, as shown in Fig. 2g.

Fig. 2: Transmission electron microscopy results of a-GeS/e-PbTe superlattice.
figure 2

a Low-magnification cross-sectional bright-field transmission electron microscope (TEM) image of a-GeS/e-PbTe superlattice (SL). b High-magnification cross-sectional scanning TEM (STEM) image, c–e Energy dispersive X-ray spectroscopy (EDX) mapping images of c Pb, d Te, and e Ge in the same region of a-GeS/e-PbTe SL. f, g Selective area electron diffraction (SAED) patterns of f black and g white regions in a-GeS/e-PbTe SL.

Full size image

The compositions of the SL were analyzed by performing energy dispersive X-ray spectroscopy (EDX) measurements in the STEM image area (Fig. 2b). As shown in the EDX images (Fig. 2c and d), we observed considerably higher Pb and Te intensities in the black region. In the white region, the Ge intensity was higher in Fig. 2e. From these EDX and SAED results, it was found that black regions were epitaxial PbTe crystals with the relationship of (111)PbTe//(111)BaF2, whereas the white regions were amorphous GeS. This revealed that the a-GeS/e-PbTe SL was successfully formed by this atomic exchange technique33 although in general, epitaxial growth on an amorphous layer is basically difficult.

Thermal transport in e-PbS/e-GeTe SLs and a-GeS/e-PbTe SLs

Using 2ω method34,35,36, we measured the κ values of both e-PbS/e-GeTe SLs and a-GeS/e-PbTe SLs in the T range of 50–300 K to understand the phonon transport (See Supplementary Note 4). The κ was measured in the modulation frequency range with sufficiently high κ sensitivity in 2ω method, where the κ sensitivity was calculated in advance (See Supplementary Note 3). Figure 3a summarizes the T dependences of κ in e-PbS/e-GeTe SLs. The e-PbS/e-GeTe with the L of 70 nm exhibited remarkably low κ of 0.58 Wm−1K−1 at 300 K, which was approximately five times lower than those of GeTe crystal (3.0 Wm−1K−137) and PbS bulk crystal (2.5 Wm−1K−138). In SLs, there are a lot of interfaces that can scatter phonons. Hence, this lower κ value is considered to originate from strong interface phonon scattering. The T-κ data strongly depends on L. With decreasing L in e-PbS/e-GeTe SLs, T-κ data shifts downward. For example, at 300 K, the κ value of 0.58 Wm−1K−1 decreases to 0.45 Wm−1K−1 when L decreases from 70 to 30 nm; namely, κ is reduced with increasing interface density (decreasing L). This indicates that interface phonon scattering has a large influence on phonon transport, which supports that interface phonon scattering is the origin of the remarkably low κ value (Fig. 3e); namely, this κ includes the ITR component related to the interface phonon scattering.

Fig. 3: Thermal transport properties of superlattices.
figure 3

Temperature (T) dependences of thermal conductivity (κ) values a in e-PbS/e-GeTe superlattices (SLs) with period thicknesses (Ls) of 30 and 70 nm and (b) in a-GeS/e-PbTe SLs with Ls of 30, 70 and 80 nm (50–300 K). The experimental data of a-GeS/e-PbTe SL with L of 70 nm are fitted with Eq. (2), as shown by the broken curve in b. c, d L dependences of thermal resistances per unit area of one period structure (TRP) at 300 K in c e-PbS/e-GeTe and d a-GeS/e-PbTe SLs, respectively. The dotted and broken lines are the fitted curves of the experimental data of e-PbS/e-GeTe and a-GeS/e-PbTe SLs using Eq. (1), respectively. e, f Schematics of phonon transmission through e e-PbS/e-GeTe and f a-GeS/e-PbTe interfaces. g T dependence of interface thermal resistance per unit area (ITR) at a-GeS/e-PbTe interfaces. The error bars in a–d, g correspond to the standard deviations in the repeated measurements.

Full size image

To extract the ITR at the e-PbS/e-GeTe interface, the thermal resistances per unit area of one period structure (TRP) of e-PbS/e-GeTe SLs at 300 K were plotted as a function of L (Fig. 3c). When the number of period structures, n is large (>10), the thermal resistance per unit area (TR) of SL edges (surface and interface with substrate) is negligible compared with the total TR of SL, Rtot (=d/κ) in thermal circuit model, based on the material system used in this study. Then, the TRP of SL can be described as;

$${\mathrm{TRP}} = \frac{{R_{{\mathrm{tot}}}}}{n} \approx \rho _{{\mathrm{period}}}L + 2R_{{\mathop{\rm{int}}} }$$
(1)

where ρperiod is the effective thermal resistivity of the unit period structure without ITR contribution and Rint is an ITR. The value of 1/ρperiod is the effective thermal conductivity without ITR (κno_ITR). It is reported that, when the layer thickness is too small, Rint and ρperiod increase with decreasing thickness39. However, our present case is not in this situation because the phenomenon often occurs when the film thickness is <~30 nm from the viewpoint of phonon mean free path40,41. As indicated by Eq. (1), Rtot/n is proportional to L. The experimental data were best-fitted with Eq. (1) when ρperiod and Rint were adjusted to be ~1.2 ± 0.2 mKW−1 (mKW−1 indicates meter-KW−1) and ~1.5 ± 0.6 × 10−8 m2KW−1, respectively, as indicated by the dotted line in Fig. 3c. The uncertainties of ρperiod and Rint come from standard deviation in this fitting. The ρperiod was in close agreement with those of chalcogenide SL42,43. Thus, the linearity of the experimental values of Rtot/n and plausible ρperiod value guarantee the simple analysis using Eq. (1). The large ITR value (Rint) is comparable to the one at the other crystal/crystal interfaces (~3.3 × 10−8 m2KW−1 for crystal (c)-diamond/c-Si and ~3.3 × 10−8 m2KW−1 for c-GaN/c-Si)44,45.

Next, we measured the κ values of a-GeS/e-PbTe SLs with Ls of 30, 70, and 80 nm as a function of T (Fig. 3b). These samples exhibited almost the same κ values of ~0.6 Wm−1K−1 at 300 K and showed an increasing κ tendency with increasing T due to the increase of specific heat. Note that the κ values of a-GeS/e-PbTe SLs showed almost no L dependence unlike those of e-PbS/e-GeTe SLs. This result implies that a-GeS itself has a considerably higher TR than ITR of a-GeS/e-PbTe, making it difficult to detect the ITR contribution between a-GeS and e-PbTe46,47. As is the case with the ITR analysis of e-PbS/e-GeTe SLs, in order to extract ITR, we estimated the TRP values of a-GeS/e-PbTe SLs at 300 K as a function of L, as shown in Fig. 3d. The TRP values were best-fitted with the Eq. (1) (decision coefficient value of 0.91) when ρperiod and Rint were adjusted to be ~1.7 ± 0.1 mKW−1 and ~0.8 ± 4.0 × 10−9 m2KW−1, respectively. The uncertainties of ρperiod and Rint come from standard deviation in this fitting. The ITR at the a-GeS/e-PbTe interface (~0.8 ± 4.0 × 10−9 m2KW−1) is substantially smaller than that at the e-PbS/e-GeTe interface (~1.5 × 10−8 m2KW−1). It is also found that this ITR at the a-GeS/e-PbTe interface belongs to a class of small value by comparing with those at various amorphous/crystal interfaces (~3.5 × 10−9 m2KW−1 for a-SiO2/c-Al, ~1.3 × 10−9 m2KW−1 for a-Ge/c-Si, ~2.0–3.0 × 10−9 m2KW−1 for a-SiO2/c-Si29,30,31, and ~1.2 × 10−8 m2KW−1 for a-HfO2/c-Si48) although these interface materials with higher coordination numbers have the large dissimilarities at the either side of the interface in terms of atomic masses, chemical bonding and number densities of atoms unlike Ge, Si or polymers with the lower coordination numbers (around four or less). The obtained ρperiod value (~1.7 mKW−1) is in between the thermal resistivities of GeS (~3.3 mKW−1) and PbTe (~0.6 mKW−1) (Supplementary Note 5), which indicates the high reliability of this ITR analysis. We experimentally succeeded in extracting the extremely small ITR of the amorphous/epitaxial interface (Fig. 3f) by using a-GeS/e-PbTe SL although detecting ITR is basically difficult.

It was also observed that the ITR at the a-GeS/e-PbTe interface increased due to the decrease of phonon number with decreasing T (Fig. 3g), which tendency is similar to what occurred to the ITR at the crystal/crystal interface49. Here, the experimental measurement of the T dependence of ITR at the a-GeS/e-PbTe interface, which is basically difficult to detect, were successful only by using the present SLs with multiple a-GeS/e-PbTe interfaces and by extracting the ITR from the L-dependent κ at various T values.

First of all, for simple understanding of T-dependent κ in these amorphous/epitaxial SLs, we analyzed the κ results by using the theoretical expression of lattice thermal conductivity (κlat) based on Debye-Callaway model. Here, it is assumed that acoustic phonons mainly contribute to κlat, as reported in other works5,50. For simplicity, the phonon transport of three modes (one longitudinal and two transverse modes) is treated using an average velocity, v. In the structure model of PbTe/thin GeS SL, where the GeS layer with the interfaces is assumed as the interface layer for phonon scattering in the SL, the κlat can be described as follows (See Supplementary Note 6);

$$\kappa _{{\mathrm{lat}}} \approx \frac{{3k_B}}{{2\pi ^2\nu }}\left( {\frac{{k_B}}{\hbar }} \right)^3\int_{0}^{\theta _D/T} {\tau _c\frac{{x^4e^x}}{{\left( {e^x - 1} \right)^2}}} dx$$
(2)

where θD is the Debye temperature, kB is the Boltzmann constant, ħ is the reduced Planck constant, τc is the combined relaxation time, x = ħ ω/kBT, and ω is the angular frequency of the phonon. θD can be written as ħ (6π2Nv3)1/3/kB, where N is the atom density. τc−1 can be written as τUmklapp−1 + τimpurity−1 + τbdy−1 through Matthissen’s rule51, where τUmklapp, τimpurity, and τbdy are the relaxation times of Umklapp scattering, impurity scattering, and phonon scattering by the interface layer, respectively. The relaxation rates of impurity scattering τimpurity−1 and of Umklapp scattering τUmklapp−1 are given by τimpurity−1 = Aω4 and τUmklapp−1 = (ħ γG2/Mv2θD)ω2Texp(−θD/(3T)), respectively5, where A is constant value, γG is the Grüneisen parameter, and M is the average mass of atoms. The relaxation time of phonon scattering by the interface layer is expressed based on the concept of SL nanowire model50 as follows;

$$\tau _{{\mathrm{bdy}}}^{-1} = v\left({\frac{{\frac{3}{4}t_{{\mathrm{int}}}}}{{1-t_{{\mathrm{int}}}}}l}\right)^{-1}$$
(3)

where l is the average segment length and tint is the transmittance of the interface layer. The transmittance is simply expressed as tint = 1/(1 + γω/ωD)50,52,53, where γ is a constant value and ωD is the Debye angular frequency. The thermal transport analysis in the a-GeS/e-PbTe SLs with an L of 70 nm was performed by fitting the experimental data with Eqs. (2) and (3), where the ωD, N, γG, and M values of PbTe were used. The fitted results were v = 1888 ± 37 ms−1, A = 8.3 ± 1.6 × 10−42 s3, l = 32 ± 0.4 nm, and γ = 133 ± 1.9. The obtained v and l were almost equal to the reported average velocity (1770 ms−1) and the thickness of the PbTe layer (35 nm), respectively, validating this simple fitting analysis. The A value (8.3 × 10−42 s3) related to impurity scattering probability was three orders of magnitude higher than that of high-purity single-crystalline bulk Si (1.8 × 10−45 s3)50, which is found to be a reliable value by considering a larger amount of impurities in the present a-GeS/e-PbTe SLs than that in the single-crystalline Si. While this simple analysis helps us to understand overall T-dependent κ in the a-GeS/e-PbTe SLs, it does not bring the physics of the experimentally-obtained small ITR at the a-GeS/e-PbTe interface because the a-GeS layer was included in the effective interface layer for phonon scattering in this Debye-Callaway model analysis in addition to the a-GeS/e-PbTe interface (See Supplementary Note 6). Therefore, it is required to base on a phonon transport model at the a-GeS/e-PbTe interface without “complex” interface layer in order to comprehend the extremely small ITR at the a-GeS/e-PbTe interface.

High phonon transmission through the amorphous/epitaxial interface

One of the interesting experimental results is the extremely small ITR at the amorphous/epitaxial interface, which is in contrast with the qualitative expectation of large ITR based on quantum physics: small overlapping of vibron-phonon DOS between amorphous and epitaxial layers (Fig. 1c)32. Here, we aim at understanding the physics of the small ITR. For quasi-ballistic phonon transmission through the interface, “the conservation of energy and momentum” is essential. We calculated the DOSs of vibron in a-GeS and of a “conventional phonon” in single-crystalline GeS (c-GeS) and PbTe (c-PbTe) by lattice dynamics calculation. As shown in Fig. 4a, the vibron DOS of a-GeS in the frequency region of >~4 THz became flatter than phonon DOS of c-GeS, whereas the vibron DOS amplitude of a-GeS in the lower-frequency region (<~2 THz) is almost the same as phonon DOS of c-GeS. This relatively large vibron DOS of a-GeS in the lower-frequency region greatly overlapped with DOS of “conventional” phonon in c-PbTe, as shown in the conceptual schematics in Fig. 1d. This large DOS overlapping implies small ITR as is the case with the interface between solid and self-assembled monolayer54. The similarity of DOS amplitude between a-GeS and c-GeS in the low-frequency region presumably comes from the characteristics of acoustic-like vibrons and acoustic phonons. If vibron in the overlapped low-frequency region of a-GeS is the one with a large vg amplitude, which is the main heat carrier, such as propagon, the ITR is expected to become smaller. Therefore, we calculated the vg in a-GeS. For vg calculation, we are able to calculate band dispersions even for amorphous model approximately because we used finite size of supercells (See Supplementary Note 7). In addition, for more intuitive understanding, vibrons were classified into propagon, diffuson, and locon by using vg values (See Supplementary Note 7), as shown in Fig. 4b, demonstrating that there are many propagons in the overlapped low-frequency region (<~1.5 THz). Another important parameter for quasi-ballistic phonon transmission is the momentum conservation. However, the wave number of vibron in amorphous material is no longer a good quantum number unlike the phonon in the crystal. Hence, instead of the wave number, we focused on the similarity of vectors vgs between incident and transmitted phonons (vectors vgs in a-GeS (vGeS) and in c-PbTe (vPbTe)) for a comprehensive understanding. To consider the similarity, the correlation coefficients (vGeS·vPbTe/(|vGeS||vPbTe|)) and the amplitude ratio (|vGeS|/|vPbTe|) of the two vectors are shown for all vg pairs in Fig. 4c and d, respectively (Supplementary Note 10 and 11). Therein, the color displays the amplitude product (|vGeS| |vPbTe|) of the two vgs. The value of the |vGeS| |vPbTe| as a function of vibron frequency is shown in Fig. 4e. The vg amplitude is also key factor because the phonon with large vg amplitude can contribute to heat conduction largely. As shown by Fig. 4c and d, the vibron-phonon pairs that simultaneously have large correlation coefficients (~1) and amplitude ratio of ~1 are observed in the overlapped lower-frequency region. Furthermore, these pairs have large velocities, as indicated by the red color in Fig. 4c–e. These results indicate that the propagons in a-GeS and acoustic phonons in c-PbTe with large vg amplitude in the lower-frequency region have large vibron-phonon DOS overlapping and high vg similarity simultaneously. Based on these facts, it is considered that acoustic-like propagons and acoustic phonons that have large contributions to heat conduction can interact with each other, resulting in vibron/phonon transmission through the present amorphous/crystal interface quasi-ballistically (i.e., small scattering angles and energy loss). This high phonon transmission at the interface can explain the small ITR. It should be noted that in the present case, phonon transport across the interfaces can be simply discussed based on energy and momentum conservation such as quantum physics in the electron case. Therefore, if we can appropriately control the vibron-phonon DOS overlapping and vg similarity in the amorphous/crystal system without complex interface layers, heat issue in devices with large ITR can also be overcome.

Fig. 4: Lattice dynamics calculation results.
figure 4

a Phonon (or vibron) density-of-states (DOS) of c-PbTe, c-GeS, and a-GeS obtained by lattice dynamics calculation. b Vibron frequency dependence of phonon group velocity (vg) in a-GeS, where the vibron is classified into propagon, diffuson, and locon. c, d Vibron frequency dependence of c correlation coefficient (va-GeS·vPbTe/(|va-GeS||vPbTe|)) and d amplitude ratio (|va-GeS|/|vPbTe|) between va-GeS and vPbTe. The colors in c and d display the amplitude product (|va-GeS| |vPbTe|) of the two vgs. e Value of the amplitude product (|va-GeS| |vPbTe|) as a function of vibron frequency. va-GeS and vPbTe are defined as the vg vectors in a-GeS and c-PbTe, respectively.

Full size image

Conclusion

We experimentally demonstrated that the ITR at the a-GeS/e-PbTe interface was extremely small (~0.8 ± 4.0 × 10−9 m2KW−1) in the a-GeS/e-PbTe SLs compared to that at the epitaxial/epitaxial layer interface (e-PbS/e-GeTe) (~1.5 ± 0.6 × 10−8 m2KW−1). These ITR values were extracted by phonon transport analysis of L-dependent κ at various T values. The phonon (or vibron) DOS and vg obtained by the lattice dynamics calculation revealed that the small ITR at the a-GeS/e-PbTe interface is brought by large vibron-phonon DOS overlapping and high vg similarity between propagons (in the amorphous layer) and phonons (in the crystal layer). This result suggests that an appropriate design of phonon (or vibron) DOS and vg similarity is a key for managing the heat originating from nanoscale devices, which can overcome the heat issue in large scale integrated circuit.

Methods

Sample preparation

There are some difficulties in measuring the ITR at the amorphous/crystal interface because the large TR of amorphous layers hides the ITR contribution in TR measurement in general. The measurement of the SL including multiple amorphous/single crystal interfaces is one of the approaches to acquire a larger ITR signal. In this study, we formed a-GeS/e-PbTe SLs using hot wall epitaxy in the following process.

BaF2(111) substrates with dimension of 10 × 10 × 0.5 mm were introduced into a vacuum chamber equipped with Knudsen cells for PbS, Ca, and GeTe. Clean BaF2(111) surfaces were obtained by degassing at 500 °C for 10 min. As the initial layers for the growth of high-quality films, ~1 nm of PbS and several monolayers of Ca were alternately deposited on BaF2(111), where total thicknesses were ~10 nm. Subsequently, PbS and GeTe were alternately deposited on the initial layers at 300 °C33. To measure the ITR from the thickness dependence of κ, the SLs with the Ls of ~30–80 nm were formed at the thickness ratio of PbS and GeTe to 1:1. The e-PbS/e-GeTe SLs were annealed at 350 °C for 10 min under vacuum atmosphere, which resulted in the conversion of e-PbS/e-GeTe SL with the L to a-GeS/e-PbTe SL with the same L through atomic exchange. The thickness ratio of the a-GeS and e-PbTe layers was tuned to 1:1 in all the SLs.

Structural characterization

TEM analysis was performed using a JEM-2100F electron microscope (JEOL, Japan) at an accelerating voltage of 200 kV. The elemental distribution was analyzed using EDX in STEM mode. X-ray diffraction observation was carried out with a Cu Kα line (wavelength: 0.15418 nm).

Thermal conductivity measurement

The out-of-plane κ of the SLs was measured by 2ω method using a home-made 2ω apparatus, which method is already validated (See Supplementary Note 8 and 9). In this 2ω method34,35,36, κ is measured using the frequency domain, unlike time domain thermoreflectance method. A laser with a wavelength of 532 nm was used owing to the five times larger thermoreflectance coefficient of the Au transducer film than that in a commercial apparatus (ADVANCE-RIKO Inc., TCN-2ω) equipped with a He-Ne laser (635 nm)55. Au transducer films with a thickness of ~200 nm and a size of 2 × 4 mm were deposited on the surfaces of the samples. The electrodes were attached to the edges of the Au films using Ag pastes to improve the electrical contact. The Au films were Joule-heated by applying a sinusoidal voltage with a frequency of 200–10000 Hz between both edges of the Au films.

Phonon density-of-states and phonon group velocity calculations

Our calculations for electronic ground states and structure optimizations, including a-GeS, were carried out using the VASP code56,57. Amorphous models for a-GeS have finite supercell sizes that are inevitable in atomistic models58,59,60. As a consequence, non-zero volume of first Brillouin zone can be defined even for the amorphous models although this is usually a shortcoming of atomistic models. This enables us to calculate vg vectors throughout the first Brillouin zone. Looking at phonon (or vibron) DOS (Fig. 4a), small DOS of imaginary modes persists even after full structure optimization due to strong anharmonic nature of vibrons. The details are described in Supplementary Note 10 and 11.