Spontaneous PT-symmetry breaking in lasing dynamics

Abstract

Parity-time (PT) symmetric lasers exploit the modulation of optical gain and loss and have led to important fundamental demonstrations in non-Hermitian physics. The current theoretical analysis of PT-symmetric laser physics is performed on the basis of the adiabatic elimination of the medium polarization. This approximation doesn’t hold true for a more general optical system with strong photon-particle interactions, where the Rabi oscillation of active particles plays a non-negligible role in the lasing action. Here, we propose a model that takes into account the internal dynamics of active particles and numerically investigate the PT symmetry of macroscopic- and microscopic-sized laser systems that operate in the strong-coupling regime. The distinct phase diagrams are drawn according to the features of intracavity photon numbers and emission spectra. Our work extends the PT-symmetric optics from the weak- to the strong-coupling limit, potentially paving the way towards nonclassical PT-symmetric light sources for integrated photonic networks and ultrasensitive sensors.

Introduction

In quantum mechanics, the reality of a physical observable and the unitary dynamics for a quantum system rely on the fundamental postulate of the Hermiticity of the associated operators. However, this postulate has been questioned by the recent discovery that a non-Hermitian Hamiltonian with PT symmetry may also possess a real energy spectrum¹. Due to their high degree of flexibility and controllability, gain–loss-balanced optical systems provide a versatile platform to exploit the fundamental nature of the non-Hermitian PT-symmetric quantum mechanics in experiment². Thus far, a number of PT-symmetry-related phenomena, including spontaneous PT-symmetry breaking³, unidirectional invisibility⁴, and nonreciprocity⁵, have been observed for the propagation of light waves in a pair of coupled optical devices, such as waveguides and microcavities. Besides, the PT-symmetric optical platforms can also be employed in single dielectric nanoparticle/molecule detection, where the micrometer-sized sensors operate around the so-called exceptional points (EPs), potentially enhancing the sensitivity^6,7,8. In all these studies, two coupled optical waves (modes) follow the Schrödinger-type equation⁹

$${\mathrm{i}}\frac{{d}}{{{d}t}}\left( {\begin{array}{*{20}{c}} {{\cal{A}}_1\left( t \right)} \\ {{\cal{A}}_2\left( t \right)} \end{array}} \right) = H\left( {\begin{array}{*{20}{c}} {{\cal{A}}_1\left( t \right)} \\ {{\cal{A}}_2\left( t \right)} \end{array}} \right),$$

(1)

with the amplitudes ${\cal{A}}_{k = 1,2}( t ) = \sqrt {n_k( t )} \exp [ {{\mathrm{i}}\theta _k( t )} ]$, intensities (intracavity photon numbers) n_k = 1,2(t) and phases θ_k = 1,2(t) of the light fields. The two-dimensional Hamiltonian is given by

$$H = \left( {\begin{array}{*{20}{c}} {\it{\upxi }} & {g_{\mathrm{C}}} \\ {g_{\mathrm{C}}} & {{\it{\upxi }}^ \ast } \end{array}} \right),$$

(2)

with the complex optical gain/loss parameter ξ and the real interwave/intermode coupling strength g_C > 0. Obviously, H is non-Hermitian, H ≠ H^†, and owns the PT symmetry, PTH = HPT with the parity operator P = σ_x and the time-reversal operator T = K. Here, σ_x is the x-component of Pauli matrices and K denotes the complex conjugate operator. Comparing |Im ξ| and g_C, the coupled optical system exhibits two distinct phases. In the unbroken phase with |Im ξ| > g_C, the energy-level spectrum of H is entirely real-valued and the powers of two optical waves/modes and their power sum present an oscillatory behavior. By contrast, the eigenvalues of H become a pair of complex conjugates in the broken phase with |Im ξ| > g_C, where the amplitude of one supermode grows exponentially in time while the other decays.

Generally, the PT-symmetric optical platforms are divided into two groups according to the manner of their operation. In the passive group, the optical waves in the coupled system come from the external light sources. The transmitted beams from the system are measured to analyze the energy-level spectrum of H, where the locations and linewidths of the transmission peaks in the frequency domain correspond to the real and imaginary parts of the eigenvalues of H, respectively. However, the extra probe-beam noise inevitably influences the spectral purity of the transmission response. Furthermore, the transmission spectra cannot unveil some intrinsic properties of the coupled optical system (e.g., quantum correlation and statistics of photon emission) that are determined by the physical realization itself. In the active group^{10,11,12,13,14}, the coherent light waves are generated through the lasing action of the modes of interest and the intermode coupling is superimposed on the laser dynamics. The emission spectra are utilized to map the properties of the coupled system. Since no external light fields are introduced, these active platforms may reveal the nature of the PT-symmetric optics, compared to the passive ones. Thus far, the PT-symmetry breaking concept has been applied to interpret most experimental observations of various active optical schemes. A direct proof showing that the coupled laser system owns the PT symmetry from the measurement of the output light fields is still demanded. We notice that the emission spectra from a pair of PT-symmetric optical resonators were studied in theory¹⁵. However, the relevant optical scheme operates below or at the lasing threshold, rather than the lasing regime.

In addition, the current PT-symmetric optics is usually performed on the basis of the adiabatic elimination of the medium polarization^{16,17,18,19,20}. This adiabatic approximation is valid when the relaxation constant of the medium polarization much exceeds the cavity loss rates (i.e., the good-cavity limit) and the Rabi frequency associated with the light–particle interaction (i.e., the weak-coupling limit). The resulting rate equations for the coupled-cavity fields can be mapped onto the Schrödinger Eq. (1) with the Hamiltonian (2). Indeed, the rate-equation model is commonly employed to study, for example, the semiconductor lasers^10,11 but fails in describing the laser systems that operate in the strong light–particle coupling limit, such as the atomic gas/beam lasers^{21,22,23,24,25}. Hence, a more general study is necessary. Moreover, thus far, research has been carried out mainly on the classical optical systems. Suppressing the system’s size, which is measured by the numbers of particles and light quanta (photons), highlights the quantum behavior of the light–particle interaction and a full quantum treatment is needed²⁶. However, rare studies have been focused on the PT-symmetric optics in this regime.

In this paper, we numerically investigate the PT symmetry of an open system composed of a macroscopic/microscopic laser interacting with an empty optical cavity. In the model, we take into account the strong light–particle interaction, which makes the adiabatic elimination of the medium polarization become invalid. Our goal is to identify the PT-symmetry breaking through the measurements of the intracavity photon numbers and the emission spectra of the cavity fields. The macroscopic-sized system presents two steady-state lasing phases, where one denotes the PT-symmetry broken phase, while the other is non-PT-symmetric. The system’s phase diagram has one unstable lasing regime, which corresponds to the PT-symmetry unbroken phase, and one non-lasing regime. By contrast, the microscopic-sized system exhibits the steady-state PT-symmetry broken and unbroken phases. The phase transition is controlled via adjusting the intercavity coupling strength. Especially, the intensity auto- and cross-correlation functions of two cavity fields display the nonclassical behaviors of the photon emission of individual optical cavities and photon-pair generation. This microscopic-sized PT-symmetric lasing scheme has, to the best of our knowledge, not been studied before and may potentially operate as a nonclassical PT-symmetric light source in an integrated optical circuit. Our study explores the fundamental properties of PT-symmetric optics in the lasing regime, and our predictions can be tested by current microcavity and nanophotonic technologies.

Results and discussion

Macroscopic laser oscillation

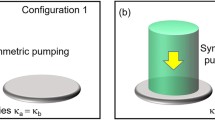
Figure 1a, b illustrate the macroscopic and microscopic optical systems, respectively, under study. We first consider the classical laser scheme shown in Fig. 1a. Two single-mode Fabry–Pérot cavities 1 and 2 are resonantly coupled by sharing one partial reflecting mirror, through which the photons inside one cavity enter into the other cavity at an effective rate $g_{\mathrm{C}}$. Two cavities have the same resonant frequency but their photon loss rates, denoted, respectively, by $\kappa _1$ and $\kappa _2$, may be different. An ensemble of active particles is located inside the active cavity 1, while the passive cavity 2 is empty. Each particle behaves independently of the others and is modeled by a two-state system that is composed of the upper $\left| e \rangle\right.$ and lower $\left| g \rangle\right.$ states. The lasing $\left| e \rangle\right. - \left| g \rangle\right.$ transition (frequency $\omega _0$) is resonantly coupled to the cavity 1 with a strength $g_{\mathrm{A}}$. The unavoidable dissipative processes (such as spontaneous emission) reduce the number of particles in $\left| e \rangle\right.$ and $| g \rangle$ at the rates $\gamma _e^{\prime}$ and $\gamma _g$, respectively. The decay rate of the particles from $\left| e \rangle\right.$ to $\left| g \rangle\right.$ is $\gamma _e$ (smaller than $\gamma _g$) and the particle polarization degrades at a rate $\gamma _{eg} = ( {\gamma _e^\prime + \gamma _g} )/2$. In what follows, we assume that the strong light–particle coupling regime with $4g_{\mathrm{A}}^2/\gamma _{eg}^2 \gg 1$ and $4g_{\mathrm{A}}^2/\kappa _1\gamma _{eg} \gg 1$ is accessed. The particles are pumped into $\left| e\rangle \right.$ at a rate $R$, producing the population inversion. The lasing action occurs once $R$ exceeds the total loss of the open system.

Fig. 1: Two coupled optical cavities in the lasing regime.

a Conventional laser system. Two Fabry–Pérot cavities 1 and 2 share the same mirror (purple disc), resulting in an intercavity coupling strength $g_{\mathrm{C}}$. The photon loss rates of two cavities are $\kappa _1$ and $\kappa _2$, respectively. The active particles are located inside cavity 1, which is coupled to the laser transition of the particles with a strength $g_{\mathrm{A}}$. The laser transition is formed by a pair of upper $\left| e \rangle\right.$ and lower $\left| g\rangle \right.$ levels of particle. The particles are pumped onto $\left| e\rangle \right.$ at a rate $R$. The $\left| e\rangle \right.$-populated particles decay at a rate $\gamma _e^\prime$, where the decay rate corresponding to the $\left| e \rangle\right. - \left| g \rangle\right.$ branch is $\gamma _e$. The decay rate of the $\left| g \rangle\right.$-populated particles is $\gamma _g$. The relaxation constant of the particle polarization is $\gamma _{eg} = ( {\gamma _e^\prime + \gamma _g} )/2$. In this study, we set $\kappa _2 = 2\kappa _1$, $\gamma _e = 10\kappa _1$, and $\gamma _e^\prime = \gamma _g = g_{\mathrm{A}} = 20\kappa _1$ and the strong-coupling regime with $g_{\mathrm{A}} > ( {\kappa _1,\gamma _{eg}})$ is accessed. b One-particle laser. An active particle is placed inside cavity 1. The particle is characterized by four states, where a pump light drives the $\left| 1\rangle \right. - \left| 4\rangle \right.$ transition with a strength ${\mathrm{{\Omega}}}$ and the coupling strength between the lasing $\left| 2\rangle \right. - \left| 3\rangle \right.$ transition and cavity 1 is $g_{\mathrm{A}}$. The population inversion is achieved via the spontaneous emission from $\left| 4\rangle \right.$ to $\left| 3\rangle \right.$. The decay rate of the particle from $\left| i \rangle\right.$ to $\left| j \rangle\right.$ with $i,j = 1,2,3,4$ and $i > j$ is defined as $\gamma _{ij}$. The cross-coincidence of the photon emissions from the two cavities is measured by two photodetectors (PDs) that are, respectively, placed in front of two output cavity mirrors. We set $\gamma _{41} = \gamma _{43} = \gamma _{31} = \gamma _{32} = 10\kappa _1$, $\gamma _{42} = \kappa _1$, $\gamma _{21} = 20\kappa _1$, $\kappa _2 = 2\kappa _1$, and ${\mathrm{{\Omega}}} = g_{\mathrm{A}} = 40\kappa _1$ and the strong-coupling limit, that is, $4g_{\mathrm{A}}^2/{\mathrm{{\Gamma}}}_{32}^2 \gg 1$ and $4g_{\mathrm{A}}^2/\kappa _1{\mathrm{{\Gamma}}}_{32} \gg 1$ with ${\mathrm{{\Gamma}}}_{32} = \left( {\gamma _{32} + \gamma _{31} + \gamma _{21}} \right)/2$, is reached.

We emphasize that the diagram shown in Fig. 1a just presents one feasible coupling scheme. There are also other ways to achieve the intercavity coupling, for example, the spatial/spectral overlap between two whispering gallery modes^5,27 (WGMs), the photonic crystal (PhC) microcavities in one slab with asymmetric optical gains¹², and the electric/magnetic coupling between superconducting circuits²⁸. The quality factor of a glass WGM microsphere²⁹ can reach as high as $8 \times 10^9$, corresponding a photon loss rate of a few $10^5$ s⁻¹ for a light wavelength of 800 nm. While the PhC microcavities³⁰ have the relatively low-quality factors (up to $10^7$), the intercavity coupling strength may greatly exceed the cavity loss rates, $g_{\mathrm{C}} \gg \kappa _{k = 1,2}$. By contrast, the superconducting cavities, operating at a frequency of a few GHz, have the advantages of flexibility, tunability, and scalability, but their quality factors are much lower (~10³). The optical gain materials inside cavity 1 can be four-level atomic gases^21,24, fluorescent dye molecules³¹, ion-doped crystals^32,33, two-level atomic beams^22,25, and superconducting qubits³⁴. Recent experiments^35,36,37 have manifested the strong (artificial) particle–cavity coupling.

The open system described above may be investigated by using the Heisenberg–Langevin approach³⁴ (Supplementary Note 1). The equations of motion of the modified cavity fields ${\mathcal{A}}_{k = 1,2}\left( t \right) = \sqrt {n_k\left( t \right)} {\mathrm{e}}^{{\mathrm{i}}\theta _k\left( t \right)}$ still take the form of Eq. (1) but with a different expression of the Hamiltonian

$$H = \left( {\begin{array}{*{20}{c}} {G\left( t \right)} & {g_{\mathrm{C}}} \\ {g_{\mathrm{C}}} & {L\left( t \right)} \end{array}} \right).$$

(3)

Here, $\theta _{k = 1,2}\left( t \right)$ denote the cavity-field phases relative to that of the macroscopic medium polarization. The diagonal elements $G\left( t \right)$ and $L\left( t \right)$ depend on the macroscopic variables (i.e., polarization and populations in two laser states) of the active particles and represent the net optical gain (in cavity 1) and loss (in cavity 2), respectively (see Supplementary Equations S8a and S8b). The non-diagonal elements account for the energy exchange between two cavity fields through the shared mirror. In general, $G\left( t \right)$ and $L\left( t \right)$ are complex and the common gain–loss balance $G\left( t \right) = L^ \ast \left( t \right)$ is not maintained at any time. One may rewrite Eq. (3) as

$${\mathrm{i}}\frac{{d}}{{{d}t}}\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_1\left( t \right)} \\ {{\mathcal{A}}_2\left( t \right)} \end{array}} \right) = {\mathcal{H}}\left( t \right)\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_1\left( t \right)} \\ {{\mathcal{A}}_2\left( t \right)} \end{array}} \right) - \lambda \left( t \right)\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_1\left( t \right)} \\ {{\mathcal{A}}_2\left( t \right)} \end{array}} \right)\\ \;{\mathrm{with}}\;{\mathcal{H}}\left( t \right) = \left( {\begin{array}{*{20}{c}} {\mu \left( t \right)} & {g_{\mathrm{C}}} \\ {g_{\mathrm{C}}} & { - \mu \left( t \right)} \end{array}} \right).$$

(4)

Here, we have defined the diagonal element $\mu \left( t \right) = \left( {G\left( t \right) - L\left( t \right)} \right)/2$ and the bias $\lambda \left( t \right) = - \left( {G\left( t \right) + L\left( t \right)} \right)/2$. The time-dependent ${\mathcal{H}}\left( t \right)$ can be interpreted as an energy-shifted Hamiltonian.

In the laser dynamics, the pump process continuously injects the energy into the open system, while the unavoidable decay sources, such as the spontaneous emission of the active particles and the photons escaping from the optical cavities, dissipate the system’s energy into the environment. The balance of these two processes brings the open system to a steady state (denoted by the subscript ss) when the time scale of interest is much longer than the lifetimes of particle states and intracavity photons. Consequently, Eq. (4) is reduced to a time-independent Schrödinger-like equation

$${\mathcal{H}}_{{\mathrm{ss}}}\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_{{\mathrm{ss}},1}} \\ {{\mathcal{A}}_{{\mathrm{ss}},2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\mu _{{\mathrm{ss}}}} & {g_C} \\ {g_{\mathrm{C}}} & { - \mu _{{\mathrm{ss}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_{{\mathrm{ss}},1}} \\ {{\mathcal{A}}_{{\mathrm{ss}},2}} \end{array}} \right) = \lambda _{{\mathrm{ss}}}\left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_{{\mathrm{ss}},1}} \\ {{\mathcal{A}}_{{\mathrm{ss}},2}} \end{array}} \right),$$

(5)

with $\mu _{{\mathrm{ss}}} = \left( {G_{{\mathrm{ss}}} - L_{{\mathrm{ss}}}} \right)/2$ and $\lambda _{{\mathrm{ss}}} = - \left( {G_{{\mathrm{ss}}} + L_{{\mathrm{ss}}}} \right)/2$ (see Supplementary Equations S12a and S12b). When $\mu _{{\mathrm{ss}}}$ is real, the shifted Hamiltonian ${\mathcal{H}}_{{\mathrm{ss}}}$ possesses the Hermiticity, ${\mathcal{H}}_{{\mathrm{ss}}}^\dagger = {\mathcal{H}}_{{\mathrm{ss}}}$. By contrast, ${\mathcal{H}}_{{\mathrm{ss}}}$ satisfies the PT symmetry, $PT{\mathcal{H}}_{{\mathrm{ss}}} = {\mathcal{H}}_{{\mathrm{ss}}}PT$, when $\mu _{{\mathrm{ss}}}$ is purely imaginary. For the PT-symmetric ${\mathcal{H}}_{{\mathrm{ss}}}$, the coupled system is in the unbroken (broken) phase when the eigenvalue $\lambda _{{\mathrm{ss}}}$ is real (complex). In addition, a steady-state solution of the open system may be not stable, that is, an arbitrary small perturbation can take the system away from the steady state. Thus, the linear analysis needs to be performed to examine the stability of a steady-state solution (Supplementary Note 1).

Figure 2a illustrates the stable steady-state solutions of the intracavity photon numbers $n_{{\mathrm{ss}},k = 1,2}$. Two distinct lasing phases are presented, corresponding to two sets of ${\mathcal{A}}_{{\mathrm{ss}},k = 1,2}$, respectively (see Supplementary Equations S9–S11). In phase 1, $n_{{\mathrm{ss}},1}$ is higher than $n_{{\mathrm{ss}},2}$ since the photons inside the cavity 2 are entirely from the cavity 1. Raising the pumping rate $R$ enhances both $n_{{\mathrm{ss}},k = 1,2}$. As $g_{\mathrm{C}}$ is increased, more photons inside cavity 1 can enter cavity 2 through the shared mirror before leaking out of cavity 1. Hence, $n_{{\mathrm{ss}},1}$ falls while $n_{{\mathrm{ss}},2}$ rises. Surprisingly, $n_{{\mathrm{ss}},2}$ slightly exceeds $n_{{\mathrm{ss}},1}$ when $g_{\mathrm{C}}$ approaches the phase boundary that is determined by the stability of the steady-state solutions. In addition, varying $g_{\mathrm{C}}$ does not change the cavity-field phase $\theta _{{\mathrm{ss}},1}$ and also two cavity fields maintain a constant phase difference $( {\theta _{{\mathrm{ss}},1} - \theta _{{\mathrm{ss}},2}})$ for an arbitrary $g_{\mathrm{C}}$ (Fig. 2b). This may be interpreted as follows: The intercavity coupling modulates the laser dynamics in cavity 1. For a weak $g_{\mathrm{C}}$, the relatively fast cavity losses $\kappa _{1,2}$ and medium-polarization relaxation $\gamma _{eg}$ erase the modulation effects on two cavity-field phases $\theta _{{\mathrm{ss}},k = 1,2}$ within a time scale much shorter than $g_{\mathrm{C}}^{ - 1}$. Thus, $\theta _{{\mathrm{ss}},k = 1,2}$ are completely determined by the light source, that is, the medium polarization, except the extra constant phase offsets. Actually, the fixed value of $\theta _{{\mathrm{ss}},1}$ maximizes the interaction of the active particles with cavity 1. Moreover, it is found that in the lasing phase 1 both $\mu _{{\mathrm{ss}}}$ and $\lambda _{{\mathrm{ss}}}$ are purely imaginary and one has ${\mathrm{Im}}\left( {\mu _{{\mathrm{ss}}}} \right) \,> \, 0$ and ${\mathrm{Im}}\left( {\lambda _{{\mathrm{ss}}}} \right) \,<\, 0$. Thus, the shifted Hamiltonian ${\mathcal{H}}_{{\mathrm{ss}}}$ has PT symmetry and the coupled system is in the broken phase. Figure 2c displays the dependence of the emission spectra $S_{k = 1,2}\left( \omega \right)$ of two cavity fields on $g_{\mathrm{C}}$ (see “Methods”). It is seen that only one spectral peak is presented for either cavity field. Interestingly, the spectral linewidth of cavity field 2 is always narrower than that of cavity field 1, despite the fact that cavity field 2 completely comes from cavity field 1. Increasing $g_{\mathrm{C}}$ broadens both spectra. In particular, the spectral peak of $S_1\left( \omega \right)$ presents a nearly flat top when the coupled system operates in the vicinity of the phase boundary, denoting the onset of the spectral splitting.

Fig. 2: Steady-state solutions of the conventional laser system.

a Dependence of the intracavity photon numbers $n_{{\mathrm{ss}},k = 1,2}$ on the pumping rate $R$ and the intercavity coupling strength $g_{\mathrm{C}}$. Here, the subscript ss represents the steady-state solutions and $k = 1,2$ denote the cavity 1 and 2, respectively. The photon loss rate $\kappa _1$ of the cavity 1 is chosen as the frequency unit in the plot. Four distinct regimes are presented. In the phase 1, $n_{{\mathrm{ss}},1}$ decreases, while $n_{{\mathrm{ss}},2}$ increases as $g_{\mathrm{C}}$ is enhanced. In the phase 2, $n_{{\mathrm{ss}},k = 1,2}$ are nearly equal and slowly degrade when $g_{\mathrm{C}}$ grows. In the unstable regime, both $n_{k = 1,2}$ vary periodically in time. In the rest regime, both $n_{{\mathrm{ss}},k = 1,2}$ stay at zero, that is, no lasing action occurs. b Steady-state cavity-field phases $\theta _{{\mathrm{ss}},1}$ and $( {\theta _{{\mathrm{ss}},1} - \theta _{{\mathrm{ss}},2}})$ as a function of $g_{\mathrm{C}}$. The pumping rate is fixed at $R/\kappa _1 = 300$. In the phase 1, both $\theta _{{\mathrm{ss}},1}$ and $( {\theta _{{\mathrm{ss}},1} - \theta _{{\mathrm{ss}},2}} )$ maintain constant. In the phase 2, the phases vary with $g_{\mathrm{C}}$. c Emission spectra of two cavity fields $S_1\left( \omega \right)$ (red) and $S_2\left( \omega \right)$ (blue) at several selected values of $g_{\mathrm{C}}$. Here, $\omega$ denotes the angular frequency in the frequency domain via the Fourier transform and $\omega _0$ corresponds to the central frequency of the laser transition. The pumping rate is set at $R/\kappa _1 = 300$. The symbols are obtained from the numerical simulation, while the solid and dashed curves correspond to the curve fitting. The full width at half-maximum of each spectral curve has been inserted.

In the lasing phase 2, both $n_{{\mathrm{ss}},k = 1,2}$ degrade slowly as $g_{\mathrm{C}}$ is increased. The analytical expressions of the steady-state solutions (see Supplementary Equations S9–S11) illustrate that for a large $g_{\mathrm{C}}$ the effect of the intercavity coupling on ${\mathcal{A}}_{{\mathrm{ss}},1}$ is so strong that $\theta _{{\mathrm{ss}},1}$ can no longer sustain the maximum light–particle interaction in cavity 1 but has to be shifted, thereby attenuating the lasing action. Also, $( {\theta _{{\mathrm{ss}},1} - \theta _{{\mathrm{ss}},2}})$ becomes $g_{\mathrm{C}}$-dependent (see Fig. 2b) and this weakens the intercavity coupling. The boundary between phases 1 and 2 depends solely upon $g_{\mathrm{C}}$ (see Fig. 2a) and the relevant phase transition is found to be of the second order. Within the regime of phase 2, the parameter $\mu _{{\mathrm{ss}}}$ in Eq. (5) is complex but not purely imaginary. One may interpret this as follows: The shifted $\theta _{{\mathrm{ss}},1}$ (compared to the value in the lasing phase 1) effectively introduces an extra frequency shift to cavity field 1 (see Supplementary Equations S12a and S12b), thereby lifting the degeneracy of two cavity modes and resulting in ${\Re} \left( {\mu _{{\mathrm{ss}}}} \right) \ne 0$. Thus, the Hamiltonian ${\mathcal{H}}_{\mathrm{ss}}$ does not possess the PT symmetry, $PT{\mathcal{H}}_{{\mathrm{ss}}} \ne {\mathcal{H}}_{{\mathrm{ss}}}PT$, in the lasing phase 2. Varying ${\mathrm{g}}_{\mathrm{C}}$ from phase 1 to phase 2 breaks the PT symmetry of ${\mathcal{H}}_{{\mathrm{ss}}}$. This is unlike the common PT-symmetry breaking, where the intercavity coupling affects the reality of the energy-level spectrum of a PT-symmetric Hamiltonian. By using Supplementary Equations S11d–S11e, the ratio of $n_{{\mathrm{ss}},1}$ to $n_{{\mathrm{ss}},2}$ is derived as $n_{{\mathrm{ss}},1}/n_{{\mathrm{ss}},2} = ( {2\gamma _{eg} - \kappa _2} )/( {2\gamma _{eg} + \kappa _1})$ in the lasing phase 2. The two cavities have different photon numbers, $n_{{\mathrm{ss}},1} < n_{{\mathrm{ss}},2}$, for a finite $\gamma _{eg}$. In the limit $\gamma _{eg} \gg \kappa _{1,2}$, where the approximation of adiabatically eliminating the medium polarization becomes valid, the relative difference $\frac{{| {n_{{\mathrm{ss}},1} - n_{{\mathrm{ss}},2}} |}}{{n_{{\mathrm{ss}},k = 1,2}}}$ is significantly suppressed and one approximately obtains $n_{{\mathrm{ss}},1} = n_{{\mathrm{ss}},2}$. This result corresponds to the unbroken phase of a conventional PT-symmetric coupled-cavity system. Thus, the conventional unbroken PT-symmetric phase is actually an idealization in the adiabatic limit. As depicted in Fig. 2c, two cavity fields have the similar spectral profiles, $S_1\left( \omega \right) \approx S_2\left( \omega \right)$. The strong intercavity coupling gives rise to a spectral splitting whose separation is determined by $2g_{\mathrm{C}}$.

When the intercavity coupling strength $g_{\mathrm{C}}$ is further enhanced, the coupled system is no longer allowed to stay in a steady state in a stable manner. This is because none of the steady-state $\theta _{{\mathrm{ss}},k = 1,2}$ enable the laser dynamics in the cavity 1 to follow the modulation of the intercavity coupling. As shown in Fig. 3a, both $n_{k = 1,2}\left( t \right)$ oscillate at a frequency about $g_{\mathrm{C}}$ and the two oscillations are nearly out of phase, indicating the two cavities exchange the energy periodically. The total photon number $\left( {n_1\left( t \right) + n_2\left( t \right)} \right)$ also shows an oscillatory behavior. To understand the mechanics behind this, we define

$$\left( {\begin{array}{*{20}{c}} {{\mathcal{B}}_1\left( t \right)} \\ {{\mathcal{B}}_2\left( t \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathcal{A}}_1\left( t \right)} \\ {{\mathcal{A}}_2\left( t \right)} \end{array}} \right){\mathrm{e}}^{ - {\mathrm{i}}\mathop {\smallint }\limits_{ - \infty }^t \lambda \left( {t^{\prime} } \right){\mathrm{d}}t^{\prime}},$$

(6)

and Eq. (4) is then re-expressed as a time-dependent Schrödinger-like equation

$${\mathrm{i}}\frac{{d}}{{{{d}}t}}\left( {\begin{array}{*{20}{c}} {{\mathcal{B}}_1\left( t \right)} \\ {{\mathcal{B}}_2\left( t \right)} \end{array}} \right) = {\mathcal{H}}\left( t \right)\left( {\begin{array}{*{20}{c}} {{\mathcal{B}}_1\left( t \right)} \\ {{\mathcal{B}}_2\left( t \right)} \end{array}} \right).$$

(7)

Fig. 3: Unstable lasing dynamics.

a Time-dependent intensities of two cavity fields $n_{k = 1,2}\left( t \right)$ with the intercavity coupling strength $g_{\mathrm{C}}/\kappa _1 = 99$. Here, $k = 1,2$ denote the cavities 1 and 2, respectively, and the photon loss rate $\kappa _1$ of cavity 1 is chosen as the frequency unit in the plot. Both $n_{k = 1,2}\left( t \right)$ vary periodically with a period of about $g_{\mathrm{C}}^{ - 1}$. b Time evolution of the diagonal element $\mu \left( t \right)$ of the Hamiltonian ${\mathcal{H}}\left( t \right)$ with $g_{\mathrm{C}}/\kappa _1 = 99$. The real part of $\mu \left( t \right)$ maintains at zero, while its imaginary part varies periodically and diverges within a short duration around $n_1\left( t \right)\sim 0$. c Numerical simulation of the emission spectrum $S_1\left( \omega \right)$ of cavity field 1 (red filled circles) with $g_{\mathrm{C}}/\kappa _1 = 99$. Here, $\omega$ denotes the angular frequency in the frequency domain and $\omega _0$ is the central frequency of the laser transition. Only the spectral section on the blue-detuned side is presented and its mirror image gives the spectral section on the red-detuned side. The solid line corresponds to the curve fitting. The spectrum $S_2\left( \omega \right)$ of cavity field 2 shows a nearly identical line shape. d Time-averaged intracavity intensities $\bar n_{k = 1,2} = \frac{1}{{{\mathrm{{\Delta}}}t}}\mathop {\smallint }\nolimits_{t_0}^{t_0 + {\mathrm{{\Delta}}}t} n_{k = 1,2}\left( t \right){\mathrm{d}}t$ with an arbitrary initial time $t_0$ and a time duration ${\mathrm{{\Delta}}}t\sim g_{\mathrm{C}}^{ - 1}$ vs. the intercavity coupling strength $g_{\mathrm{C}}$. In the stable steady-state (denoted by the subscript ss) regime, we have $\bar n_{k = 1,2}$ are equal to the steady-state values $n_{{\mathrm{ss}},k = 1,2}$ of two cavity fields. For all plots, the pumping rate $R$ is set at $R/\kappa _1 = 300$.

Figure 3b displays an example of the diagonal element $\mu \left( t \right)$ of ${\mathcal{H}}\left( t \right)$. It is seen that $\mu \left( t \right)$ is purely imaginary, meaning ${\mathcal{H}}\left( t \right)$ possesses the PT symmetry, $PT{\mathcal{H}}\left( t \right) = {\mathcal{H}}\left( t \right)PT$. In addition, although ${\mathrm{Im}}\left[ {\mu \left( t \right)} \right]$ exhibits a dispersion behavior around $n_1\left( t \right)\sim 0$, $\left| {\mu \left( t \right)} \right|$ is smaller than the off-diagonal elements $g_{\mathrm{C}}$ of ${\mathcal{H}}\left( t \right)$. Thus, the two eigenvalues of ${\mathcal{H}}\left( t \right)$ are both real at any time, that is, the coupled system is in the PT-symmetry unbroken phase. The transition from the lasing phase 2 to the unstable regime hardly affects the spectral profiles of two cavity fields (see Fig. 3c). Figure 3d illustrates the dependence of the time-averaged intensities $\bar n_{k = 1,2} = \frac{1}{{{\mathrm{{\Delta}}}t}}\mathop {\smallint }\nolimits_{t_0}^{t_0 + {\mathrm{{\Delta}}}t} n_k\left( t \right){\mathrm{d}}t$ with ${\mathrm{{\Delta}}}t\sim g_{\mathrm{C}}^{ - 1}$ on $g_{\mathrm{C}}$, where $\bar n_{k = 1,2}$ first go up and then fall to zero as $g_{\mathrm{C}}$ is increased. The boundary of the unstable regime on the high-$g_{\mathrm{C}}$ side is determined by the threshold of the steady-state laser solutions, beyond which the lasing action ceases because the strong mode splitting caused by the intercavity interaction pushes the modes out of the gain spectrum of the medium polarization.

The phase diagram of the macroscopic coupled system in the $R - g_{\mathrm{C}}$ plane is summarized in Fig. 4, where the phase boundaries are determined by the lasing thresholds (TH1 and TH2) and the linear stability analysis (ST1 and ST2) of the steady-state solutions ${\mathcal{A}}_{{\mathrm{ss}},k = 1,2}$. The lasing phase 1 is surrounded by a section of the TH1 line and the ST1 line. In this phase, $\theta _{{\mathrm{ss}},k = 1,2}$ are $g_{\mathrm{C}}$-independent and maximize both the light–particle interaction in cavity 1 and the intercavity coupling. The steady-state energy-shifted Hamiltonian ${\mathcal{H}}_{{\mathrm{ss}}}$ is PT symmetric but has purely imaginary eigenvalues. Thus, the coupled system is in the PT-symmetry broken phase. The border of the lasing phase 2 consists of the ST1 and ST2 lines and a section of the TH2 line. In this phase, ${\mathcal{H}}_{{\mathrm{ss}}}$ does not satisfy the PT symmetry, $PT{\mathcal{H}}_{{\mathrm{ss}}} \ne {\mathcal{H}}_{{\mathrm{ss}}}PT$. The coupled system possesses an unstable regime surrounded by the ST2 line and a section of the TH2 line. This regime actually corresponds to the PT-symmetry unbroken phase, where ${\mathcal{H}}\left( t \right)$ is PT symmetric and both fields exhibit an oscillatory behavior with a frequency of $\sim g_{\mathrm{C}}$. The rest regime of the $R - g_{\mathrm{C}}$ plane accounts for the no lasing phase, where the population inversion of the active particles cannot be achieved. The coupled system in different phases may be identified from the distinct behaviors of the photon numbers $n_{k = 1,2}$. In addition, two cavity outputs enable a direct measurement of the emission spectra from their beat note.

Fig. 4: Phase diagram of the macroscopic-sized open system.

The pumping rate $R$ and intercavity coupling strength $g_{\mathrm{C}}$ are tuned widely. The loss rate $\kappa _1$ of cavity 1 is chosen as the frequency unit in the plot. The whole $R - g_{\mathrm{C}}$ plane is divided into four regimes by four curves. Two threshold lines (TH1, dotted and TH2, dash-dotted) are determined by two sets of steady-state solutions of the coupled system. Two stability boundary lines (ST1, solid and ST2, dashed) are obtained from the linear stability analysis of the steady-state solutions. In the lasing phase 1, the steady-state Hamiltonian ${\mathcal{H}}_{{\mathrm{ss}}}$ possesses the PT symmetry but the coupled system is in the broken phase. In the lasing phase 2, ${\mathcal{H}}_{{\mathrm{ss}}}$ is non-PT symmetric. In the unstable regime, ${\mathcal{H}}\left( t \right)$ becomes PT symmetric and the coupled system is in the unbroken phase. In the rest regime, no lasing action occurs.

Microlaser

As the system’s size (measured by the number of particles and photons) is significantly reduced, the quantum effects (such as light’s particle nature and cavity quantum electrodynamics) become predominant. Our next study is dedicated to the PT symmetry of a microlaser (cavity 1) resonantly interacting with an empty cavity (cavity 2) as illustrated in Fig. 1b. The photon creation and annihilation operators for the cavity $k = 1,2$ are $a_k^\dagger$ and $a_k$, respectively. The microlaser consists of one active particle placed between two highly reflective mirrors. The energy-level structure of the particle involves four states $\left| {1,2,3,4} \rangle\right.$, whose energies are in an ascending order. The decay rate from $\left| i\rangle \right.$ (higher) to $\left| j \rangle\right.$ (lower) is $\gamma _{ij}$. An external laser beam resonantly drives the $\left| 1 \rangle\right. - \left| 4 \rangle\right.$ transition with a Rabi frequency ${\mathrm{{\Omega}}}$ and cavity 1 is resonantly coupled to the lasing $\left| 2 \rangle\right. - \left| 3\rangle \right.$ transition (frequency $\omega _0$) with a strength $g_{\mathrm{A}}$. Reducing the mode volume of cavity 1 may strongly enhance $g_{\mathrm{A}}$ so that only a few or even less than one photon can saturate the lasing transition, that is, $4g_{\mathrm{A}}^2/{\mathrm{{\Gamma}}}_{32}^2 \gg 1$ with ${\mathrm{{\Gamma}}}_{32} = \left( {\gamma _{32} + \gamma _{31} + \gamma _{21}} \right)/2$. Again, the photon loss rates of two cavities are $\kappa _1$ and $\kappa _2$, respectively, and $g_{\mathrm{C}}$ denotes the intercavity coupling strength. In what follows, we restrict ourselves to the system operating in the strong photon–particle coupling limit, that is, the lasing regime with $4g_{\mathrm{A}}^2/{\mathrm{{\Gamma}}}_{32}^2 \gg 1$ and $4g_{\mathrm{A}}^2/\kappa _1{\mathrm{{\Gamma}}}_{32} \gg 1$. We emphasize that such a one-particle laser is experimentally feasible by means of current optical techniques, where the active particle can be an ion²⁶ or a quantum dot³⁸. The dynamics of the coupled system is governed by the Lindblad master equation³⁹, which combines both the coherent particle–cavity and intercavity interactions and the dissipative processes of the particle and intracavity photons (Supplementary Note 2). We employ the Monte Carlo wavefunction method⁴⁰ to investigate the PT-symmetric properties of the system’s unique steady state⁴¹.

As depicted in Fig. 5a, the dependence of the steady-state photon numbers $n_{{\mathrm{ss}},k = 1,2} = \langle a_k^\dagger \left( t \right)a_k\left( t \right)\rangle_{t \to \infty }$ (here $a_k^\dagger \left( t \right)$ and $a_k\left( t \right)$ are the photon operators in the Heisenberg picture and $\langle\ldots\rangle _{t \to \infty }$ denotes the expectation value in the steady state) on the intercavity coupling strength $g_{\mathrm{C}}$ can be divided into four regimes, whose boundaries are found by the slope sign change of the $n_{{\mathrm{ss}},k = 1,2}$ vs. $g_{\mathrm{C}}$ curves. In the weak-$g_{\mathrm{C}}$ regime, $n_{{\mathrm{ss}},1}$ is higher than $n_{{\mathrm{ss}},2}$ and their difference ${\mathrm{{\Delta}}}n_{{\mathrm{ss}}} = n_{{\mathrm{ss}},1} - n_{{\mathrm{ss}},2}$ decreases towards zero as $g_{\mathrm{C}}$ is enhanced. Meanwhile, the photon number distributions of the two cavity fields tend to be the same (Fig. 5b). In the strong-$g_{\mathrm{C}}$ regime, the two cavity fields have similar photon numbers that roughly maintain a constant value as $g_{\mathrm{C}}$ grows. The photon distributions of the two cavity fields are almost the same and they apparently differ from the Poisson distribution. For a large enough $g_{\mathrm{C}}$, both $n_{{\mathrm{ss}},k = 1,2}$ degrade since the cavity-mode shifts induced by the intercavity interaction weaken the lasing action in cavity 1. Eventually, $n_{{\mathrm{ss}},k = 1,2}$ are suppressed to a near-zero value. Unlike the macroscopic counterpart, the microscopic system does not exhibit an unstable regime.

Fig. 5: Steady-state intracavity photon numbers of the microscopic-sized open system composed of a microlaser interacting with an empty optical cavity.

a Dependence of $n_{{\mathrm{ss}},k = 1,2}$ and the photon difference ${\mathrm{{\Delta}}}n_{{\mathrm{ss}}} = n_{{\mathrm{ss}},1} - n_{{\mathrm{ss}},2}$ on the intercavity coupling strength $g_{\mathrm{C}}$. Here, the subscript ss denotes the steady-state solutions and $k = 1,2$ represent the cavities 1 and 2, respectively. The loss rate $\kappa _1$ of cavity 1 is chosen as the frequency unit in the plot. Four regimes are presented according to the slope sign change of the $n_{{\mathrm{ss}},k = 1,2}$ vs. $g_{\mathrm{C}}$ curves. In the first regime, $n_{{\mathrm{ss}},k = 1,2}$ are apparently different and the coupled system is in the PT-symmetry broken phase. In the rest three regimes, ${\mathrm{{\Delta}}}n_{{\mathrm{ss}}}$ approximates zero and the coupled system is in the PT-symmetry unbroken phase. b Normalized photon distributions of two cavity fields for different $g_{\mathrm{C}}$ (histograms). The Poisson distributions based on the corresponding $n_{{\mathrm{ss}},1}$ (circles) and $n_{{\mathrm{ss}},2}$ (squares) are shown for comparison.

To map the steady-state solutions of the coupled system onto the time-independent Schrödinger-like Eq. (5), we write the cavity fields as ${\mathcal{A}}_{{\mathrm{ss}},k = 1,2} = \sqrt {n_{{\mathrm{ss}},k}} e^{{\mathrm{i}}\theta _{{\mathrm{ss}},k}}$ with the field phases $\theta _{{\mathrm{ss}},k}$ relative to that of the particle’s polarization (Supplementary Note 2). The diagonal element and eigenvalue of the shifted Hamiltonian ${\mathcal{H}}_{{\mathrm{ss}}}$ are then given by $\mu _{{\mathrm{ss}}} = ( {g_{\mathrm{C}}/2} )( {{\mathcal{A}}_{{\mathrm{ss}},1}/{\mathcal{A}}_{{\mathrm{ss}},2} - {\mathcal{A}}_{{\mathrm{ss}},2}/{\mathcal{A}}_{{\mathrm{ss}},1}})$ and $\lambda _{{\mathrm{ss}}} = ( {g_{\mathrm{C}}/2} )( {{\mathcal{A}}_{{\mathrm{ss}},1}/{\mathcal{A}}_{{\mathrm{ss}},2} + {\mathcal{A}}_{{\mathrm{ss}},2}/{\mathcal{A}}_{{\mathrm{ss}},1}})$, respectively. It should be noted that the expressions of $\mu _{{\mathrm{ss}}}$ and $\lambda _{{\mathrm{ss}}}$ in terms of ${\mathcal{A}}_{{\mathrm{ss}},k = 1,2}$ are also valid for the macroscopic coupled system. The numerical simulation results manifest $\theta _{{\mathrm{ss}},1} = {\uppi}/2$ and $\theta _{{\mathrm{ss}},2} = 0$ for an arbitrary $g_{\mathrm{C}}$. Consequently, $\mu _{{\mathrm{ss}}}$ is purely imaginary and ${\mathcal{H}}_{{\mathrm{ss}}}$ owns the PT symmetry, $PT{\mathcal{H}}_{{\mathrm{ss}}} = {\mathcal{H}}_{{\mathrm{ss}}}PT$. In the weak-$g_{\mathrm{C}}$ regime, $\lambda _{{\mathrm{ss}}}$ is purely imaginary since $n_{{\mathrm{ss}},1}$ differs from $n_{{\mathrm{ss}},2}$, that is, ${\mathrm{{\Delta}}}n_{{\mathrm{ss}}} \ne 0$. Hence, the coupled system is in the PT-symmetry broken phase (Fig. 5a). By contrast, $n_{{\mathrm{ss}},1}$ is almost equal to $n_{{\mathrm{ss}},2}$ for a large enough $g_{\mathrm{C}}$, that is, ${\mathrm{{\Delta}}}n_{{\mathrm{ss}}}\sim 0$, indicating that $\lambda _{{\mathrm{ss}}} \approx 0$ and the coupled system is in the unbroken phase.

The PT-symmetry breaking is accompanied by a change in the two cavity-field spectra $S_{k = 1,2}\left( \omega \right)$ (see “Methods”). When the coupled system is in the broken phase, for a small $g_{\mathrm{C}}$ both $S_{k = 1,2}\left( \omega \right)$ present only one spectral peak located at the resonance $\omega = \omega _0$. As $g_{\mathrm{C}}$ grows, the spectral peak in $S_1\left( \omega \right)$ is split into two due to the intercavity interaction while $S_2\left( \omega \right)$ is still single-peaked (Fig. 6a). The spectrum $S_2\left( \omega \right)$ starts to split when the coupled system approaches the phase transition boundary. Unlike the double-peaked $S_1\left( \omega \right)$, the two spectral peaks in $S_2\left( \omega \right)$ are unresolvable in principle since the interpeak separation is smaller than the peak linewidth (Fig. 6b). Interestingly, in the broken phase the peak linewidth of $S_1\left( \omega \right)$ always exceeds that of $S_2\left( \omega \right)$. In other words, the cavity field 2 has a temporal coherence superior to the cavity field 1, although the former entirely comes from the latter. As $g_{\mathrm{C}}$ is further increased, the coupled system enters the unbroken phase, where both $S_{k = 1,2}\left( \omega \right)$ exhibit a double-peaked profile. The two spectra have similar interpeak separations ($\sim 2g_{\mathrm{C}}$) and similar peak linewidths. For either $S_{k = 1,2}\left( \omega \right)$, the separation between two spectral peaks surpasses the peak linewidth, leading to two resolvable peaks. Therefore, the PT-symmetry breaking can be detected through the measurement of the lasing spectra. Moreover, we find that the cross-spectrum $S_{12}\left( \omega \right)$ between two cavity fields (see “Methods”) is almost the same as $S_2\left( \omega \right)$ as shown in Fig. 6a. That is, the cross-correlation between the two cavity fields is primarily determined by cavity field 2, whose coherence is greater than cavity field 1.

Fig. 6: Emission spectra of two cavity fields.

a Spectra $S_{k = 1,2}\left( \omega \right)$ and cross-spectrum $S_{12}\left( \omega \right)$ at several different intercavity coupling strengths $g_{\mathrm{C}}$. Here, $k = 1,2$, respectively, represent the cavities 1 and 2, $\omega$ denotes the angular frequency in the frequency domain, and $\omega _0$ corresponds to the central frequency of the laser transition. The loss rate $\kappa _1$ of cavity 1 is chosen as the frequency unit in the plot. b Interpeak separations of $S_{k = 1,2}\left( \omega \right)$ and $S_{12}\left( \omega \right)$ as a function of $g_{\mathrm{C}}$. Inset: Linewidths of the spectral peaks in $S_{k = 1,2}\left( \omega \right)$ and $S_{12}\left( \omega \right)$ vs. $g_{\mathrm{C}}$. The peak linewidths are evaluated by means of curve fitting (see “Methods”). The arrow shows the phase transition boundary, above which the interpeak separations exceed the linewidths of spectral peaks in both spectra $S_{k = 1,2}\left( \omega \right)$.

We are also interested in the second-order (intensity) autocorrelation functions $C_{k = 1,2}^{\left( 2 \right)}\left( \tau \right) = a_k^\dagger \left( t \right)a_k^\dagger \left( {t + \tau } \right)a_k\left( {t + \tau } \right)a_k\left( t \right)_{t \to \infty }/n_{{\mathrm{ss}},k}^2$ with a time difference $\tau$. Such detection can be performed by the well-known Hanbury Brown–Twiss setup⁴². The statistical characteristics of the photon emission from individual cavities are closely related to $C_{k = 1,2}^{\left( 2 \right)}\left( \tau \right)$ in the short-time-delay limit $\tau = 0$. As illustrated in Fig. 7a, both $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)$ are equal or higher than unity. Thus, the photon distributions of two cavity fields exhibit a Poisson or a super-Poissonian statistics (Fig. 5b), corresponding to the photon bunching effect. This is ascribed to the fact that the open system operates in the good-cavity limit (i.e., $\kappa _{k = 1,2} \ll \gamma _{32}$), where the ability of the cavities to accumulate the photons plays a notable role. One may expect a nonclassical behavior (i.e., photon antibunching/single-photon emission) of individual cavity fields when the cavity loss rates approximate to (see below) or much exceed the decay rates of the particle states (i.e., the bad-cavity limit, Supplementary Note 2). In this circumstance, one photon that is generated via the stimulated emission of the active particle may escape the cavities before the particle population is inverted again for the next stimulated emission event. The resulting photon distributions of individual cavity fields are characterized by a sub-Poissonian statistics. In addition, the single-photon emission can also be performed through the pulsed pump process⁴³ (Supplementary Note 2). When the coupled system is in the broken phase, $C_{k = 1,2}^{\left( 2 \right)}\left( \tau \right)$ gradually go up towards unity as $\tau$ is increased. By contrast, for the coupled system in the unbroken phase, the dependence of $C_{k = 1,2}^{\left( 2 \right)}\left( \tau \right)$ on $\tau$ displays a damped oscillatory behavior with an oscillation frequency $\sim 2g_{\mathrm{C}}$ (Fig. 7b).

Fig. 7: Second-order auto- and cross-correlation functions of intracavity light fields.

a Zero-time-difference intensity autocorrelation $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)$ and cross-correlation $C_{k = 12,21}^{\left( 2 \right)}\left( {\tau = 0} \right)$ vs. the intercavity coupling strength $g_{\mathrm{C}}$. Here, $k = 1,2$ represent the cavities 1 and 2, respectively, and $C_{12}^{\left( 2 \right)}\left( \tau \right) = a_2^\dagger \left( t \right)a_1^\dagger \left( {t + \tau } \right)a_1\left( {t + \tau } \right)a_2\left( t \right)_{t \to \infty }/n_{{\mathrm{ss}},1}n_{{\mathrm{ss}},2}$ and $C_{21}^{\left( 2 \right)}\left( \tau \right) = a_1^\dagger \left( t \right)a_2^\dagger \left( {t + \tau } \right)a_2\left( {t + \tau } \right)a_1\left( t \right)_{t \to \infty }/n_{{\mathrm{ss}},1}n_{{\mathrm{ss}},2}$. The subscript ss denotes the steady-state solutions. The loss rate $\kappa _1$ of cavity 1 is chosen as the frequency unit in the plot. The bunching effect corresponds to $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right) \ge 1$, while $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right) < 1$ denotes the antibunching. b Intensity autocorrelation $C_{k = 1,2}^{\left( 2 \right)}\left( \tau \right)$ and cross-correlation $C_{k = 12,21}^{\left( 2 \right)}\left( \tau \right)$ as a function of the time difference $\tau$ with $g_{\mathrm{C}} = 10\kappa _1$. All $C_{k = 1,2,12,21}^{\left( 2 \right)}\left( \tau \right)$ display a damped oscillatory behavior. c Steady-state photon numbers $n_{{\mathrm{ss}},k = 1,2}$, $C_{k = 1,2,12,21}^{\left( 2 \right)}\left( 0 \right)$, and the ratio $\chi = [ {C_{12}^{( 2 )}( 0 )} ]^2/[ {C_1^{( 2 )}( 0 )C_2^{( 2 )}( 0 )}]$ vs. $g_{\mathrm{C}}$ for the low-quality-factor optical cavities, where $\gamma _{41} = \gamma _{43} = \gamma _{31} = \gamma _{32} = \kappa _1$, $\gamma _{42} = 0.1\kappa _1$, $\gamma _{21} = 2\kappa _1$, $\kappa _2 = 2\kappa _1$, and ${\mathrm{{\Omega}}} = g_{\mathrm{A}} = 4\kappa _1$. Here, $\gamma _{ij}$ with $i,j = 1,2,3,4$ and $i > j$ corresponds to the decay rate of the particle from the $\left| i \rangle\right.$ to $\left| j \rangle\right.$ state, ${\mathrm{{\Omega}}}$ is the Rabi frequency of the pump light coupling to the particle’s $\left| 1 \rangle\right. - \left| 4 \rangle\right.$ transition, and $g_{\mathrm{A}}$ is the coupling strength between the cavity 1 and the laser $\left| 2\rangle \right. - \left| 3\rangle \right.$ transition. The coupled system still operates in the strong photon–particle coupling limit, that is, $4g_{\mathrm{A}}^2/{\mathrm{{\Gamma}}}_{32}^2 \gg 1$ and $4g_{\mathrm{A}}^2/\kappa _1{\mathrm{{\Gamma}}}_{32} \gg 1$ with ${\mathrm{{\Gamma}}}_{32} = \left( {\gamma _{32} + \gamma _{31} + \gamma _{21}} \right)/2$. The gray shade denotes the regime of the nonclassical photon-pair generation with $\chi > 1$, that is, the violation of the Cauchy–Schwarz inequality.

In addition, one may examine the intensity cross-correlation functions $C_{12}^{\left( 2 \right)}\left( \tau \right) = a_2^\dagger \left( t \right)a_1^\dagger \left( {t + \tau } \right)a_1\left( {t + \tau } \right)a_2\left( t \right)_{t \to \infty }/n_{{\mathrm{ss}},1}n_{{\mathrm{ss}},2}$ and $C_{21}^{\left( 2 \right)}\left( \tau \right) = a_1^\dagger \left( t \right)a_2^\dagger \left( {t + \tau } \right)a_2\left( {t + \tau } \right)a_1\left( t \right)_{t \to \infty }/n_{{\mathrm{ss}},1}n_{{\mathrm{ss}},2}$, which are measured via the coincidence counting interferometry as shown in Fig. 1b. We have $C_{12}^{\left( 2 \right)}\left( 0 \right) = C_{21}^{\left( 2 \right)}\left( 0 \right)$ in the limit of $\tau \sim 0$. Both $C_{k = 12,21}^{\left( 2 \right)}\left( 0 \right)$ are equal to unity for the cavity fields in the coherent states (i.e., the eigenstates of $a_{1,2}$). When $C_{k = 12,21}^{\left( 2 \right)}\left( 0 \right) < 1$, two cavity fields are anticorrelated. Recently, the anticorrelation between coupled nanolasers has be observed⁴⁴. It is seen from Fig. 7a that $C_{k = 12,21}^{\left( 2 \right)}\left( 0 \right)$ of the coupled system go down below unity as the coupling strength $g_C$ is increased. That is, two cavities are unlikely to emit the photons at the same time, even though each cavity emits the photons in bunches ($C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right) \ge 1$). This is because, for instance, after cavity 2 emits a photon, a portion of the photons inside cavity 1 is consumed to compensate the loss of the cavity field 2, causing cavity 1 hardly emits a photon. A large $g_{\mathrm{C}}$ facilitates such a process. Interestingly, the anticorrelation between two cavity fields happens before the occurrence of the PT-symmetry breaking. Thus, the PT symmetry does not account for all the properties of the coupled system. Both $C_{k = 12,21}^{\left( 2 \right)}\left( \tau \right)$ undergo the damped oscillations at a frequency $\sim 2g_{\mathrm{C}}$ and approach unity as $\tau$ goes to infinity, but their behaviors are still slightly different because of the asymmetry of the physical system (Fig. 7b). Using the bad cavities or the pulsed pump approach, one may obtain both strong photon antibunching of individual cavity fields $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)\sim 0$ and strong anticorrelation between two cavity fields $C_{k = 12,21}^{\left( 2 \right)}\left( 0 \right)\sim 0$ (Supplementary Note 2).

We further consider the nonclassical photon-pair generation that is characterized by the violation of the Cauchy–Schwarz inequality⁴⁵ $\chi \equiv [ {C_{12}^{( 2 )}( 0 )} ]^2/[ {C_1^{( 2 )}( 0 )C_2^{( 2 )}( 0 )} ] \le 1$. As illustrated in Fig. 7a, $\chi$ is always lower than unity in the good-cavity limit, that is, the absence of the nonclassical feature. Increasing the cavity loss rates $\kappa _{k = 1,2}$ may suppress both $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)$, giving rise to the potential of violating the inequality. Although large $\kappa _{1,2}$ reduce the cavity-field intensities $n_{{\mathrm{ss}},k = 1,2}$ (Fig. 7c), the coupled system still operates in the lasing regime when the strong particle–cavity coupling limit (i.e., $4g_{\mathrm{A}}^2/{\mathrm{{\Gamma}}}_{32}^2 \gg 1$ and $4g_{\mathrm{A}}^2/\kappa _1{\mathrm{{\Gamma}}}_{32} \gg 1$) is reached. Figure 7c illustrates that in the weak-$g_{\mathrm{C}}$ regime, the ratio $C_{12}^{\left( 2 \right)}\left( 0 \right)/C_1^{\left( 2 \right)}\left( 0 \right)$ is larger than the ratio $C_2^{\left( 2 \right)}\left( 0 \right)/C_{12}^{\left( 2 \right)}\left( 0 \right)$, resulting in χ > 1, that is, the nonclassical photon-pair generation. Meanwhile, for an appropriate $g_{\mathrm{C}}$ both $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)$ may be below unity, that is, the nonclassical photon emission of individual cavity fields. By contrast, when $g_{\mathrm{C}} > \kappa _1$, $C_{12}^{\left( 2 \right)}\left( 0 \right)$ is lower than both $C_{k = 1,2}^{\left( 2 \right)}\left( 0 \right)$ and the inequality $\chi \le 1$ becomes satisfied again.

In summary, our work explores fundamental properties of PT-symmetric optics in the lasing regime, where, to the best of our knowledge, the microscopic coupled structures have not been accessed before. We extend the PT-symmetric optics from the weak to the strong particle–cavity coupling limit, where the particle polarization cannot be adiabatically eliminated. The resulting phase diagrams differ from the usual PT-symmetric optical schemes based on the rate-equation model^{16,17,18,19,20}. The phase boundaries of the macroscopic-sized system are well defined by the lasing thresholds and the stability analysis of the steady-state solutions. The emission spectra can be employed to detect the PT-symmetric properties, avoiding the extra noise sources caused by the technical issues in the transmission spectrum measurement. By contrast, the interphase boundary becomes fuzzy as the system’s size is significantly reduced to the microscopic scale. The intensity auto- and cross-correlation functions of the microscopic-sized system with appropriate cavity loss rates illustrate the nonclassical photon emission of individual cavities and the nonclassical photon-pair generation.

Conclusion

Recent developments in atomic physics, microcavity technology, and nanophotonics will allow the predictions obtained in this paper to be tested. The macroscopic lasers have been demonstrated by high-$Q$ optical cavities filled with dilute atomic gases^{21,22,23,24,25} and fluorescent dye molecules³¹, ion-doped PhC cavities^32,33, and dye-doped polymer resonators⁴⁶. The intercavity coupling can be either in a direct manner (i.e., the spatial overlap of two cavity modes) or mediated via another optical device. The experimentally achieved $g_{\mathrm{C}}$, for example, between two PhC cavities exceeds 10² GHz¹². In contrast, the microlasers can be implemented via one quantum dot embedded in a nanoscale PhC/semiconductor cavity^38,47. The mode volume of a PhC nanocavity is extremely small, ~10⁻² μm³, resulting in a large $g_{\mathrm{A}}$ of ~10 GHz³⁸. Also, the microlaser structure may consist of one ion/molecule and a WGM microcavity³⁵, where the localized surface plasmon resonance of metal nanoparticles is utilized as a solution to achieve the strong particle–cavity coupling^48,49. Moreover, our study is potentially extended to coupled systems involving multi-energy-level particles⁵⁰ and particles with long-range interactions⁵¹.

The PT-symmetric lasing scheme may be applied for sensing and gyroscope applications^6,7,8,52. The spectral sensitivity of a modified non-Hermitian optical system to a small change ${\mathrm{{\Delta}}}g_{\mathrm{C}}$ of the intercavity coupling $g_{\mathrm{C}}$ scales as $\sqrt {{\mathrm{{\Delta}}}g_{\mathrm{C}}}$ around the EP⁶, exceeding the sensitivity around the normal diabolic point. For our macroscopic coupled system, we find that the changes of the photon numbers $n_{{\mathrm{ss}},k = 1,2}$ are proportional to ${\mathrm{{\Delta}}}g_{\mathrm{C}}$ around the phase 1–phase 2 transition point. However, due to the simulation restriction, we are unable to confirm if the dependence of the spectral splitting (see Fig. 2c) on ${\mathrm{{\Delta}}}g_{\mathrm{C}}$ follows the square root law around the phase transition point. In practice, our laser system facilitates this spectrum measurement directly from the beat note between two cavity outputs. In comparison, for the microscopic-sized system the small numbers $n_{{\mathrm{ss}},k = 1,2}$ challenge the detection of ${\mathrm{{\Delta}}}g_{\mathrm{C}}$. Nevertheless, since the particle–cavity interaction depends strongly on the square root of the number $N$ of the particles located inside the cavity⁵³, this can be utilized to detect the particle number with a sensitivity that scales as $1/\sqrt N$ and is maximized when $N = 1$, that is, the single-particle level.

Methods

Lasing spectra of macroscopic-sized system

The cavity-field spectra of the classical optical system may be obtained by numerically solving the $c$-number Langevin equations listed in Supplementary Note 1. For simplicity, we assume the open system operates at zero temperature and the Langevin forces related to the cavity fields are eliminated. The laser spectral linewidth is primarily caused by the fluctuations in the macroscopic polarization ${\mathcal{M}}\left( t \right)$ of the active particles. One may only take into account its associated Langevin force ${\mathcal{F}}_{\mathcal{M}}\left( t \right)$ and omit the Langevin forces exerting on other particle variables. The Langevin force ${\mathcal{F}}_{\mathcal{M}}\left( t \right)$ is characterized by the correlation functions $\langle{\mathcal{F}}_{\mathcal{M}}\left( t \right)\rangle = 0$, $\langle{\mathcal{F}}_{\mathcal{M}}\left( t \right){\mathcal{F}}_{\mathcal{M}}\left( {t^{\prime}} \right)\rangle = 2{\mathcal{D}}\left( {{\mathcal{M}},{\mathcal{M}}} \right)\delta \left( {t - t^{\prime}} \right)$, and $\langle{\mathcal{F}}_{\mathcal{M}}^ \ast( t ){\mathcal{F}}_{\mathcal{M}}( {t^{\prime}} )\rangle = 2{\mathcal{D}}( {{\mathcal{M}}^ \ast ,{\mathcal{M}}})\delta ( {t - t^{\prime}})$. The delta function illustrates the white noise force. The diffusion coefficients ${\mathcal{D}}\left( {{\mathcal{M}},{\mathcal{M}}} \right)$ and ${\mathcal{D}}( {{\mathcal{M}}^ \ast ,{\mathcal{M}}})$ are related to the steady-state solutions of the open system (Supplementary Note 1). The cavity fields ${\mathcal{A}}_{k = 1,2}\left( t \right)$ are simulated based on the Langevin equations combined with the numerically generated Langevin force ${\mathcal{F}}_{\mathcal{M}}\left( t \right)$. The cavity-field spectra are then given by $S_{k = 1,2}\left( \omega \right) \propto \left| {\mathop {\smallint }\nolimits {\mathcal{A}}_k\left( t \right){\mathrm{e}}^{ - {\mathrm{i}}\omega t}{\mathrm{d}}t} \right|^2$. The curve fitting in Figs. 2c and 3c is performed according to the Lorentzian function $L\left( \omega \right)$ or $\left[ {L\left( {\omega - {\Delta}} \right) + L\left( {\omega + {\Delta}} \right)} \right]/2$ with a frequency shift Δ. The separation of the spectrum splitting reads 2Δ.

Emission spectra of microscopic-sized open system

The emission spectra of two cavity fields are derived from the Fourier transform of the autocorrelation functions $C_{k = 1,2}^{\left( 1 \right)}\left( \tau \right) = \langle a_k^\dagger \left( {t + \tau } \right)a_k\left( t \right)\rangle_{t \to \infty }/n_{ss,k}$ with respect to the time delay $\tau$, that is, $S_{k = 1,2}( \omega ) \propto \mathop {\smallint }\nolimits {\mathrm{Re}} [ {C_k^{( 1 )}( \tau )} ]{\mathrm{e}}^{ - {\mathrm{i}}\omega \tau }{\mathrm{d}}\tau$. The two-time correlation functions $C_{k = 1,2}^{\left( 1 \right)}\left( \tau \right)$ can be computed by using the Monte Carlo wavefunction method⁴⁰ to simulate the Lindblad master equation of the open system. The cross-correlation between two cavity fields takes the form $C_{12}^{\left( 1 \right)}\left( \tau \right) = [\langle {a_1^\dagger \left( {t + \tau } \right)a_2\left( t \right)\rangle_{t \to \infty }{\mathrm{e}}^{ - {\mathrm{i}}\varphi } + \langle a_2^\dagger \left( {t + \tau } \right)a_1\left( t \right)\rangle_{t \to \infty }{\mathrm{e}}^{{\mathrm{i}}\varphi }} ]/\sqrt {n_{{\mathrm{ss}},1}n_{{\mathrm{ss}},2}}$ with an extra phase difference $\varphi$ of cavity field 2 relative to cavity field 1. The corresponding cross-spectrum reads $S_{12}\left( \omega \right) \propto \mathop {\smallint }\nolimits {\mathrm{Re}} [ {C_{12}^{\left( 1 \right)}\left( \tau \right)} ]{\mathrm{e}}^{ - {\mathrm{i}}\omega \tau }{\mathrm{d}}\tau$. Here we set $\varphi = {\uppi}/2$ due to the steady-state phase difference ${\Delta}\theta _{{\mathrm{ss}},1} - {\Delta}\theta _{{\mathrm{ss}},2} = {\uppi}/2$ between two cavity fields. To evaluate the linewidths and frequency shifts of the spectra $S_{k = 1,2,12}\left( \omega \right)$, one may fit the exponential decay function $Ae^{ - \gamma \tau /2}\cos \left( {{\mathrm{{\Delta}}}\tau + \theta } \right)$ with an amplitude $A$, a decay constant $\gamma$, an oscillation frequency ${\mathrm{{\Delta}}}$ and a phase bias $\theta$ to the correlation functions $C_{k = 1,2,12}^{\left( 1 \right)}\left( \tau \right)$. The linewidth of the peak(s) in a spectrum is determined by $\gamma$. Due to the nonzero $\theta$, the separation between two peaks in a double-peaked spectrum differs from $2{\mathrm{{\Delta}}}$, especially for the coupled system in the broken phase. Thus, the interpeak separation is computed directly from the double-peaked spectrum.