Introduction

Quantum states of light provide an exciting platform for observing and controlling matter beyond what is possible classically1,2,3,4. Quantum states are very sensitive to the external environment, which makes them useful probes of matter. Quantum features of light have long been used in metrology and quantum information5,6 while lately there has been a growing activity in utilizing them in spectroscopic applications7,8. Interferometry offers robust detection schemes of quantum light. In this paper, we present a novel spectroscopy based on the Hong-Ou-Mandel (HOM)9 two-photon interferometric setup. Observables measured by the interference of two waves depend on two times separated by a delay Δ which can be controlled by the propagation path difference of the mixed waves. The unified picture of second-order and fourth-order interferences in a single interferometer has been demonstrated in ref. 10. Previous works attempted either to utilize HOM-like measurements to address properties of the beam splitters or the individual emitters11 or utilize four-wave mixing for the quantum light generation12 and characterization13.

Interferometric signals can be recast in terms of moments of the field operators posterior to the interaction with the matter, thereby revealing its statistics. The signal-field operator (see “Methods” and Supplementary Note 1) is given by14

$${\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},{\mathbf{t}}} \right) = - i\omega _s\hat V\left( {{\mathbf{r}},t} \right),$$
(1)

Where ωs is the signal mode frequency and \(\hat V\) is the matter dipole operator. The interferometric setup naturally gives rise to two characteristic timescales and respective length scales. First, the response interval τR in which light-matter interaction occurs. It is determined by the pulse envelope, the spatial dimension of the sample, and the response time. Second, is the pulse relative delay interval δT determined by the interference region governed by the interferometer dimensions. Here, we consider the field-matter interaction region to be localized compared to the spatial dimensions of the interferometer. We further consider a sequence of ultrafast coherent excitation pulses—which are classical for all practical purposes—followed by an interaction with the quantum state of light. The interferometer operation mode is shown in Fig. 1: when the pulse interval cδT and the maximal response interval of the sample cτR, are smaller than the free propagation distance between the sample and the interference-detection location Lp (L* ≪ Lp) where L* := cmax{τR’ δT}—the measured response functions are classical. The response in this regime is highly localized temporally and immediately after the pulse interacts with the sample, the matter degrees of freedom can be traced out. The excitation and deexcitation period is dominated by the duration of the narrowband envelope of the quantum field given by cτR combined with the pulse delay interval cδT. The maximal duration of this interval is defined by L* which is smaller than a few hundred micrometers even for a picosecond pulse which is well within the narrowband region. For example, for a transform-limited Gaussian pulse with central wavelength λc = 1064 nm and pulse duration Δt = 2 ps which occupies cτR ≈ 600 μm. Finally, the interferometer length scale denoted Lp specifies the free propagation distance between the incident beams, the beamsplitter, and the detector. Typical interferometer length is in the order of few centimeters which justifies the separation of timescales—considering the interaction interval to be localized around the sample compared with Lp. Moreover, the Rayleigh distance is typically a few meters in this setup, thus one can consider the propagation as unidirectional for all practical purposes. For a femtosecond pulse cδT ∝ 10−1 μm while for a traditional interferometer Lp is in the order of centimeters. In the following we consider short pulses, so that (L* ≪ Lp). Trace w.r.t. matter results in the nth order polarization in the external field \(P^{\left( n \right)}\left( t \right) \equiv \hat V\left( t \right)_{\left\{ n \right\}}\) (details are given below). This polarization serves as a source for the signal field. This regime fits experimental setups involving ultrafast pulses (δT ≤ 1 ps). In the opposite regime, cτR’ cδT ≫ Lp, the pulse is long enough to create ambiguity in the order of interactions and the arrival of the relatively delayed photons (see Supplementary Notes 2–4 for detailed derivations of this regime). One cannot then trace the matter degrees of freedom prior to the measurement which gives rise to different observables.

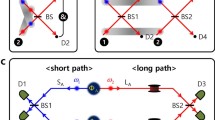
Fig. 1: Interferometric spectroscopy setup.
figure 1

Hong-Ou-Mandel interferometer. A pump beam propagates through a χ(2) nonlinear crystal. The interaction between field modes mediated through the crystal induces entanglement between two well separated beams of different polarization produced by spontaneous parametric down conversion. One beam interacts with a sample (inset I), while the other propagates in an empty arm. The two beams are finally combined on a beamsplitter (BS) (inset II), and collected in two detectors Da and Db. Insets I and II are specified in more detail in Figs. 3 and 4, respectively.

Full size image

In the present work, we combined the interferometric detection (HOM) with wave mixing that involves both classical and quantum light beams to address more complex nonlinear optical processes and the corresponding components of the nonclassical response function. We investigate how the quantum state of light and its statistics are modified by interaction with matter. In particular, we address the following two issues of the quantum nonlinear interferometric spectroscopy. The first issue is regarding the nature of the change of the quantum state and its statistics. The second point investigates the details of the matter information that can be deduced from the change in the statistics of the field. These questions are explored by using an interferometric setup traditionally used to study quantum states of light and now applied for investigation of the matter degrees of freedom via extraction of the matter response functions. We therefore focus on accuracy enhancement of such responses and their deviations from classical susceptibilities.

Results and discussion

The proposed experiment combines several conventionally used optical techniques such as four-wave mixing, beam splitting, and Hong-Ou-Mandel (HOM) interferometer, and three-photon absorption spectroscopy. In the following sections, we present each technique independently highlighting the main principle and the underlying theoretical model that will be used to describe each part of the setup. We finally combine both techniques in the setup shown in Fig. 2a and discuss the resulting HOM spectroscopic measurements. In the experimental setup the three classical light beams are combined with the quantum light pulse produced by the parametric down conversion (independently from the classical three pulses). The corresponding level scheme is shown in Fig. 2b. The main goal of the proposed measurement is to use interferometric (HOM-like) detection to investigate the χ(3) nonlinear susceptibility that combines an absorption of the three classical fields and the transmission of one quantum field shown in Fig. 2c. The corresponding Feynman diagram and HOM signal are shown in Fig. 2d, e, respectively. Unlike the Kerr process which requires high-intensity laser pulses to produce third-order nonlinear response, here we deal with resonant absorption of each of the light beams participating in the four-wave mixing. This nonlinear process is the main focus of our study.

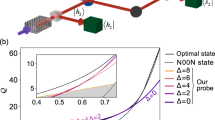
Fig. 2: Hong-Ou-Mandel (HOM) interference signal.
figure 2

An illustration of the variation of the coincidence probability with the optical delay Δ. a Level scheme of the model system. b Experimental setup based on HOM interferometer combined with four-wave mixing signal. c Its transmission function \(T(\omega ) \equiv 1 - iA_0\chi ^{(3)}(\omega )\) (real part—orange line, imaginary part—blue line) Vs the scanned frequency ω3 at fixed ω1 and ω2. The third-order susceptibility for a multi-level system is computed following ref. 9. d Schematic diagram representing the main contribution of the third-order susceptibility. e Variation of the HOM coincidence counting rates with the optical delay (without matter—blue line, with matter—orange line).

Full size image

The general third-order nonlinear optical process generates various signals that are well studied in classical light spectroscopy: optical pump-probe, Raman, fluorescence, transient grating, photon echo, and others. Four-wave mixing (FWM) signals play an important role as it allows to have additional control over the field-matter interactions via spatial phase matching. The typical FWM setup shown in Fig. 3 where three beams interacting with the material sample generate a fourth beam propagating in the direction governed by one of the eight possible phase-matching conditions. The response functions are obtained by tracing over the matter degrees of freedom. The state of the outgoing field in Fig. 3 is given by tracing Eq. (1) over the matter degrees of freedom \({\hat{\mathbf{E}}}_a^{\left( + \right)}\left( t \right) \to {\hat{\mathbf{E}}}_s^{\left( + \right)}\left( t \right)\),

$${\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},t} \right) = - i\omega _s\sqrt {\frac{{\hbar \omega _s}}{{2\pi }}} Nf\left( {{\Delta} k} \right){\int} {d\omega \chi ^{\left( 3 \right)}\left( \omega \right)\hat a\left( \omega \right)e^{ - i\omega t},}$$
(2)

where \(\chi ^{\left( 3 \right)}\left( \omega \right) \equiv \chi ^{\left( 3 \right)}\left( { - \omega ;\omega _3,\omega _2,\omega _1} \right)\) is the third-order susceptibility. We have omitted the three classical incoming wave frequencies for brevity. The matter is modeled by a collection of N homogeneously distributed point-like molecular dipoles at random positions rα. Adopting the multipolar coupling Hamiltonian following with rotational averaging we obtain

$$\hat V\left( {r,t} \right)_{\left\{ n \right\}} = \mathop {\sum}\nolimits_{\alpha = 1}^N {\delta \left( {{\mathbf{r}} - {\mathbf{r}}_\alpha } \right)\hat V\left( t \right)_{\left\{ n \right\}}e^{i{\mathbf{k}}_{\left\{ n \right\}}{\mathbf{r}}}.}$$
(3)

Here {n} denotes averaging with respect to the nth order density operator due to n interacting fields one of which is the photon with the entangled noninteracting counterpart. In this calculation, each of the incoming modes interacts with a single molecule. \(f\left( {{\Delta} \mathbf{k}} \right) = \frac{1}{N}\mathop {\sum}\nolimits_\alpha {e^{i{\Delta} \mathbf{k}{\mathbf{r}}_\alpha }}\) is a geometrical factor that carries the information regarding the distribution of molecules which gives rise to the phase-matching condition when Δk = 0 = k{n}−ks and \({\mathbf{k}}_{\left\{ n \right\}} = \mathop {\sum}\nolimits_{i = 1}^3 { \pm {\mathbf{k}}_i}\) where ks is the wavevector of the entangled photon containing the 23 phase-matching directions15. Note that f(0) = 1.

Fig. 3: Four-wave mixing scheme.
figure 3

Inset I in Fig. 1 is shown for a four-wave mixing process. Three incoming waves k1, k2, k3 interact with matter. The fourth ks mode is the detected signal in the direction dictated by the phase-matching factor f(Δk) introduced in Eq. (2).

Full size image

The Hong-Ou-Mandel interferometric signal

We next turn to the HOM two-photon interferometer in the presence of matter. The electric field is transformed by the relatively displaced beamsplitter (BS) depicted in Fig. 4 according to

$$\left( {\begin{array}{*{20}{c}} {{\hat{\mathbf{E}}}_{a\prime }^{\left( + \right)}\left( \omega \right)} \\ {{\hat{\mathbf{E}}}_{b\prime }^{\left( + \right)}\left( \omega \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\sqrt T } & {i\sqrt R e^{i\omega {\Delta} }} \\ {i\sqrt R e^{ - i\omega {\Delta} }} & {\sqrt T } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{\hat{\mathbf{E}}}_a^{\left( + \right)}\left( \omega \right)} \\ {{\hat{\mathbf{E}}}_b^{\left( + \right)}\left( \omega \right)} \end{array}} \right),$$
(4)

where the linear phase results in the ±Δ relative time delay, corresponding to the ±cΔ displacement of the BS. \(\sqrt T\) and \(\sqrt R\) are the transmission and reflection coefficients. We focus on the photon coincidence signal depicted in Fig. 1 given by a joint probability to detect one photon in Da and one photon in Db separated by delay τ given by

$${\cal{N}}P_{ab}\left( \tau \right) = \left\langle {\hat E_{a^\prime ,R}^{\left( - \right)}\left( t \right)\hat E_{b^\prime ,R}^{\left( - \right)}\left( {t + \tau } \right)\hat E_{b^\prime ,L}^{\left( + \right)}\left( {t + \tau } \right)\hat E_{a^\prime ,L}^{\left( + \right)}\left( t \right)} \right\rangle ,$$
(5)

where \({\cal{N}}\) is a normalization factor. We employ the superoperator notation, OLA = OA and ORA = AO, the superoperator O± represents an anti/commutator O±A = OA ± AO. Note that the superoperator time ordering Ƭ, which is an operator in Liouville space is different from the standard Glauber’s normally ordered operators7,8. The plus-minus and the left-right superoperators are linked by a linear transformation. Below we focus on a narrowband pump. Extension to a broadband pump is outlined in Supplementary Note 2.

Fig. 4: The beamsplitter.
figure 4

BS of inset II of Fig. 1 is shown with more details. The BS described in Eq. (4), generates a superposition of the incoming fields (plane subscripts) in its output (primed subscripts).

Full size image

The narrowband HOM spectrometer

In their seminal paper, HOM have used the narrowband wavefunction (see Eq. (16) and “Methods”). Following this procedure in path ‘a’ (top branch of the interferometer), a sample composed of many molecules is placed, and the signal is given by the four-wave mixing setup depicted in Fig. 3.

We focus on the L* ≪ Lp regime, where the spatial extent of the photon wavepacket after the interaction is small compared to the dimensions of the interferometer. Calculating the coincidence count according to Eq. (5) using Eqs. (2) and (15) we obtain,

$$P_{ab}\left( {\tau ,{\Delta} ;\left\{ \omega \right\}_n} \right) = P_0\left\{ \begin{array}{l}T^2\left| {C\left( \tau \right)|^2 + R^2} \right|C\left( {2{\Delta} - \tau } \right)|^2\\ - RT[C^ \ast \left( \tau \right)C\left( {2{\Delta} - \tau } \right)e^{ - i\omega _p\left( {\tau - {\Delta} } \right)} + c.c.]\end{array} \right\}.$$
(6)

Here the convoluted response is given by the functional C(τ) = G(τ)*χ(3)(τ), where \(G\left( \tau \right) = \left( {2\pi } \right)^{ - \frac{1}{2}}{\int} {d\omega {\Phi} \left( {\omega ,\omega _p - \omega } \right)e^{ - i\omega \tau },}\) where the two-photon wavefunction amplitude \({\Phi} \left( {\omega _a,\omega _b} \right)\) is given by Eq. (15) (see “Methods”); \(\chi ^{(3)}\left( \tau \right) = \left( {2\pi } \right)^{ - \frac{1}{2}}{\int} {d\omega \chi ^{(3)}\left( \omega \right)e^{ - i\omega \tau }}\) and \(\left\{ \omega \right\}_3 = \omega _1,\omega _2,\omega _3\) are the frequencies of the three classical waves. The pre-factor containing the central frequency and the setup geometry is given by \(P_0 = {\cal{N}}^{ - 1/2}(N\hbar \omega _0^2)^2|f\left( {{\Delta} k} \right)|^2\). In the absence of matter, χ(t) = δ(t) and we recover the HOM interference9 signal. In that case, the extra phase factor that appears in the second term in Eq. (6) can be shifted at the frequency integration by ω → ω + ωp/2. When the material sample is added, a reference frequency is set. This can be compensated by equivalently translated matter response. When the coincidence counting is not temporally gated, we obtain the signal by integration over τ,

$$P_{ab}\left( {{\Delta} ,\{ \omega \} _n} \right) = n_0 - v{\int} {d\tau \left\{ {C^ \ast \left( {{\Delta} + \tau } \right)C\left( {{\Delta} - \tau } \right)e^{ - i\omega _p\tau } + c.c.} \right\}.}$$
(7)

where \(n_0 = P_0\left( {R^2 + T^2} \right){\int} {d\tau |C(\tau )|^2}\), and v = P0 = P0RT. For large BS displacement cΔ, the overlap term—the second term in the R.H.S. of Eq. (7)—vanishes due to diminishing correlations of the relatively shifted response. It assumes a Wigner function form in the {Δ,ωp} space. As Δ is reduced, the overlap term increases, introducing the hallmark dip in the HOM interference pattern. A material sample added in one of the pathways affects the overlap term. Matter information is revealed in Eq. (7) by the variation of the HOM dip with the convoluted response C(τ) Wigner function as illustrated in Fig. 2e. Note, that the response function C(τ) is calculated using three classical fields followed by a single-photon field in the last interaction. While it is not unusual that quantum-enhanced performance is dramatically eroded by the loss of a single photon, this is not the case here. Several noise sources can be considered such as losses associated with single-photon sources, non-phase-matched contributions, and imperfect transmission and detection efficiency. First, the proposed setup in the single-photon regime allows overcoming the noise because of the photon correlation measurement. The classical incoming fields contain a large number of photons and are thus insensitive to losses compared to other classical technique. When the single-photon contribution has losses, the signal vanishes due to violation of the phase-matching due to momentum conservation. Second, the improved performance is attributed to the nonclassical correlations between the photon pair, not from their Fock-state characteristics. Contributions to such losses can originate from non-phase-matched signals, like spontaneous emission adding vacuum fluctuations to the transmitted beams. Third, losses occurring after the mixing can be modeled by a beamsplitter with an empty port16. Recent interferometry: Experiments in the four-wave mixing setup performed in a multiphoton regime17 indicate the reduction of quantum correlations is proportional to the square of the transmission ratios of the light beam intensities that characterize such losses. Single-photon experiments have substantially lower transmission ratios and are therefore robust against such losses. Finally, it has been shown that similar biphoton spectroscopy measurements are robust against the external noise at the detection stage such as background thermal radiation18, even under the signal-to-noise ratio reaches 1/30.

Interferometric detection of χ (3)

We now turn to the setup depicted in Fig. 2a. The molecule is modeled by a four-level system {g, e1, e2, f} with transition energies \(\omega _{e_1g} = E_{e_1} - E_g = 3\,{\mathrm{eV}}\), \(\omega _{e_2e_1} = 2\,{\mathrm{eV}}\), \(\omega _{fe_2} = 1\,{\mathrm{eV}}\). It undergoes three interactions with classical light pulses with controlled delays, the fourth-interaction is taken to be one photon produced by a parametric down-converted shown in Fig. 2a. The signal with phase matching at ks = ka + kb + kc can be generated in the four electronic state system. One can surely select another phase-matching direction, out of the eight possible ones. Each direction contains a different type of material information governed by the set of pathways containing in the corresponding χ(3) nonlinear susceptibility. The third-order nonlinear susceptibility is calculated using perturbative field-matter interactions according to the diagram in Fig. 2d. Following the general approach outlined in chapter six of ref. 19. We obtain:

$$\begin{array}{l} \chi ^{\left( 3 \right)}\left( { - \omega ;\omega _c,\omega _b,\omega _a} \right) \\ \quad= \frac{{ - \mu _{fe_2}\mu _{e_2e_1}\mu _{e_1g}}}{{(\omega _a + \omega _b + \omega _c - \omega _{fg} + i\gamma _{fg})(\omega _a + \omega _b - \omega _{e_2g} + i\gamma _{e_2g})(\omega _a - \omega _{e_1g} + i\gamma _{e_1g})}},\end{array}$$
(8)

where ω = ωa + ωb + ωc implies energy conservation and μij are transition dipole moments. The nonlinear susceptibility contains one-, two-, and three-photon resonances determined by the transition frequencies ωij and dephasing rates (linewidth) γij, i, j = g, e1, e2, f.

Figure 2e compares the HOM signal Pc(Δ) with and without matter. Without matter, the spectrum shows the well-known HOM dip. We consider three classical beams with central frequencies matching the \(\omega _{e_1g}\), \(\omega _{e_2e_1}\), and \(\omega _{fe_2}\). Here ωmn = Em − En is the transition frequency for n→m. We assume that the matter-induced modulation of the HOM spectrum measures the susceptibility χ(3)(−ω; ω3, ω2, ω1) obtained by scanning ω3 while ω1 and ω2 are fixed. The main contribution to χ(3) is represented by the ladder diagram shown in Fig. 2d. The sample breaks the time-reversal symmetry P(τ) = P(−τ) possessed by the bare HOM dip. Such symmetry is a consequence of the exchange symmetry in the twin-photon wavefunction Φ(ω1, ω2) = Φ(ω2, ω1). By modulating one arm of the twin-photon, the interaction with matter breaks the exchange symmetry. When absorption can be neglected, the matter acts as a frequency-dependent phase shifter \(T(\omega ) \equiv e^{i\theta (\omega )}\), the optical delay in the idler beam can compensate the modulation if Δ and θ have the same sign, or further enhance the relative phase difference between the two beams.

The measurement resolution can be controlled by photon entanglement. Figure 5 compares the HOM signal using a nonentangled photon pair (a, b) and highly entangled twin photons (c, d). The two-photon wavefunctions in panels a and c, and the corresponding HOM signals, are shown in panels b and d. The coincidence HOM measurement can reveal the energies and lifetimes of the four electronic levels {g, e1, e2, f} along with the transition dipoles between the states and relevant coherence dephasing rates. For instance, the f-g coherence dephasing is a crucial parameter that determines the temporal resolution of the coincidence measurement and strongly depends on the state of light. The signal in Fig. 5 is computed by scanning the pump frequency impinging the nonlinear crystal. As shown, the central feature arises at \(\frac{{\omega _p}}{2} = 6\,{\mathrm{eV}}\) which matches the transition frequency ωfg. The decay of the signal comes from the finite lifetime of the |f〉〈g| coherence induced by the classical laser pulses. While both classical and quantum light give the resonance frequency, the temporal resolution that can track the f-g coherence decay is significantly enhanced by using a highly entangled photon pair. This can be understood in a similar way to the two-photon absorption with entangled photons where the product of temporal and spectral resolutions violates the uncertainty relation.

Fig. 5: 2D photon coincidence counting signal.
figure 5

Pab(Δ,ωp) [Eq. (7)] for the model system of Fig. 2b. The pump frequency ωp creating the entangled photon pair and the optical delay between two arms are varied. We approximate a sinc-shape of the two-photon wavefunction by a Gaussian for simplified frequency integration: \(\begin{array}{l}{\Phi} (\omega _1,\omega _2) = (2\pi \sigma _ + \sigma _ - )^{ - 1/2}{\mathrm{exp}}\left[ { - \left( {\omega _1 + \omega _2 - \omega _{\mathrm{p}}} \right)^2/(16\sigma _ + ^2)} \right] {\mathrm{exp}}\left[ { - \left( {\omega _1 - \omega _2} \right)^2/(4\sigma _ - ^2)} \right]\end{array}\). a Two-photon wavefunction of unentangled photons with σ+ = 0.1 eV, σ− = 0.2 eV. b The Hong-Ou-Mandel (HOM) spectrum using the two-photon state in (a). c Two-photon wavefunction of highly entangled twin photons with energy anti-correlation. Here σ+ = 0.1 eV, σ− = 0.8 eV. d The HOM spectrum obtained using the twin-photon state in (c). The resolution is clearly enhanced by the entangled photon pair.

Full size image

The quantum light statistics is modified by interaction with matter. To understand the nature of the change and the matter information it carries, we have used the HOM interferometric setup which provides information about the state of light after the interaction with matter. Ultrashort pulses can exploit the quantum nature of light in order to increase the measurement accuracy of a classical response function. This was studied in detail for a model system.

Interaction of quantum systems changes their state in the course of light-matter interaction at a single-photon regime20,21,22. Each interaction enhances the correlation, and the system becomes more inseparable. This may be employed in novel quantum spectroscopic setups, which extract matter information from optical probes. While single-photon states can be easily described in the photon number (Fock) basis, they are less suitable for probing phase-shifts due to number-phase uncertainty23,24. Multiphoton (entangled) states provide a richer playground for improving the temporal resolution imprinted by matter on the optical probe and is the focus of our study. Multimode squeezed states25 may be useful since the number-phase uncertainty can be further tuned in order to reach a desired joint frequency-time resolution.

Methods

Optical signals description

We start with the joint light-matter Hamiltonian,

$$\hat H = \hat H_\mu + \hat H_\phi + \hat H_{\mu \phi },$$
(9)

where μ, ϕ represent the matter and electromagnetic field, respectively, and \(\hat H_{\mu \phi }\) is their coupling. The electric field operator is partitioned into positive and negative frequency components,

$$\begin{array}{*{20}{c}} {{\hat{\mathbf{E}}}\left( {{\mathbf{r}},t} \right) = \mathop {\sum}\nolimits_{s = 1}^{n + 1} {{\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},t} \right) + {\hat{\mathbf{E}}}_s^{\left( - \right)}\left( {{\mathbf{r}},t} \right),} } \\ {{\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},t} \right) = \left[ {{\hat{\mathbf{E}}}_s^{\left( - \right)}\left( {{\mathbf{r}},t} \right)} \right]^\dagger ,} \end{array}$$
(10)

where the sum over s runs over the modes participating in the wave-mixing experiment, the positive frequency component (h.c. of the negative counterpart) in the continuum limit is expressed in the slowly varying amplitude approximation,

$${\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},t} \right) = \left( {\frac{{\hbar \omega _s}}{{2\pi }}} \right)^{\frac{1}{2}}e^{i{\boldsymbol{k}}_{\boldsymbol{s}}{\boldsymbol{r}}}{\int} {d\omega \hat a_s(\omega )e^{ - i\omega t}}$$
(11)

with the canonical bosonic commutation relations \(\left[ {a_s\left( t \right),a_{s\prime }^\dagger \left( {t^\prime } \right)} \right] = \delta _{ss\prime }\delta \left( {t - t^\prime } \right)\). Given the dipole operator \(\hat \mu = \hat V + \hat V^\dagger\), the light-matter interaction in the rotating wave approximation (RWA) is given by,

$$\hat H_{\mu \phi } = {\hat{\mathbf{E}}}^{\left( - \right)}\left( {{\mathbf{r}},t} \right)\hat V\left( {{\mathbf{r}},t} \right) + {\hat{\mathbf{E}}}^{\left( + \right)}\left( {{\mathbf{r}},t} \right)\hat V^\dagger \left( {{\mathbf{r}},t} \right),$$
(12)

which associates absorption of a photon with dipole excitation and emission with deexcitation. We shall solve the equation of motion of the field in the interaction picture,

$$\frac{d}{{dt}}{\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},{\mathbf{t}}} \right) = - \frac{i}{\hbar }\left[ {{\hat{\mathbf{E}}}_s^{\left( + \right)}\left( {{\mathbf{r}},{\mathbf{t}}} \right),\hat H_{\mu \phi }\left( {{\mathbf{r}},{\mathbf{t}}} \right)} \right].$$
(13)

The entangled two-photon wavefunction

We next present the general form of the entangled two-photon wavefunction. Equations (15), (16), and (S10) are then used for two limiting cases of narrowband and broadband generating pulses. The wavefunction of frequency-entangled photons, generated by a parametric downconversion (PDC) is given by26,27,

$$|\left. \psi \right\rangle = {\int} {d\omega _ad\omega _b{\Phi} \left( {\omega _a,\omega _b} \right)a^\dagger \left( {\omega _a} \right)b^\dagger \left( {\omega _b} \right)|\left. {0_a,0_b} \right\rangle ,}$$
(14)

where Φ(ωa, ωb) is the two-photon amplitude and a†(ω) and b†(ω) are creation operators for the two modes. Here ωa/c and ωb/c correspond to the projections of the wavevectors along the crystal length, where c is a speed of light. These operators obey boson commutation relations \(\left[ {a\left( \omega \right),a\left( {\omega ^\prime } \right)} \right] = \left[ {b\left( \omega \right),b\left( {\omega ^\prime } \right)} \right] = \left[ {a\left( \omega \right),b^\dagger \left( {\omega ^\prime } \right)} \right] = 0\) and \(\left[ {a\left( \omega \right),a^\dagger \left( {\omega ^\prime } \right)} \right] = \left[ {b\left( \omega \right),b^\dagger \left( {\omega ^\prime } \right)} \right] = \delta \left( {\omega - \omega ^\prime } \right)\). For a type II phase-matched PDC process generated by a broadband pulse, the amplitude is given by pump envelope multiplied by the phase-matching factor

$${\Phi} \left( {\omega _a,\omega _b} \right) = \alpha \left( {\omega _a,\omega _b} \right)\varphi \left( {\omega _a,\omega _b} \right).$$
(15)

The Gaussian envelope is given by \(\alpha (\omega _a,\omega _b) = (2\pi \sigma _p^2)^{ - 1/2}{\mathrm{exp}}[ { - ( {\omega _a + \omega _b - \omega _p} )^2/(2\sigma _p^2)} ]\), which is inherited from the pump pulse centered around ωp with σp bandwidth. The phase-matching condition is included in the two-photon state amplitude26 \(\varphi \left( {\omega _a,\omega _b} \right) = {\mathrm{sinc}}\left\{ {L_c\left[ {\left( {\omega _a - \frac{{\omega _p}}{2}} \right)\left( {k_a^\prime - k_p^\prime } \right) + \left( {\omega _b - \frac{{\omega _p}}{2}} \right)\left( {k_b^\prime - k_p^\prime } \right)} \right]} \right\}\). Here Lc is the length of the generating nonlinear crystal, k′a,b are the inverse group velocity at half pump frequency \(\frac{{\omega _p}}{2}\) and k′p is the corresponding velocity at the central frequency ωp.

There are two limiting cases for this wavefunction. One is mostly used for ultrafast pulses resulting in wide bandwidth pump. In this case, a Schmidt decomposition to pulse-modes is useful. The other is narrowband limit in which the width of the pump envelope \(\sigma _p^2\) is set to zero. For a narrowband pump pulse, a(ωa, ωb) → δ(ωa + ωb−ωp), and the conjugate temporal profile \(\delta T = \sigma _p^{ - 1}\) is therefore large. The two-photon wavefunction then takes the form,

$$|\left. \psi \right\rangle _{nb} = {\int} {d\omega \,{\mathrm{sinc}}\left[ {\left( {{\it{\upomega }} - \frac{{{\it{\upomega }}_p}}{2}} \right)T_a + \left( {\frac{{{\it{\upomega }}_p}}{2} - {\it{\upomega }}} \right)T_b} \right]} |\left. \omega \right\rangle _a| {\omega _p - \omega } \rangle _b$$
(16)

where we have defined the time variables \(T_{a/b} = \left( {k_{a/b}^\prime - k_p^\prime } \right)L_c\). By shifting the frequency variables, we obtain

$$\left| {\left. \psi \right\rangle _{nb} = {\int} {d\omega \,{\mathrm{sinc}}\left[ {{\it{\upomega }}T_{{\mathrm{ent}}}} \right]} } \right|\left. {\omega + \frac{{\omega _p}}{2}} \right\rangle _a|\left. {\frac{{\omega _p}}{2} - \omega } \right\rangle _b$$
(17)

where Tent = Ta − Tb is the entanglement time. Note, that the wavefunction in Eq. (15) does not generally possess exchange symmetry, since the twin state represents the state of the field modes (amplitudes), which can be distinguished by, e.g., group velocity dispersion, polarization etc. In the same time, Eq. (16) yields a simplified expression originating from the narrowband pump pulse, where overlapping modes result in the exchange symmetry of the wavefunction typical for the HOM experiment. A more general treatment of the photon wavefunctions is discussed in ref. 28.