Introduction

The current-phase relationship (CΦR), describes the relation between the supercurrent, Is, through a Josephson junction (JJ) and the gauge invariant phase difference across the junction, Δθ. The exact relation is determined by the details of the Andreev bound state (ABS) spectrum that exists in the junction1,2,3. For a conventional superconductor-insulator-superconductor (SIS) junction, the current-phase relation is sinusoidal, Is = Ic sin (Δθ), where Ic is the junction critical current. With the advances in materials sciences and the realization of novel link materials, exhibiting non-conventional CΦRs, JJ with new functionalities arise having a tremendous potential for applications4,5,6,7,8,9.

To investigate the harmonic content of the current-phase relationship in these novel weak link materials, experiments relying on detecting the phase-locked response of a current driven Josephson junction when subjected to a high frequency radiation field of frequency, νrf, have recently been used10,11,12,13,14,15. In case the weak link is characterized by a conventional sinusoidal current-phase relationship, this resonant response manifests itself as constant voltage plateaus, so called Shapiro steps, in the voltage versus current (VI)-characteristics of the junction at voltages Vn = nΦ0νrf, where \(n \in {\Bbb Z}\) and Φ0 the fluxquantum16. However, for a weak link having a 2π periodic non-sinusoidal CΦR, the response exhibits, in addition to the conventional integer Shapiro steps, steps at fractional values Vn/q = (n/q)Φ0νrf, where the qth (q ≠ n) fractional step originates from the phase-locked response with the qth harmonic of the CΦR17,18,19. Similarly, the 4π periodicity of the Majorana bound state spectrum in topological Josephson junctions, is expected to leave a fingerprint in the Shapiro step response10.

Despite the experimental accessibility of these techniques, the detailed interpretation of such experiments is complicated by the non-linear nature of the Josephson response10,15,20,21. Moreover, the use of a single junction makes these experiments challenging mainly due to its low response (or radiation power) and small impedance12,22. Josephson junction arrays (JJAs) containing many junctions provide the natural alternative to provide the necessary enhancement of the coherent response and the design degree of freedom allows to tune their impedance for optimum integration in the measurement/excitation circuit23,24,25. Although JJAs hold a strong promise to study the CΦR, the array geometry has been predominantly studied as a model system for the Kosterlitz-Thouless (KT) transition and the fully frustrated XY-model26,27,28,29,30,31. Whereas, the impact of the particular CΦR on their high frequency response remains until now unexplored.

In this paper, we first explore the dependence of the giant Shapiro response on the anisotropy of the array. We demonstrate that for highly anisotropic arrays, the giant collective high frequency response reflects the properties of a single junction. Further, we demonstrate experimentally the appearance of giant fractional Shapiro steps in anisotropic Josephson junction arrays as unambiguous evidence of a non-sinusoidal CΦR.

Results

We present transport measurements on 2D proximity-induced superconductor-normal metal-superconductor (SNS) Josephson junction arrays having very different lattice parameters (Fig. 1a). The JJAs consist of a rectangular lattice of square 25 nm-thick molybdenum germanium (Mo79Ge21) superconducting islands, on top of a metallic gold (Au) film that couples the superconducting islands through the proximity effect32. We define the anisotropy, η = dy/dx, of the rectangular array as the ratio of the spacing between islands perpendicular, dy, and along the current direction, dx. For both devices the spacing along the current direction is quasi identical, dx = 250 nm, while the spacing perpendicular to the current direction, dy, varies. Device 1 has an anisotropy of η = 0.8. Whereas, Device 2 has a large anisotropy of η = 4. Further, Device 1 has Nx = 200 columns of Ny = 13 square islands, while for Device 2, Nx × Ny = 160 × 6. We define the x-direction to be colinear with the current bias and the magnetic field is always applied along the z-direction. Due to the similarities between the physics of JJAs and the XY-model, we express the applied magnetic field in reduced units, f  = H/H1, known in the JJA literature as frustration. Where H1 = Φ0/A, with A the area of the unit cell of the JJA. For Device 1, H1 = 3.7 mT, while for Device 2 having the larger unit cell, H1 = 1.8 mT.

Fig. 1: Sample layout and DC transport measurements.
figure 1

a A schematic illustration, together with a false-coloured scanning electron microscopy image (of Device 1), of the superconductor-normal metal (S–N) hybrid devices studied in this work. The black scale bar corresponds with 200 nm. b The temperature, T, and DC current, IT, dependence of the Device 2 differential resistance, dVT/dIT, under a zero applied magnetic field condition. NS, VS and Z–VS indicate the normal state, voltage state and zero-voltage state of the Josephson junction array, respectively. Concerning the discontinuity of the VS-NS transitions around T = 1.8 K we refer to the Methods section-electrical characterization. c A few representative voltage, V, versus current, I, curves and d dV/dI − I curves at different temperatures for a single junction in Device 2. e The temperature dependence of the critical current, Ic, of a single junction for both Devices (red open circles for Device 2, blue open circles for Device 1) as extracted from Fig. 1b (and similar data for Device 1). The solid lines show the fit using the high temperature limit of Likharev’s theory for long diffusive SNS-junctions.

Full size image

Both devices show global superconductivity having a critical temperature of Tc = 4.0 K and Tc = 4.15 K, for Device 1 and 2, respectively33,34. To obtain the characteristics of an individual junction out of measurements reflecting the collective response of the whole array, we measured the VI-characteristics in a highly symmetric situation (zero frustration) where each junction probes the same current. This condition is achieved under zero-field, where the applied current, IT, is distributed equally between the rows, in a way that each junction parallel to the current is crossed by a current I = IT/Ny35. In such state, the junctions perpendicular to the current are never activated, while the voltage across each parallel junction is V = VT/(Nx − 1), with VT the corresponding total value measured along the array. The temperature dependence of the differential resistance, dVT/dIT(T), of the arrays under zero external magnetic field while sweeping the bias current for temperatures ranging from 0.3 to 5 K is shown in Fig. 1b (for Device 2).

It is clear from Fig. 1b that for currents below the critical current, Ic(T), the JJA is in the zero-voltage state, where the current is a pure supercurrent. When the current bias exceeds the critical current, the extra current is carried by a resistive channel of quasiparticle excitations and the JJA resides in the voltage state, which exhibits a linear current-voltage relation (see Fig. 1c, d). Finally, when the current bias reaches the de-pairing current, the sample will transit to the normal state. A clear fingerprint of the nature of the weak link is given by the temperature dependence of Ic(T). As shown in Fig. 1e, Ic(T) exhibits an exponential decay with T at high temperatures and saturates at lower temperatures, consistent with Likharev’s conventional theory of long diffusive SNS junctions (see Supplementary Information Note 1.1)34. In this case, the CΦR can be written as:

$$I_{\mathrm{s}} = I_{\mathrm{c}}\sin \left( {\Delta \theta - \ell (T)\frac{{I_{\mathrm{s}}}}{{I_{\mathrm{c}}}}} \right)$$
(1)

where Ic = max(|Is|) is the junction’s critical current and the temperature dependent parameter, \(\ell \left( T \right) = I_{\mathrm{c}}\left( {\frac{{dI_{\mathrm{s}}}}{{d\Delta \theta }}} \right)_\pi ^{ - 1} + \,1\), has a simple geometrical interpretation, as it determines the level of skewness of the CΦR2,35 Whereas, at high temperatures the current-phase relationship is harmonic \(\ell = 0\), at low temperatures the current-phase relationship becomes considerably forward-skewed \(0 \, < \, \ell \, < \, 1\). As a result, the array of long diffusive SNS-junctions (dx/ξN(Tc) ~ 5, with ξN the normal metal coherence length, (see Supplementary Information Note 1.1)) provides a prototypical system to investigate the effect of the harmonic content in the CΦR on the high frequency response, as it can be easily tuned by temperature3,36.

Giant Shapiro response at integer frustration

We initially investigate the high frequency response at high temperatures, where the current-phase relation of an SNS junction is sinusoidal, \(\ell = 0\). Due to the smallness of the fluxquantum, \({\mathrm{\Phi }}_0^{ - 1} = 483.6\,{\mathrm{MHz}}/\mu {\mathrm{V}}\), typically microwave excitation frequencies (νrf > 1 GHz) are necessary in order to observe measurable Shapiro steps, Vn. By constructing a (Nx − 1) × (Ny − 1) Josephson junction network the Shapiro step response is multiplied by a factor Nx − 1, resulting in a giant Shapiro response at \(V_{\mathrm{n}}^{\mathrm{T}} = (N_{\mathrm{x}} - 1)V_{\mathrm{n}}\) and becomes, for the array size of the devices considered in this work, measurable at radio frequencies (RF) as low as 50 MHz. The scaling in the transverse direction, Ny, increases the overall critical current of the device.

A typical Shapiro response for Device 1 is shown in Fig. 2a at f = −1, which similarly to f = 0 results in a highly symmetric (non-frustrated) situation where the whole JJA behaves as a single JJ. Both the time averaged VI-scan at T = 3 K and the differential resistance VT/dIT, are shown using a current bias, IT = Idc + Irf(t).  Where, Idc is a DC current and Irf(t) = Irfcos(2πνrft) is an RF excitation of amplitude Irf and frequency, νrf = 200 MHz. Note, that since the RF excitation is experimentally applied by a function generator, the conversion between the applied AC voltage, Vrf, and the transmitted AC current, Irf, is a priori unknown (see Supplementary Information Note 2). The pronounced Shapiro response at the voltage values \(V_n^{\mathrm{T}} = n(N_{\mathrm{x}} - 1){\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}}\), with Nx = 200, indicates that the whole Josephson junction network has a coherent response under RF excitation, in which all Nx − 1 = 199 junctions contribute, despite the presence of an unavoidable disorder in the system due to sample fabrication37. Figure 2b, shows the experimentally measured frequency dependence for a fixed RF excitation amplitude for Device 1. Shapiro steps are clearly reflected in the map, as the zones of low differential resistance (yellow). The black stripe lines indicate the expected theoretical nth Shapiro step response. The linear evolution of integer Shapiro steps down to 50 MHz, directly show the gained resolution of the JJA compared to a single junction and its potential to explore the properties of a single junction using the collective response of the JJA12.

Fig. 2: Giant Shapiro step response and frequency dependence of the Shapiro steps.
figure 2

a A typical Shapiro response curve of Device 1, where both the time averaged voltage, VT, versus current, IT, at T = 3 K and the differential resistance, dVT/dIT, simultaneously measured by a standard lock-in technique are shown. The radio frequency (RF) excitation parameters are Vrf = 100 mV and νrf = 200 MHz. The x-axis is scaled by \(V_1^{\mathrm{T}} = (N_{\mathrm{x}} - 1){\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}} = 82.3\,\mu {\mathrm{V}}\), where Φ0 is the fluxquantum, νrf the RF frequency of the drive and Nx = 200. b The experimentally measured frequency dependence of the Shapiro steps for a fixed RF excitation amplitude of Vrf = 100 mV for Device 1. Shapiro steps are clearly reflected in the map, as the zones of low differential resistance (yellow). The black stripe lines indicate the expected theoretical nth Shapiro step response according to \(V_n^{\mathrm{T}} = n(N_{\mathrm{x}} - 1)\Phi _0\nu _{{\mathrm{rf}}}\).

Full size image

Recent works, exploring topological weak links, have shown that a Shapiro map is a powerful representation of the response at a fixed RF frequency to obtain information regarding the weak link CΦR10,11,38. A Shapiro map traces the widths of the observed plateaus as a function of the AC drive amplitude and DC current bias. For a current biased system, the width of the Shapiro current plateaus can deviate from the ideal Bessel dependence, expected for a JJ which is voltage biased. For the current biased case the current width of the nth Shapiro step depends in a non-trivial way on the reduced frequency21,37,38,39,40:

$${\mathrm{\Omega }} = \frac{{{\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}}}}{2{\pi}{RI_{\mathrm{c}}}}$$
(2)

where R is the resistance of the Junction. For an harmonic CΦR, it has been shown in refs. 20,21 that the current step widths of the integer Shapiro steps follow qualitatively a Bessel like dependence ΔIn ~ IcJn(Irf/Ω), with Jn the nth order Bessel function of the first kind. Only in the case of low AC current amplitudes, low reduced frequencies and low Shapiro step numbers, the step widths will deviate qualitatively from the Bessel like dependence.

Figure 3a shows the experimentally measured Shapiro map, as a function of the AC drive amplitude and DC current for a fixed radio frequency, νrf = 150 MHz (corresponding to Ω ~ 0.12), for Device 1. At the lowest RF powers, the influence of the irradiation is small and only the n = 0 plateau, corresponding with the zero-voltage state is observed. Upon increasing the RF power, the map starts to show higher order Shapiro plateaus. Only integer Shapiro steps are present in the map. It is clear that depending on the RF amplitude a different Shapiro step response will be observed. For example, while for Vrf = 240 mV, we will encounter dominantly odd Shapiro steps. For Vrf = 300 mV we will encounter dominantly even Shapiro steps in the VI-characteristic. Similar observations can be made when varying the RF frequency or temperature (See Fig. 1b and Supplementary Information Note 3). This even-odd effect41, results in the conspicuous absence of steps at particular RF amplitudes or frequencies and is attributed to the oscillatory dependence of the width of the Shapiro current plateaus on the reduced frequency21. Figure 3b shows the Shapiro response obtained within the RSJ model (see Methods section) for a single junction having a sinusoidal CΦR. The simulated response shows excellent quantitative agreement with experiment, apart from a small error (clearly observed at Idc = 0 μA) in the oscillation period of the Shapiro step widths with the AC drive amplitude. This error results from a small mismatch between the Irf current value used in the extended RSJ model and the Vrf value, which is experimentally applied. This indicates that our JJA can be well described by the current driven RSJ model for a single junction.

Fig. 3: Current biased Shapiro map.
figure 3

a, b show the evolution of the Shapiro steps as a function of radio frequency (RF) amplitude in a so called Shapiro map. In particular the experimentally obtained dependence of the differential resistance, dVT/dIT, as a function of the AC drive amplitude, Vrf, and DC current, \(I_{{\mathrm{dc}}}^{\mathrm{T}}\), for a fixed radio frequency, νrf = 150 MHz, for Device 1 at T = 3.3 K is shown in a. The Shapiro map generated from the extended resistively shunted Josephson junction (RSJ) model (see Methods section) for a single junction is shown in b. In the latter case, the differential resistance is multiplied by a factor 199/13, the current by a factor 13 and the voltage with a factor 199, in order to obtain the corresponding cumulative array response. c The width of the first four Shapiro steps, ΔIn for n = 0, 1, 2, 3, are plotted in function of the RF amplitude, \(I_{{\mathrm{rf}}}^{\mathrm{T}}\). The lines show a fit using a Bessel dependence with parameters, A = 30.12 μA and β = 0.0767 μA−1.

Full size image

Figure 3c shows the evolution of the first n = 0, 1, 2, 3 Shapiro current step widths with applied RF amplitude, extracted from the experimental data (dots) in Fig. 3a. Although, the behavior of the step widths for the current biased case are known to deviate from the ideal Bessel dependence, for the high value of the reduced frequency, Ω = 0.12, a qualitatively similar behavior is found as indicated by the fit (solid lines)21,39.

Giant Shapiro response at non-zero frustrations

The applied magnetic field provides an interesting experimental knob to modify the response of the system as it has a direct impact on the critical current and, as a result, on the reduced frequency. In addition, a magnetic field induces frustration in the JJA and a detailed investigation is required to differentiate both effects. Figure 4a shows the measured and simulated contour map of the differential resistance as a function of frustration and reduced DC voltage, \(V_{\mathrm{T}}/V_1^{\mathrm{T}}\), for T = 3 K. For f ∈ [−2, 2] strong Shapiro features can be observed at integer values of the frustration, whereas shallow features can also be observed near half-integer values of the frustration (see Supplementary Information Note 4 and 5). The observation of giant Shapiro steps at fractional or integer multiples of the frustration is due to coherent dynamics of the vortex lattice under RF excitation when commensurability exists between the magnetic field induced vortex lattice and the underlying Josephson junction lattice26,27,28,29,30. Deviating from these high symmetry conditions (i.e. inducing frustration), results in a suppression of the coherent response of the JJA. The high symmetry conditions at particular filling factors are independently confirmed trough increased critical current values at the same magnetic field values for T = 2 K (Fig. 4b).

Fig. 4: Field dependence of the Shapiro response and field dependence of the critical current.
figure 4

a Field dependence of the Shapiro response for Device 1, presented as a contour map of the differential resistance, dVT/dIT, versus frustration, f, and the DC voltage, VT, at T = 3 K. The DC voltage is scaled by \(V_1^{\mathrm{T}} = (N_{\mathrm{x}} - 1){\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}} = 61.7\,\mu {\mathrm{V}}\), where Φ0 is the fluxquantum and νrf the radio frequency (RF) of the drive. The experimental measurement using an RF excitation of νrf = 150 MHz and Vrf = 100 mV, is shown for negative frustrations. The result obtained within the extended resistively shunted Josephson junction (RSJ)-model for a 13 × 13 array, using an RF excitation, Irf = 7.69 μA applied to each junction is shown for positive frustrations. The differential resistance obtained from the simulation for a 13 × 13 array is multiplied by a factor 13(Nx − 1)/(12Ny), in order to match the value for the array size, (Nx − 1) × Ny of the experiment, with (Nx, Ny) = (200, 13). b Frustration dependence of the voltage, VT, versus current, IT, characteristics of Device 1 at T = 2 K when no RF excitation is applied, the black contour line indicates the evolution of the critical current as determined by using a voltage criterion of 0.1 μV. c Field dependence of the Shapiro response for Device 2. The experimentally measured contour map of the differential resistance versus frustration, f and the DC voltage, VT, for T = 1.8 K is shown for negative frustrations. The RF excitation parameters are νrf = 175 MHz and Vrf = 800 mV. The DC voltage is scaled by \(V_1^{\mathrm{T}} = (N_{\mathrm{x}} - 1){\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}} = 57.5\,\mu {\mathrm{V}}\). The result obtained within the extended RSJ-model for a single junction, for an RF current bias of Irf = 200 μA applied to the junction, is shown for positive frustrations. The differential resistance obtained from the simulation for a single junction is multiplied by a factor (Nx − 1)/Ny, in order to match the value for the array size, (Nx − 1) × Ny of the experiment, with (Nx, Ny) = (160, 6). At low fields f = [−6, 0] the experimental data shows qualitatively similar modulations with the magnetic field, f, which cannot be resolved with the current colour scale. d Field dependence of the differential resistance of Device 2 at T = 2 K when no RF excitation is applied, the black contour line indicates the evolution of the critical current using a resistance criterion of 5 Ohm.

Full size image

The high anisotropy of the array in Device 2 (and consequently the critical current, see Supplementary Information Note 1.4), is expected to result in a strong suppression of effects related to flux quantization in the array. Consequently, the anisotropic JJA is expected to reflect single JJ behaviour, while simultaneously keeping the advantages of high device critical currents and giant Shapiro responses, the array geometry provides. However, disorder in the array, inherent to the fabrication process, might induce broadening of the Shapiro steps42. Figure 4c shows the measured and simulated contour map of the differential resistance as a function of the applied magnetic field and reduced DC voltage, \(V_{\mathrm{T}}/V_1^{\mathrm{T}}\), for Device 2 at T = 1.8 K. The observed magnetic field dependence can be explained by the variation of the critical current with field at T = 2 K, shown in Fig. 4d, exhibiting the typical Fraunhofer-like dependence, illustrative for a single uniform weak link. We can estimate the junction area by fitting the Ic(B, T) with the Fraunhofer function (see Supplementary Information Note 1.3). This provides us with an estimate of the effective area of the parallel junctions to be 0.173 μm2, which corresponds well with the geometric area of the parallel junction, 0.125 μm2. This single junction behaviour of the highly anisotropic JJA, Device 2, is further evidenced by performing simulations within the extended RSJ model on a single junction, showing excellent agreement with experimental observations (see Supplementary Information Note 6).

Giant fractional Shapiro response

The enhanced Shapiro response in anisotropic JJAs, free from spurious effects due to flux quantization, provides an excellent playground to investigate the CΦR by probing their RF response and potentially their enhanced RF emission spectra12. As discussed, at low temperatures the CΦR of the SNS junctions is expected to become considerably skewed. In this case it is expected that fractional Shapiro steps can appear due to phase locking between the incident RF radiation and a higher harmonic of the CΦR17,18,19.

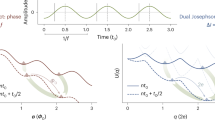
Figure 5a (negative field values), shows the experimentally obtained field dependence of the Shapiro response for the anisotropic JJA (Device 2) at T = 0.4 K. Some clear differences can be observed with the map at T = 1.8 K (Fig. 4c). The most pronounced difference is the observation of giant half-integer Shapiro steps at larger values of the frustration (see Fig. 5b). As the anisotropic array exhibits single junction behaviour, the half-integer steps have to originate from an intrinsic property of the single junctions within the array. To this end, we show in Fig. 5a (positive field values) the simulated field dependence for a 6 × 6 array using the anisotropic array junction parameters (for simulations on a single junction, see Supplementary Information Note 7), including the possibility of a single-valued, but skewed CΦR, \(0 \, < \, \ell \, < \, 1\). We used \(\ell = 0.5\), which corresponds to the low temperature limit obtained from the semi-classical theory for a junction of length L = 4.4ξN(Tc)34. Both simulation, on an array and a single junction, reproduce the appearance of half-integer Shapiro steps at higher field values observed experimentally and confirm that the half-integer Shapiro resonances can be unambiguously attributed to a prominently skewed CΦR.

Fig. 5: Giant fractional Shapiro steps.
figure 5

a Field dependence of the experimentally obtained Shapiro response for Device 2. For negative frustrations the experimentally measured contour map of the differential resistance, dVT/dIT, as a function of reduced field, f, and reduced DC voltage, VT, for T = 0.4 K is shown. The radio frequency (RF) excitation parameters are νrf = 200 MHz and Vrf = 1000 mV. The DC voltage is scaled by \(V_1^{\mathrm{T}} = (N_{\mathrm{x}} - 1){\mathrm{\Phi }}_0\nu _{{\mathrm{rf}}} = 65.8\,\mu {\mathrm{V}}\), where Φ0 is the fluxquantum and νrf the radio frequency of the drive. The result obtained using the extended resistively shunted Josephson junction (RSJ)-model (see Methods section) for a 6 × 6 array, including the field dependence of the critical current, a skewed current-phase relationship (CΦR) with \(\ell = 0.5\) (see Methods section) and using an RF excitation, Irf = 300 μA applied to each junction, is shown for positive frustrations. The value for the differential resistance is multiplied by a factor 6(Nx − 1)/(5Ny), in order to match the value for the array size, (Nx − 1) × Ny of the experiment, with (Nx, Ny) = (160, 6). b The average differential resistance, \(\left\langle\frac{{dV_{\mathrm{T}}}}{{dI_{\mathrm{T}}}}\right\rangle_{7 < f < 9}\), in the range 7 < f < 9 versus the reduced DC voltage, indicating clearly the presence of fractional Shapiro steps.

Full size image

Further, Fig. 5a shows the evolution of dominantly even steps at low frustrations, |f| < 2, to dominantly odd steps at frustrations 2 < |f| < 4, and eventually to a combination of half-integer and integer steps at |f| > 4. The simulated maps feature a similar field dependence. This intriguing field dependence can be directly related to the evolution of the Shapiro step widths with the reduced frequency, Ω. For Device 2, the reduced frequency changes considerably from Ω = 0.0063 to Ω = 0.0307 when increasing the magnetic field from f = 0 to f = 10 due to the Fraunhofer-like field-dependence of the critical current.

Figure 6a shows synchronization diagrams in the Irf/Ic − Idc/Ic parameter space for reduced frequencies Ω = 0.0063, corresponding to Device 2 under 200 MHz excitation and frustration f = 0 (Ic(f = 0) = 49.7 μA), and Ω = 0.0307 corresponding to Device2 under 200 MHz and frustration f = 10 (Ic(f = 10) = 10.22 μA). For = 0.0063, integer Shapiro steps essentially fill the whole Shapiro step diagram, leaving no room for fractional steps to show up. For a higher reduced frequency, Ω = 0.0307, the integer Shapiro steps become narrower leaving room to the concomitant emergence of half-integer resonances. The horizontal line indicates the estimated RF current amplitude used in the measured field dependence (Fig. 5a) and indeed confirms that at f = 0 (Ω = 0.0063) no fractional Shapiro steps can be observed, while at f = 10 (Ω = 0.0307) half-integer steps show a pronounced fingerprint. Further, a myriad of fractional resonances, corresponding to phase locking to different harmonics of the CΦR, can be found, as shown in the inset. These, however, are considerably narrower than the half-integer ones and thereby more susceptible to being washed out by thermal fluctuations. The complete evolution of the Shapiro step widths with reduced frequency is shown in Fig. 6b as obtained for a reduced RF amplitude of Irf/Ic = 6.04, corresponding to the f = 0 case. It is clear that for this reduced RF amplitude fractional steps become appreciable only above Ω = 0.01 (see Supplementary Note 8).

Fig. 6: Theoretical Shapiro step diagrams.
figure 6

a, b Theoretical Shapiro step diagrams for a skewed current-phase relationship (CΦR) with \(\ell = 0.5\) and reduced frequencies Ω = 0.0063 (a) and Ω = 0.0307 (b), featuring integer (orange fills delimited by black lines) and fractional (red, purple, crimson, and maroon fills, as indicated in the inset) Shapiro steps. Inset: zoomed-in region of the Ω = 0.0307 diagram showing n/q resonances for q = 2, 3, 4, and 5. c Width of selected Shapiro steps (n = 0, 1, 1/3, 1/2) as a function of reduced frequency for fixed reduced radio frequency (RF) amplitude Irf/Ic = 6.04. d The width of the fractional steps are reproduced in an enlarged vertical scale.

Full size image

Discussion

In this work, we demonstrated that for a prototypical SNS-based JJA, the presence of fractional steps at the lowest explored temperature of T = 0.4 K, demonstrates unambiguously that the CΦR is considerably skewed, with \(\ell = 0.5\). This value corresponds well with the value expected within the equilibrium quasi classical theory3,35. Note however, that non-equilibrium effects, inherent to the measurement technique, can modify the occupation of the ABS that persist up to high temperatures14,36,43,44,45,46,47. The giant Shapiro response in a JJA, in contrast to a single junction, enables to measure the RF response using sub gigahertz frequencies. It allows, similarly as in Dassonneville et al.46, to explore the impact of these non-equilibrium processes on the ABS over a wide range of frequencies. Further, we have shown that a complete picture of the response is necessary in order to obtain information about the CΦR from the complex non-linear response.

Methods

Device fabrication

The devices shown in Fig. 1a consist of a rectangular lattice of square superconducting islands, which are deposited on top of a metallic gold (Au) film, patterned for four-point transport measurements using standard e-beam lithography. The superconducting square islands are 25 nm-thick molybdenum germanium (Mo79Ge21) thin films of size a = 500 nm deposited using pulsed layer deposition. To prevent oxidation they are in-situ covered by a 5 nm-thick Au capping layer. The Au film underneath the array is deposited on a Si/SiO2 substrate using molecular beam epitaxy. A 5 nm-thick titanium sticking layer is used to assure good adhesion of the Au film onto the substrate. Device 1 has a 40 nm-thick Au base layer. Whereas, Device 2 has a 30 nm-thick Au base layer.

Electrical characterization

The devices are wired to a chip carrier that can be placed in two variable temperature cryostats. Measurements for temperatures in the range 0.3–1.6 K are performed in a He3 system, while the high temperature range is explored in a He4 flow cryostat. Due to the reduced cooling power of the He3 system, the SN-transition in Fig. 1b shifts towards lower currents. For the four-terminal transport measurements, characterizing the sample (Fig. 1b), we measure the differential resistance using a standard lock-in technique.

The Shapiro response presented in Figs. 4a, c and 5a are measured by simultaneously biasing the JJA with a DC current bias (Keithley 6221) and an RF AC voltage drive (Rhode&Schwarz SMY signal generator), while measuring the differential resistance using a standard lock-in technique. The corresponding voltage value is obtained by integrating numerically the differential resistance. The Shapiro responses presented in Figs. 2b and 3a are not performed with a lock-in amplifier in order to obtain directly dVT/dIT. Instead we measured VTIT-curves and calculated the derivative, dVT/dIT, using a 9-point central difference stencil method.

Extended RSJ-model

To understand our experimental findings, we model the square lattice of Nx × Ny superconducting islands on a thin metallic layer as an array comprising overdamped Josephson junctions, each shunted by a resistive load26,34,39,48,49. The junctions forming the array correspond to the SNS-junctions formed between nearest neighbouring islands as illustrated in Fig. 1a. Within this extended resistively shunted JJ model (RSJ-model), the current Iij from the ith to the jth island is given by:

$$I_{ij} = I_{{\mathrm{s}};ij}\left( {\theta _{ij} - a_{ij}} \right) + \frac{\hbar }{{2eR_{ij}}}\frac{{d\left( {\theta _{ij} - a_{ij}} \right)}}{{dt}} + \gamma _{ij}\left( t \right)$$
(3)

The first term on the right hand side in Eq. 3 describes the supercurrent, Is;ij, through the junction which is a function of the gauge invariant phase difference over the junction, θij − aij. Where, θij = θj − θi and θi is the phase on island i. Further, \(a_{ij} = \frac{{2\pi }}{{{\mathrm{\Phi }}_0}}{\int}_{r_i}^{r_j} {\boldsymbol{A}} \cdot {\mathbf{dl}}\) and A is the vector potential. The relation between the supercurrent and the gauge invariant phase difference is determined by the nature and shape of the weak link and can be described, for the majority of junctions, roughly by two constants, namely, the critical current Ic;ij and \(\ell _{ij}\)35.

$$I_{{\mathrm{s}};ij}\left( {\theta _{ij} - a_{ij}} \right) = I_{{\mathrm{c}};ij}\sin \left( {\theta _{ij} - a_{ij} - \ell _{ij}\frac{{I_{ij}}}{{I_{{\mathrm{c}};ij}}}} \right)$$
(4)

Note that \(\ell _{ij}\) has a simple geometrical interpretation and determines the skewness of the CΦR. For a sinusoidal CΦR, \(\ell _{ij} = 0\); In case the curve is forward-skewed and single valued as expected for high transmission SNS-junctions, \(0 \, < \, \ell _{ij} \, < \, 1\). The second term on the right hand side in Eq.3 is the current through a resistive shunt having resistance Rij and it stems from a dissipative quasiparticle current. Finally, the third term on the right hand side in Eq.3 is a current contribution due to thermal fluctuations, taken into account as a Langevin noise in the junction, with covariance \(\langle \gamma \left( t \right)\gamma \left( {t^{\prime}} \right)\rangle = \left( {\frac{{2k_{{B}}T}}{R}} \right)\delta (t - t^{\prime} )\).

Since in our experiment, the effective penetration depth Λ, exceeds the width of the transport bridge in the whole temperature range, Λ > Ny(a + dy), the self-field induced by the current through the junctions can be neglected and the vector potential can be approximated by \({\boldsymbol{A}} = Bx{\hat{\boldsymbol{y}}}\), where B is the magnitude of the applied magnetic field50. The equations of motion for each junction are coupled to each other by the requirement that the current coming in-and out each superconducting island is conserved, that is, for each SC island i,

$$\mathop {\sum}\limits_j {I_{ij}} = I_i$$
(5)

where j is restricted to the neighboring cells and Ii is the current injected directly into the island due to an external current bias. Meaning Ii = I for the islands at the left boundary, Ii = −I for those at the right boundary, and 0 otherwise. As the impedance of the junctions are much smaller than the impedance of the external drive and system, describing the drive as a current biased system is justified22. The system of coupled stochastic equations is integrated following a predictor-corrector scheme with time step Δt = 0.01τJ, where τJ = ħ/2eRIc is the phase particle relaxation time, which sets the typical time scale for the phase to adapt to a change of the drive current. The junctions parameters Rij and the critical current Ic;ij(B, T), can be determined from experiments (see Supplementary Information Note 1.2). The field and temperature dependence of Ic;ij is explicitly included in the simulations. More details about the numerical method can be found in the Supplementary Information Note 8.