Introduction

In recent years, van der Waals (vdW) heterostructures based on transition metal dichalcogenides (TMDs) are being studied extensively, due to their excellent electronic and opto-electronic properties1,2,3,4 with potential applications such as transistor,5 photo detector,6, 7 light-emitting diode (LED),8,9,10 and solar cells.11, 12 Atomically sharp interfaces with intralayer high carrier mobility and lack of dangling bonds result in unique spatial charge separation13 between the layers, as well as produce long-lived interlayer excitons14 under light exposure. These TMD-based vertical heterostructures have shown potentials as p–n junction and most of these p–n junctions show antiambipolar transconductance behavior.15,16,17,18,19,20,21 However, p–n junction made of single layer of TMDs, known as atomically thin p–n junctions,22,23,24,25 show quite different type of charge transport mechanism compared to the conventional p–n junction. Here, transport occurs via tunneling of carriers from one layer to the other layer.6, 25 This tunneling at the interfaces is predicted to be governed by Shockley-Read-Hall (SRH) or by Langevin recombination mechanisms.25 The band engineering of vertical heterostructures26 with available TMDs having different band gaps and work functions have paved the way to investigate the charge transport mechanisms in atomically thin p–n junction.

In this work, we have carried out electrical and photo-conductivity measurements of vertical heterostructures made of a few-layers MoTe2 (~6 layers) and single-layer MoS2. The junction current (I DS) vs. bias (V DS) data show the characteristics of a p–n junction. Interestingly, the I DS as a function of back gate voltage (V BG) show an unusual dip at the highest conductance value on top of the usual antiambipolar nature.15,16,17,18,19,20,21 We further show that the magnitude and the position of the dip in I DS–V BG curve can be modulated by changing the incident power density of light. This unique observation can be explained by including interlayer recombination rate of charge carriers along with the individual layer response. We also report very high photo-responsivity of ~105 A/W under forward bias 1.5 V at room temperature. It is seen that the photo-responsivity for blue (450 nm) and red (650 nm) light is few orders of magnitude higher than near infrared (IR) (850 nm) light. We have further carried out first principles-based density functional theory (DFT)- nonequilibrium Green’s function (NEGF) calculations, which do capture the evolution of the above mentioned dip.

Results

Experimental results without light

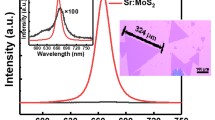
The schematic of the device and the experimental setup are shown in Fig. 1a. Oxidized silicon wafer with 285-nm thick SiO2 layer was used as a substrate for the heterojunction devices. Few-layer MoTe2 was exfoliated on the wafer, followed by transfer of a single-layer MoS2 flake using well-known polydimethylsiloxane (PDMS) dry transfer technique.27 The metal contacts on individual flakes were made using standard e-beam lithography, followed by thermal deposition of Ti/Au contacts (5/70 nm). For the electrical measurements, DC bias (V DS) was applied and the output current (I DS) was measured with a current amplifier as shown in Fig. 1a. In order to change the carrier concentration, the gate voltage (V BG) was applied to the P ++ Si substrate. The fabrication details as well as measurement details have been mentioned in the “Methods” section. Figure 1b shows the optical as well as atomic force microscope (AFM) image of one of the devices, termed as D1. As seen in Fig. 1b, the measured height of the MoTe2 flake was 4 nm, corresponding to six layers.28, 29 Figure 1d depicts the Raman spectra of the MoTe2 flake, which shows the characteristic in plane \(E_{2g}^1\) peak at 234 cm−1.24,25,26,27,28,29 The Raman spectra for MoS2 flake is shown in Fig. 1c. Here, the MoS2 characteristic \(E_{2g}^1\) and out of plane A 2g peaks can be seen, respectively, at 386 and 405 cm−1. The inset of Fig. 1c shows the MoS2 photoluminescence (PL) spectra, which shows a single peak near 625 nm. Both Raman and PL verifies that the MoS2 flake is a single layer.30, 31

Fig. 1
figure 1

a Schematics of the device, with the experimental setup. Bias (V DS) was applied to MoTe2 flake and current output was measured with a current amplifier (CA) connected to MoS2 flake. Gate voltage (V BG) was applied to P ++ Si of the substrate. LED was used to illuminate the sample for opto-electronics measurements. b Optical image (left) and AFM image (right) of the device. The scale bar (black) for optical and AFM images are, respectively, 2 μm and 1 μm. The color scale bar for AFM image is 85 nm. Inset is MoTe2 height profile along the dashed line. c Raman and PL (inset) of MoS2. d Raman for MoTe2

Full size image

Electrical and opto-electronic measurements were performed at room temperature in a vacuum of 10−5 mbar on seven devices. Though the responses were similar in all the devices, the magnitude of the response varied from sample to sample, depending on the quality of the contacts as well as the quality of the heterojunction interface. Here, we discuss four devices, for which best results were obtained. Figure 2a shows conductance (G) as a function of V BG for individual MoS2 (red curve) and MoTe2 (blue curve) for the D1 device. As can be seen in Fig. 2a, MoS2 flake is n-doped with a threshold voltage (V th) ~−20 V and MoTe2 flake is p-doped with V th ~+5 V. The I DS–V DS response of individual flakes, shown in the Supplementary Information (SI), indicates absence of any significant Schottky barriers at the contacts. Figure 2b displays the I DS–V DS response of the junction for several V BG, showing rectification behavior, expected for the p–n junction at the interface. Even though the observed I DS–V DS curve is qualitatively similar to a conventional p–n junction, the current does not increase exponentially with forward bias; rather, it increases almost linearly, pointing to the underlying rectification mechanism being different.25 The I DS–V BG plots for different V DS are shown in Fig. 2c. The overall antiambipolar shape of the curves can be understood qualitatively by considering the resistances of MoS2 and MoTe2 parts in series. At large positive V BG(V BG > 20 V) and negative V BG(V BG < −20 V) the current is very small, as one of the layer goes to the insulating state. The current is maximum near V BG ~−10 V, as expected from the conductance of individual layers seen in Fig. 2a. Though this series resistance model is able to explain the antiambipolar nature of the transconductance, it is inadequate to explain the unusual dip near the conductance maximum near −10 V. Inset of Fig. 2c shows the I DS–V BG response from yet another device (D2), which also shows similar dip near the conductance maximum (V BG ~−13 V). However, for D3 and D4 devices (Fig. 2d) no dip was observed. In the next paragraph we will show that the dip can be tailored with the incident light. The detailed characteristics of these devices are given in SI.

Fig. 2
figure 2

a Gate response of individual MoS2 (red curve) and MoTe2 (blue curve) for device D1. b I DS–V DS response of the junction. Responses for V BG −20 V to −5 V shows clear rectification behavior. c I DS–V BG response of the junction from V DS −3 V to +3 V in 0.5 V steps. An anomalous dip can be observed near the maximum of current in forward bias. Inset shows I DS–V BG response for device D2. Here also similar dip can be observed. d I DS–V BG response for device D3 and inset shows the same for device D4. No dip was observed for D3 and D4

Full size image

Experimental results with light

To further elucidate the I DS–V BG curves, we have carried out the transport measurements with the exposure of light for blue (wavelength λ ~450 nm), red (λ ~650 nm), and near IR (λ ~850 nm) LEDs on the D3 device. It was observed that the device response changed drastically with exposure of light, and even after LED was switched off the changes were retained for a long time ~24 h. First, I DS–V BG measurements are made as a function of incident light intensity (in increasing order), and then with the light off gate response is measured at regular intervals of time for several hours until the response curve is same as the initial state. Similar results were obtained in repeated runs of light-on/light-off cycles. Figure 3a shows the evolution of the gate response (at V DS = 1.5 V) under blue LED for the second cycle of measurements. It can be seen that with increasing light intensity the peak value of I DS increases and the position of the peak systematically shifts toward higher negative gate voltages. This shift of position (ΔV BG) of peak I DS as a function of power density is shown in Fig. 3d (green curve). As can be seen in Fig. 3a, the V th on the left side of the peak moves toward more negative V BG without affecting significantly the V th on the right side. This suggests that with increasing light intensity the MoS2 flake gets more n-doped, while the change in MoTe2 doping is very small. Most interestingly, the dip in gate response curve near the maximum I DS starts appearing with increasing optical power and then vanishes at higher light intensities. In the inset of Fig. 3a, we show gate response for three different light intensities during the first cycle of the measurement. The magnitude of the dip (ΔI DIP) as a function of power density is plotted in Fig. 3d (blue curve). A comparison of I DS–V DS characteristics under dark and illuminated condition at V BG = −30 V has been shown in Fig. 3b. The overall I DS–V DS curve under illumination is similar to that of the device in on-state (SI). It may be noted that the device goes from completely off-state to on-state with light. This behavior could be understood as following: at V BG = −30 V the junction does not conduct in dark state because MoS2 is completely depleted and starts conducting on light exposure, as MoS2 gets doped. Inset of Fig. 3b shows the response of the device (at V DS = 1 V, V BG = −30 V) to a very short light pulse. Though switching time from off to on state is less than ~600 mS (limited by our measuring instrument), the device shows a strong memory effect as I DS reduces slowly with time. In Fig. 3c, the evolution of gate response with time is shown after the LED was switched off (LED off part of the second cycle) and it takes almost a day for the response to come back to its initial condition. Interestingly, here also we see the dip appearing and again disappearing with time. The quantitative measure of ΔI DIP with time has been plotted in Fig. 3e.

Fig. 3
figure 3

a Evolution of I DS–V BG response of device D3, with increasing light intensity (blue) during second cycle. The dip can be seen appearing and again disappearing with increasing optical power. Inset shows evolution of I DS–V BG during first cycle. b Comparison of I DS–V DS response under dark and illuminated condition. Inset shows led pulse experiment, which shows memory effect. c Evolution of I DS–V BG with time after led was switched off. Here also the dip can be seen appearing after few hours, and then again vanishing. d, e Evolution of dip magnitude (ΔI DIP) with optical power density and time

Full size image

Photo-responsivity

Similar to the results for blue LED shown in Fig. 3, the experiments were performed with red and IR LEDs. The overall transconductance behavior of the device was similar, except for the magnitude of I DS, for all the LEDs, as shown in Fig. 4a. I ph is taken as the difference of I peak of the gate response under illumination to the corresponding I DS in gate response without illumination. As shown in Fig. 4a, I ph is maximum for the red light. In SI Fig. S5 I DS–V DS responses under dark and illuminated condition has been compared for several V BG, which shows the dependence of photo-responsivity on V DS. The highest photo response is achieved at V DS = 1.5 V, which has been plotted in Fig. 4b. The nature of plots is very similar to MoS2-graphene heterostructures.32 As can be seen, for red and blue light, photo-responsivity ~105 A/W has been achieved. For IR light (1.45 eV), the photo-responsivity is several orders of smaller (Fig. 4b) as the photon energy is below the band gap of single-layer MoS2.

Fig. 4
figure 4

For device D3. a Photo current (I ph) as function of optical power density for red (red curve), blue (blue curve), and IR (green curve) lEDs. b Photo-responsivity for red, blue, and IR light at V DS = 1.5 V. Though for red and blue the photo-responsivity was similar and of the order of 105 A/W, for IR it is several orders of magnitude small

Full size image

Discussion

Understanding the dip in photo response within a classical model

We use the interlayer recombination model25 to understand the results presented in Fig. 3. Under forward bias the charge carriers conduct via tunneling-mediated interlayer recombination as I DS ∝ R C V DS, where R C is the recombination rate. R C is proportional to n eff/τ, where n eff is effective carrier concentration and τ is interlayer tunneling time. Here, n eff = n S p T/(n S + p T), where n S and p T are the electron and hole concentrations of individual flakes, which are tuned by gate voltage as well as light intensity. In Fig. 5, the effect of photo-doping on R C has been discussed. Here, we have used the SRH mechanism for R C.25 However, similar kind of transport characteristics can be obtained from Langevin processes.25 The photo-induced doping mechanism has been illustrated schematically in Fig. 5a, where the gate voltage drops mostly across the SiO2 layer and few-layers MoTe2. The incident photons create electron-hole pairs in both MoS2 and MoTe2, but due to the presence of electric field (negative V BG) the excited electrons (holes) will move toward the MoS2 layer (MoTe2–SiO2 interface), moving the Fermi level in MoS2 closer to the conduction band (Fig. 5a). However, the photo-excited holes in MoTe2 get trapped mostly at the MoTe2–SiO2 interface as well as at the defect states inside the MoTe2 closer to its valence band, which are mostly immobile (reflected in poor mobility <1 cm2/Vs) and hence do not participate in conduction.32,33,34,35 This also explains why it takes almost a day to come back to its initial value after the light is off (Fig. 3c). The photo-induced effect has been quantitatively presented in Fig. 5b. The induced carrier concentration (n) as a function of V BG in MoS2 and MoTe2 has been generated using capacitive model, n = n 0 + C G(V BG–V th)/e, where C G is the geometrical capacitance and n 0 is the majority carrier concentration due to trap and defect states for V BG < V th. In this model, we have taken n 0 = 3 × 1013 m−2, which is similar to ref. 25. With increasing optical power density we have shifted the V th of MoS2 toward left side by ΔV BG comparable to the experimental values (Fig. 3d). To explain the transconductance data of our device in Fig. 3, we need to consider resistances coming from both the individual layers (non-overlapped) as well as the junction part (overlapped). However, the gate response of the individual flakes (non-overlapped) changes less significantly with light (see SI), and hence we consider only the effect of the junction. In the bottom panel of Fig. 5b, we have plotted R C as a function of V BG for different amount of photo-induced doping as shown in Fig. 5b (upper panel). This classical model qualitatively shows the transformation from a dip to no-dip in the modulation of recombination rate by the photo-induced doping.

Fig. 5
figure 5

a Schematic diagram of photo-induced doping process of MoS2 and MoTe2 flakes. b Capacitive model to simulate effect of photo doping on the carrier concentration of individual flakes. Upper panel shows carrier concentration (n) vs. V BG plot for both flakes. For MoS2, n–V BG curves with different V th has been plotted considering its pronounced photo-doping effect. On the other hand, one fixed n–V BG has been plotted for MoTe2, as it shows much less photo-doping effect. In the lower panel, R C –V BG graphs has been plotted for the corresponding MoS2 n–V BG curves. The curves marked by “a” and “b” are used for G eff calculation. c G L as function of V BG for two different V th of MoS2 corresponding to the “a” and “b” n–V BG curves. Inset shows the individual resistance R S and R T as functions of V BG. d G eff as function of V BG. As can be seen G eff captures the dip to peak transition

Full size image

To understand how R C influences the overall transconductance curve, we need to consider the lateral series resistance (R L) coming from the individual flakes at junction, as well as the tunneling resistance (R j), which is inversely proportional to R C. R L is equal to R S + R T, where R S and R T are lateral resistances coming from individual MoS2 and MoTe2, respectively. In Fig. 5c, the inset shows R S and R T as functions of V BG. These have been obtained by fitting the experimental G–V BG curve of MoS2 and MoTe2, respectively (for device D3). Figure 5c shows the plot of total lead conductance G L = (R S + R T)−1 vs. V BG for two different V th of MoS2 (differing by ΔV BG ~2.5 V) corresponding to the curves marked by “a” and “b” in Fig. 5b (lower panel). Please note that Fig. 5c does not capture the dip observed in our experiments. Next, we show the effect on the transconductance by including the series resistance R L along with the tunneling resistance R j. In Fig. 5d, we plot G eff = (R L + R j)−1 as a function V BG corresponding to the same “a” and “b” curves in Fig. 5b. It can be seen that the dip can be qualitatively explained by inclusion of the interlayer recombination rate.

DFT–NEGF calculation

In order to get insights on the charge carrier transport through MoTe2–MoS2 vdW interface, we have also carried out an atomistic study36,37,38,39,40,41 on the two port device structures as illustrated in Fig. 6. As shown in Fig. 6a, the length of the channel region (L) is taken as ~6.6 nm (along the transport direction, i.e., the Z-axis), whereas the MoS2–MoTe2 overlapping distance is maintained as ~2.2 nm (which is 1/3rd of the total channel length). Moreover, along the X-axis (perpendicular to the plane) we incorporate a vacuum region of 15 Å (sufficient to avoid any spurious interaction between periodic images). Here, the left (t_left ~16.57 Å) and the right (t_right ~16.57 Å) electrodes are acting as the semi-infinite reservoirs. Here, after we will call this device structure as vdW interface1. Besides, the zoomed region shown within dotted arrows portrays the top view of the channel of MoS2–MoTe2 vdW interface (having an width ~1 nm). The details of the calculation are given in the SI.

Fig. 6
figure 6

a (top) MoTe2–MoS2 vdW interface, where length of the channel is ~6.6 nm and width is ~1 nm. (bottom) Energy-position resolved LDOS diagram for the vdW interface3. b Transmission spectra of vdW interface1 (upper left), vdW interface2 (upper right), and vdW interface3 (bottom left). (bottom right) The schematic illustrates the formation of electric dipoles along the channel

Full size image

Next, we consider two more variants of the aforementioned device (namely, vdW interface2 and vdW interface3), where the MoS2 and the MoTe2 flakes are of doped with different doping concentrations. In ATK (Atomistix Tool Kit), the effective doping (n-type or p-type) can be achieved by means of incorporating appropriate compensation charge to the system.42, 43 This effective doping scheme (atomic compensation charge) is really advantageous, as it does not depend either on the exact dimensions of the system or on the specific details of the dopant atoms.42 Considering moderate and high doping densities 3.85 × 1017 cm−3 and 1.28 × 1019 cm−3, we set the “atomic compensation charge” values,44 which are equivalent to two-dimensional densities 2.56 × 1014 m−2 and 8.5 × 1015 m−2, respectively. For vdW interface2 and vdW interface3, the MoS2 flakes are n-doped, whereas the MoTe2 flakes are p-doped, with the corresponding “atomic compensation charge” values. It is important to realize that, for any DFT–NEGF simulation, the electrodes act as the carrier reservoirs to maintain equilibrium for the entire system.42 Moreover, taking vdW interface3 into consideration, we find that the energy-position resolved local density of states (LDOS) diagram (as shown in Fig. 6) clearly represents the band alignment of a type-II heterostructure.

Figure 6b illustrates the zero bias transmission spectra of the MoS2–MoTe2 vdW interfaces. It is quite interesting to observe that the transmission spectra obtained for the vdW interface2 and vdW interface3 structures are quite different from that of the vdW interface1. For the intrinsically charge neutralized MoS2 and MoTe2 sheets of vdW interface1, we see no significant dip in states, within the positive energy range of 0 to 2 eV. However, for the samples those are effectively doped into n-type and p-type, we notice the distinct effect of charge separation. The excess negative and positive charge carriers across the individual layers (Fig. 6b, bottom right) give rise to strong interlayer coupling and modulates the transmission states within the range of 0–2 eV. Here, we emphasize on the positive energy transmission states of the individual vdW interfaces. It is worth mentioning that for near-equilibrium electrical current calculation, the states within the bias window ultimately matters. So for any finite bias, the states that are closer to the Fermi energy (E F) will play the dominant role. Nonetheless, it can be seen from Fig. 6b that the states corresponding to V.B.max have further been shifted away from the energy zero (i.e., E−E F = 0) for the vdW interface2 and the vdW interface3. Considering the energy range of 0–2 eV, it is evident from Fig. 6b (upper left) that there will be no anomalous dip in the maximum current (at forward bias) for the vdW interface1. However, this is not the same for other device(s) with excess n-type or p-type carriers. Investigating the transmission spectra, as illustrated in Fig. 6b (upper right and bottom left), we observe clear dips (pointed by arrows) around 1.8 eV. A quantitative calculation of transmission spectra as a function of back gate voltage is, however, beyond the scope of our work at this stage.

To understand the physics behind the atypical nature of the transmission spectra obtained for vdW interface2 and vdW interface3, we propose a plausible explanation. It is known from the literature13 that the excess negative and positive charge carriers across the individual layers (Fig. 6b) make interlayer electric dipoles, which could be the permanent one.13, 14, 45 Nevertheless, this will give rise to a strong interlayer coupling, and perhaps shift-in the trenches of the transmission spectra to the lower-energy range values (which is ~1.8 eV, in this case). Even though both classical and DFT–NEFG calculations qualitatively support our observation, a complete understanding of the transformation of the dip need further theoretical work.

In summary, we demonstrate electrical and opto-electronic measurements on MoTe2–MoS2 vdW heterojunction devices. In normal transconductance measurements, some of the devices showed an anomalous dip in current near the maximum conductance state. We showed that the dip can be modulated with light intensity. We have correlated this anomalous feature within a classical model based on interlayer recombination processes, followed by electrical transport calculations using DFT–NEGF. The first principles-based quantum transport calculation qualitatively capture the anomalous feature depending on the carrier concentration of the individual flakes. Our devices also show large photo response of ~105 A/W at room temperature, which makes it a potential candidate for charge integrating type opto-electronic applications.

Methods

The heterojunction devices were fabricated on Si/SiO2 substrate with 285-nm thick SiO2 layer. The MoS2 and MoTe2 flakes were exfoliated on PDMS and substrate, respectively, from bulk crystal using scotch tape method. To make heterojunction devices, the thinnest flakes were identified with optical microscope. Then Raman and PL spectroscopy was used to sort out single-layer MoS2 and non-contact AFM was used to identify 6–8 layers of MoTe2 flakes. All the AFM characterizations were performed with Park NX10 AFM. After transferring the MoS2 flakes on the MoTe2 flakes, the eletrical contacts were patterned using standard e-beam lithography. Then Ti/Au (5/70 nm) were deposited on the lithography-patterned sample, by thermal evaporation to realize the electrical contacts. The electrical and opto-electronic measurements were performed inside a home-built cryostat, under vacuum of 10−5 mbar at room temperature. For all DC characterization, Keythly 2400 source-meter, Agilent 34401A digital multimeter, and a home-built low-noise current amplifier was used. For opto-electrical measurements, the leds were fixed at ~2 mm distance from the devices. The leds were illuminated with Kythly 2400 in current source mode. The led power was calibrated with PM203 Thorlabs optical power meter.

Data availability

The authors declare that the main data supporting the findings of this study are available within the paper and its SI file. Other relevant data are available from the corresponding author upon request.