Abstract
This study introduces an SIRS compartmental mathematical model encompassing vaccination and variable immunity periods for infectious diseases. I derive a basic reproduction number formula and assess the local and global stability of disease-free and the local stability of the endemic equilibria. I demonstrate that the basic reproduction number in the presence of a vaccine is highly sensitive to the rate of immunity loss, and even a slight reduction in this rate can significantly contribute to disease control. Additionally, I have derived a formula to calculate the critical efficacy period required for a vaccine to effectively manage and control the disease.The analysis conducted for the model suggests that increasing the vaccine’s immunity duration (efficacy) decelerates disease dynamics, leading to reduced rates of reinfection and less severe disease outcomes. Furthermore, this delay contributes to a decrease in the basic reproduction number (\(R_0\)), thus facilitating more rapid disease control efforts.
Similar content being viewed by others
Introduction
Infectious diseases have long been a major public health concern, causing millions of deaths every year. Vaccine development has been a significant step toward preventing the spread of infectious diseases, but vaccine effectiveness can vary depending on factors such as the duration of immunity provided by the vaccine. Mathematical models are effective tools for studying the spread of infectious diseases and assessing the effectiveness of interventions like vaccination.
Several studies have explored SIRS (Susceptible-Infectious-Recovered-Susceptible) disease models with various transmission rates, Several studies have explored SIRS (Susceptible-Infectious-Recovered-Susceptible) disease models with various transmission rates, providing insights into the complex dynamics of infectious diseases within diverse populations. For instance1, analyzed epidemic spreading in complex networks, while2 investigated global stability in multi-group SIRS models with varying population sizes. In3, the global stability of SIRS models with saturation incidence were studied, while4 examined the global stability of SIS, SIR, and SIRS models with density-dependent bilinear incidence. Other works that analysis SIS models are in5 and6. In7, global stability was investigated in an SIRS deterministic model with vaccine and generalized nonlinear incidence, while8 analyzed a stochastic SIVS epidemic model with nonlinear saturated incidence. Additionally, studies by9 and10 investigated the stability of SIRS models with nonlinear incidence, time delay, and temporary immunity. Moreover11, and12 employed Lyapunov functional techniques to analyze the global stability of delayed SIRS epidemic models. These diverse investigations highlight the importance of considering various transmission rates in SIRS disease models to better understand disease dynamics and inform effective control strategies.
Modeling the impact of waning immunity on the transmission of infectious diseases have been considered in literature. In13 the author considered variable latent periods for Tuberculosis, and proved that the qualitative behaviors for the model predicted are similar to those given by the model with an exponentially distributed period of latency. An epidemic model with distributed time delay is derived in14 to describe the dynamics of infectious diseases with varying immunity. According to15, waning immunity shortens inter-epidemic periods and makes disease eradication difficult. In16, a general model is developed to study both immunity loss and immunity boosting, specifically in the context of subclinical infections. Also considers the impact of various assumptions about the nature of immunity. The authors show in17 that moderate waning times (40–80 years) and high levels of vaccination (greater than 70\(\%\)) can cause large-scale oscillations with a large number of symptomatic cases at the peak. In18 the authors show that variable infectivity and recovery rate lead to backward bifurcations under certain conditions for SIRS and SIS models. This makes controlling the disease is more complicated as making the basic reproduction number less than one is not enough to control the disease.
I am motivated by the work19 in which the author considered temporary immunity within a SIRS model when the rate of loss of immunity depend on the time since recovery from disease. The authors conducted the qualitative analysis for this model without considering any form of disease-control intervention. Furthermore, the demographic influence was not taken into account in this study. In this work, I will generalize this model to include, birth, death and vaccination, and examine the impact of demographic characteristics and vaccinations on the qualitative analysis undertaken in that work. In fact, this work can be considered an improving of my research on COVID-1922, where I will explore answers to the following questions: (1) How the waning of immunity affects the epidemic period? (2) How the waning of immunity affects the vaccine effectiveness in controlling the disease? what will be the disease eradication period? (3) How the waning of immunity will affect the vaccine efficacy? (4) Does extending the duration of immunity confer by a vaccine significantly reduce the spread of disease?
The rest of the paper is organized as follows. In section “Formulation of the model” I introduce the mathematical model. In sections “Disease free equilibrium (DFE)” and “Endemic euilibrium (EE)” I discuss the existence and the stability of the DFE for the full model and the existence of the EE for a simplified model using calculated formula for the basic reproduction number. In section “Example of variable immunity losing rate ρ(⊤)” I introduce two simple functions for variable rate of losing immunity and reformulate the basic reproduction number and the mean value for losing immunity. Finally, I conclude with a summary in section “Discussion”.
Formulation of the model
I use a compartmental modeling approach to develop a mathematical model of an infectious disease with a vaccine and a variable immunity period. Specifically, I divide the population into three compartments: susceptible individuals, infected individuals, and recovered individuals.
Variables and parameters
The model divides the population into three groups based on immunity and disease status. The classes are susceptible S(t), infected I(t), and recovered with temporary immune class \(R(t,\tau )\), with \(\tau\) representing the time since recovery or acquiring immunity from vaccination at the moment t.
When susceptibles come into contact with an infected individual, they become infected, and the rate of transmission is \(\beta\). Vaccinated individuals leave the susceptible class to the recovered class at a rate of \(\nu\) (vaccinating rate). Infected individuals recover at \(\alpha\) rates and join the recovered class \(R(t,\tau )\). Recovered individuals may lose immunity at a rate of \(\rho (\tau )\) and fall into the susceptible category. The disease has a \(\gamma\) death rate. The net recruitment rate of individuals to susceptibles is \(\Lambda\) and that determines the population growth. Furthermore, natural death costs \(\mu\).
The model
The ODEs that represent the dynamics in this model are
with the initial conditions \(S(0)=S_0>0\), \(I(0)=I_0>0\), \(R(0,\tau )=0\) and the boundary condition
this equation indicates that individuals who recently recovered from infection or were just vaccinated enter the recovery class with zero time since recovery.
The total population is
Introducing
to be the probability that an immune individual remains immune at time \(\tau\) after recovery. Note that \(P(0)=1\) and will assume that \(\lim _{\tau \rightarrow \infty } P(\tau ) = 0\). Note that the average time to lose immunity is \(\overline{P}=\int _0^\infty P(\tau )d\tau\). Note that in the case \(\rho (\tau )=\rho _1\) constant, I have \(\overline{P}=\frac{1}{\rho _1}\).
Well posedness
Theorem 1
Any solution \((S (t), I(t), R(t, \tau ))\) of the system (1)–(3) with the non-negative initial conditions and the boundary condition (4) is nonnegative and bounded for \(t\ge 0\).
Proof
Solution is nonnegative: For the nonnegativity of I, note that when solving (2), I have For the nonnegativity of \(R(t,\tau )\), I use the characteristic method to find an explicit formula for \(R(t,\tau )\). I have
which is nonnegative for \(t\ge 0\).
which is nonnegative if both S and I are nonnegative. For the nonnegativity of S, I have
which is positive as
This implies that S can’t go below \(S=0\) as it is increasing at this value. Solution is bounded From (8), I have \(\lim _{\tau \rightarrow \infty } R(t, \tau )=0\). Also, when differentiating (5), I have
As a result,
Therefore, if \(N(0)\le \frac{\Lambda }{\mu }\), then \(N(t)\le \frac{\Lambda }{\mu }\) too. \(\square\)
Corollary 1
The set \(\Omega =\left\{ (S,I,R)\in \mathbb {R}_{+}^{3}:,\,\ 0\le S, I, R\le \frac{\Lambda }{\mu }\right\}\) is invariant for the dynamic system (1–3).
Disease free equilibrium (DFE)
To find the DFE, I set \(I=0\), the right hand side of (1) to zero and \(\frac{\partial R}{\partial t}=0\) in (3), then I solve for S and R. Then the DFE is \((S^0,0,R^0(\tau ))\) with
and
with
Here \(e^{-\mu \tau }\) is the probability of staying alive when no disease till time \(\tau\). \(e^{-\mu \tau } P(\tau )\) is the likelihood of staying alive and immune till time \(\tau\). The entire likelihood of natural death for individuals who entered the immune class \(R(t,\tau )\) is represented by Q.
Note that from (5), the total population in this is
It’s important to note that in the absence of a vaccine, the DFE level of susceptible individuals is independent of immunity loss. At the DFE, both the level of infected individuals and recovered individuals are zero. However, if a vaccine is introduced, the levels of both susceptible and recovered individuals will depend on the rate of immunity loss.
Stability of the DFE
I consider small perturbations around the DFE of the form
which, when plugged in (3) and solve for \(z_0\), I have
and when plugged in (1), I have
By inserting (16) into (17), I get
and from (2), I have
The two equations (18) and (19) can be written in matrix form as \(J [x_0\,\,y_0]^T=[0\,\,0]^T\) with
This linear system has none trivial solution if and only if \(\det (J)=0\).
Then first real \(\lambda\) value that makes \(\det (J)=0\) is \(\lambda _1=\beta S^0-(\alpha +\gamma +\mu )\), which is negative if and only if
with \(R_0\) is the basic reproduction number. Other solutions for \(\det (J)=0\) are the zeros for the following function
First, I will prove that the roots of \(F(\lambda )\) are negative for the following special case for \(\rho (\tau )\).
Special case for \(\rho (\tau )\)
Here I discuss a scenario where individuals gain \(100\%\) immunity for a period T and then lose it at a constant rate \(\rho _2\).
with \(\rho _2\) constant. Note that in this case
Also, for \(\lambda \ne -(\mu +\rho _2)\), the function F can be simplified to
and \(F(\lambda ,T)=0\) is equivalent to
or
Note that in case \(T=0\), this polynomial has positive coefficients, therefore two negative roots. As a result for \(T=0\), the DFE is locally asymptotically stable when \(R_0<1\) and unstable for \(R_0>1\).
For \(T>0\)
I define
with \(P_2(\lambda ):=\lambda ^2+ (2\mu +v+\rho _2)\lambda +(\mu +v)(\mu +\rho _2)\) and \(Q_0(T)=-v\rho _2 e^{-\mu T}\)
Considering \(\lambda =\omega i\) with \(\omega >0\) as the purely imaginary roots of the equation \(G(\omega i, T) = 0\), upon substitution of \(\lambda =\omega i\) into the equation \(G(\lambda , T) = 0\) and subsequent separation of the real and imaginary parts, I obtain:
which after solving implies
with the substitution \(\theta =\omega ^2\), then solving the quadratic equation for \(\theta\), I have
since the \(-(2\mu +v+\rho _2)^2+v^2\rho _2^2 e^{-2\mu T}<0\) for \(T>0\). Therefore, \(\theta\) is complex number and no \(\omega >0\) real number exists. From the continuity of \(G(\lambda , T)\) in T, I conclude that all roots for it stay in the left half plane for all T. Therefore, the DFE is locally asymptotically stable for \(R_0<1\) and \(T \ge 0\).
General case for \(\rho (\tau )\)
I need to study the following two cases for \(\lambda\):
Case 1: \(\lambda\) is real number. In this case F satisfies the following
and
Therefore, F can’t have nonnegative \(\lambda\) roots. As a result, the DFE is locally asymptotically stable when \(R_0<1\) and unstable when \(R_0>1\).
Case 2: \(\lambda =u+wi\) complex number. The real component of \(F(\lambda )\) in this case is
As f(u) has no nonnegative roots, \(Re(F(\lambda ))=0\) has no nonnegative roots too. Therefore, if \(\lambda =u+wi\) is a root for F, then \(u< 0\).
Moreover,
Therefore \(\lambda =wi\) is not an eigenvalue and Hopf bifurcation near the DFE is impossible too. To summarize, \(\det (J)=0\) roots include \(\lambda =\lambda _1\) and all other possible eigenvalue satisfies \(Re(\lambda )<0\). In fact, I established the following result:
Theorem 2
The DFE is locally asymptotically stable when \(R_0< 1\) and unstable when \(R_0>1\).
\(R_0\) is the disease threshold amount, which estimates the average number of secondary infections caused by a single infected individual in in a population of susceptibles at a demographic steady state when some susceptible individuals have been vaccinated.
Theorem 3
For the no vaccine case (\(v=0\)) and \(\rho (\tau )\) is bounded for large \(\tau\), the DFE is globally asymptotically stable when \(R_0<1\) and unstable for \(R_0>1\).
Proof
From (12) I have
Now define the following Lyapunov function
with \(m(\tau )=\int _\tau ^\infty \rho (s)e^{-\int _\tau ^s(\mu +\rho (\xi ))d\xi }ds\).
It is clear that \(V|_{DFE}=S^0-S^0-S^0\ln (1)+I^0+\int _0^\infty m(\tau ) *0 d\tau =0\) also
Substitute from (34), I have
To have \(V'(t)<0\), I need \(R_0<1\) when \(m(\tau )\) is chosen such that \(m(0)<<1\). \(\square\)
Endemic equilibrium (EE)
The EE \((S^e,I^e,R^e(\tau ))\) is found by setting the right hand sides of (1, 2) and \(\frac{\partial R}{\partial t}=0\) in (3), then solve for S, I and R. From (2), I have
and from (3)
which when plugged in (1) and solved for \(I^e\), I have
which is positive only for \(R_0>1\).
Note that in this case
It is important to emphasize that the equilibrium level of susceptible individuals (\(S^e\)) is independent of the vaccine and immunity loss, while the equilibrium levels of infected (\(I^e\)) and recovered (\(R^e\)) individuals are dependent on these factors. This EE state indicates that the input and output rates of the susceptible population are balanced, and the effect of the vaccine is not apparent in this case.
Stability of the EE
Considering the following small perturbations around the EE
which when I plug in (3) and solve for \(z_0\), I have
and from (1), I have
with
Now, plug in (38) in (39), I have
Also, from (2), I have
with
as \(-\beta S^e+\mu +\alpha +\gamma =0\). Therefore, (41) is reduced to
Therefore, the system (40) and (42) can be written on the matrix for \(M[x_0\,\,y_0]^T=[0\,\,0]^T\), with
This system has nontrivial solution \([x_0\,\,y_0]^T\ne [0\,\,0]^T\), if and only if \(F(\lambda ):=\det (M)=0\) with
in which
with \(Q^*(0)=Q\). Note that integration by parts was done here.
I need to study the following two cases:
Case 1: \(\lambda\) is real number.
Note that for \(\lambda \ge 0\) and \(R_0>1\)
therefore \(F(\lambda )\) has no nonnegative roots.
Case 2: \(\lambda =u+wi\) is complex number.
The matrix \(M=A+Bi\) with
Again to have nontrivial solution I need both \(\det (A)=\det (B)=0.\) Introducing the function \(Q_c(u,w)\) and \(Q_s(u,w)\), with
If \(R_0>1\), \(\det (A)=0\) only for \(u\le 0\).
since \(w\ne 0\), I must have
which leads to \(w=-e^{-(u+\mu )\tau }\sin (w \tau )\). In sum, regardless of w value I must have the real part of the eigenvalue u negative.
In the following theorem I use \(R_0\) to describe the stability of the DFE
Theorem 4
The EE exists and is locally asymptotically stable if and only if \(R_0>1\).
In sum, I noted that without a vaccine, \(R_0\) is independent of immunity loss. Moreover, if \(R_0<1\), then all solutions will converge to the same DFE point, but possibly with increasing oscillations as the delay increases. If \(R_0>1\) regardless of the presence of a vaccine, then all solutions will converge to the same level of susceptible individuals, but different levels of infected and recovered individuals that depend on the rate of immunity loss.
Example of variable immunity losing rate \(\rho (\tau )\)
Step function
Here, I discuss a scenario where individuals gain partial immunity after recovering from an infection or receiving a vaccination. This immunity lasts for some time T before gradually decreasing. To represent this, we utilize a step function, chosen for its approximation purposes despite lacking a direct biological interpretation. This simplifies the calculations and provides necessary approximations.
Note that in case of considering
In this case, from (6), I have
and the mean value for losing immunity is
Moreover, from (13) I have
When \(T\rightarrow \infty\), then I have \(\overline{P}\rightarrow \frac{1}{\rho _1}\), and \(Q\rightarrow \frac{1}{\mu +\rho _1}\). Also, from (20) I have
Note that for the special case \(\rho _1=0\), \(\overline{P}=T+\frac{1}{\rho _2}\) and \(Q=\frac{1}{\mu }\Big (1-e^{-\mu T}\Big )+\frac{1}{\mu +\rho _2}e^{-\mu T}\).
Critical efficacy period \(T_c^*\)
Note that \(R_0<1\) is equivalent to
To give the inequality (46) more meaning, I define \(T_c^*(\rho _2)=\lim _{\rho _1 \rightarrow 0}T_c(\rho _1, \rho _2)\), that is the lowest efficacy period for vaccine needed to control the disease. Here
Linear function
with \(\rho _0\) constant. In this case \(P(\tau )=e^{-\frac{\rho _0\tau ^2}{2}}\) and the mean value for losing immunity is \(\overline{P}=\sqrt{\frac{\pi }{2\rho _0}}\).Moreover, \(Q=\sqrt{\frac{\pi }{2\rho _0}}e^{\frac{\mu ^2 }{2\rho _0}}\). Note that \(\frac{dR_0}{dQ}<0\) and \(\frac{dQ}{d\rho _0}<0\), which implies \(\frac{dR_0}{d\rho _0}=\frac{dR_0}{dQ}\times \frac{dQ}{d\rho _0}>0\) . In sum, \(R_0\) is increasing function in \(\rho _0\), the slope of \(\rho (\tau )\) in this case.
Sensitivity of \(R_0\) to parameters changes
Given the uncertainty in parameter values, I conducted a comprehensive analysis of various parameter ranges to understand how changes in parameters affect the model’s \(R_0\) value. The parameter ranges are presented in Table 1, indicating the 95\(\%\) confidence intervals for the estimated parameter values obtained from the two cited references. To do this, I used Latin Hypercube sampling and partial rank correlation coefficients (PRCCs) to identify which parameters have the greatest impact on \(R_0\) [?]. Latin Hypercube Sampling is a statistical method that helps us explore how an outcome variable reacts to changes in input variables. PRCCs allow us to measure the relative sensitivity of each parameter, regardless of whether it increases or decreases the outcome variable.
In Fig. 1, the graph illustrates the PRCCs for each input parameter. This visual representation clearly highlights that \(R_0\) is most influenced by variations in five key parameters: the transmission rate (\(\beta\)), the rate of losing immunity (\(\rho\)), the recovery rate (\(\alpha\)), the disease-induced death rate (\(\gamma\)), and the vaccinating rate (\(\nu\)). This underscores that effective disease control hinges on maintaining a low transmission rate, a reduced rate of immunity loss, and elevated rates of disease-induced death, recovery, and vaccination. Intriguingly, even slight adjustments in the values of \(\beta\), \(\rho\), and \(\nu\) can shift \(R_0\) from above one to below one, emphasizing their substantial impact on the dynamics of \(R_0\), as demonstrated in Fig. 2.
Estimation of time series solution
Simulating disease dynamics in the absence of vaccination can serve as a baseline for comparing the impact of vaccination strategies. Also, simulating the effect of varying the duration of immunity provided by the vaccine can also assist in determining the minimum duration of immunity required to control the disease. The parameter values and the initial conditions will be taken from the Table 1 and the Table 2.
The discretization of the model (1)–(3) is conducted as follows: I employ a forward difference for the time derivatives in the equations, and a centered difference for the age derivative. Here, I set \(\Delta t=0.01\) and \(\Delta \tau =0.1\), with \(\frac{\Delta t}{\Delta x}<1\) in this case. \(t_i=i*\Delta t\) for \(i=0,1,\ldots 1000\) and \(\tau _j=j \Delta \tau\) for \(j=0,1,\ldots ,30,000\). The time span extends from 0 to 300, with the period since recovery spanning from 0 to 100. The code has been implemented in MATLAB and a samples codes are included in the supplementary information of this work.
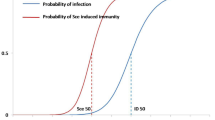
I generate a time series solution for the model without vaccination, as shown in Fig. 3. The value of \(\rho (\tau )\) was set to 0.03, and also to the function \(\rho (\tau )=0.03 u(\tau -50)\) with \(u(\tau )\) the unit step function, which has the same constant value but with a 50-days delay. The resulting value of \(R_0\) was found to be 6.0157 in both cases. Our analysis indicates that delaying the loss of natural immunity by 50 days leads to a lower number of infected individuals and a higher number of individuals in the recovered class. Additionally, the phase portrait depicting the relationship between S(t) and I(t) as shown in the Fig. 4 for various delays in the loss of immunity rate \(\rho (\tau )=0.03 u(\tau -T)\) for \(T=0,25,50,75\). In scenarios without vaccination, when there’s a delay in losing immunity, the disease dynamics slow down in reaching the EE. This delay results in a higher number of recovered individuals at the EE level, potentially saving lives by reducing the likelihood of reinfection.
In Fig. 5, I conducted the simulation again with a vaccine rate \(v=0.5\). Our results showed \(R_0=0.1575\) for the delayed loss of immunity \(\rho (\tau )=0.03u(\tau -50)\) with \(u(\tau )\) the unit step function. Additionally, I observed an \(R_0=0.3410\) for the constant loss of immunity rate \(\rho (\tau )=\frac{1}{30}\). These findings support the idea that delayed loss of immunity leads to a significant decrease in the number of infected individuals and an increase in the number of recovered individuals. Also, when this supports the state forward idea that a longer duration of immunity gained through vaccination makes the vaccine more effective in controlling the disease. Furthermore, the phase portrait illustrating the correlation between S(t) and I(t) can be seen in Fig. 6, with different delays in the loss of immunity rate \(\rho (\tau )=0.03u(\tau -T)\) for \(T=00,25,50,75\). \(R_0=0.3410,0.2153, 0.1575,0.1300\) respectively. In scenarios with vaccination, when there’s a delay in losing immunity: the more the delay in losing immunity the smaller the \(R_0\) and the faster the disease is controlled. Also, the same implies higher number of recovered immune individuals at the DFE level and the lower the susceptibles, potentially saving more lives by reducing the likelihood of reinfection.
To demonstrate the rule of the vaccine in controlling the disease, we compare Figs. 3 (vaccine \(v=0\)) and 5 (vaccine \(v=0.5\)). With the same rate of immunity loss, it is evident that the number of susceptible Figure (a) and infected Figure (b) individuals is higher in the long run for the no-vaccine case compared to the vaccine case (converges to \(I=0\)). Also, the number of recovered individuals in the long run is significantly lower in Fig. 3d compared to Fig. 5d. This observation indicates that the vaccine not only reduces the number of susceptible individuals and completely eradicates the infected individuals but also increases the number of recovered individuals, thereby saving many lives.
In order to confirm our results, I repeated the simulation using the linear function \(\rho (\tau )=0.0006\tau\) with \(\tau \in [0,100]\) along with its average value of \(\rho (\tau )=0.03\) over the same interval. The results are shown in Fig. 7. Significant differences exist between the two results, emphasizing the importance of using partial differential equations for the recovered population, as they account for the delay caused by the variable rate of immunity loss. It’s important to note that in cases of constant average rates of immunity loss, the disease tends to be more severe due to the higher \(R_0\) value. This likely results in more people getting reinfected, leading to increased fatalities.
Comparison of time series solutions for the no-vaccine case (\(v=0\)) with constant rate \(\rho (\tau )=0.03\) and the step function rate \(\rho (\tau )=0.03u(\tau -50)\) for losing immunity, including: (a) proportions of susceptible individuals, (b) proportions of infected individuals, (c) proportions of recovered individuals R(t) and \(\int _0^{100} R(t,\tau )d\tau\). Finally in (d) The proportions of recovered individuals \(R(\tau ,t)\) for the step function scenario. In both scenarios, we have \(R_0=6.0157\), and the solutions converge to the equilibrium points: EE \((S^e,I^e,R^e)=( 0.1662,0.3961,0.4377)\) for the constant rate and to the EE \((S^e I^e,\int _0^\infty R^e(\tau )d\tau )=(0.1662,0.1456,0.6882)\) for the step function.
S–I phase portrait for the step function \(\rho (\tau )=\frac{1}{30}u(t-T)\) for \(T=0,25,50,75\) for the no vaccine case (\(v=0\)). Here \(R_0=6.0157\). The solutions converge to the EE \((S^e, I^e,R^e)= (0.1662,0.3961,0.4377), (S^e, I^e,\int _0^\infty R^e(\tau )d\tau )=(0.1662, 0.2990,0.5348), ( 0.1662,0.1456,0.6882), (0.1662,0.0521,0.6257)\) respectively.
Comparing the time series solutions for the constant rates \(\rho (\tau )=0.03\) and for the step function \(\rho (\tau )=0.03u(\tau -50)\) of losing immunity in the vaccine case (\(v=0.5\)). I have (a) The proportions of susceptible individuals, (b) the proportions of infected individuals. (c) The proportions of recovered individuals \(R(\tau ,t)\) for the step function scenario. (d) The proportion of recovered R(t) and \(\int _0^{100} R(t,\tau )d\tau\). Here, with \(R_0 =0.3410\) and \(R_0=0.1575\) , for the log run, the solution converges to DFE \((S^0,I^0,R^0)=(0.0910,0,0.9090)\) and the DFE \((S^0, I^0,\int _0^\infty R^0(\tau )d\tau )=(0.0429,0.0000,0.9571)\) respectively.
S–I phase portrait for the step function \(\rho (\tau )=\frac{1}{30}u(t-T)\) for \(T=0,25,50,75\) for the vaccine case (\(v=0.5\)). Here \(R_0=0.3410,0.2153, 0.1575,0.1300\) and the solutions converge to the DFE \((S^0, I^0,R^0)=(0.0910,0,0.9090)\), and to the DFE \((S^0, I^0,\int _0^\infty R^0(\tau )d\tau )=(0.0653,0.0000,0.9347),(0.0429,0.0000,0.9571), (0.0216,0.0000,0.9784)\) respectively.
Comparing the model’s time series solutions for the linear rate of losing immunity \(\rho (\tau )=0.0006\tau\) and its average value \(\rho (\tau )=0.03\) over the time interval \(\tau \in [0,100]\) . Here, the vaccination rate is set to \(v=0.5\). The graph illustrates: (a) The proportions of susceptible individuals, (b) the proportions of infected individuals, (c) the proportions of individuals who have recovered from the disease with the linear rate of immunity loss , and (d) the average of recovered \(\overline{R}(t)=\int _0^{100} R(t,\tau )d \tau\) in the linear rate case, and the recovered rate R(t) in the case of the average rate. Here, with \(R_0=0.2330\) and \(R_0 =0.3410\), for the log run, the solution converges to the DFE \((S^0, I^0,\int _0^\infty R^0(\tau )d\tau )=(0.0387, 0.0000, 0.9433)\) and the DFE \((S^0,I^0,R^0)=(0.0567, 0.0000,0.9613)\) respectively.
For \(R_e>1\), \(S^e\) is independent of the vaccine
In Fig. 8, we apply the model with \(\beta =0.6\) to ensure that \(R_0>1\) when \(v\ne 0\), specially when \(v=0.1\) and \(v=0.4\) . The model is applied with a constant rate of losing immunity, \(\rho =0.03\). We found that the time series solution converges to the EE and \(S^e\) in both cases equals the theoretical value \(S^e=\frac{\alpha +\gamma +\mu }{\beta }=0.0554.\)
Comparing the time series solutions for vaccine rates \(v=0.1\) and \(v=0.4\) with a constant rate of losing immunity (\(\rho =0.03\)), I observed the following: (a) The proportions of susceptible individuals. (b) The proportions of infected individuals. (c) The proportions of recovered individuals. Here, with \(R_0 =18.0470\) and \(R_0=1.2609\) , the long-run solution converges to the EE \((S^e,I^e,R^e)=(0.0554,0.4487,0.4958)\) and \((S^e, I^e,R^e)=(0.0554,0.0983,0.8463)\) respectively.
Discussion
I have developed an SIRS model for infectious diseases incorporating vaccination and variable immunity periods. This model combines two ordinary differential equations (ODEs) and one partial differential equation (PDE). I have derived formulas for the basic reproduction number, the disease-free equilibrium, and the endemic equilibrium. Through small perturbation analysis, I have demonstrated that the disease-free equilibrium is globally asymptotically stable when \(R_0<1\) and unstable when \(R_0>1\). Additionally, I have proven the existence and local asymptotic stability of the endemic equilibrium for \(R_0>1\).
Furthermore, I have explored two simple variable immunity loss rates: the step function and linear function. For the step function rate, I have obtained a formula for \(R_0\) and shown that its limit reduces to the conventional \(R_0\) for the classical SIRS ODEs model with a constant rate of immunity loss. Moreover, I have derived a formula to determine the critical efficacy period required for any a given vaccine to effectively control the disease.
I have utilized sensitivity analysis to demonstrate that \(R_0\) is highly sensitive to variations in several critical parameters, including transmission rate, immunity loss rate, recovery rate, disease-induced death rate, and vaccination rate. It has been revealed that maintaining low transmission rates, minimizing immunity loss, and increasing recovery and vaccination rates are crucial for effective disease control. Even minor adjustments in these parameters can significantly influence the value of \(R_0\), underscoring their crucial role in mitigating disease spread.
The simulation conducted for the model indicates that delaying the loss of immunity slows down disease dynamics, whether or not a vaccine is present, resulting in lower reinfection rates and reduced disease severity. Moreover, this delay decreases the basic reproduction number (\(R_0\)), facilitating faster disease control. Furthermore, fixing the rate of immunity loss, we have demonstrated that the vaccine similarly affects the basic reproduction number (\(R_0\)), leading not only to a reduction in the number of susceptible and infected individuals but also to an increase in the number of recovered individuals, thereby saving many lives.
Conclusion
In summary, this study emphasizes the significance of accounting for delays in immunity loss when modeling infectious diseases. The delay in losing immunity slows down disease dynamics, regardless of vaccine involvement, thereby decreasing the risk of reinfection. This delay also contributes to reducing \(R_0\) in the presence of vaccination, potentially leading to faster disease control. The vaccine similarly reduces \(R_0\), the number of susceptible and infected individuals, and increases the number of recovered individuals. If the vaccine provides a long-lasting immunity period, it can further expedite disease control. These findings have significant implications for designing effective vaccination programs and public health policies, especially in light of the potential extension of immunity periods offered by future vaccines.
This study has some limitations. Future research could enhance the model by integrating additional factors, such as the influence of asymptomatic individuals or the effects of vaccine efficacy on disease transmission dynamics. Moreover, it’s crucial to recognize that individuals of different ages may encounter diverse rates of vaccine immunity loss.
Data availability
All data generated or analysed during this study are included in this published article [and its supplementary information files].
References
Li, C. H., Tsai, C. C. & Yang, S. Y. Analysis of epidemic spreading of an SIRS model in complex heterogeneous networks. Commun. Nonlinear Sci. Numer. Simul. 19, 1042–1054 (2014).
Muroya, Y., Enatsu, Y. & Kuniya, T. Global stability for a multi-group SIRS epidemic model with varying population sizes. Nonlinear Anal. Real World Appl. 14, 1693–1704 (2013).
Hao, L., Jiang, G., Liu, S. & Ling, L. Global dynamics of an SIRS epidemic model with saturation incidence. Biosystems 114, 56–63 (2013).
Vargas-De-León, C. On the global stability of SIS, SIR and SIRS epidemic models with standard incidence. Chaos Soliton. Fract. 44, 1106–1110 (2011).
Berhe, H. W. & Al-arydah, M. Computational modeling of human papillomavirus with impulsive vaccination. Nonlinear Dyn. 103(1), 925–946 (2021).
Madhu, K. & Al-arydah, M. Optimal vaccine for human papillomavirus and age-difference between partners. Math. Comput. Simul. 185, 325–346 (2021).
Lahrouz, A., Omari, L., Kiouach, D. & Belmaâti, A. Complete global stability for an SIRS epidemic model with generalized non-linear incidence and vaccination. Appl. Math. Comput. 218, 6519–6525 (2012).
Zhao, D., Zhang, T. & Yuan, S. The threshold of a stochastic SIVS epidemic model with nonlinear saturated incidence. Phys. A 443, 372–379 (2016).
Qi, L. & Cui, J. A. The stability of an SEIRS model with nonlinear incidence, vertical transmission and time delay. Appl. Math. Comput. 221, 360–366 (2013).
Xu, C. & Li, X. The threshold of a stochastic delayed SIRS epidemic model with temporary immunity and vaccination. Chaos Soliton. Fract. 111, 227–234 (2018).
Xu, R., Ma, Z. & Wang, Z. Global stability of a delayed SIRS epidemic model with saturation incidence and temporary immunity. Comput. Math. Appl. 59, 3211–3221 (2010).
Enatsu, Y., Nakata, Y. & Muroya, Y. Lyapunov functional techniques for the global stability analysis of a delayed SIRS epidemic model. Nonlinear Anal. Real World Appl. 13, 2120–2133 (2012).
Feng, Z., Huang, W. & Castillo-Chavez, C. On the role of variable latent periods in mathematical models for tuberculosis. J. Dyn. Differ. Equ. 13, 425–452 (2001).
Blyuss, K. B. & Kyrychko, Y. N. Stability and bifurcations in an epidemic model with varying immunity period. Bull. Math. Biol. 72, 490–505 (2010).
Gomes, M. G., White, L. J. & Medley, G. F. Infection, reinfection, and vaccination under suboptimal immune protection: Epidemiological perspectives. J. Theor. Biol. 228(4), 539–49 (2004).
Glass, K. & Grenfell, B. T. Antibody dynamics in childhood diseases: Waning and boosting of immunity and the impact of vaccination. J. Theor. Biol. 221(1), 121–31 (2003).
Heffernan, J. M. & Keeling, M. J. Implications of vaccination and waning immunity. Proc. Biol. Sci. 276(1664), 2071–80 (2009).
Kribs-Zaleta, C. M. & Martcheva, M. Vaccination strategies and backward bifurcation in an age-since-infection structured model. Math. Biosci. 177–178, 317–32 (2002).
Bhattacharya, S. & Adler, F. R. A time since recovery model with varying rates of loss of immunity. Bull. Math. Biol. 12, 2810–9 (2012).
de León, U. A., Avila-Vales, E. & Huang, K. L. Modeling COVID-19 dynamic using a two-strain model with vaccination. Solitons Fract. 157, 111927 (2022).
Al-arydah, M., Berhe, H., Dib, K. & Madhu, K. Mathematical modeling of the spread of the coronavirus under strict social restrictions. Math. Meth. Appl. Sci. 2021, 1–11 (2021).
Al-arydah, M. Mathematical modeling and optimal control for COVID-19 with population behavior. Math. Meth. Appl. Sci. 46, 19184–19198. https://doi.org/10.1002/mma.9619.AL-ARYDAH19198 (2023).
Acknowledgements
The author thank the reviewers for their valuable comments and suggestions, which have greatly improved this manuscript.
Author information
Authors and Affiliations
Contributions
All the work have been done by one author.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Al-arydah, M. Assessing vaccine efficacy for infectious diseases with variable immunity using a mathematical model. Sci Rep 14, 18572 (2024). https://doi.org/10.1038/s41598-024-69651-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-69651-6
- Springer Nature Limited