Challenges to extracting spatial information about double P dopants in Si from STM images

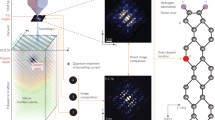
Abstract

The design and implementation of dopant-based silicon nanoscale devices rely heavily on knowing precisely the locations of phosphorous dopants in their host crystal. One potential solution combines scanning tunneling microscopy (STM) imaging with atomistic tight-binding simulations to reverse-engineer dopant coordinates. This work shows that such an approach may not be straightforwardly extended to double-dopant systems. We find that the ground (quasi-molecular) state of a pair of coupled phosphorous dopants often cannot be fully explained by the linear combination of single-dopant ground states. Although the contributions from excited single-dopant states are relatively small, they can lead to ambiguity in determining individual dopant positions from a multi-dopant STM image. To overcome that, we exploit knowledge about dopant-pair wave functions and propose a simple yet effective scheme for finding double-dopant positions based on STM images.

Introduction

Precise spatial placement of phosphorous dopants in silicon is essential for fabricating atom-scale quantum devices in silicon with potential applications in quantum computing¹ and quantum simulation². Dopant placement is achieved via hydrogen-based lithography, allowing dopants to be located in small patches of dangling (unpassivated) bonds, formed on the silicon surface with a scanning tunneling microscope (STM), and then covered by a protective silicon overgrowth. At the current stage of technology, neither the dopant position nor the number of dopants in a patch can routinely be controlled precisely enough. Detailed knowledge of the dopant positions in a fabricated device is necessary to understand the connection between device performance and dopant arrangement when aiming at systems of dopants, coupled dopants, and dopant clusters in chains and arrays^2,3. As demonstrated in recent works^4,5,6,7, the position of a single buried P dopant close to a Si surface can be determined from the structure of its STM image⁴. However, modeling this structure is far from trivial and often ambiguous⁸, even for a single dopant. Moreover, STM imaging of buried dopants needs to be extended to study multi-dopant structures^1,2, presenting further challenges. Such STM image simulations, obtained with a machine learning approach⁵, have been presented recently. A more fundamental understanding of imaging multi-dopants is needed.

Double dopants are the simplest multi-dopant structures. In fabricated device structures, double-dopant structures in various unintended spatial configurations are expected to occur when another specific double-dopant structure is the intended target and even when single dopants and multi(more than two)-dopants are the intended targets. Coupled, P dopant pairs buried in Si are a solid-state analog to diatomic molecules⁹. This should provide a context for building a better understanding. However, unlike real diatomic molecules, double-dopant artificial molecules in Si will be fabricated with different separations and placement in the host crystal lattice. There will be many versions of the same double-dopant pair that must be imaged and identified. Moreover, the simple picture of a double dopant as a diatomic molecule is further complicated by the valley physics of the Si host, leading to strong oscillatory behavior of exchange integrals that couple the pair⁹.

Here, we present the results of atomistic calculations for nearly two thousand random placements of P dopant pairs in the Si host. The quasi-molecular wave function of the double dopant is then decomposed in the basis of wave functions of the two single-dopants that make up the pair. This analysis reveals that the simple picture of a double-dopant ground state understood in terms of a symmetric combination of uncoupled-dopant ground-state wave functions often fails, especially, but not only, for closely spaced dopants, due to non-negligible contributions from higher excited, single-dopant levels. This picture gets further complicated for double-dopant systems near the Si surface, as in fabricated, experimental devices. This, in turn, leads to a situation where the STM-image simulation based on combining contributions from the images of two single-dopants fails to describe a double-dopant STM image. Thus, when using a simple model involving only the single-dopant ground states, the complicated quasi-molecular character of double-dopant states produces ambiguity in determining multi-dopant positions from STM images. However, when we extend the model to account for the first excited, dopant states, combined with additional optimizations discussed in the text, we overcome this problem. We propose a conceptually simple and computationally efficient yet effective algorithm to determine double-dopant positions from their STM images.

Results

Figure 1

Expansion of a double-dopant representation in the basis obtained by orthogonalizing representations of the first n eigenstates of both dopants (2n eigenstates in total). The horizontal axis represents the distance between dopants in lattice constants. The vertical axis represents the squared coefficients of the linear combination that best matches the double-dopant representation. The representation used here corresponds directly to the tight-binding coefficients. Both dopants are placed far away from the surface, near the center of the computational box. Although we show expansion in the basis of all considered (12) single dopant states, the results are dominated by e1 and e2–e6 states.

To understand how well the double-dopant STM image can be represented by a combination of the STM images of the two dopants, we first investigate how well the double-dopant ground-state wave function can be represented by the symmetric combination of the ground-state wave functions of the two (uncoupled) single-dopants. In Fig. 1, we show the double-dopant ground state decomposition into single (uncoupled) P dopant, orthogonalized, wave function components as a function of the inter-dopant separation distance (see “Methods”) for 561 different, random realizations of the double dopant corresponding to different spatial placements of P dopants buried in the Si host. The double-dopant ground-state wave function ${|{\Psi _0}\rangle }$ is strongly dominated by contributions from ground states of separate dopant wave functions (${\langle {\Psi _0|\varphi _1^\prime }\rangle }^2$ and ${\langle {\Psi _0|\psi _1^\prime }\rangle }^2$, where $\varphi _1^\prime$ and $\psi _1^\prime$ are the single-dopant contributions and $^\prime$ indicates the orthogonalized single dopant wave functions) altogether reaching close to 100% for large inter-dopant separations. Such a result strongly supports understanding a double-dopant wave function in terms of a simple combination of two ground-state dopant orbitals of A symmetry (e1 points in Fig. 1).

However, for reduced inter-dopant distance, contributions from these lowest components get reduced, typically varying from 75% to 95% for distances between 6 to 10 lattice constatns (l.c.) (i.e., 3.25 to 5.43 nm). At this range of inter-dopant distances, a non-negligible contribution from excited single-dopant states T$_2$ (e2, e3, and e4) and E (e5, e6) starts to emerge, reaching over 20% in several cases.

We note that the contributions from the 2s manifold of single-dopant states (e7…e12) do not play a significant role in any considered cases, although these states are important for many-body properties of dopant^10,11, and are studied here for completeness.

For even lower inter-dopant spacing (below 3 l.c. or 1.6 nm), single-dopant ground-state contributions can be as low as 65-70%. Moreover, the decomposition of the quasi-molecular wave function into all considered (e1…e12) components reaches only about 95% of the total wave function. Therefore, even higher (3s, 4s, …) single-dopant multiplets would be necessary to decompose the double-dopant wave function into single-dopant states completely. However, the possibility of performing such analysis was constrained by the intrinsic limits of eigenvector solvers available to us (see the “Methods”).

Figure 2

(Top row) Total charge on planes perpendicular to the [110] direction plotted as a one-dimensional charge density along the [110] line for the six lowest states of a system with two uncoupled single-dopants placed at $\left( -4.5,-1.0,0.5\right)$l.c. and $\left( -0.75,3.75,-0.25\right)$l.c.. This one-dimensional charge density is found by summing the squares of LCAO coefficients over all atomic sites on each plane perpendicular to a line in the [110] direction. Each dopant sits on one of these planes. The plane that passes through the midpoint between the dopants is chosen to be the plane at zero. (Middle row) One-dimensional charge density of a double-dopant ground state $\left| \Psi _{12}\right| ^2$ from a full tight-binding calculation compared with idealized linear combination $\left| \Psi _{LC}\right| ^2$ involving single-dopant ground states only; dopants are separated by 3.31 nm, $\left| \Psi _{LC}\right| ^2$ matches only 80% of $\left| \Psi _{12}\right| ^2$. (Bottom row) Comparison of $\left| \Psi _{12}\right| ^2$ (left) and $\left| \Psi _{LC}\right| ^2$ (right) shown as a 2D plot. The two-dimensional densities at points P in the plane are the charges summed over all sites on the [001] line passing through P and shown at P on the (001) plane.

Figure 3

(Top row) One-dimensional charge densities plotted along the [100] line for the six lowest states of the system of two uncoupled single-dopants located at $\left( 5.00,2.00,1.00\right)$l.c, and $\left( -0.75,0.75,-0.25\right)$l.c.. The one-dimensional densities are shown along the [100] direction as the sum of the charge on each plane perpendicular to [100]. (Middle row) The one-dimensional charge density of a double-dopant ground state $\left| \Psi _{12}\right| ^2$ from a full tight-binding calculation compared with idealized linear combination $\left| \Psi _{LC}\right| ^2$ involving single-dopant ground states only; dopants are again separated by very similar distance (3.27 nm), but one of the dopants is placed differently within the unit cell position compared to Fig. 2, $\left| \Psi _{LC}\right| ^2$ now matches over 90% of $\left| \Psi _{12}\right| ^2$. (Bottom row) Comparison of $\left| \Psi _{12}\right| ^2$ and $\left| \Psi _{LC}\right| ^2$ shown as a 2D plot illustrating different spatial alignment of double dopants compared to Fig. 2, but with very similar inter-dopant distance. Again, the two-dimensional densities are the charges summed over all atomic sites along the [001] line through the point and shown on the (001) plane.

To investigate the problem further, Figs. 2, and  3 show the charge densities for an inter-dopant distance of approximately 3.3 nm (6 l.c.), corresponding to the two extreme cases for overlap with the linear combination of single-dopant ground states of 80% and 90% displayed in Fig. 1 for that dopant separation. In the top row of each figure, the charge densities of the individual uncoupled dopants are shown. The ground state A$_1$ (e1), T$_2$ (e2, e3, e4), and E (e5, e6) states are shown. The T$_2$ and E states have similar densities. The A$_1$ states are less spread out. These figures also compare the full tight-binding (TB) calculation involving two coupled dopants ($\Psi _{12}$) with the model assuming a linear combination of individual ground states of dopants only ($\Psi _{LC}=\alpha \varphi _1+\beta \psi _1$, with $\alpha$ and $\beta$ obtained by fitting to a full model). Notably, both cases (Figs. 2 and  3) have very similar inter-dopant spacing (3.27 vs. 3.31 nm), differing by only 0.4 Å (related to a different dopant placement within the unit cell). In Fig. 3, the simplified model produces a small residual difference between the two approaches. However, Fig. 2 shows notable differences both in 1D (middle row) and in 2D (bottom row) plots. The difference is manifested in both the charge density plots in the region between the dopants and in the (squared modulus) wave-function difference between the two models. The susceptibility of various properties⁹ of a double-dopant system to small changes of atomic position is a known phenomenon resulting from the complicated multi-valley character of dopant wave-functions. Here, it manifests itself by leading to the more complicated character of the quasi-molecular double-dopant wave function. In some cases, the double-dopant wavefunction can be well described by a linear combination ($\alpha \varphi _1+\beta \psi _2$) of single dopant functions. This approximation is, however, inadequate in other cases (with nearly the same inter-dopant separation). In both figures, the difference between the charge densities of the simplified model and the full TB calculation is small at the dopant sites. However, the (square-modulus) wave-function difference can be significant at the dopant sites, again showing the complicated valley effects on the wave-function interference. Fig. 2 illustrates that even a relatively large (80%) contribution of single ground dopant states to a full double-dopant wave-function may produce a notably different outcome should other terms be neglected.

This will profoundly impact understanding double-dopant STM pictures, as discussed later. More generally, this means that higher energy single-dopant states must be accounted for in the modeling on equal footing with single-dopant ground states. The importance of higher single-dopant levels is also apparent in many-body studies of dopant charging energies^10,11. The importance of excited single-dopant states is also consistent with the recent work of one of our coauthors¹² that presented calculations of dopant pairs, including inter-orbital couplings of excited single-dopants. The knowledge of coupling between various pairs of orbitals will also be essential for constructing multi-orbital models (such as a Hubbard model) for chains and arrays of multiple donors, thus going far beyond the context of STM simulations.

Figure 4

Linear combination analysis similar to Fig. 1, with both dopants placed close to a reconstructed and hydrogen-passivated Si surface.

Near-surface dopants

The deep-buried dopant cases considered so far provide a better, more fundamental understanding of dopants in Si. However, in dopant-based quantum devices that STM can image, the dopants must be shallow-placed donors just below the surface and can be affected by surface proximity. Therefore, in Fig. 4, we repeat the analysis presented in Fig. 1. However, here, we performed the calculations for 1128 random placements of dopant pairs at most 3 l.c. (16.3 nm) below the $2\times 1$ (dimer) reconstructed and hydrogen-passivated Si surface.

As shown in Fig. 4, the surface substantially modifies the wave-function character of quasi-molecular double-dopant ground states. Here, even for the large inter-dopant distance of 5 nm considered, A$_1$ components comprise from 75% to 95% of the double dopant wave function, with most results grouping between 80% and 90%. Moreover, because the presence of surface breaks the bulk symmetry, one of the T$_2$ states (e2 in Fig. 4) makes an important contribution, reaching up to approximately 10% to 15%. (We emphasize that states of dopants close to the surface no longer possess exact bulk A, T, or E symmetry.) Since this decomposition is performed with a basis defined by single, shallow dopants, the proximity of the surface modifies not only single-particle contributions to dopant states but also the basis expansion (spectral composition) of double-dopant states.

STM image relevance

Figure 5

Linear combination analysis similar to Fig. 1. Here, the dopants are placed near the top hydrogen-passivated surface of the computational box, and the values of the STM-like functional of the wave function (on the 2D image plane) near the top surface are used as the representation instead of the linear combination of dopant orbitals.

From the eigenstate decomposition, we know that the largest contributions to the double-dopant quasi-molecular ground-state wave function typically are the A$_1$ terms originating from the single-dopant wave functions. Based on the above, one could expect that STM image simulation of a double-dopant system could be adequately reconstructed from two single-dopant A$_1$ wave functions. However, Fig. 5 shows this may not necessarily be true. To simulate an STM image from a dopant wave function, following Chen’s¹³ approach, the STM image is effectively created as a functional of the wave function on a plane above the Si surface. STM images strongly depend on the orbital character of the STM^4,8 tip. Specifically, the STM image is built on a plane at the tip distance from the Si top surface and is obtained by combining contributions for s, p, and d tip-orbitals (see the “Methods” section). In particular, the contribution of p and d tip orbitals can and will affect the resulting pictures significantly^4,8. Here, we take the tip composition with a notable contribution from p and d orbitals, as this combination has been found in our previous work⁸ to reproduce very well the experimental STM image of a single dopant.

Figure 6

Schematic representation of the analysis. The results of tight-binding calculations are converted to one of two representations: either coefficients of the wave function in tight-binding (linear combination of atomic orbitals—LCAO form) used in Figs. 1 and  4, or values of the wave function functional (see the text) on the top surface (the latter can be used to simulate the STM image) utilized in Fig. 5. The linear combination of single-dopant representations then approximates the representation of the double-dopant system.

Figure 5 shows a decomposition of the double-dopant wave-function; however, using values of the STM-like wave function functional near the top 2D surface, which is relevant for the image construction, instead of the 3D wave function, as was done before. Effectively, this is a projection restricted to the 2D STM-image plane to determine the overlap relevant to the STM image. This difference is shown schematically in Fig. 6. We reiterate that, in Figs. 1 and  4, the dopant wave function has been projected in the basis of single dopant states. This projection captures the overlap everywhere. Here, in Fig. 5, we emphasize that a two-dimensional wave-function image (i.e. before applying absolute square in Eq. (1) from “Methods” Section) is decomposed into terms originating from the single dopant states capturing only the contribution from the image plane.

Comparing Figs. 4 and  5 shows that there is a broader spread in the contributions from the single-dopant ground states. This is especially noticeable for small dopant separation. The contribution can be almost as low as 50% even though the sum more completely exhausts the 2D projection. The presence of tip-orbitals with non-trivial (other than s) spatial dependence apparently further enhances the role of T$_2$ states and higher spectral components, reaching over 20% of the STM image weight in many cases. Again, this is especially true for small dopant separations, suggesting a contribution that limits the STM resolution.

STM image ambiguity

Figure 7

Example of an ambiguous multi-dopant configuration. The top row corresponds to dopants in their actual positions, $\left( 2,-1.5,-4.5\right)$ l.c., and $\left( -0.75,1.75,-4.25\right)$ l.c., while the bottom row references dopants in different positions, i.e. $\left( 0.5,0.5,-3\right)$ l.c. and $\left( 0.75,-0.25,-5.25\right)$l.c., for which the linear combination of wave functions gives a quantitatively better match to the multi-dopant STM image (on the right-hand side). The full TB picture for alternative dopant positions (not shown here) is very different from (c,g,d).

The above findings profoundly affect STM image simulation, as shown in Fig. 7. The top row on the left part of Fig. 7 demonstrates how a double-dopant image can be created from two (a and b) separate, single-dopant (ground – e1) wave functions to form a simulated image (c) that matches with very high (pixel-by-pixel 92.3%) accuracy (see the “Methods” section for the definition of the pixel-by-pixel comparator) the STM simulation done with a full tight-binding calculation for the double-dopant system and shown in (d). It must be emphasized here that (c) was not obtained by combining STM images (a, b) of individual dopants but by combining underlying wave functions of individual dopants to obtain the best possible fit to a full double-dopant simulation (Fig. 6). Thus, this allows for the onset of complicated interference patterns that occur in Si due to its multi-valley character.

The correct dopant positions can lead to a good match with the exact image. However, other choices for the dopant positions can give a better match. As shown in the bottom row of Fig. 7, one can find another erroneous, spatial combination of single-dopant positions (e,f) that will lead to an STM simulation (g) with even better pixel-by-pixel (94.4%) accuracy with respect to the double-dopant STM image (d). Importantly, the STM image from full TB calculations involving alternative positions bears no resemblance to (c), (d), or (g). Thus, combining single-dopant, ground-state wave functions into a double-dopant wave function may lead to ambiguity as it can produce an STM image that better matches the target picture despite the incorrect dopant positions. As shown by previous work^5,8, dopants occupying different spatial positions can have very different STM images. This can be seen by comparing (a), (b), (e) and (f). However, this sensitivity to lattice position is obscured in the double dopant STM images found using the ground-state wave functions of the two individual dopants.

Spatial metrology of double dopants

Figure 8

Efficiency of an inverse, position-finding approach as a function of cutoff distance for inter-dopant separation, e.g. ”5 l.c.” corresponds to all double-dopant pairs with five lattice-constants inter-dopant spacing or more. The plot has been obtained by a fitting involving dopant ground states (e1) only, as well as first excited (e2) and higher excited states using a scheme described in the text.

Determining double-dopant positions from their STM images is a formidable task. Even assuming that calculated pictures accurately match experimental positions⁸, the most straightforward approach, i.e., running calculations for all possible cases of dopants occupying, e.g. 10 nm $\times$ 10 nm $\times$ 5 nm box, would involve approximately 25 $\times 10^3$ atoms, and thus lead to a prohibitive number of over 6 $\times 10^8$ full tight-binding calculations. Recently, a solution utilizing machine learning has been proposed⁵ that reduces this complexity severely but still involves $10^5$ full calculations at the training stage (although this number can be reduced using spatial symmetries). Dramatic efficiencies can be achieved, in terms of many fewer TB calculations if the wave functions of the individual dopants can be used to simulate double-dopant STM images. Even greater efficiencies could be achieved for imaging multi(i.e., greater than 2)-dopants. As we have shown, significant issues arise if only the ground-state single-dopant wave functions are used to simulate double-dopant wave functions and images. We now show that significant improvement in simulating double-dopant STM images with single-dopant wave functions can be achieved by including contributions from single-dopant excited states.

To study the problem further and aim for a practical, computationally efficient way to determine the double-dopant position from their images, we use a fitting approach combining not only the single-dopant ground states (e1) but also higher (e2–e6) dopant states to obtain the best possible fit. Fig. 8 (e1) shows the efficiency of such fits measured as the success ratio that a fit for the correct positions also produces an STM image that best matches the double-dopant image. 665 randomly selected, shallowly placed, double dopant systems are studied. The dopant positions are randomly selected from a uniform distribution centered at the middle of the computational box to avoid boundary effects, with inter-dopant separations varying from 3 to 12 lattice constants, i.e., from 1.6 to 6.5 nm. A threshold is used in Fig. 8 to limit the separation of double-dopants, e.g., 5 corresponds to an inter-dopant distance equal to or larger than five lattice constants. As shown in Fig. 8, due to problems discussed earlier, fitting the STM image with single dopants (e1) states is successful for only 65% of all considered cases (including small and large inter-dopant separations), and at most 82% for the largest separation shown on the plot.

Based on Fig. 5, we propose a simple, brute-force scheme in which one first aims to find a solution with single-dopant ground states (e1) only. A full tight-binding calculation verifies the result to exclude the possibility of finding a spurious solution discussed earlier in Fig. 7. At this stage, more than 64% of dopant positions are correctly resolved, consistent with earlier discussions. If no match is found with e1 states, the rest of the cases (i.e., 35.6%) are processed/searched with another fit, that now includes both e1 and e2 states (we note that e2 is non-degenerate due to the presence of the reconstructed surface). Finally, a potential result is accepted (or rejected) by a second full tight-binding calculation.

Including the e2 state in the fitting process (at a price of a moderate increase in computational complexity), i.e., fitting a total 4 expansion coefficients, can be done straightforwardly because the nearby surface lifts the degeneracy of of the T$_2$ states. Adding the e2 state to the fitting leads to significantly increased efficiency reaching over 90% threshold for inter-dopants distances equal to 5 l.c. (2.7 nm) or more. It must be emphasized here that these fits are obtained without multiple tight-binding calculations performed for a double-dopant system but by combining only several dozen⁸ wave functions (pre-computed) from a single-dopant calculation. The time-consuming double-dopant tight-binding calculation is thus performed only twice, and for validation reasons only (accuracy check calculation after the fitting process).

Because this is important, let’s rephrase it: we start with a target STM image of a double dopant. Next, we do a fit using the two e1 states to generate possible STM images. We adjust the coefficient in the simulation to get the best fit of the simulated image to the target. We do this for multiple possible dopant positions to get the best of the best fits. This gives us a best guess for the dopant positions. Next, we check with a full TB calculation using the best guess dopant positions. If this exact calculation for the best positions matches the target (using a pixel-by-pixel comparator), we call it a success. If the best guess for positions does not match, then we add the e2 states and repeat. We can use test cases to guide the choice of a matching criteria for success.

Such a scheme, despite the large search space, is computationally effective since it avoids multiple time-consuming tight-binding computations for many double-dopant pairs and should provide >90% efficiency, with only two full double-dopant tight-binding calculations (as well as clear information on whether it succeeded or not) for experimentally relevant cases of double-dopants with spacings greater than 2.7 nm. Although the inclusion of higher dopant states (e3, e4, e5, and e6) can somewhat improve the accuracy (especially for closely-spaced systems), we found it comes with prohibitive computational complexity (especially when e5 and e6 are included).

The presented algorithm can be further optimized: even with the simple fit using only e1, most mismatched cases are expected to lie close to the correct positions. In fact, a significant fraction of incorrectly assigned test cases happened when only one of the dopants was misassigned (see Supporting information). This happens, on average, in over 1/2 of all missed cases and in about 80% of the cases when the dopants are separated by more than 5 l.c. When we know that one dopant has been misassigned, our algorithm can utilize this information by performing secondary (including both e1 and e2) fits starting in the vicinity of the dopant wrongfully assigned in the simple fit, thus considerably speeding up a search. Our scheme is also much simpler than an alternative machine (deep) learning approach involving complicated neural networks⁵ and resource greedy learning process, although at a price of somewhat smaller efficiency.

We also note that the range of distances studied in Fig. 8 forms the biggest challenge. For even larger distances and (effectively) decoupled dopants, the theoretical accuracy starts to approach 100%, yet with all the limitations and pitfalls occurring for single dopants.⁸

For the smallest distance ($\le$2 l.c.) inter-dopant spacings, where the quasi-molecular wave functions are the most complicated, the search space is reduced and is relatively small. It is also further reduced substantially by taking into account underlying (reconstructed) lattice symmetries⁵ and at most $10^4$ full TB calculations should be performed to build a simple library of images of closely spaced dopants that could be directly compared with experiment to resolve dopant positions. Although large, such a number is still smaller than the number of learning cases ($10^5$) necessary at the stage of neural network learning, which must handle both large and small inter-dopant separation. Such a library approach for closely spaced dopants could work provided problems with spatial metrology of single dopants⁸ are resolved, that is, matching theory with experiment, and provided factors like noise, etc., can be effectively handled.

To conclude, if an inverse approach is used to determine the positions of dopant atoms forming a double dopant, and such an approach is based on utilizing single-dopant ground-state wave functions, erroneous results can occur. This problem stems from the complicated, multi-orbital character of the double-dopant wave function. The accuracy of the solution can be increased significantly by adding e2 states to the modeling at a moderate computational cost.

Discussion

To summarize, we performed a large series of STM simulations for double phosphorous dopants in silicon using a state-of-the-art, empirical tight-binding approach with d-orbitals. Our model achieves high-quality STM simulations for single dopants, in excellent agreement with recent theoretical and experimental works. Here, we used this theory to study a statistically meaningful ensemble of 1689 double dopants placed at different sites of a host Si lattice. We aimed to understand how the double-dopant ground state, the quasi-molecular wave function, can be re-expressed in terms of single-dopant wave functions. As a result, already for the buried dopant (deep below the Si surface), we found that the double-dopant wave function has components originating from excited dopant T and E$_2$ states. This result immediately suggests that modeling a multi-dopant system² using a theory neglecting the presence of higher dopant states may be inaccurate for some cases.

This effect is even more pronounced for shallow-buried, double dopants that are affected by the presence of reconstructed and passivated silicon surfaces. In this case, the double-dopant wave function has up to 20% contribution from single-dopant excited states. The surface modifies not only the individual dopant wave functions but also the expansion coefficients of the quasi-molecular ground state calculated in the basis of single-dopant states. The simplest approach, which uses single-dopant ground states to simulate the STM image of a double-dopant, can fail routinely. It is possible to find incorrect solutions corresponding to erroneous positions of two dopants that match the double-dopant STM image better than the image obtained for the correct placement of two dopants. However, the image simulation can be improved, especially for distantly spaced dopants, by including the first excited (e2) dopants states in modeling, resulting in over 90% success rate for dopants separated from each other by more than 5 l.c. (2.7 nm) and in a success rate of more than 80% for all dopant separations studied. Most of the improvements in simulating STM images and extracting dopant positions can be achieved by including only the e1 and e2 single-dopant states. The computationally expensive inclusion of higher states (e3-e6) into the fitting, especially for closely spaced dopants, does not allow for reaching the 90% accuracy threshold.

Double-dopant wave functions have complicated multi-orbital character, which stems from mixing between ground and excited single-dopant states occupying the different sites of the double dopant. This is important for simulating STM images and accurately extracting dopant positions for double-dopant pairs. In other contexts, this further indicates the importance of carefully modeling inter-orbital hopping integrals, consistent with our recent work¹² and using such results to build accurate Fermi-Hubbard models for carrying out analog quantum simulation on dopant arrays.

Methods

Tight-binding calculations

The ground state of single and double dopants is obtained with the nearest neighbor, empirical tight-binding method accounting for d-orbitals^14,15,16,17 with reconstructed surface-atom positions¹⁸, and with explicit surface passivation that accounts for the presence of hydrogen atoms¹⁹. Here, for Si we use the sp$^3$d$^5$s* parametrization of Boykin et al.²⁰, accounting for multi-band and multi-valley couplings. The details of the sp$^3$d$^5$s* tight-binding calculations were discussed thoroughly in our earlier papers^{15,16,21,22,23}.

The computational domain is a cubic box of 30 lattice constants (approximately 16.2 nm) in each spatial direction, which is large enough for the STM simulations to converge. It uses a relatively small (0.22 million) number of atoms in the computational box. Since we found that the STM image simulation does not depend on spin-orbit interaction, we neglect the spin-orbit mixing term in the Hamiltonian, allowing us to work with a real Hamiltonian matrix with significant benefits in terms of computational efficiency and time. Thousands of separate atomistic simulations were performed on a 128 CPU-core system using Jacobi-Davidson solver as implemented in the SLEPc/PETSc library.

Each phosphorous dopant is represented by a dynamically-screened electrostatic potential $(\varepsilon (r)\,r)^{-1}$ with central-cell correction values tuned so the energy levels of the lowest six dopant bound states match the respective experimental values. We have used the dynamic dielectric screening^4,24,25 model of Ref.²⁵ with $\epsilon _{\infty } = 11.4 \epsilon _0$, with central-cell correction equal to $-3.755$ eV, reproducing the binding energy ($-45.585$ meV), in excellent agreement with the experimental value of $-45.58$ meV²⁶. We have also incorporated separate central-cell shifts of p and d orbital energies ($\Delta E_\text {p} =1.195$ eV, and $\Delta E_\text {d}=1.211$ eV respectively) to reproduce better the energies of excited dopant levels, again with excellent (within several µeV) agreements with experimental values (T$_2=-33.9$ meV, E$=-32.6$ meV). Additionally, we accounted for strain introduced by incorporating phosphorus into the silicon lattice, which causes the extension of the Si-P bond by 1.7%. The effect of strain was incorporated in the Hamiltonian by re-scaling the Si-P hopping matrix elements using Harrison’s law. We note, however, that neither the screening model nor the inclusion of strain has any visually discernible effect on resulting STM images. Although this leads to a different conclusion as compared to Ref.²⁷, this should not come as a surprise since a static screening model with $\epsilon _{\infty } = 11.4 \epsilon _0$ and without strain (with central cell correction of $-3.689$ eV, and $\Delta E_\text {p}=1.146$ eV $\Delta E_\text {d}=1.099$ eV) also provides excellent agreement with experimental dopant levels energies. We emphasize that in any (static or non-static) screening model, the actual choice of $\epsilon _{\infty }$ seems to play a crucial role. Moreover, contrary to a model studied in Ref.²⁸, our static screening model already provides a good value of a squared magnitude of the ground state wave function at the donor nuclear site $\left| \psi \left( r_0\right) \right| ^2$ equal to $0.495 \times 10^{30}\,\text {m}^{-3}$, as compared to $0.43 \times 10^{30}\,\text {m}^{-3}$ given in the experiment²⁹. Including dynamic screening and strain provides a result even closer to the experiment and equal to $0.466 \times 10^{30}\,\text {m}^{-3}$. Finally, we note that allowing for a separate central-cell shift of s* orbitals (with a central cell correction of $-4.418$ eV, $\Delta E_\text {p} = 1.858$ eV, $\Delta E_\text {d} = 1.874$ eV, and $\Delta E_{\text {s}*} = 1.839$ eV) allowed us to reproduce the experimental result exactly, emphasizing the need for future studies to tight-binding dopant models. However, this work does not focus on modeling hyperfine properties. For consistency with our previous work (Ref.⁸), we use the dynamic screening model with strain but without s* optimization throughout this paper.

2D STM image simulation

For STM image simulation (as shown in Fig. 7), we have augmented the tight-binding basis^4,23 with Slater-type orbitals (STO) to model the atomic orbitals³⁰. We modify the s* orbital exponent, resulting in excellent agreement with experimental images from Ref.⁴. Finally, we note that an STM image is simulated by summing up contributions from the STOs associated with atoms on the silicon surface and below, with a cut-off radius of 2 nm.

A single tip orbital cannot capture all features in the experimental STM image^4,8. The STM image value $I(\textbf{r})$ from a general tip orbital and the dopant-state wave function in the imaging plane $\psi (\textbf{r})$ with contributions from s, p$_z$ and d$_{z^2-\frac{1}{3}r^2}$ tip orbitals, according to Chen’s approach¹³, is directly proportional to

$$\begin{aligned} I \propto \left| c_s \psi + \frac{c_p}{\kappa } \frac{\partial \psi }{\partial z} + \frac{c_d}{\kappa ^2} \left( \frac{2}{3} \frac{\partial ^2 \psi }{\partial z^2} - \frac{1}{3} \frac{\partial ^2 \psi }{\partial x^2} - \frac{1}{3} \frac{\partial ^2 \psi }{\partial y^2} \right) \right| ^2 \end{aligned}$$

(1)

where contributions from s, p$_z$ and d$_{z^2-\frac{1}{3}r^2}$ orbitals, are defined as $c_\text {s}^2$, $c_\text {p}^2$ and $c_\text {d}^2$, respectively, with $c_\text {s}^2 + c_\text {p}^2 + c_\text {d}^2 = 1$ and z is the vertical direction perpendicular to the surface. Parameter $\kappa$ quantifying the vacuum decay of the Slater orbitals is assumed to have a constant value of 1.3 Å$^{-1}$ = 0.013 pm$^{-1}$, in agreement with the methodology presented in Ref.⁴, and our earlier work⁸.

2D charge density simulation

Based on the wave function in LCAO form, i.e. $c_{i\alpha }$ (where i is the index of an atom and $\alpha$ is the index of the orbital in sp$^3$d$^5$s* basis set) it is possible to calculate the charge corresponding to each atom as $\sum _\alpha c_{i\alpha }^2$. For strain-free systems analyzed in this paper (apart from the surface reconstruction effects), one can superimpose a regular three-dimensional grid on the diamond cubic lattice of silicon atoms¹¹. By combining the charge corresponding to the grid points along the z axis, this approach allows to calculate a two-dimensional charge density map without using any auxiliary orbital set, as shown in Figs. 2 and  3.

Wave function representation

Each single- or multi-dopant eigenstate can be associated with a representation. In our analysis, we will use two different representations.

• 1. Tight-binding coefficients of given eigenstate. This way (used in Figs. 1, 2, 3, 4), each eigenstate is represented as a vector of coefficients of size equal to the number of orbitals per atom × the number of atoms. The scalar product is defined as with regular vectors.

• 2. Functional of the wave function on a given surface. This way (used in Figs. 5 and 7), for each eigenstate, we calculate the values of the wave function and its derivatives on a regular grid on a given surface perpendicular to the z direction. The resulting representation consists of the values of the specific functional corresponding to the STM tip of mixed s, p$_z$, and d orbitals (squared coefficients of 14.6%, 72.5%, and 12.9%, respectively), according to Chen’s approach¹³. As a result, the STM image can be obtained by taking the squares of the representation values. The scalar product is defined as pixel-by-pixel multiplication and summation over the entire surface.

Both representations allow us to model eigenstates’ charge densities on two-dimensional surfaces. In representation 1, as described in section 2D charge density simulation above, atoms of the strain-free system can be overlaid on a regular, three-dimensional grid¹¹ and the charge (sum of squared TB coefficients corresponding to each atom) summed in a direction perpendicular to a surface on which we need to visualize the charge distribution (bottom rows of Figs. 2 and 3). In the second representation, as described in section 2D STM image simulation, the charge is calculated as squared values of STM-like functional associated with Slater orbitals. The latter variant can be visualized on a grid of arbitrary resolution (as in Fig. 7).

Given two 2D images I(x, y) and J(x, y) corresponding to the same representation and $L^2$-normalized ($\sum _{(x,y)} I(x,y)^2 = \sum _{(x,y)} J(x,y)^2 = 1$), the accuracy, or difference between two images can be calculated using a pixel-by-pixel least squares comparator i.e. $\sum _{(x, y)} \left( I(x,y) - J(x,y) \right) ^2$.

Contribution analysis of two-dopant systems

Regardless of the representation chosen, one can compare the ground state of the two-dopant system with the eigenstates of two systems consisting of individual dopants. The problem is, since the latter comes from two separate diagonalizations (one for each dopant position), these are not pairwise orthogonal. As a result, coefficients calculated as scalar products between the two-dopant ground state and single-dopant eigenstate, squared, would not add up to one and, therefore, would not be suitable for a contribution analysis.

Therefore, an orthogonalization scheme must be used and with this in mind, the double-dopant representation $\Psi _0$ can be approximated as a linear combination of n representations of each dopant

$$\begin{aligned} \Psi _0 \approx \Psi = \sum _{i=1}^n {\langle {\varphi _i'|\Psi _0}\rangle } \varphi _i' + \sum _{i=1}^n {\langle {\psi _i'|\Psi _0}\rangle } \psi _i' \end{aligned}$$

(2)

where $\varphi '$ and $\psi '$ are Gram-Schmidt orthogonalized representations corresponding to consecutive eigenstates of the first and second dopant, respectively:

$$\begin{aligned} \begin{aligned} \varphi _1'&= \varphi _1 \\ \psi _1'&= \psi _1 - {\langle {\varphi _1'|\psi _1}\rangle } \varphi _1' \\ \varphi _n'&= \varphi _n - \sum _{i=1}^{n-1} {\langle {\varphi _i'|\varphi _n}\rangle } \varphi _i' - \sum _{i=1}^{n-1} {\langle {\psi _i'|\varphi _n}\rangle } \psi _i' \\ \psi _n'&= \psi _n - \sum _{i=1}^{n} {\langle {\varphi _i'|\psi _n}\rangle } \varphi _i' - \sum _{i=1}^{n-1} {\langle {\psi _i'|\psi _n}\rangle } \psi _i', \end{aligned}\end{aligned}$$

(3)

where $\varphi '_n$ and $\psi '_n$ are re-normalized after the n-th step.

The similarity between $\Psi _0$ and $\Psi$ is then calculated as ${\langle {\Psi _0|\Psi }\rangle } = \sum _{i=1}^n {\langle {\Psi _0|\varphi _i'}\rangle }^2 + \sum _{i=1}^n {\langle {\Psi _0|\psi _i'}\rangle }^2$, giving quantitative contributions of $\psi _i'$ in the two-dopant ground state $\Psi _0$. In the same way, one can calculate the similarity between $\Psi _0$ and any given pair of n-th states $\varphi _n$ and $\psi _n$. The results are the same as would be obtained with any equivalent method, e.g., based on inverting the covariance matrix formed between all eigenstates. Moreover, the apparent asymmetry between $\varphi$ and $\psi$ in Eq. (3) does not affect the results, as we always account for both dopants for each n.

The resulting contributions are shown for many different spatial dopants configurations in Figs. 1 and  4 (representation 1) as well as in Fig. 5 (representation 2).