Introduction

Numerical simulations of cardiac cells have traditionally followed two primary approaches: membrane models, which are expressed as systems of ordinary differential equations1,2, or spatial models, such as the bidomain model (BD) and monodomain model (MD)3,4. Membrane models, due to their lack of spatial variation, are unable to explain important spatial phenomena like reentry, arrhythmias, or fibrillation. These spatial aspects have been extensively investigated using the BD and MD models. However, the BD and MD models are based on homogenization or averaging approaches3,5,6,7, leading to the removal of the cardiomyocyte from the simulations. While this simplifies the models, it also significantly restricts their resolution. As a result, BD and MD are not well-suited for modeling electrophysiological processes at the level of individual cells, which is a critical limitation in understanding cardiac dynamics and the origin of arrhythmias.

With the continuous increase in computing power and advancements in numerical solution techniques for partial differential equations, the potential for enhancing the resolution of cardiac tissue models has become evident. This advancement has been a key focus of the MICROCARD project8, which aims to provide simulation software capable of sub-cellular resolution. Such software is pivotal for analyzing the progression from cellular and sub-cellular level perturbations to the initiation of cardiac arrhythmias.

In the traditional BD and MD models, the extracellular space (E), the cell membrane (M), and the intracellular space (I) are uniformly distributed throughout the computational domain. However, more accurate cell-based models distinctly separate these domains. Consequently, these models are now often referred to as EMI models, but they were earlier referred to as microscopic models9. The development of EMI models is presented in Refs.10,11,12,13,14,15,16, and their applications are explored in Refs.17,18,19,20,21,22. Numerical methods for solving the EMI equations have been analyzed in Refs.23,24,25,26,27. Additionally, the properties and efficiencies of these solvers have been evaluated in Refs.7,23,28,29,30,31,32, and special methods for mesh generation for EMI models have been addressed in Ref. 33.

The use of EMI models is associated with a considerable increase in computational demands. The extent of the increase depends on the actual application under consideration, but from the definition of the models it is quite clear that whereas the BD and MD models provide average solutions over many cardiomyocytes, the EMI models resolve every cell into a large number of mesh blocks13. For specific applications, it may very well occur that BD and MD are too coarse but the EMI models are more accurate than what is actually required. This has motivated the development of models of intermediate resolution aiming at balancing computational cost and physiological resolution. These models are cell-based and referred to as the Kirchhoff network model (KNM34), and as the associated simplified Kirchhoff network model (SKNM35). KNM and SKNM are based on representing individual cells and are similar to previous models of small collections of cardiomyocytes36,37.

The aim of this paper is to evaluate the computational demands and physiological accuracy of the five models, EMI, BD, MD, KNM, and SKNM. Initially, we determine the mesh resolutions required for numerically accurate solutions. These resolutions form the basis for assessing the computational needs of each model. Subsequently, we analyze how these models simulate the electrochemical wave in the vicinity of an infarcted area. Specifically, we consider a scar core surrounded by a border zone which again is surrounded by healthy tissue. Border zone and scar tissue are known to be sources of arrhythmias as illustrated in several computational studies; see, e.g., Refs.38,39. The considered models exhibit marked variations in conduction velocity as the excitation wave traverses the border zone between healthy and infarcted tissue. Such variations are critical, as they may lead to divergent interpretations about the presence of reentry waves, which in turn could be the precursors of life-threatening arrhythmias. Additionally, we present a case where the sub-cellular resolution of the EMI model is essential to demonstrate how a non-uniform distribution of certain ion channels along the cell membrane can significantly alter membrane dynamics.

Methods

In this section, we briefly present the models, EMI, BD, MD, KNM and SKNM. We start with the EMI model, which is the most detailed model, and base the presentation of the other models on the EMI model formulation.

The extracellular-membrane-intracellular model (EMI)

In the EMI model, the spatial domain consists of a number of cells, \(\Omega _i^k\), and a surrounding extracellular space, \(\Omega _e\) (see Fig. 1a). The interface between \(\Omega _i^k\) and \(\Omega _e\) defines the cell membrane, \(\Gamma _k\). In addition, the interface between two neighboring cells, \(\Gamma _i^k\) and \(\Gamma _i^j\), defines an intercalated disc, \(\Gamma _{k,j}\). The EMI model for the electrical potential in and surrounding the excitable cells can be expressed by the following system of equations (see, e.g., Refs.10,12),

$$\begin{aligned} \nabla \cdot \sigma _i\nabla u_i^k&= 0&\text {in } \Omega _i^k, \end{aligned}$$
(1)
$$\begin{aligned} \nabla \cdot \sigma _e\nabla u_e&= 0&\text {in } \Omega _e, \end{aligned}$$
(2)
$$\begin{aligned} C_m\frac{\partial v^k}{\partial t}+ I_{\textrm{ion}}^k(v^k, s^k)&= n_e\cdot \sigma _e\nabla u_e = -n_i^k\cdot \sigma _i\nabla u_i^k&\text {at } \Gamma _k, \end{aligned}$$
(3)
$$\begin{aligned} v^k&= u_i^k - u_e&\text {at } \Gamma _k, \end{aligned}$$
(4)
$$\begin{aligned} \frac{\partial s^k}{\partial t}&= F_k(s^k, v^k)&\text {at } \Gamma _k, \end{aligned}$$
(5)
$$\begin{aligned} C_g\frac{\partial w^k}{\partial t}+I_{\textrm{gap}}^{k,j}(w^k)&= n_i^{j}\cdot \sigma _i\nabla u_i^{j} = -n_i^k\cdot \sigma _i\nabla u_i^k&\text {at } \Gamma _{k, j}, \end{aligned}$$
(6)
$$\begin{aligned} w^k&= u_i^k - u_i^j&\text {at } \Gamma _{k, j}, \end{aligned}$$
(7)

for each cell k with neighbors j. Here, \(n_i\) and \(n_e\) are the outward pointing normal vectors of the intracellular domain and the extracellular domain, respectively. The unknown variables of the model are the intracellular potentials in each cell, \(u_i^k\) (in mV), defined in \(\Omega _i^k\), the extracellular potential surrounding the cells, \(u_e\) (in mV), defined in \(\Omega _e\), the membrane potential of each cell, \(v^k\) (in mV), defined at the membrane, \(\Gamma _k\), and the intercalated disc potentials, \(w^k\), defined at the intercalated discs, \(\Gamma _{k,j}\).

Figure 1
figure 1

Illustration of the components of the computational mesh for the EMI model. (a) Illustration of an EMI model mesh for 2 × 2 connected cells. The orange volumes are the cells, \(\Omega _i^k\), and the pink volume is the extracellular space, \(\Omega _e\). The cell membrane, \(\Gamma _k\), is defined at the boundary surface between the intracellular and extracellular spaces, and the intercalated discs, \(\Gamma _{k,j}\), are defined at the boundary surface between two cell volumes, \(\Omega _i^k\) and \(\Omega _i^j\). Note that the extracellular space surrounds the cells on all sides, but the upper half of the extracellular volume is removed from the illustration to make the cells visible. (b) Illustration of the geometry of the cells. The cells are shaped as cylinders with length \(l_x\) = 100 μm and diameter ranging between 16 μm at the cell ends and 21 μm at the center of the cells. (c) Illustration of one computational element in the EMI model mesh. Each element is made up of four computational nodes with a typical distance of \(\Delta x\).

Full size image

In addition, a number of additional state variables, \(s^k\), are defined at the membrane, representing ionic concentrations and gating variables for the ion channels used to compute the ionic membrane current density, \(I_{\textrm{ion}}^k\) (in μA/cm\(^2\)). The dynamics of these state variables are modeled by \(F_k\). We use the adult ventricular membrane model from Ref. 40 for \(F_k\) and \(I_{\textrm{ion}}^k\). The formulation of this model is found in the Supplementary Information.

The parameters of the EMI model are the intracellular conductivity, \(\sigma _i\) (in mS/cm), the extracellular conductivity, \(\sigma _e\) (in mS/cm), the specific membrane capacitance, \(C_m\) (in μF/cm\(^2\)), and the specific intercalated disc capacitance, \(C_g\) (in μF/cm\(^2\)). Furthermore, the current density between neighboring cells, \(I_{\textrm{gap}}^{k,j}\), is modeled by a simple passive model

$$\begin{aligned} I_{\textrm{gap}}^{k,j}&= \frac{1}{R_g^{j,k}}w^k&\text {at } \Gamma _{k,j}, \end{aligned}$$
(8)

where \(R_g^{j,k}\) (in k\(\Omega\)cm\(^2\)) is the resistance of the gap junctions connecting cells k and j.

The default parameter values used in our simulations are provided in Table 1. The cells are shaped as cylinders with length \(l_x\) = 100 μm and radius ranging between 8 μm at the cell ends and 10.5 μm at the center of the cells (see Fig. 1b). The distance between cell centers in the y-direction is \(l_y\) = 20 μm. The minimum distance between the intracellular space to the outer boundary of the extracellular space is 5 μm.

Table 1 Default parameter values used in the EMI model simulations.
Full size table

The bidomain model (BD)

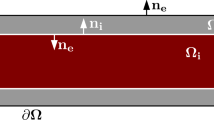
In the bidomain model (BD), the tissue is not separated into distinct intracellular and extracellular parts as in the EMI model. Instead, both the intracellular space, the membrane and the extracellular space are assumed to exist everywhere in the domain (see Fig. 2a). Based on this assumption, a formulation of BD can be derived from the EMI model7. The bidomain model reads

$$\begin{aligned} C_m\frac{\partial v}{\partial t}&= \chi ^{-1}\left( \nabla \cdot \left( M_i\nabla v\right) + \nabla \cdot \left( M_i\nabla u_e\right) \right) - I_{\textrm{ion}}(s,v), \end{aligned}$$
(9)
$$\begin{aligned} 0&= \nabla \cdot \left( M_i\nabla v\right) + \nabla \cdot \left( (M_i + M_e)\nabla u_e\right) , \end{aligned}$$
(10)
$$\begin{aligned} \frac{ds}{dt}&= F(s,v), \end{aligned}$$
(11)

where v (in mV) is the membrane potential, and \(u_e\) (in mV) is the extracellular potential. In addition, \(I_{\textrm{ion}}\), s and F are the ionic current density, additional state variables and the dynamics of the additional state variables, modeled by the membrane model from Ref. 40 like for the EMI model. The BD parameters can be defined based on the EMI model mesh and parameters7. In particular, \(\chi\) is the membrane surface to volume ratio, which can be computed by

$$\begin{aligned} \chi = \frac{\sum _k\int _{\Gamma _k} 1\,dS}{\int _{\Omega _e} 1\,dV + \sum _k\int _{\Omega _i^k} 1\,dV}, \end{aligned}$$
(12)

from the EMI model mesh. Furthermore, for a two-dimensional collection of cells

$$\begin{aligned} M_i&= \begin{pmatrix}M_i^x &{} 0\\ 0 &{} M_i^y\end{pmatrix},&M_e&= \begin{pmatrix}M_e^x &{} 0 \\ 0 &{} M_e^y\end{pmatrix}, \end{aligned}$$
(13)

where

$$\begin{aligned} M_i^x&= \frac{\delta _i \sigma _i}{1+\delta _i\sigma _i\frac{l_yL_zR_g}{l_x}}, \end{aligned}$$
(14)
$$\begin{aligned} M_i^y&= \frac{\delta _i \sigma _i}{1+\delta _i\sigma _i\frac{l_xL_zR_g}{l_y}}, \end{aligned}$$
(15)
$$\begin{aligned} M_e^x&= M_e^y = \delta _e\sigma _e, \end{aligned}$$
(16)

and \(l_x\) is the cell length, \(l_y\) is the cell width, \(L_z\) is the width of the domain in the z-direction, and \(\delta _i\) and \(\delta _e\) are the intracellular and extracellular volume fractions, respectively. These volume fractions can be computed from the EMI model mesh by

$$\begin{aligned} \delta _i&= \frac{\sum _k\int _{\Omega _i^k} 1\,dV}{\int _{\Omega _e} 1\,dV + \sum _k\int _{\Omega _i^k} 1\,dV}, \end{aligned}$$
(17)
$$\begin{aligned} \delta _e&= 1-\delta _i. \end{aligned}$$
(18)

For a one-dimensional collection of cells, we have

$$\begin{aligned} M_i&= M_i^x&M_e&= M_e^x, \end{aligned}$$
(19)

where \(M_i^x\) and \(M_e^x\) are given by (14) and (16) with the cell width \(l_y\) replaced by the domain width \(L_y\), which is equal to the cell width plus the width of the extracellular space (30 μm in our 1D simulations).

The monodomain model (MD)

The monodomain model (MD) can be derived from the BD model based on the assumption

$$\begin{aligned} M_e=\lambda M_i. \end{aligned}$$
(20)

The model then reads

$$\begin{aligned} C_m\frac{\partial v}{\partial t}&= \frac{\lambda }{\chi (1+\lambda )} \nabla \cdot \left( M_i\nabla v\right) - I_{\textrm{ion}}(s,v), \end{aligned}$$
(21)
$$\begin{aligned} \frac{ds}{dt}&= F(s,v). \end{aligned}$$
(22)

In the 1D simulations reported in the “Results” section, the condition (20) holds, and we define,

$$\begin{aligned} \lambda = \frac{M_e}{M_i}. \end{aligned}$$
(23)

For the reported 2D simulations, where (20) does not hold, we apply the approximation of \(\lambda\) from Ref. 35

$$\begin{aligned} \lambda&= \frac{\int _{\Omega }M_e^xM_i^x\,dS + \int _{\Omega }M_e^yM_i^y\,dS}{\int _{\Omega }(M_i^x)^2\,dS + \int _{\Omega }(M_i^y)^2\,dS}, \end{aligned}$$
(24)

where \(\Omega\) is the computational domain and \(M_i^x\), \(M_i^y\), \(M_e^x\), and \(M_e^y\) are defined in (14)–(16).

The Kirchhoff network model (KNM)

In the Kirchhoff network model (KNM), each cell in the excitable tissue is represented by a single nodal point, as opposed to being spatially resolved as in the EMI model (see Fig. 2a). In addition, the extracellular space surrounding each cell is represented in each node. The model is derived by applying Kirchhoff’s current law for each nodal point34 and reads

$$\begin{aligned} C_m\frac{dv^k}{dt}&= \frac{1}{A_m^k}\sum _{j\in N_k}\{G_i^{j,k} (v^{j} - v^{k})+ G_i^{j,k} (u_e^{j}-u_e^{k})\} - I_{\textrm{ion}}^k(v^k, s^k), \end{aligned}$$
(25)
$$\begin{aligned} 0&= \sum _{j\in N_k}G_i^{j,k}\left( v^{j} -v^{k} \right) + \sum _{j\in N_k}(G_i^{j,k}+G_e^{j,k})(u_e^{j}-u_e^{k}), \end{aligned}$$
(26)
$$\begin{aligned} \frac{ds^k}{dt}&= F_k(s^k,v^k). \end{aligned}$$
(27)

for all k numbering the cells in the tissue. Here, \(v^k\) is the membrane potential of cell k (in mV), \(u_e^k\) is the associated extracellular potential (in mV), and \(N_k\) is a collection of all the neighboring cells of cell k. Furthermore, \(I_{\textrm{ion}}^k\), \(s^k\) and \(F_k\) are the ionic current density, additional state variables and the dynamics of the additional state variables, modeled by the membrane model from Ref. 40 like for the EMI model. Moreover, \(A_m^k\) (in cm\(^2\)) is the membrane area of cell k, and can be computed from the EMI model mesh by

$$\begin{aligned} A_m^k = \int _{\Gamma _k} 1\;dS. \end{aligned}$$
(28)

The parameters \(G_e^{j,k}\) and \(G_i^{j,k}\) are conductances defined by,

$$\begin{aligned} G_e^{j,k}&= \delta _e^{j,k}\frac{A_{j,k}\sigma _e}{l_{j,k}}, \end{aligned}$$
(29)
$$\begin{aligned} G_i^{j,k}&= \frac{1}{\frac{l_{j,k}}{\delta _i^{j,k}A_{j,k}\sigma _i} + R_g^{j,k}}, \end{aligned}$$
(30)

where \(\delta _i^{j,k}\) and \(\delta _e^{j,k} = 1- \delta _i^{j,k}\) are the extracellular and intracellular volume fractions, respectively, associated with cell k. These are assumed to be constant throughout the domain and defined by (17) and (18). In addition, \(A_{j,k}\) is the cross-sectional area (both intracellular and extracellular) between the centers of cell k and j and \(l_{j,k}\) is the distance between the centers. If the cells are connected in the x-direction, then \(A_{j,k} = l_yL_z\) (or \(A_{j,k} = L_yL_z\) in the 1D case) and \(l_{j,k} = l_x\). Similarly, if the cells are connected in the y-direction, then \(A_{j,k} = l_xL_z\) and \(l_{j,k} = l_y\).

The Simplified Kirchhoff network model (SKNM)

The Simplified Kirchhoff network model (SKNM) can be derived from KNM based on an assumption similar to that used to define MD from BD35. More specifically, based on the assumption

$$\begin{aligned} G_e^{j,k} = \lambda G_i^{j,k}, \end{aligned}$$
(31)

KNM simplifies to

$$\begin{aligned} C_m\frac{dv^k}{dt}&= \frac{\lambda }{A^k_m(1+\lambda )}\sum _{j\in N_k}G_i^{j,k} (v^{j} - v^{k}) - I_{\textrm{ion}}^k(v^k, s^k), \end{aligned}$$
(32)
$$\begin{aligned} \frac{ds^k}{dt}&= F_k(s^k,v^k). \end{aligned}$$
(33)

In our 1D strand simulations where (31) holds, we use the definition

$$\begin{aligned} \lambda = \frac{G_e^{j,k}}{G_i^{j,k}}. \end{aligned}$$
(34)

In the 2D simulations where the assumption (31) do not hold, we use the approximation of \(\lambda\) from Ref. 35, i.e.,

$$\begin{aligned} \lambda = \frac{ \sum _{j,k}G_e^{j,k}G_i^{j,k} \frac{l^2_{j,k}}{A^2_{j,k}} }{ \sum _{j,k} (G_i^{j,k})^2 \frac{l^2_{j,k}}{A^2_{j,k}} }. \end{aligned}$$
(35)

Numerical implementation

The numerical implementation of each of the five models is described in the Supplementary Information. For the simulations in Figs. 2, 3, 4, 5, 6, 7, 8, 9, we use a Dell Precision 3640 Tower with an Intel Core processor (i9-10900K, 3.7 GHz/5.4 GHz) with ten cores with two threads each, but we only parallelize the computation of the membrane model part of the simulations (all models) and the intracellular parts (for EMI), see the Supplementary Information for more details. In addition, we consider a possible path for speeding up of the EMI model code. To investigate the parallel performance of this code, we use a 24-core AMD Epyc 7413 CPU, where up to 24 threads are used. The results of these speedup simulations are found in the Supplementary Information.

Conduction velocity, time of arrival and action potential duration

In addition to comparing the computational requirements associated with each of the five models described above, we also compare properties of the model solutions. More specifically, we consider three biomarkers of physiological relevance as well as the potential reentrant activity around an infarction scar. The first considered biomarker is the conduction velocity (CV), which is the velocity with which an electrical excitation wave travels between two points in the tissue. The second considered biomarker is the time of arrival (ToA), which is defined as the point in time when the excitation wave arrives at a single spatial point. This biomarker is closely related to the CV, as a fast CV typically results in an early ToA, whereas a slow CV typically results in a late ToA. The ToA can be useful for characterization of wave velocity in cases with a heterogeneous CV (as in our simulations of an infarction scar). The third considered biomarker is the duration of the action potential in a single spatial point, i.e., the action potential duration (APD). The precise definitions used to compute the biomarkers in our computations are provided in the Supplementary Information.

Results

Convergence of model solutions

Figure 2
figure 2

Model overview and convergence analysis. (a) Overview of the five considered models of cardiac conduction: EMI, KNM, SKNM, BD, and MD. In EMI, the extracellular space, the membrane and the cells are spatially resolved in 3D. In KNM, each cell and associated extracellular space are represented as single node points, and in SKNM, the representation is simplified to only represent each cell. In BD, the tissue is treated as a continuum consisting of both extracellular space, intracellular space and membrane everywhere. In MD, the BD representation is simplified to only represent the cell membrane. (b) Convergence analysis for the five models. We compute the conduction velocity (CV) along a strand of 30 cells for each model for a number of different spatial (\(\Delta x\)) and temporal (\(\Delta t\)) resolutions and report the difference (in percent) from the CV computed using the finest considered resolution (\(\Delta t = 1\;\upmu\)s, \(\Delta x = 3\;\upmu\)m). We consider three different values of the gap junction resistance, the default value, \(1\times R_g\), and \(50\times R_g\) and \(200\times R_g\). Note that there is no spatial resolution parameter for KNM and SKNM since the position of the cells define the node points. Furthermore, the operator splitting algorithm23 used to solve the EMI model is unstable for the default value of \(R_g\) (\(1\times R_g\)) and \(\Delta t \ge 50\;\upmu\)s. When adjusting one of the discretization parameters, the other is fixed at the finest resolution. (c) Conduction velocity computed using the finest resolution of each model for three different values of the gap junction resistance, \(R_g\).

Full size image

In Fig. 2b, we investigate the spatial and temporal resolutions required to obtain converged numerical solutions for the five models EMI, KNM, SKNM, BD, and MD. For each considered resolution and model, we compute the conduction velocity (CV), compare it to the CV computed for the considered model using the finest resolution (\(\Delta t = 1\;\upmu\)s, \(\Delta x = 3\;\upmu\)m), and report the difference in percent. Since we will use the models to study an example of an infarction scar with a border zone of reduced gap junction coupling (increased \(R_g\)), we investigate convergence both for the default gap junction resistance, \(1\times R_g\), and for two cases of increased resistance, \(50\times R_g\) and \(200\times R_g\), similar to what was done in Ref. 34. The gap junction resistance, \(R_g\), appears directly in Eq. (8) for the EMI model, in the definition of the intracellular conductivity tensor, \(M_i\), for BD and MD (see (14)–(15)), and in the definition of the intracellular conductance, \(G_i\), for KNM and SKNM (see (30)).

Temporal resolution

In the left panel of Fig. 2b, we investigate the effect of the time step, \(\Delta t\), used in the numerical solution of the models. We observe that in order to get an error of 3% or lower in all cases, we need a time step of \(\Delta t = 10\;\upmu\)s or smaller. Note that for the EMI model, the operator splitting algorithm used to solve the system of equations23,41 is unstable when the two largest considered time steps are used for the default value of \(R_g\).

Spatial resolution

In the right panel of Fig. 2b, we investigate the effect of the spatial resolution, \(\Delta x\), used in the model meshes. Note here that for KNM and SKNM, there is no tuneable spatial discretization parameter since the location of the cells dictates the node points. Note also that for EMI, a relatively fine mesh (\(\Delta x\) = 20 μm) is needed merely to represent the geometry of the cells and the surrounding extracellular space, so no larger values of \(\Delta x\) are considered. Furthermore, to achieve an error smaller than or equal to 3%, a 5 μm resolution seems to be required for the EMI model. For BD and MD, the errors associated with choosing a large value of \(\Delta x\) seems to be most pronounced for increased values of \(R_g\). Moreover, in order to make the error smaller than 3% for all the considered values of \(R_g\), a resolution of 10 μm appears to be needed for BD and MD.

Comparison of model solutions for EMI, KNM, SKNM, BD and MD

Figure 3
figure 3

Properties of the action potentials computed using EMI, KNM, SKNM, BD and MD. In the first row, we show the membrane potential in the center of cell number 10 for the same type of simulations as those reported in Fig. 2 for KNM, SKNM and EMI. In the second row, we similarly show the membrane potential for BD, MD and EMI. The timing is adjusted for each model such that \(t=0\) ms is the time when the membrane potential has increased by 10% of the action potential amplitude during the action potential upstroke. Note that the SKNM, KNM and EMI solutions are indistinguishable in these plots. In addition, the BD and MD solutions are indistinguishable from each other, but different from the SKNM, KNM and EMI solutions. In the third row, the action potential duration at 90% repolarization, APD90, is displayed for all five models. In the simulations, we use \(\Delta x = 3\;\upmu\)m for EMI, BD and MD, and \(\Delta t = 1\;\upmu\)s for all models.

Full size image

In Fig. 2c, the CV computed using the finest resolution of all the considered models (EMI, KNM, SKNM, BD, and MD) are reported for three values of the gap junction resistance, \(R_g\). Here we observe that the CVs computed using all five models are quite similar for the default value of \(R_g\). However, when \(R_g\) is increased, EMI, KNM and SKNM appears to be very similar, and BD and MD are very similar, but there are some differences in the CV between these two groups of models, consistent with what was found in earlier studies7,34.

In Fig. 3, we display properties of the action potentials computed using each of the five models. In the upper row, we observe that the computed action potentials for EMI, KNM and SKNM are indistinguishable both for the default case (\(1\times R_g\)), and in cases of increased \(R_g\). Similarly, in the second row, we show that the action potentials computed using BD and MD are also almost indistinguishable from the EMI model solution for the default value of \(R_g\). In the cases of increased \(R_g\), however, the first part of the depolarization seems to be considerably slower for the EMI model than for BD and MD, consistent with the slower conduction velocity for EMI compared to BD and MD observed in Fig. 2. In addition, the initial fast repolarization following the upstroke of the action potential (the action potential notch) seems to be more pronounced for EMI than for BD and MD in the weakly coupled cases (\(50\times R_g\) and \(200\times R_g\)). On the other hand, the action potential duration seems to be very similar for all the considered models. Indeed, in the lower part of Fig. 3, we observe that the action potential duration at 90% repolarization, APD90, is 285.7 ms for all five models, and for the weakest coupled case (\(200\times R_g\)), the difference in APD90 between MD, BD and EMI, KNM, SKNM is only about 3 ms.

Figure 4
figure 4

Simulations of a small domain with an infarction scar and border zone. (a) Snapshots of the solutions at four points in time after a stimulation is applied for EMI, KNM, SKNM, BD and MD. (b) CPU efforts of the simulations in terms of number of nodes, number of time steps and CPU time required to run a 40 ms simulation. (c) Applied domain set-up. Each cell is represented by a small colored rectangle. The pink area represents healthy tissue, the blue area represents infarction border zone and the purple area represents the scar core. The yellow area marks the stimulation site (in the healthy region), and the turquoise point marks a measurement point used in (d). The tissue consists of 13 × 65 cells and is 1.3 mm × 1.3 mm. (d) Point in time when the membrane potential in the turquoise point in (c) reaches \(v\ge\) 0 mV for each of the five models. We use \(\Delta x = 5\;\upmu\)m for EMI, \(\Delta x = 10\;\upmu\)m for BD and MD, and \(\Delta t = 10\;\upmu\)s for all models.

Full size image

Infarcted region

In Fig. 4, we further investigate the difference between the models using an example application of a small infarction scar. Figure 4c shows the set-up used in the simulation. We consider a collection of 13 × 65 cells, and each of the small rectangles in Fig. 4c represents a cell in the tissue. The volume of each cell is about 30 pL, see Fig. 1. The pink and yellow areas both represent healthy tissue, and a stimulation current is applied in the yellow area. The purple area represents the scar core. Here, the gap junction resistance, \(R_g\), is set to infinity and the conductance of the sodium channels, \(g_{\textrm{Na}}\) is set to zero, representing injured, non-conductive tissue. The blue area surrounding the scar represents the scar border zone. In this area, the extracellular potassium concentration and the gap junction resistance are increased compared to the healthy case. More specifically, \(R_g\) is increased by a factor linearly increasing from 50 at the outer part of the border zone to 200 at the inner part. Similarly, the extracellular potassium concentration increases linearly from 5.4 to 10 mM from the outer to the inner parts of the border zone. The simulation set-up is motivated by the problem suggested in Ref. 38 and refined in Ref. 39.

In Fig. 4a, we show snapshots of the solution of all the five models (EMI, KNM, SKNM, BD, and MD) at four points in time after stimulation is applied for a simulation using this set-up. When the excitation wave travels in the healthy part of the tissue (two leftmost panels), all five models appears to provide very similar solutions. However, as the wave reaches the high-resistance border zone (rightmost two panels), the wave clearly travels faster for BD and MD than for EMI, KNM and SKNM. Moreover, Fig. 4d shows the point in time after the stimulation was applied when the membrane potential in the turquoise point in Panel c first reaches a membrane potential above 0 mV. We observe that this time of arrival (ToA) is quite similar for EMI, KNM and SKNM, and similar for BD and MD, but that the ToA differs between the two groups of models.

Comparison of CPU times for EMI, KNM, SKNM, BD and MD

In Fig. 4b, we report the number of mesh nodes, number of time steps and total CPU time for a 40 ms simulation for each of the five models. We observe that the CPU time for SKNM (3 s) is a bit shorter than the CPU time for KNM (7 s) and considerably shorter than the CPU time for EMI (16 h). Since the solution of these three models appears to be very similar, we will use SKNM as a representative model for EMI and KNM. Similarly, the CPU time for MD (4 min) is quite a bit shorter than that of BD (28 min), and we will therefore use MD as a representative model of MD and BD in simulations of a larger domain.

Speedup for the EMI model

Motivated by the fact that the CPU time for the EMI model is considerably longer (16 h) than for the other models (3 s–28 min), we have attempted to speed up the EMI model simulations by enabling a larger degree of parallelization than what is used in the default implementations of the models (see the Supplementary Information). Details of this speedup are found in the Supplementary Information. Using the optimized EMI code, the simulation displayed in Fig. 4 takes 2 h and 11 min to run on a 24-core AMD Epyc 7413 CPU. This constitutes a total speedup factor of 7.6 compared to the unoptimized code with the same number of threads on the same hardware, which takes 16 h and 41 min.

Comparison of SKNM and MD solutions around an infarction scar

Figure 5
figure 5

Simulations of SKNM and MD for a 1 cm × 1 cm domain with an infarction scar and border zone. (a) Snapshots of the solutions at four points in time after a stimulation is applied. (b) Applied domain set-up. The pink area represents healthy tissue, the blue area represents infarction border zone and the purple area represents the scar core. The yellow area marks the stimulation site (in the healthy region), and the turquoise point marks a measurement point used in (c). The tissue consists of 100 × 500 cells and is 1 cm × 1 cm. (c) Point in time when the membrane potential in the turquoise point in (b) reaches \(v\ge\) 0 mV for the two models. We use \(\Delta x = 10\;\upmu\)m for MD and \(\Delta t = 10\;\upmu\)s for both models.

Full size image

Using SKNM as a representative model for EMI, KNM and SKNM and MD as a representative model for BD and MD, the simulations of Fig. 4 are repeated for a larger domain in Fig. 5. The set-up is similar to that illustrated in Fig. 4c, except that the radius of the scar core is increased to 2 mm and the width of the surrounding border zone is set to 1.5 mm (see Fig. 5b). The total domain consists of 100 × 500 cells and is 1 cm × 1 cm. The scar core and border zone are treated in the same manner as in the simulations reported in Fig. 4, except that the gap junction resistance increases by a factor from 20 to 200 instead of from 50 to 200 from the outer to the inner parts of the border zone. In the figure, we observe that there seems to be a significant difference in the time of arrival (ToA) between SKNM and MD also in this case of a larger domain.

Reentrant wave generated for SKNM, not for MD

To illustrate that the differences in conduction velocity (Fig. 2c) and time of arrival (Figs. 4d, 5c) between the cell-based models (EMI, KNM, SKNM) and the homogenized models (BD, MD) can significantly influence the simulation results, we further use SKNM and MD to investigate the tissue’s susceptibility to reentry for the two groups of models. To this end, we apply a classical S1-S2 stimulation protocol (see, e.g., Refs.42,43). The S1 stimulation is applied in 3 × 5 cells in the lower center of the domain like illustrated in Fig. 5b, and the S2 stimulation is applied 310 ms later in the entire lower left quarter of the domain (except for in the scar core).

Figure 6
figure 6

Reentrant wave generated around an infarction scar for SKNM, but not for MD. Reentry is attempted to be generated by applying an S1-S2 stimulation protocol42,43. The S1 stimulation is applied in the lower part of the domain (see Fig. 5b), and the S2 stimulation is applied in the lower left quarter of the domain (except for in the scar core) 310 ms after the S1 stimulation was applied. The time points at the top of the plots report the time after the S2 stimulation was applied. In the border zone, the extracellular potassium concentration increases linearly from 5.4 mM at the outer part to 10 mM in the inner part. Furthermore, \(R_g\) is increased by a factor that similarly increases linearly from 20 to 200. We use \(\Delta x = 10\;\upmu\)m for MD and \(\Delta t = 10\;\upmu\)s for both models.

Full size image

In Fig. 6, we show snapshots of the solution of SKNM and MD at five points in time after the S2 stimulation was applied in an infarction scar simulation using this set-up. We observe that for SKNM, a wave is generated traveling around the scar core in the counter-clockwise direction. Directly following the S2 stimulation, the wave is not able to move in the clockwise direction because the cells above the stimulation site are not yet depolarized. When the wave reaches the area of the S2 stimulation after traveling one round, however, the tissue is depolarized enough for the wave to continue traveling around the scar core and we get a reentrant wave around the scar core.

For MD, on the other hand, the S2 stimulation induces a wave traveling both in the clockwise and counter-clockwise directions. This may be explained by the fact that the CV is faster for MD than for SKNM (Figs. 2c and  5a), and that the excitation wave following the S1 stimulation has traveled so fast that the tissue above the S2 stimulation area is able to depolarize again following the S2 stimulation. Since the wave travels in two directions, there is no tissue ready to be depolarized again after the wave has traveled through the entire border zone and healthy tissue, and, consequently, no reentrant wave is generated for MD.

Reentrant spiral wave in the border zone for SKNM and MD

In Fig. 6, we observed that a reentrant wave was generated around the scar core for SKNM, but not for MD. However, using another choice of parameters, a reentrant spiral wave is generated in the border zone for both models (see Figs. 7 and 8). In this case, we let the gap junction resistance be increased by a factor ranging from 20 to 375 in the border zone instead of from 20 to 200 (linear increase from outer to inner parts of the border zone).

Figure 7
figure 7

SKNM simulation of a reentrant spiral wave in the border zone. We apply an S1-S2 stimulation protocol42,43. The S1 stimulation is applied in the lower part of the domain (see Fig. 5b), and the S2 stimulation is applied in the lower left quarter of the domain (except for in the scar core) 310 ms after the S1 stimulation was applied. The time points at the top of the plots report the time after the S2 stimulation was applied. In the border zone, the extracellular potassium concentration increases linearly from 5.4 mM at the outer part to 10 mM in the inner part. Furthermore, \(R_g\) is increased by a factor that similarly increases linearly from 20 to 375. We use \(\Delta t = 10\;\upmu\)s.

Full size image

In Fig. 7, we show the activity following the S2 stimulation in the SKNM simulation. We observe that for the first 600 ms, a reentrant wave similar to that observed in Fig. 6 is generated traveling around the scar core. After this, the reentrant wave in the healthy tissue seems to dissipate, while a small reentrant spiral wave continues in the border zone. After some time (at 1150 ms after the S2 stimulation), this electrical activity in the border zone spreads to the healthy tissue and depolarizes it. Interestingly, the activity in the border zone continues even after the cells in the healthy tissue repolarize again and after some time (at 1600 ms and at 1980 ms) new waves spread from the border zone to the healthy tissue.

Figure 8
figure 8

MD simulation of a reentrant spiral wave in the border zone. The simulation set-up is the same as that used in Fig. 7. We use \(\Delta x = 10\;\upmu\)m and \(\Delta t = 10\;\upmu\)s.

Full size image

In Fig. 8, the same simulation is conducted using MD. We observe that even though there are significant differences between the SKNM and MD solutions (Figs. 7 and  8), there are also qualitative similarities between the solutions. For example, Fig. 8 shows that in this case, like for SKNM, a small reentrant spiral wave is generated in the border zone also in the MD solution. Furthermore, like in the SKNM simulation, excitation waves are repeatedly emitted from the border zone to the healthy tissue.

Modeling capability exclusive to EMI—effect of a non-uniform distribution of ion channels on the cell membrane

Figure 9
figure 9

Comparison of a uniform (U) and non-uniform (NU) distribution of L-type calcium channels in a single-cell EMI model simulation. (a) Illustration of the uniform and non-uniform distributions of L-type calcium channels in the EMI model membrane mesh. (b) Action potentials computed using the EMI model for the two channel distributions, U and NU. We use \(\Delta x\) = 1 μm and \(\Delta t = 10\) μs. The membrane potential is plotted for three membrane points (one at each cell end and one in the center of the cell) for each of the channel distributions, but the solutions for the different membrane points are indistinguishable.

Full size image

In Figs. 2, 3, 4, we observed that KNM and SKNM provided good approximations of the EMI solution. Nevertheless, in some cases, the improved complexity of EMI makes the model able to accurately represent properties that cannot be represented in the more simple KNM and SKNM. One example of such an application is illustrated in Fig. 9. In this case, we consider the case of a non-uniform distribution of ion channels along the cell membrane. More specifically, we compare the case when all the L-type calcium channels are uniformly distributed throughout the membrane (U), to the non-uniform (NU) case where the channels are located in five bands along the length of the cell (see Fig. 9a). Figure 9b shows the action potentials computed in single-cell EMI model simulations using these two channel distributions, and we observe that the duration of the action potential is considerably reduced in the NU case.

Discussion

Our aim was to provide a comparison of five different models of cardiac electrophysiology in terms of computational efficiency and physiological resolution. We compared the classical bidomain model (BD), the monodomain model (MD), the recently developed Kirchhoff network model (KNM), the associated simplified Kirchhoff network model (SKNM), and the extracellular-membrane-intracellular model (EMI) for a set of classical test cases. The biomarkers used for assessing the properties of the methods are the conduction velocity (CV) and the action potential duration (APD). Both of these biomarkers are well-known to be important characteristics in the analysis of possible arrhythmias, see, e.g., Refs.44,45,46,47,48 for CVs and Refs.19,49,50,51,52 for the APDs.

Computational efficiency

The five considered models are different in their basic construction. The classical BD and MD models are developed by averaging over many cardiomyocytes and the models assume that the extracellular space, the intracellular space and the cell membrane all exist everywhere. This represents a colossal simplification of the models in terms of software implementations and computing efforts but clearly limits the models’ validity when the spatial scale is refined towards the size of individual cardiomyocytes. KNM and SKNM are based on representations of individual cells and are as such refining the physiological accuracy compared to BD and MD. Finally, the EMI model is clearly the most detailed one since it represents the cardiomyocytes at the sub-cellular level.

In Fig. 2 we compare the spatial and temporal resolutions needed to obtain convergence of the five models. We define convergence to be achieved if the error in the conduction velocity is less than 3%, where the error is computed by comparing the solution obtained by a solution computed with a very fine numerical resolution. The comparison is performed for several values of the cell-to-cell resistance and we note that more resistance requires finer spatial resolution for MD, BD and EMI. However, for KNM and SKNM, the spatial resolution is fixed since it is defined by the cell size; these models do not contain a \(\Delta x\) parameter to be tuned. For EMI, the spatial resolution needed is \(\Delta x=5\;\upmu\)m, while 10 μm appears to be sufficient for BD and MD.

It should be noted that the spatial resolution required for the classical BD and MD models is significantly finer than the meshes frequently used in BD and MD tissue simulations. Standard resolutions appear to be about \(\Delta x \approx 0.25\) mm, see, e.g., Refs.13,53,54,55,56. This means that for 1 cm\(^3\) cardiac tissue, the number of computational nodes would increase from \(\sim 64,000\) in the standard resolution, to one billion in the resolution indicated here. Clearly, this has enormous consequences for the computational demands of the BD and MD models, and we need to emphasize that we do not suggest as a general rule that \(\sim 10\;\upmu\)m is necessary for convergence of these models. However, close to infarcted regions, such resolutions appear to be necessary in order to properly compute a converged conduction velocity.

Also, the temporal resolution is estimated using the same criterion. For all models, \(\Delta t=10\; \upmu\)s is sufficient to reach convergence for the numerical methods used in our computations.

For the challenging case of simulating conduction in the vicinity of an infarcted region, Fig. 4 clearly states that the SKNM method solves the test problem to convergence fastest (3 s) followed by KNM (7 s), MD (4 min), BD (28 min) and EMI (16 h). In the Supplementary Information we showed that the computing efforts of the EMI model could be significantly reduced by parallelizing the code and further improving its performance, but the model is still much more computationally intensive than the other four, especially compared to KNM and SKNM.

In terms of computational efficiency, SKNM and KNM appear to be very well suited for challenging tissue simulations at small volumes, but the models will be demanding for large volumes since every cardiomyocyte is represented in the model. BD and MD become computationally demanding for challenging tissue simulations but are known to be relevant models, and in fact the only viable option, for large tissues. The optimized utilization of multicore computers for solving BD equations has been analyzed in various studies, as discussed in Refs.57,58. Similar analyses have been conducted for the MD equations, see, e.g., Refs.59,60. The EMI model is very accurate but extremely costly in terms of computations and can only be applied when relatively few cells are considered.

Implications for simulating post-infarct arrhythmias

Myocardial infarction induces complex cardiac remodeling such as infiltration of fibrotic tissue61, up or down regulation of membrane ion channels62,63, as well as repositioning of these channels around the cell membrane64. While some of these changes can be represented in classical BD/MD formulations through modifications in action potentials and conduction velocities, the finer changes occurring in the cellular scale are lost in these spatially averaged models. This uncertainty has been previously reported in modeling studies using BD/MD formulations which have shown that the inducibility of post infarct reentry is highly sensitive to the conduction velocity parameters chosen to represent the infarct border zone39,65. Figure 6 shows that the faster conduction velocity in the border zone of the MD model results in decreased reentry inducibility as compared to the SKNM model.

Further decreasing the conduction velocity in the border zone resulted in the induction of qualitatively similar reentrant activity in both the MD and SKNM models. Both models resulted in micro-reentrant circuits initiated and maintained within the border zone region. Such complex reentry morphologies have been previously observed in MD simulations that incorporate complex fibrosis within the border zone66. While micro-reentrant circuits are difficult to observe experimentally due to limitations in resolution of recording devices, it has been postulated that micro-reentrant circuits could underlie ectopic activity that have been frequently observed in post-infarction hearts67.

Fine scale simulations

The cell-based models KNM and SKNM approximate the solutions of the more precise EMI model very effectively when cell-based accuracy suffices. However, in cases where resolution of individual cells is necessary, BD, MD, KNM, and SKNM all fall short, necessitating the application of the EMI model. For instance, it is well established that the ion channels carrying the sodium current are distributed in a highly non-uniform manner on the membrane of cardiomyocytes37,68,69. In order to properly represent this effect in a model, sub-cellular resolution of the cell membrane is needed. In Ref. 18, the distribution of sodium channels was analyzed using the EMI model and it was found that the distribution of sodium channels significantly influenced the conduction velocity of the excitation wave. The effect of non-uniform distribution of other ion channels was analyzed in Ref. 70 using EMI. It was found that only the distribution of sodium channels had a significant effect on the conduction velocity.

Here, we analyzed the effect of a non-uniform distribution of the L-type calcium channels, see Fig. 9, and we found that the distribution significantly affected the action potential duration of the excitation wave. Such investigations would not be possible to conduct using BD, MD, KNM, or SKNM, since the individual cells are not spatially resolved in those models. The physiological motivation for this case is that the L-type calcium channels are mainly present in a system of t-tubules of the cardiomyocytes which forms a banded structure along the cell membrane. Note that the representation given in Fig. 9 is merely meant to illustrate the kind of analysis enabled by the EMI model, and it specifically does not represent the rather complex geometrical structure of t-tubules.

The EMI model can also be used to study ephaptic effects11,18,71 and also the effect of objects close to the cell on the extracellular potential20. For studies of ephaptic effects close to individual ion channels, the more challenging Poisson-Nernst-Planck equations need to be applied72. In that model, even the thickness of the cell membrane must be represented and the EMI framework is thus not directly applicable. If electroneutrality is assumed, concentration of individual ions can also be modeled using the KNM-EMI approach15,73.

Recent literature74,75 proposes advancements to the MD model, prompted by the necessity to capture stark regional variances in conductive attributes due to fibrosis. Additionally Ref. 75, introduces a non-linear Ohmic conductance to address the phenomena associated with markedly slow conduction. Although these are further developments of the MD framework, cellular structures are still omitted from the modeling. Consequently, comparing these models with the EMI model could illuminate the precision of such homogenized approaches.

Conclusion

We have compared five mathematical models of cardiac electrophysiology (BD, MD, KNM, SKNM, EMI) with respect to computational requirements and physiological resolutions. The classical BD and MD models are well suited for simulating large tissues where many cells can be represented by averages. For cell-based accuracy, KNM and SKNM are well suited since every cell is explicitly represented in the simulation. If the impact of varying the density of ion channels along the membrane of individual cardiomyocytes or ephaptic coupling are to be studied, the EMI model is the only viable alternative. On the other hand, the EMI model cannot, at present, be applied to large tissues because of the associated computational load.