Introduction

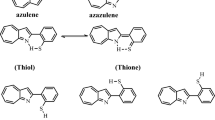
Azaazulenes, an azulene heterocyclic analogue (Fig. 1), have attracted concern due to their chemical and physical properties and their biological activity1,2 as anticancer agents3. 1-azaazulenes are the most stable of the several azaazulene structures. When nitrogen and oxygen (sulphur) atoms in the heterocyclic ring change hydrogen atoms, tautomers are produced. The proton transfer and hydrogen bonding of the hydrogen atom are significant properties in chemistry. As a result, equilibrium between (enolimines/thiol and ketoenamines/thione forms) of 2HPhAZ and 2MPhAZ tautomeric forms is expected (Fig. 1).

Figure 1
figure 1

The tautomeric structure (enolimines/thiol and ketoenamines/thione form) of 2HPhAZ and 2MPhAZ.

Full size image

Understanding the relative stabilities of tautomeric forms and their mutual conversion is a crucial topic from the standpoint of structural chemistry. Oda et al.4 demonstrated that spectroscopic and X-ray crystallographic investigations supported the structure of 2OHPhAZ. A reasonably substantial absorption in the visible light spectrum, as well as the X-ray diffraction data4, support the presence of its aromatic and coplanar nature and an intramolecular hydrogen bond. The stability of 2OHPhAZ, the keto tautomer (2OPhAZ), and various rotamers (2OHPhAZ-R1:R3) in the gas phase and ethanol was the subject of DFT research by El-Meligy et al.5. Furthermore, to the best of our experience, we have not found any analysis of the nature of the bonding in the tautomerization of 2-(2-Hydroxyphenyl)-1-azaazulene (2HPhAZ) and its mercapto analogue 2-(2-Mercaptophenyl)-1-azaazulene (2MPhAZ).

The study of covalence and hybridization effects in polyatomic wave functions led to the development of the natural bond orbital (NBO) analysis method. The work of Foster and Winhold6 was expanded by Reed et al.7, who utilized NBO analysis that showed mainly H-bonded and other strongly bound van der Waals complexes. The "natural Lewis's structure" has filled NBOs that are excellently suited to describing covalency effects in molecules7. However, the general conversion to NBOs also produces orbitals that are vacant in the official Lewis structure and can be utilized to characterize non-covalent effects.

The terms filled and unfilled orbitals of the formal Lewis structure are denoted, respectively, by the symbols σ and σ*, though the former orbitals may be core orbitals (CR), lone pairs (LP), σ or π bonds (σ, π), and so forth, and the latter may be σ or π anti-bonds (σ*, π*), extra valence shell Rydberg (RY*) orbitals.

The NBO analysis focuses on the availability of a device of high quality, shedding light on both the HB-related electron delocalization-induced hyper conjugative effects and the many effects found to influence the NH-stretch spectral shift, i.e., the main measurable quantity on which most of the spectroscopic approaches are based.

The aim of this study is complementary to our work which is published in omega and Scientific reports journals5,8 to complete our work in this point that we study with the Natural Bond Orbital property to find the mechanism of the stability of the tautomer and rotamers of 2-hydroxyl phenyl azaazulene and -mercapto phenyl azaazulene.

In the current work, we attempt to investigate the electronic structure, stabilities, and bonding characteristics of the 2HPhAZ and 2MPhAZ tautomers and rotamers in gas phase and ethanol at the theoretical level B3LYP/6–311 +  + G(2d,2p). The hybridization of each atom, natural charges (Core, Valence, and Rydberg), the second order perturbation energy (E (2)) of bonding and antibonding orbitals, exact configurations, and Lewis and non-Lewis's electrons have all been considered in the study of the results from natural bonding orbital analysis in gas phase and ethanol.

Computational details

The gradient-corrected hybrid density functional B3LYP/DFT approach was used for all computations9,10. Using this functional10 and the 6–311 +  + G (2d, 2p) basis sets11 as implemented in the Gaussian 09 program12, a comprehensive geometry optimization without symmetry constraints was carried out for each structure. Both Gauss View 5.0.913 and Chem-Craft 1.614 were used to visualize all geometries. The natural bond orbital approach15 has also been used to perform the population analysis at the B3LYP/6–311 +  + G (2d, 2p) level of theory using the Gaussian 09 software package. In this process, sets of natural atomic orbitals (NAOs), natural hybrid orbitals (NHOs), and natural boundary orbitals (NBOs) are successively changed from non-orthogonal atomic orbitals (AOs).

Since electron density and other attributes are defined by the fewest number of filled orbitals in the fastest-convergent manner, all these localized basis sets are complete and define the wavefunctions in the most practical manner. The second-order perturbation interaction energy (E(2)), which is defined using the NBO technique, can be used to quantitatively explain this noncovalent bonding-antibonding interaction16,18,18. The estimation of the off-diagonal NBO Fock matrix elements is represented by this energy. From the second-order perturbation method, it may be inferred15.

$$E^{{({2})}} = \Delta E_{{{\text{ij}}}} = q_{i} (F(i{\text{j}})^{{2}} /\varepsilon_{j} {-}\varepsilon_{i} ),$$
(1)

where qi is the donor orbital occupancy, εi and εj are diagonal elements and (ij) is the off-diagonal NBO Fock matrix element.

Result and discussion

Geometry optimization

Figure 2 lists the tautomeric structures of 2HPhAZ and 2MPhAZ (enolimines/thiol and ketoenamines/thione forms). Table 1 lists all the optimized structural properties determined in gas phase, and ethanol at the B3LYP/6–311 +  + G(2d,2p) level of theory. Table 1 shows that the bond lengths in the tautomeric structure of 2HPhAZ (enolimines and ketoenamines form) are shorter than those in the thiol and thione forms of the mercapto homologue, but the estimated bond angles have shown the opposite in both gas and ethanol phases. The mercapto analogue's bond angles are less than those of hydroxy structures. Additionally, it has been discovered that the HB length of the N–H–O(S) and the C–N–H bond angle are longer and smaller for the thiol and thione forms than the enol and keto forms, respectively. The chemical differences between sulfur and oxygen atoms are to blame for that. The longest hydrogen bond, O(S)…H, is between the enol and thione forms. The R3(O) and R3(S) rotamers have the longest O(S)–C bonds among them. The R2(O) and R2(S) produce the biggest C–O(S)–H bond angle by rotating the phenyl ring. An intriguing feature to note is how the bond length and angle change when the tautomeric structure's σF values change19,21,21. i.e., σF is the value of change in factor of the bond length and bond angle when adding any para substituent on the benzene ring; in this case (our compounds), when changed to the tautomeric structures of 2HPhAZ and 2MPhAZ compounds, the value of factor of the bond length and bond angle are changed.

Figure 2
figure 2

The optimized structural for the tautomers and rotamers of 2HPhAZ and 2MPhAZ at B3LYP/ 6–311 +  + G(2d,2p) level of theory.

Full size image
Table 1 The selected bond lengths in angstrom (Å) and angles in degrees (◦) calculated for the tautomer and rotamers structures of 2HPhAZ and 2MPhAZ in gas phase, and ethanol using B3LYP/ 6–311 +  + G(2d,2p) level of theory.
Full size table

Electronic structure

Enolimines/thiol and ketoenamines/thione are the two π-isoelectronic (tautomeric) structures in which the 2HPhAZ and 2MPhAZ are found. Additionally, research has been done on the three rotameric forms (R1, R2, and R3). DFT calculations at B3LYP/ 6–311 +  + G(2d,2p) level of theory to determine which form is more stable at the ground state by doing frequency calculations at the same level of calculation, the optimized geometry of the investigated tautomeric structure was verified as a minimum on the potential energy surface. Figure 2 shows the optimized structure for the investigated tautomeric structure.

The C1 symmetry point group is where the optimization structures are found (supporting information). Table 2 displays the total energy and relative energy of the tautomeric and rotameric structures calculated at the B3LYP/6–311 +  + G(2d,2P) in gas and ethanol phases. In case of 2HPhAZ, the studied DFT method qualitatively gives similar tautomer stability orders in the gas phase and ethanol. The ethanol solvent causes some reordering of the relative stability of 2MPhAZ conformers.

Table 2 Relative zero-point corrected energies (ΔE0, kJ/mol), and the energy gap (Eg), for the tautomer and rotamers structures 2HPhAZ and 2MPhAZ in gas phase, and ethanol at B3LYP/ 6–311 +  + G(2d,2p) level of theory.
Full size table

For tautomerization, the thiol form was found to be more stable than the thione form in the gas phase. The relative energy difference between thiol and thione in the gas phase is 5.253 kJ at B3LYP/6–311 +  + G(2d,2P). Stabilization of thiol in the gas phase is expected by the presence of a lower and stronger IHB of thione.

On the energy scale, the tautomeric structures are present in a static mixture in the ground state, with the enol form being (29.492 and 7.737 kJ) more stable than the keto form in gas phase and ethanol, respectively (Table 2). It has been found that keto/thione form has the lowest HOMO–LUMO gap (2.275/1.852 eV) followed by enol/thiol forms (3.098/2.980 eV).

In the ground state of rotamers in statical mixes, the R3(O) structure is more stable than the R2(O) and R1(O) structures, but the R1(S) structure is more stable than the R3(S) and R2(S) structures (Table 2). The stability of R2(O) and R3(O) can be attributed to the possible intramolecular H bonding interaction of the C–H…N as shown in Fig. 2. The slightly higher stability of R3(S) than R2(S) can be due to the anti-position present between the S26-H28 group and the nitrogen of the azaazulene ring, given the possibility of H28 interaction with the sulfur atom. The highest gap is in the rotamers. It is widely known that a molecule's reactivity increases with decreasing energy gaps22,23. As a result, it is anticipated that the keto/thione form will be more chemically reactive than enol/thiol and their rotamer. The keto/thione compound can function as both an electron acceptor and donor. The results of the MO calculation show that the computed reactivity in the gas phase and ethanol of the studied compounds increases in the order.

For 2HPhAZ, enol > keto > R3(O) > R2(O) > R1(O) in gas phase but in ethanol the order of stability is Enol > keto > R1(O) > R2(O) > R3(O).

In case of 2MPhAZ, thiol > thione > R1(S) > R3(S) > R2(S) in gas phase. In ethanol, the order of stability becomes thione > thiol > R1(S) > R3(S) > R2(S) in 2MPhAZ. Our results are agreeing with the previous results that of 2-(2-Hydroxyphenyl)-1-aza azulene and 2-(2-Mercaptophenyl)-1-aza azulene5,8.

Character of natural hybrid orbital (NHO) on the tautomeric structure

A natural atomic orbital (NAO) is a valence-shell atomic orbital that was created by diagonalizing the localized block of a given molecule's full density matrix, is connected to the atom in question via basis functions Xi (A), and simultaneously satisfies the orthonormality and maximum occupancy conditions. While NAOs in a single atom simply coincide with natural orbitals, in polyatomic molecules they largely maintain their one-center nature (as opposed to natural orbitals, which get delocalized over all nuclear centers). Since a single center in polyatomic molecules is surrounded by a molecular electron density, NAOs is regarded as offering the best explanation of this position. Additionally, an NHO is produced via a unitary transformation of a directed hybrid orbital that is symmetrically orthogonalized and centered on a specific atom. Finally, an NBO is an orbital produced from NHOs in the simple bond orbital diagram. Thus, for a localized σ-bond between atoms A and B, the NBO is defined as:

$$\sigma_{{{\text{AB}}}} = C_{{\text{A}}} h_{{\text{A}}} + C_{{\text{B}}} h_{{\text{B}}}$$
(2)

where hA and hB are the natural hybrids centered on atoms A and B. Therefore, the NBOs thoroughly agree to the representation of localized bonds and lone pairs as basic units of molecular structure, and hence it will be probable to handily take ab initio wavefunctions in terms of the classical Lewis structure concepts by converting these functions to the NBO forms24. In Table 3, we produce the resulting natural atomic hybrids hA on some atoms with the polarization coefficient CA for each hybrid (in explanations) in the equivalent NBO. The assessment of the results described in Table 3 in gas phase, and ethanol shows that:

Table 3 Calculated natural hybrid (NHOs) and the polarization coefficient for each hybrid in the equivalent NBO (in explanations) for the studied the tautomers and rotamers structures of 2HPhAZ and 2MPhAZ in gas phase, and ethanol at B3LYP/6–311 +  + G(2d,2p) level of theory.
Full size table

The p characteristics of sulfur NHO σC25-S26 and nitrogen NHO σC15-N16 bond orbitals increase with increasing Hammett constant in gas phase, and ethanol due to stretching of the C25-S26 bond of the thiol and thione tautomer. The C25-O26 bond of enolimines and ketoenamines tautomers shortens, in gas phase, and ethanol causing orbitals to contract with increasing Hammett constant, in contrast to the p characteristics of oxygen NHO σC25-O26 and nitrogen NHO σC15-N16. While the predicted d contributions of S atoms, which are insignificant and nearly equal, determine that 3d orbitals are not important for the bonding of the thiol and thione tautomer in gas phase, and ethanol.

The O(S)-C sigma bond's interaction becomes weaker. These compounds exhibit strong delocalized nO(S) —> σ*C25-O26(S26) and nO(S) —> σ*C15-N16 as well as significant hyper conjugative interaction, which results in partial p character (Table 4). Additionally, Table 4 shows that E(2) rises in gas phase, and ethanol when the investigated compounds' Hammett constants rise, extending the (O)S-C bond as a result. Table 2's stability order reveals that the enol/thiol structure has higher Relative zero-point corrected energies (ΔE0, kJ/mol), values than the keto/thione structure in gas phase. The enol and thiol structure being more stable than the keto and thione structures in gas phase. The ethanol solvent causes some reordering of the relative stability of 2HPhAZ and 2MPhAZ conformers. The relative energy difference between thiol and thione in the gas phase is 5.253 kJ at B3LYP/6–311 +  + G (2d,2P). For rotamer, R3(O) structure have higher stability than R2(O) and R1(O) structures, while R1(S) structure has higher stability than R3(S) and R2(S) structures (Table 2).

Table 4 Second order delocalization energies (E(2)) for the studied compounds in gas phase, and ethanol at B3LYP/6–311 +  + G(2d,2p) level of theory, all values are in kcal/mol.
Full size table

Donor–acceptor (bond–anti-bond) interactions

Each valence bonding NBO (σAB) in the NBO analysis24 must be coupled with a corresponding valence antibonding NBO (σ*AB), to compute the span of the valence space:

$$\sigma *_{{{\text{AB}}}} = C_{{\text{A}}} h_{{\text{A}}} - C_{{\text{B}}} h_{{\text{B}}}$$
(3)

For example, the Lewis σ-type (donor) NBOs are matched by the non-Lewis σ*-type (acceptor) NBOs that are properly vacant in an ideal Lewis structure picture. The universal transformation to NBOs leaves vacant orbitals in the formal Lewis structure. As a result, the filled NBOs of the natural Lewis's structure can accurately reflect covalency effects in molecules. Given that the non-covalent delocalization effects are linked to σ — > σ* interactions between filled (donor) and empty (acceptor) orbitals, it is only logical to refer to them as being of the donor–acceptor, charge transfer, or generalized "Lewis's base-acid" Lewis's type. The anti-bonds reflect unutilized valence-shell capacity and span areas of the atomic valence spaces that are formally unsaturated by covalent bond formation. Weak occupancies of the valence anti-bonds represent actual "delocalization effects," or irreducible deviations from the idealized localized Lewis picture. To account for the donor–acceptor (bond-anti-bonds) interactions, all potential interactions between "filled" (donor) Lewis-type NBOs and "empty" (acceptor) non-Lewis NBOs are examined in the NBO analysis. The energies of these interactions are then estimated using second-order perturbation theory. These interactions (or energy stabilization) are referred to as "delocalization" corrections for the zeroth-order natural Lewis structure.

Table 5 reports the most significant interaction between "unoccupied" (acceptor) non-Lewis NBOs and "occupied" (donor) Lewis-type NBOs. The lp (S or O) participates as a donor and the BD*(O(S)-C) anti-bond as an acceptor [lp (S or O) — > BD*(O(S)-C)], with charge transfer energy values at the B3LYP level. These results of the NBO analysis are collected in Table 5 in gas phase, and ethanol. This shows that increasing the Hammett constants of these studied compounds leads to a decrease in charge transfer energy. It may be concluded that the strength of the O(S)-C bond only minimally changes in the studied compounds because the amount of destabilization energy predicted using the NBO technique does not significantly alter in each of the compounds, which is consistent with our calculated results5 and the experimental results25.

Table 5 The second-order perturbation energies E(2) (kcal/mol) corresponding to the most important charge transfer interactions (donor — > acceptor) in the studied compounds in gas phase, and ethanol by using B3LYP/6–311 +  + G(2d,2p) method.
Full size table

The calculated natural orbital occupancy, repeatedly known as the orbital's "natural population," is shown in Table 6 in gas phase, and ethanol. It is observed that the maximum occupancy for σ C-O(S) and σ* C-O(S) bond orbitals is obtained for R1(O) and R3(S) 1.99338 (1.99348), 0.02224 (0.02295) in gas phase and in ethanol, respectively and 1.98245 (1.98302), 0.02668 (0.02817), in gas phase, and, in ethanol, respectively. As we explained above, small occupancies of the antibound orbitals relate, in Hartree Fock theory, to a complicated change from the idealized Lewis picture and thus to small non-covalent corrections to the picture of localized covalent bonds. The resulting p character of the corresponding sulfur natural hybrid orbital (NHO) of the σC-O(S) bond orbital is also related to the impact on molecular stability and geometry (bond lengths) of decreased occupancy of the localized σC-O(S) orbital in the idealized Lewis structure or increased occupancy of σ*C-O(S) of the non-Lewis orbital. In Table 3, for selected compounds at B3LYP level [thiol, thione, R1(S), R2(S), and R3(S)], the p characters of sulfur σ C-S values are 4.55(4.69), 4.78(4.56), 4.60(4.46), 4.55(4.46), and 4.51(4.51), in gas phase, and ethanol, respectively. Like this, the lengths of the C-S bonds are 1.787(1.784), 1.760(1.758), 1.797(1.792), 1.794(1.789), and 1.797(1.792), in gas phase, and ethanol, respectively. For [enol, keto, R1(O), R2(O) and R3(O)], the p characters of oxygen σ C-O values are 1.79(1.82), 1.00(1.61), 1.87(1.82), 3.67(3.65), and 3.76(3.74), in gas phase, and ethanol, respectively. Like this, the lengths of the C-O bonds are 1.343(1.356), 1.270(1.289), 1.361(1.366), 1.366(1.367), and 1.369(1.366), in gas phase, and ethanol, respectively. Therefore, the results indicate that the C-O(S) bond lengths of these compounds are basically controlled by the p character of these hybrid orbitals and by the nature of the C-O(S) bond.

Table 6 The important calculated valence non-Lewis and Rydberg non-Lewis, σ C-O(S) and σ*C-O(S) bond orbital occupancies in gas phase, and ethanol at B3LYP/6–311 +  + G(2d,2p).
Full size table

Natural population analysis

The natural population analysis (NPA) was evaluated using natural atomic orbital occupancies26. Table 7 in gas phase, and ethanol displays the molecular charge distribution on the skeletal atoms of the rotomeric and tautomeric forms of 2HPhAZ and 2MPhAZ. In general, it is seen that the strong negative and positive partial charges on the skeleton atoms—particularly O, N, and S—increase as the examined compounds' Hammett constants increase. The most electronegative center charges of [enol, keto, R1(O), R2(O), and R3(O)] are −0.58236(0.60716), −0.53433(−0.52220), −0.48994(−0.55563), −0.5088(−0.56684), −0.5210(−0.57059), and −0.69700(−0.74332), −0.71822(−0.83839), −0.65636 (−0.69924), −0.6867(−0.70641), and −0.6831(−0.70657), in gas phase, and ethanol respectively, which are accumulated on N and O atoms. While [thiol, thione, R1(S), R2(S), and R3(S)], the most electronegative center charges on N and S atoms are −0.60289(−0.56601), −0.5412(−0.53769), −0.5132(−0.55665), −0.5113(−0.56395), −0.5129(−0.56467), and −0.02443(−0.01982), −0.27762(−0.43861), −0.10941(−0.05444), −0.04712(−0.02862), and 0.0578(−0.02977), in gas phase, and ethanol respectively. According to the electrostatic point of view of the molecule, these electronegative atoms tend to donate electrons. Also, it is found that the most electropositive center charges of [enol, keto, R1(O), R2(O), and R3(O)] and [thiol, thione, R1(S), R2(S), and R3(S)] are accumulated on C7, C15, and C25 atoms (cf. Table 7). These electropositive atoms have a propensity to accept electrons from the perspective of the molecule's electrostatics. Table 7 lists each electronegative and electropositive atom's native electronic configuration. According to the distribution of partial charges on the skeleton atoms, electrostatic attraction or repulsion between atoms can contribute significantly to intra- and intermolecular interaction.

Table 7 Atomic charge distribution described in terms of natural population analysis (NPA) for the studied compounds in gas phase, and ethanol by using B3LYP/6–311 +  + G(2d,2p) method.
Full size table

Conclusion

Using the DFT/B3LYP/6–311 +  + G (2d, 2p) level of theory, the electronic for tautomeric and rotameric structures of 2HPhAZ and 2MPhAZ analogues is explored in gas phase, and ethanol. Enol/thiol is more stable than keto/thione form for tautomer in the statically mixed ground state in gas phase, which is considered in all computations in this article. The ethanol solvent causes some reordering of the relative stability of 2HPhAZ and 2MPhAZ conformers. For rotamer, R3(O) structure have higher stability than R2(O) and R1(O) structures, while R1(S) structure has higher stability than R3(S) and R2(S) structures. According to our findings, an intriguing aspect to note is how the bond length and angle alter as a function of the tautomeric structure's σF values. The examined compounds' increasing Hammett constants result in a rise in the p characteristics of the sulfur NHO σ C-S(O) bond orbitals. There is a strong hyperconjugated interaction between nO(S)—> σ*C25-O26(S26) and nO(S) —> σ*C15-N16 in the compounds studied. The weakness in the O(S)-C sigma bond is due to nO(S)— > σ*C25-O26(S26) and nO(S)—> σ*C15-N16 delocalization, which is responsible for the longer O(S)-C bond lengths and hence contributes to the tautomerization of 2HPhAZ and 2MPhAZ. With an increase in the examined compounds' Hammett constants, the charge transfer energy reduces. The intra- and intermolecular interactions can be significantly influenced by the electrostatic attraction or repulsion between atoms. The NBO analysis focuses on the availability of a device of high quality, shedding light on both the HB-related electron delocalization-induced hyperconjugate effects and the many effects found to influence the NH-stretch spectral shift, i.e., the main measurable quantity on which most of the spectroscopic approaches are based.