Introduction

Cancer, one of the most severe and lethal diseases, necessitates aberrant cell development that intensifies. It is a cancerous tumor with irregular cell proliferation that has the potential to attack or spread to other human body organs. For further information, check1. The rise may also be immediate, passing directly through the blood or lymphatic system. Different organs may be affected by cancer, and each type of cancer has unique traits. In relation to the location of cancers, various types of cancer are identified, including cervical cancer, lung cancer, gynecological cancer, skin cancer, brain cancer, breast cancer, etc. Breast cancer is the most common type of cancer. In recent years, the function of statistical analysis in cancer biology has grown increasingly significant in determining the various treatment alternatives. The length of time that elapses between the start of a specific time period and the occurrence of a chosen event is the subject of remission times or survival time data analysis. The purpose is usually to assess how different therapies effect remission time or survival time, and using easily available information about each patient adds to the uncertainty of the statistical distribution.

The goal of the current study is to determine how long cancer patients remain in remission after receiving EHLD. States and organizations perform tens of thousands of clinical trials annually to describe diseases and evaluate alternative therapies. The outcomes have a direct impact on how individuals are treated, thus it is critical to accurately assess the information presented in order to save both time and money. The majority of states use exploratory tools based on specified individuals to estimate the expected life or survival of patients. Acceptance sampling plans under indeterminacy would be one quality control methodology to save money and time when testing the patient's remission time or survival time. The oncologists are brainstorming to estimate the average remission time of the patients after attacked cancer due to their new method of treatment. In these situations the oncologists are paying attention to testing the null hypothesis of the average remission time of the patients is equal to the specified average remission time of the patients against the alternative hypothesis that the average remission time of the patients varies significantly. The null hypothesis could be rejected if the average remission time of the patients due to melanoma cancer, called as acceptance number of patients is greater than or equal to the specified average remission time of the patients due to melanoma cancer.

Numerous authors concentrate on studied single sampling plan (SSP) based time truncated life test for a variety of distributions. Some related article can also be explored2,3,4,5,6,7,8. More particulars related to SSP could available in9. The scheme of repetitive group acceptance sampling plan (RGASP) was first initiated by Sherman10. The improvement of single acceptance sampling plan is known as repetitive sampling plan for more details please explore11,12,13,14.

Although the aforementioned authors employed traditional statistics to examine the SSP and RASP, many real-world applications related to cancer patients' longevity may not. Recently, neutrosophic statistics have drawn the attention of more scholars in these circumstances. The development of more details about the neutrosophic logics, their quantification of determinacy, and their indeterminacy15. Various researchers considered neutrosophic logic for different real troubles and showed its competence as compared with fuzzy logic, for more information see16,17,18,19,20,21. The idea of neutrosophic statistics was given using the idea of neutrosophic logic22,23,24. Neutrosophic statistics commit information regarding the quantification of determinacy and measure of indeterminacy. Neutrosophic statistics become conventional statistics if no evidence is enrolled about the quantification of indeterminacy. The SSP using neutrosophic statistics is developed by Aslam25,26.

A fuzzy environment and the sample strategies at hand could not provide accounting data that is relevant to the measure of indeterminacy. Some works related to a single sampling plan using a fuzzy approach can also be explored27,28,29,30,31,32. More recently33,34 developed SSP and RASP to test average wind speed and COVID-19 patients for Weibull distribution under indeterminacy. When all of the observations in the sample or population are determined, the current sampling strategies based on classical statistics are employed. In practice, given the uncertainty environment, certain observations in the sample or population may be uncertain. In the latter scenario, the sampling plan for EHLD utilizing the RASP under classical statistics cannot be condemned. We were unable to identify a time-truncated sampling plan for EHLD under indeterminacy after searching the literature. We hope that the time-truncated sample strategy for EHLD under indeterminacy will be more useful for medical practitioners and industrial engineers when it comes to lot sizing in indeterminate contexts. As a result, we are motivated to examine RASP for EHLD in the presence of indeterminacy in order to calculate the average remission time. While testing to ascertain the average remission time, it is expected that the created sample design will have a lower ASN than the existing sampling designs.

In "Methodologies", we propose the RASP for EHLD under indeterminacy. A comparative study is given in "Comparative studies" and a real example based on the remission time of the patients due to melanoma cancer data is provided in "Applications of proposed plan for remission times of melanoma patients". In the end, concluding remarks, suggestions and future research works are demonstrated in "Conclusions".

Methodologies

This section's goal is to provide an overview of the EHLD using neutrosophic statistics. This section will also show how to use the RASP to study the typical length of remission for melanoma cancer patients based on uncertain circumstances.

Exponentiated half-logistic distribution under indeterminacy

We will provide a brief summary of the EHLD. The EHLD was acquainted and contemplated quite comprehensively by35, further36 studied for various acceptance sampling plans for this distribution. Suppose that \(f\left({t}_{N}\right)=f\left({t}_{L}\right)+f\left({t}_{U}\right){I}_{N};{I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\) be a neutrosophic probability density function (npdf) with determinate part \(f\left({t}_{L}\right)\), indeterminate part \(f\left({t}_{U}\right){I}_{N}\) and indeterminacy period \({I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\) for more details refer33. Remember that \({t}_{N}\epsilon \left[{t}_{L},{t}_{U}\right]\) be a neutrosophic random variable (NRV) follows the npdf. The npdf is the oversimplification of pdf under conventional statistics. The anticipated neutrosophic form of \(f\left({t}_{N}\right)\epsilon \left[f\left({t}_{L}\right),f\left({t}_{U}\right)\right]\) turns to pdf under classical statistics when \({I}_{L}\)=0. Using this background, the npdf of the EHLD is outlined as under

$$f\left({t}_{N}\right)=\left\{\left(\frac{2\theta }{\sigma }\right)\frac{{\left(1-{e}^{-\frac{{t}_{N}}{\sigma }}\right)}^{\theta -1}}{{\left(1+{e}^{-\frac{{t}_{N}}{\sigma }}\right)}^{\theta +1}}\right\}+\left\{\left(\frac{2\theta }{\sigma }\right)\frac{{\left(1-{e}^{-\frac{{t}_{N}}{\sigma }}\right)}^{\theta -1}}{{\left(1+{e}^{-\frac{{t}_{N}}{\sigma }}\right)}^{\theta +1}}\right\}{I}_{N}; {I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right],$$
(1)

where \(\sigma\) and \(\theta\) are scale and shape parameters, respectively. It is significant to note that the developed npdf of the EHLD is the oversimplification of pdf of the EHLD based on conventional statistics. The neutrosophic form of the npdf of the EHLD reduces to the EHLD when \({I}_{L}\)=0. The neutrosophic cumulative distribution function (ncdf) of the EHLD is given by

$$F\left({x}_{N}\right)=\left\{{\left(\frac{1-{e}^{-\frac{{t}_{N}}{\sigma }}}{1+{e}^{-\frac{{t}_{N}}{\sigma }}}\right)}^{\theta }\right\}+\left\{{\left(\frac{1-{e}^{-\frac{{t}_{N}}{\sigma }}}{1+{e}^{-\frac{{t}_{N}}{\sigma }}}\right)}^{\theta }\right\}{I}_{N}; {I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right].$$
(2)

The average lifetime of the NEHLD is given by

$${\mu }_{N}=\sigma \left[ln\left(\frac{1+{2}^{-1/\theta }}{1-{2}^{-1/\theta }}\right)\right]\left(1+{I}_{N}\right); {I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right].$$
(3)

Repetitive sampling plan under indeterminacy

The traditional RASP based on the truncated life test sampling scheme is initiated by37. The step-by-step procedure to adopt the repetitive acceptance sampling plan under indeterminacy is stated below:

Step 1: From a lot choose a sample of size n. Conduct a life testing for these sample for a pre-specified time say \({t}_{0}\). Indicate the average \({\mu }_{0N}\) and indeterminacy parameter \({I}_{N} \epsilon \left[{I}_{L},{I}_{U}\right]\).

Step 2: Accept \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) if specified average quantity \({\mu }_{0N}\) is less than or equal to \({c}_{1}\) (i.e., \({\mu }_{0N}\le {c}_{1}\)). If specified average quantity \({\mu }_{0N}\) is more than \({c}_{2}\) (i.e., \({\mu }_{0N}\) > \({c}_{2}\)) then we reject \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) and conclude the test, where \({c}_{1}\le {c}_{2}\).

Step 3: If \({{c}_{1}<\mu }_{0N}\le {c}_{2}\) then go to Step 1 and do again the entire procedure.

The developed RASP based on above indeterminacy methodology is consists of \(n,{c}_{1},{c}_{2}\) and \({I}_{N}\), where \({I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\) is known as uncertainty level and it is predetermined. RASP is a generalization of SSP under uncertainty studied in "Comparative studies". The proposed RASP is reduced to a SSP under uncertainty when \({c}_{1}={c}_{2}\). It is a convention to assume that \({t}_{0}=d{\mu }_{0}\) where \(d\) is the termination factor. The operating characteristic (OC) function would be obtained based on lot acceptance probability for more details refer10 and it is defined as:

$$L\left( {p_{N} } \right) = \frac{{P_{a} \left( {p_{N} } \right)}}{{P_{a} \left( {p_{N} } \right) + P_{r} \left( {p_{N} } \right)}};\quad 0 < p_{N} < 1,$$
(4)

where \(P_{a} \left( {p_{N} } \right)\) is the chance of accepting under \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) whereas \(P_{r} \left( {p_{N} } \right)\) is the chance of rejecting at \({H}_{0}:{\mu }_{N}={\mu }_{0N}\), these are obtained in the following expressions:

$$P_{a} \left( {p_{N} } \right) = \sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{N}^{i} \left( {1 - p_{N} } \right)^{n - i} ,$$
(5)
$${\text{and}}\quad P_{r} \left( {p_{N} } \right) = 1 - \sum\limits_{i = 0}^{{c_{2} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{N}^{i} \left( {1 - p_{N} } \right)^{n - i} ,$$
(6)

where \(p_{N}\) is the chance of rejecting \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) and it is obtained from Eq. (2) and Eq. (3) and it is defined by

$${p}_{N}=\left\{{\left(\frac{1-\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}{1+\mathrm{exp}\left(-\frac{\mathrm{d\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}\right)}^{\theta }\right\}+\left\{{\left(\frac{1-\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}{1+\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}\right)}^{\theta }\right\}{I}_{N}.$$
(7)

Where \(\vartheta =ln\left(\frac{1+{2}^{-1/\theta }}{1-{2}^{-1/\theta }}\right)\).

Using Eqs. (5) and (6) the Eq. (4) becomes

$$L\left( {p_{N} } \right) = \frac{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{N}^{i} \left( {1 - p_{N} } \right)^{n - i} }}{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{N}^{i} \left( {1 - p_{N} } \right)^{n - i} + 1 - \sum\limits_{i = 0}^{{c_{2} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{N}^{i} \left( {1 - p_{N} } \right)^{n - i} }};\quad 0 < p_{N} < 1.$$
(8)

The researcher is paying attention to concern the developed scheme to test \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) such that the chance of accepting \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) while it is true ought to be more than \(1-\alpha\) (\(\alpha\) is type-I ) for \(\mu /{\mu }_{0}\) and the chance of accepting \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) while it is wrong ought to be smaller than \(\beta\) (type-II error) for \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}=1\). In producer opinion, the chance of approval should be greater than or equal to \(1-\alpha\) at acceptable quality level (AQL), \(p_{1N}\). In the same way, in consumer opinion the lot rejection chance ought to be less than or equal to \(\beta\) at limiting quality level (LQL),\(p_{2N}\). The intended quantities would be obtained by solving the following two inequalities simultaneously.

$$L\left( {p_{1N} \left| {{{\mu_{N} } \mathord{\left/ {\vphantom {{\mu_{N} } {\mu_{0N} }}} \right. \kern-0pt} {\mu_{0N} }}} \right.} \right) = \frac{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{1N}^{i} \left( {1 - p_{1N} } \right)^{n - i} }}{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{1N}^{i} \left( {1 - p_{1N} } \right)^{n - i} + 1 - \sum\limits_{i = 0}^{{c_{2} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{1N}^{i} \left( {1 - p_{1N} } \right)^{n - i} }} \ge 1 - \alpha ,$$
(9)
$$L\left( {p_{2N} \left| {{{\mu_{N} } \mathord{\left/ {\vphantom {{\mu_{N} } {\mu_{0N} = 1}}} \right. \kern-0pt} {\mu_{0N} = 1}}} \right.} \right) = \frac{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{2N}^{i} \left( {1 - p_{2N} } \right)^{n - i} }}{{\sum\limits_{i = 0}^{{c_{1} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{2N}^{i} \left( {1 - p_{2N} } \right)^{n - i} + 1 - \sum\limits_{i = 0}^{{c_{2} }} {\left( \begin{gathered} n \hfill \\ i \hfill \\ \end{gathered} \right)} p_{2N}^{i} \left( {1 - p_{2N} } \right)^{n - i} }} \le \beta .$$
(10)

where \({p}_{1N}\) and \({p}_{2N}\) are respectively given by

$${p}_{1N}=\left\{{\left(\frac{1-\mathrm{exp}\left(-{{\rm d}\vartheta }\left(1+{I}_{N}\right)\right)}{1+\mathrm{exp}\left(-{{\rm d}\vartheta }\left(1+{I}_{N}\right)\right)}\right)}^{\theta }\right\}+\left\{{\left(\frac{1-\mathrm{exp}\left(-{{\rm d}\vartheta }\left(1+{I}_{N}\right)\right)}{1+\mathrm{exp}\left(-{{\rm d}\vartheta }\left(1+{I}_{N}\right)\right)}\right)}^{\theta }\right\}{I}_{N},$$
(11)

and

$${p}_{2N}=\left\{{\left(\frac{1-\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}{1+\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}\right)}^{\theta }\right\}+\left\{{\left(\frac{1-\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}{1+\mathrm{exp}\left(-\frac{{{\rm d}\vartheta }\left(1+{I}_{N}\right)}{{\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}}\right)}\right)}^{\theta }\right\}{I}_{N}.$$
(12)

The estimated intended quantities of the developed scheme should be minimizing the average sample number (ASN) at AQL. The ASN of the developed sampling scheme in terms of fraction defective (\(p_{N}\)) is given below:

$$ASN = \frac{n}{{P_{a} \left( {p_{N} } \right) + P_{r} \left( {p_{N} } \right)}} .$$
(13)

The intended quantities for the created method would therefore be determined by resolving the nonlinear programming problem for optimization shown below.

$$\begin{gathered} {\text{Minimize }}ASN(p_{1N} ) \hfill \\ {\text{subject to }} \hfill \\ L\left( {p_{1N} } \right) \ge 1 - \alpha \hfill \\ L\left( {p_{2N} } \right) \le \beta \hfill \\ 0 \le c_{1} \le c_{2} \hfill \\ {\text{where }}n,c_{1} ,c_{2} \in z. \hfill \\ \end{gathered}$$
(14)

The values of the intended quantities \(\left\{n,{c}_{1}, {c}_{2}\right\}\) for various values of \(\beta\) = {0.25, 0.10, 0.05}; \(\alpha =0.10\); \(d=\left\{0.5, 1.0\right\}\), \({\mu }_{N}/{\mu }_{0N}\)={1.2, 1.3, 1.4, 1.5, 1.8, 2.0} and \({I}_{N}\)= {0.0, 0.02, 0.04, 0.05} for shape parameter \(\theta =\left\{{1,5}, 2.0, 1.0\right\}\) are presented in Tables 1, 2, 3, 4, 5 and 6. Tables 1 and 2 are shown for the EHLD for \(\theta =1.5\), Tables 3 and 4 for \(\theta =2.0\), Tables 5 and 6 for \(\theta =1\) (half-logistic distribution). From these tables, we pointed out the below few points.

  1. a.

    When the values of \(d\) increases from 0.5 to 1.0 the value of \(ASN\) decreases.

  2. b.

    It is pointed out that if the shape parameter increases from \(\theta =1 to \theta =2\) the values of \(ASN\) decreases when other parameters are fixed.

  3. c.

    Further, it is observed that the indeterminacy value \({I}_{N}\) also showing a considerable effect to derogating the \(ASN\).

Table 1 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.5\) and \(d=0.50\).
Full size table
Table 2 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.5\) and \(d=1.00\).
Full size table
Table 3 The RASP parameter of EHLD when \(\alpha =0.10;\theta =2.0\) and \(d=0.50\).
Full size table
Table 4 The RASP parameter of EHLD when \(\alpha =0.10;\theta =2.0\) and \(d=1.00\).
Full size table
Table 5 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.0\) and \(d=0.50\).
Full size table
Table 6 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.0\) and \(d=1.00\).
Full size table

Comparative studies

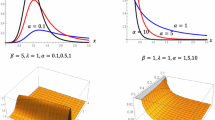
This section's goal is to examine the projected RASP's effectiveness in relation to ASN. The average hypothesis may be examined more affordably the lower the ASN. If no uncertainty or indeterminacy is established while remembering the average value, note that the sampling plan developed is an oversimplification of the plan based on conventional statistics. When \({I}_{N}\)=0, the developed RSP becomes the on-hand sampling plan. In Tables 1, 2, 3, 4, 5 and 6 the first spell of column i.e. at \({I}_{N }\)= 0 is the plan parameter of the traditional or existing RASP. From the results from the tables, we would conclude that the ASN is large in traditional RASP as compared with the proposed RASP. For example, when \(\alpha =0.10, \beta =0.25,\) \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}\)=1.3, \(\theta\)=1.5 and \(d\)=0.5 from Table 1, it can be seen that \(ASN\)=107.11 from the plan under classical statistics and \(ASN\)=95.82 for the projected RASP when \({I}_{N}\) = 0.05. Furthermore, when \(\theta\)=1 the EHLD becomes a half-logistic distribution (HLD), we have constructed Tables 5 and 6 for half-logistic distribution for comparison purpose. Table 5 depicts that EHLD shows less ASN as compared with HLD. For example when \(\alpha =0.10,\beta =0.10,\) \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}\)= 1.5, \(d\)= 0.5 and \({I}_{N}\)= 0.04 the Table 5 shows that the ASN is 100.99 where as proposed plan values are ASN = 67.83 for \(\theta\) = 1.5 and ASN = 51.76 for \(\theta\) = 2.0. From this study, it is concluded that the projected plan under indeterminacy is efficient over the existing RASP under traditional statistics with respect to sample size. We have also compared our proposed RASP under indeterminacy with SSP under indeterminacy developed by38. The results show that RASP is superior to the SSP for same specific parameters. For example when \(\alpha =0.10,\beta =0.10,\) \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}\) = 1.4, \(d\)= 0.5, \({I}_{N }\)= 0.04 and \(\theta\) = 1.5 the ASN in SSP is 105 whereas in RASP the ASN is 67.83. Operating characteristic (OC) curve of plan of the EHLD when \(\alpha =0.10, \beta =0.10,\theta =2\), \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}\)= 1.3 and \(d\) = 0.5 is depicted in Fig. 1. From Fig. 1, we conclude that indeterminacy parameter shows significant effect on reduce the ASN. Therefore, the application of the proposed plan for testing the null hypothesis \({H}_{0}:{\mu }_{N}={\mu }_{0N}\) demands a lesser ASN as compared to the on hand plan. Moreover, the OC curve comparison between SSP and RASP is also displayed in Fig. 2. The OC curve in Fig. 2 also shows that RASP is superior to the SSP for the same specific parameters. The researchers advised as proposed RASP under uncertainty is more economical to apply in a medical study specifically for remission time of the patients due to melanoma cancer.

Figure 1
figure 1

OC curve plan at different indeterminacy values.

Full size image
Figure 2
figure 2

OC curves comparison between SSP and RASP under indeterminacy.

Full size image

Applications of proposed plan for remission times of melanoma patients

The present section deals with the postulation of the developed sampling scheme for the EHLD under the indeterminacy obtained by means of a real paradigm. This data set is picked out from39 and it constitutes the remission times, in months for 30 melanoma cancer patients at stages 2 to 4. For ready reference, the data is given below.

Remission time (months): 33.7, 3.9, 10.5, 5.4, 19.5, 23.8, 7.9, 16.9, 16.6, 33.7, 17.1, 8.0, 26.9, 21.4, 18.1, 16.0, 6.9, 11.0, 24.8, 23.0, 8.3, 10.8, 12.2, 12.5, 24.4, 7.7, 14.8, 8.2, 8.2 and 7.8.

Melanoma is a very dangerous kind of skin cancer which develops in the cells (melanocytes) that develop melanin and it creates the color change in the skin.

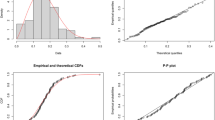
It is establish that the remission times of melanoma patients data comes from the EHLD with shape parameter \(\widehat{\theta }=\) 1.4097 and scale parameter \(\widehat{\sigma }=7.3811\) and the maximum distance between the real time data and the fitted of EHLD is found from the Kolmogorov–Smirnov test as 0.1324 and also the p-value is 0.6687. The demonstration of the goodness of fit for the given model is shown in Fig. 3, the empirical and theoretical cdfs and Q-Q plots for the EHLD for the remission times of melanoma patients’ data. In Tables 7 and 8 presented the plan quantities for the fitted shape parameter. It is assumed there is indeterminacy in measuring remission time and let it is 0.05. The measurements of remission time for cancer patients with respect to interval measures and fuzzy-type data sets were studied by various authors, for instance, refer40,41,42. For the proposed plan, the shape parameter is \({\widehat{\theta }}_{N}=(1+0.05)\times 1.4097 \approx 1.4802\) when \({I}_{U}\) = 0.05. Assume that a medical researcher would like to employ the developed RSP for EHLD under indeterminacy to guarantee the remission time of melanoma cancer patients is at least 6 months using the truncated life test for 3 months (thus d = 0.5). Suppose that medical researchers are paying attention to test \({H}_{0}:{\mu }_{N}=4.7893\) with the support of the developed RASP when \({I}_{U}\) = 0.05,\(\alpha =0.10\), \({\upmu }_{{\rm N}}/{\upmu }_{0{\rm N}}\)= 1.5, \(d\) = 0.5 and \(\beta\) = 0.10. From Table 7, it can be noted that n = 40, \({c}_{1}\)= 5, \({c}_{2}\)= 9 and ASN = 68.35. Thus, the RASP for EHLD under indeterminacy could be enforced in the following way: picking out a random sample of 40 melanoma cancer patients from the indoor group of patients, and conducting the truncated life test of remission time for 3 months. The developed RASP scheme could be adopted in the following way: hypothesis \({H}_{0}:{\mu }_{N}=4.7893\) will be accepted if the average remission time of melanoma cancer patients in 6 months is less than five patients, but a lot of patients should be rejected as soon as the remission time of melanoma cancer patients exceeds nine patients. Contrary, the experimentation could be repeated. From remission time data shows that seven patients before the average remission time of melanoma cancer patients of 4.7893. Therefore, the medical practitioners would have to repeat the entire procedure until accept/reject the hypothesis. Accordingly, it is competent that the developed sampling will be taken into consideration to check the typical length of remission for melanoma cancer patients based on the real application.

Figure 3
figure 3

The empirical and theoretical pdf and Q-Q plots for the EHLD for the remission times of melanoma patients.

Full size image
Table 7 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.4097\) and \(d=0.50\).
Full size table
Table 8 The RASP parameter of EHLD when \(\alpha =0.10;\theta =1.4097\) and \(d=1.00\).
Full size table

Conclusions

In order to design an exponentiated half-logistic distribution based on indeterminacy for a time-truncated repetitive sampling strategy, a thorough investigation of melanoma cancer patients was conducted. The sample scheme parameters are determined for the identified values of the indeterminacy parameters. For simple reference, we have given lengthy tables including the values of the known indeterminacy constants. The developed sampling strategy is compared to the available conventional statistical strategies. The results show that the designed sampling plan is more cost-effective than the on-hand SSP under indeterminacy and conventional sampling plans. Furthermore, the proposed RASP under indeterminacy is more cost effective than the single sample strategy. It is also noticed that indeterminacy values play a vital role in ASN, when the indeterminacy quantities increase at that time the ASN quantity is decreased. Hence, the proposed sample strategies are convenient for researchers, particularly in medical experimentation, because medical experimentation requires more costly and qualified specialists. As a result, the created sampling strategy under indeterminacy is required to be valid for testing the average number of melanoma cancer patients. The real examples based on the melanoma cancer patients for developed sampling scheme under indeterminacy show a piece of evidence. The suggested sampling strategy for big data analytics could be applied to various scientific and technical disciplines. The next step in the research would be to develop multiple dependent state sampling plans and multiple dependent state repeating sampling plans for different lifetime distributions.