Abstract
This study is carried out to analyze the problem of mixed convection magnet nanoflow of Prandtl fluid through a non-uniform channel with peristalsis. The external influences of activation energy and non-constant velocity slip are given full consideration. The mentioned fluid is expressed as a governing equations system, and then these equations are converted with non-dimensional parameter values to a system of ordinary differential equations. The converted system of equations is solved in terms of y and then graphs and sketches are offered using the generalized differential transform method. Graphs and results for volume friction as well as velocity profile, concentration, and temperature distributions are obtained. Results show development in the velocity profile of fluid distribution through high values of the non-constant velocity slip effect. The present study is alleged to deliver more opportunities to advance the applications of the drug-carrying system in hypoxic tumor areas with aid of identifying the flow mechanisms.
Similar content being viewed by others
Introduction
Lately, the important applications of non-Newtonian fluids in diverse fields have prompted investigators to study these kinds of fluids. Thus, the impact of thermal radiation on MHD Maxwell nanofluid is reported by Mahmood et al.1. They noticed that the rise in the temperature-dependent thermal conductivity parameter leads to elevate nanofluid temperature. Reddy and Makinde2 introduce a new analytical study of buoyancy forces on the influx of non-Newtonian fluids. In their investigation, they found that the volume fraction boosts with an enhancement in thermophoresis parameter \(Nt\). As well, researchers, focus their concern on studying the implementations of non-Newtonian fluids in the existence of nanoparticles. Such as oil refinement implementations3,4, implementations of physiological systems5, biomedical applications6, drug delivery systems7,8, rheumatoid arthritis9, and digestive system10. Prandtl fluid is deemed an important kind of non-Newtonian fluid. It’s known as a pseudo-plastic visco-inelastic non–Newtonian fluid. Therefore, several studies included this kind of fluid. So, Akram et al.11 analyzed the hybrid influences of magnetic field and thermal convection on Prandtl nanofluid. In their illustration study, they observed that the velocity dwindles when \(y \in \left[ {0, 0.3} \right]\) whilst, it escalates when \({\text{y}} \in \left[ {0.3,{ }1.2} \right].\) Over and above, many other analytical studies discuss the diverse applications of non-Newtonian nanofluids12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39.
Energy has an indispensable significant role in several implementations, like physical, engineering, and chemical areas. Thus, it has attracted the interest of investigators. In general, activation energy is the energy that must be applied to a chemical or nuclear system of latent reactants leading to a chemical reaction, or other physical phenomena. Moreover, in 1889, the term was coined by Arrhenius40. Shafique et al.41 discussed the boundary flow containing a rotating frame in the existence of activation energy. In their discussion, they observed that the activation energy is an increasing function in the fluid temperature. Gowda et al.42 studied a velocity distribution for the boundary layer influx in the existence of activation energy impact. Several studies include various implementations of this significant energy43,44,45,46,47,48.
The slip velocity is known as the difference in velocities between liquids in the vertical inflow of two-phase combinations through a pipe. Over and above, slip velocity in heart valves comes on top of its validation49. Nisar et al.50 analyzed the influences of both slip and activation energy on the peristaltic influx of Eyring Powell nanofluid. They observed that the velocity escalates with an enrichment in the slip parameter. Akbar and Nadeem51 propose a new model for Jeffrey’s fluid in the existence of slip impacts. They noticed in their study that the pressure rise elevates with an enhancement in the slip parameter. The slip velocity is considered in some studies because of its importance in artificial heart valves. Supplementary, see1,6,10,26,27,28. In the current study, the variable slip velocity is studied to assure its significant role in heart valves49,50.
Solutions to the diverse systems of equations are introduced with divergent classical techniques that are not convenient for innovation in this study. Whilst, a credible procedure utilized to solve the highly non-linear system of ordinary differential equations is named the generalized differential transform method (GDTM)52. This method proved to be effective in treating several kinds of equations. Also, the approximate solutions can be obtained with an error rate of up to \(10^{ - 10}\) when this semi-analytical method is applied53, and divergent in GDTM has been appropriately contained. This current analytical study displayed a new generalization to the differential transform method to get a better solution to Prandtl nanofluid model. Several researchers studied this method, see54,55.
The novelty of this study is to illustrate the impacts of variable velocity slip and activation energy on MHD Prandtl nanofluid. The fluid inflows through a non-uniform channel. Distributions of velocity, temperature, concentration, and nanoparticle volume fraction are obtained by GDTM. Solutions/results are obtained without any perturbation/restrictive suggestion using GDTM. In the present paper, we construct the main results; both the nanoparticle’s volume friction \({\Omega }\) and the concentration \(\varphi\) have an opposite behavior compared to the temperature behavior except that they increase or decrease with the increase of Sc. Physically, our model corresponds to the transport of the gastric juice in the small intestine when an endoscope is inserted through it. The formulation of the problem is introduced in "Formulation problem" section: the method of solution for the resultant system of equations is presented in "Method of solution" section. Numerical discussion and analysis of results are discussed in "Results and discussion" section. In "Conclusion" section involves the essential summarized remarks of this study.
Formulation problem
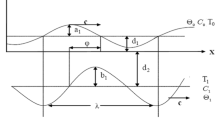
Incompressible two-dimensional MHD peristaltic flow of Prandtl nanofluid in a non-uniform channel is deliberated. The fluid velocity c in the \(x - axis\) coordinates, with a width \(b\). The induced magnetic field is neglected while the uniform magnetic field is applied with strength \(B_{0}\) perpendicular to \(x - axis\) see Fig. 1.
\(A_{1} \left( {\hat{x}} \right) = A_{0} + \overline{m}\hat{x}\), where \(A_{1} \left( {\hat{x}} \right), A_{0} , \hat{x}, b, \hat{t}, c,\lambda \;{\text{and}}\;m\) are the width of the channel, the value of half-width at the inlet, the axial space, the amplitude wave, the time, the velocity of propagating wave, the wavelength, the non-uniform parameter, respectively. Indeed, at \(m = 0\) the channel wall will be a uniform channel. In two-dimensional, the axial velocity of flow is \(\hat{V} = \left[ {\hat{U}\left( {\hat{X}, \hat{Y},\widehat{ t}} \right), \hat{V}\left( {\hat{X}, \hat{Y},\widehat{ t}} \right), 0} \right].\)
The Prandtl fluid is offered as in11,12,13:
where \(A\) and \(B\) are the constants of the Prandtl fluid tensor.
Rosseland’s approximation is designated as:
The equations of motion of incompressible flow in a two-dimensional laboratory frame \(\left( {\hat{X}, \hat{Y}} \right)\) are as follows:
Here \(f,g, \beta_{{\hat{C}}} , \beta_{{\hat{T}}} ,\rho_{f} ,\hat{\user2{S}}, \hat{T}, \hat{C},\rho_{p} , \hat{\Upsilon }, D_{B} ,\rho_{f0} , D_{{\hat{T}}} ,\left( {\rho c} \right)_{p} , D_{{\hat{C}\hat{T}}} , D_{s} , \left( {\rho c} \right)_{f} ,D_{{\hat{T}\hat{C}}} ,\; {\text{and }}\frac{d}{dt}\) are the body force, the acceleration due to gravity, the fluid volumetric solutal expansion, the fluid volumetrically thermal expansion, fluid heat capacity, the stress tensor of Prandtl fluid, the flow temperature, concentration and nanoparticle volume fraction, the base fluid density, the fluid density at \(T_{0}\), the nanoparticle heat capacity, the density of the particles respectively, the Brownian diffusion, the thermophoresis diffusion, the sort diffusively, the solutal diffusively, DuFour diffusively, the material time derivative, respectively.
As we recognize, \(\left( {X, Y} \right)\) describes the unsteady flow in a fixed frame, but \(\left( {x, y} \right)\) refers to the steady wave frame motion. The non-dimensional relation between the wave and fixed frame is as follows:
Levy the dimensionless parameters as follows:
\(\hat{x} = \frac{x}{\lambda },\hat{y} = \frac{y}{{b_{0} }}, \hat{t} = \frac{ct}{\lambda }, \hat{v} = \frac{v}{c}, u = \frac{\partial \psi }{{\partial y}}, v = - \delta \frac{\partial \psi }{{\partial x}}, \delta = \frac{{b_{0} }}{\lambda }\) is the wave number, \(\hat{p} = P\frac{{b_{0}^{2} }}{\mu c\lambda }\) is the pressure, \(Re = \frac{{c\rho_{f} b_{0} }}{\mu }\) is the Reynolds number, \({\Omega } = \frac{{\hat{\Upsilon } - \hat{\Upsilon }_{0} }}{{\hat{\Upsilon }_{1} - \hat{\Upsilon }_{0} }}\) is the nanoparticle fraction, \(\theta = \frac{{\hat{T} - \hat{T}_{0} }}{{\hat{T}_{1} - \hat{T}_{0} }}{ }\) is the temperature, \(\varphi = \frac{{\hat{C} - \hat{C}_{0} }}{{\hat{C}_{1} - \hat{C}_{0} }}\) is the concentration, \(P_{r} = \frac{{\left( {\rho c} \right)_{f} \nu }}{{\kappa_{0} }}\) is Prandtl number, \(Le = \frac{\nu }{{D_{s} }}\) is the Lewis number, \(S_{c} = \frac{{\left( {\hat{T}_{1} - \hat{T}_{0} } \right)D_{{\hat{C}\hat{T}}} }}{{D_{s} \left( {\hat{C}_{1} - \hat{C}_{0} } \right)}}\) is the Dufour parameters, \(S_{r} = \frac{{\left( {\hat{C}_{1} - \hat{C}_{0} } \right)D_{{\hat{T}\hat{C}}} }}{{\left( {\hat{T}_{1} - \hat{T}_{0} } \right)\varsigma }}{ }\) is the Soret parameter, \(M = \sqrt {\frac{\sigma }{\mu }} b_{0} B_{0}\) is the Hartmann number \(G_{r} = \frac{{gb_{0}^{2} \left( {1 - \hat{\Upsilon }} \right)\rho_{f} \beta_{{\hat{T}}} \left( {\hat{T}_{1} - \hat{T}_{0} } \right)}}{{\mu_{0} c}}\) is the thermal Grashof numbers, \(G_{c} = \frac{{gb_{0}^{2} \left( {1 - \hat{\Upsilon }} \right)\rho_{f} \beta_{{\hat{C}}} \left( {\hat{C}_{1} - \hat{C}_{0} } \right)}}{{\mu_{0} c}}\) is the nanoparticle Grashof numbers, \(G_{F} = \frac{{gb_{0}^{2} \left( {\rho_{p} - \rho_{f} } \right)b_{0}^{2} \left( {\hat{\Upsilon }_{1} - \hat{\Upsilon }_{0} } \right)}}{{\mu_{0} c}}\) is the solutal Grashof numbers, \(Ln = \frac{\nu }{{D_{B} }}{ }\) is the nanofluid Lewis number, \(N_{t} = \frac{{\left( {\rho c} \right)_{p} D_{T} \left( {{\hat{\text{T}}}_{1} - {\hat{\text{T}}}_{0} } \right)}}{{\hat{T}_{0} \varsigma }}\) is the thermophoresis parameters and \(N_{b} = \frac{{\left( {\rho c} \right)_{p} D_{B} \left( {\hat{\Upsilon }_{1} - \hat{\Upsilon }_{0} } \right)}}{\varsigma }\) is the Brownian motion parameter, \(R = \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{T_{0}^{3} }}{{\varsigma c_{f} }}\) is the thermal radiation parameter, \(B_{r} = E_{c} {\text{Eckret number}} \times P_{r}\).
After dropping pars, using the long wavelength and low Reynolds number, dimensionless parameters, Eqs. (4)–(9) in wave frame becomes:
Eliminate pressure from Eqs. (13) and (14) yields
Here, the tensor of the present non-Newtonian fluid (Prandtl fluid) is as follows:
\(\sigma = \frac{A}{\mu B}, {\text{and }}\beta_{1} = \frac{{\alpha_{1} c^{2} }}{{B^{2} b_{0} }}\) are the parameters of Prandtl fluid.
Therefore non-constant velocity slip is occupied to sightsee the performance of mucus and secretion of layers. The velocity restraints are clear as4:
In which \(U_{w}^{^{\prime}}\) portrays the wall velocity, \(s_{xy}\) stress tensor mechanisms, \(\xi\) non-constant velocity slip parameter. No slip constraints are taken by \(\xi = 0\).
Method of solution
The fluid model of the high non-linear differential Eqs. (12–15) nominated overhead is converted with GDTM as in52,53,54,55, and then the recurrence relations can gain the series solutions of velocity, temperature, concentration, and volume fraction solutions. Accordingly, results/graphs are calculated for distributions of flow velocity, temperature, concentration, and nanoparticle fraction versus different values of a physical parameter of interest:
Let,
Subject to the initial equations
The function \(f\left( t \right)\) is expressed by a finite series and can be written as:
The GDTM series solution for a system ((12–15)) can be obtained as,
Now, the skin friction coefficient τω, the heat transfer coefficient (Nusselt number) Nu and the mass transfer coefficient (Sherwood number) Sh at the wavy wall of the outer tube, are defined, respectively, by
The expressions for τω, Nu and Sh have been obtained by substituting from Eqs. (24)–(26) into Eq. (28) respectively, and they have been evaluated numerically for several values of the parameters of the problem, using the software Mathematica package. The obtained results will be discussed in the next section.
Results and discussion
In this section, the computational results are evaluated for this problem by using the Wolfram MATHEMATICA package ver. 13.1.1. The next values of humans small intestine parameters are utilized30
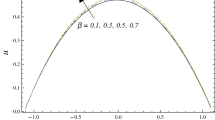
Based on Eq. (27), Figs. 2 and 3 elucidate the non-material parameter \(\beta_{1}\) influence and the parameter of non-constant velocity slip \(\xi\) on the axial velocity u, respectively. It is appreciated from Figs. 2 and 3, that the axial velocity upturns as \(\beta_{1}\) rises, while it declines as \(\xi\) growths in the interval \(y \in { }\)[0, 0.6]. otherwise, it rises by snowballing \(\xi\) and declines as \(\beta_{1}\) grows. So, the performance of u in the interval \(\eta\) ∈ [0, 0.6], is in contradictory manner of its behavior in the interval \(\eta\) ∈ [0.6, 1.2]. It is also noted that the axial velocity for small values of \(\beta_{1}\) and large values of \(\xi\) increases by increasing y to a maximum value (to a critical point of \({\text{y}}:{\text{y }} = {\text{y}}_{0}\)) subsequently, it declines. The effects of \(\beta\) and \(\sigma\) on u are found to be similar to the effects of \(\beta_{1}\) in Fig. 2. Moreover, Fig. 3 depicts that the non-constant slip parameter has a dual role in phenomena on the velocity distribution. As per the newton’s law of viscosity, velocity distribution is considered a cumulative function in shear stress. The impact of divergent-convergent parameter m on the velocity profile u as a dimensionless coordinate function of \(y\) is shown in Fig. 4. It is found that the axial velocity declines by aggregate values of m. Also, the result in Fig. 3 agrees with those obtained by29.
Figures 5 and 6 offer the influences of the thermophoresis parameter Nt and the non-constant slip velocity parameter \(\xi\) on the temperature profile against the transverse coordinate y, respectively. It is observed that the temperature increases by increasing Nt, whereas it decreases by increasing values of \(\xi\). Also, the distribution of temperature the profile is continue optimistic and negative for little values of \({\text{Nt}}\) and great values of \(\xi\), there is a semi-linear relation between the axial velocity and the dimensionless coordinate y. The result in Fig. 5 shows that the improving values of thermophoresis get the nanoparticle-enhanced temperature. Both the sinusoidal layer thickness and nanoparticles concentration boundary thickness are enhanced through this result.
The lowest amount of energy that allows a chemical reaction to occur is mentioned by activation energy. The effects of both activation energy parameter \(E_{a}\) and non-uniform parameter m on the concentration distribution \(\varphi\) as a function of the radial coordinate y is shown in Figs. 7 and 8, respectively. It is found that the concentration distribution increases by increasing \(E_{a}\) and it decreases as m increases. Figure 9 illustrates the behavior of the concentration distribution \(\varphi\) with the radial coordinate y for various values of Schmidt number Sc. It is obvious that in the interval y \(\in\)[0, 0.84]; the concentration distribution increases by increasing Sc, otherwise it decreases by increasing Sc. So, the performance of f in the interval y \(\in\)[0, 0.84], is contradictory manner of its performance in the interval y \(\in\)[0.84, 1.2] except that the curves are night boor hood to respectively other in the second interval, called, straight the channel boundary, then those acquired in the first interval. The influences of \(G_{F}\) and \(\sigma\) on the concentration are found to be parallel to the influence of m given in Fig. 8, but figures are excluded here to save space.
The variance of the nanoparticles volume friction \({\Omega }\) versus y for distinct values of and the variable velocity slip parameter \(\xi\) and the non-material parameter \(\beta_{1}\) is portrayed in Figs. 10 and 11, respectively. It is observed that the volume fraction of nanoparticles amplify with the growth in the value of \(\xi\), while it decreases as \(\beta_{1}\) increases.
Contour lines distribution are graphed versus different numbers of (\(M\)), and (\(\beta_{1}\)) by Figs. 12 and 13. Figure 12 elucidates that the number of bolus/trapped zones growths with at high numbers of \(M\), It’s portrayed from Fig. 13 that the behavior of the circulating bolus shrinkages under the result of high numbers of \(\beta_{1}\). Physically, the fluid particles become more free in boluses through ejaculation, the number of trapped bolus growth bases the velocity of fluid upturns.
Table 1 presents numerical results for the skin friction coefficient \(\tau_{\omega }\), Nusselt number Nu and Sherwood number Sh for various values of Prandtl number Pr and the parameters of Prandtl fluid \(\beta_{1}\). It is clear from Table 1 that an increase in Pr increases the values of both τxy and Nu, while Sh decreases. Furthermore, an increase in \(\beta_{1}\) gives an opposite behavior to Pr. Moreover, the result in Table 1 are in agreement with those obtained by46.
Conclusion
In the present study, a non-constant slip velocity effect on magneto Nano peristaltic flow of Prandtl fluid with heat and mass transfer in a non-uniform channel with sinusoidal deformation is treated semi-numerically. External influences like radiation, Ohmic heat, and viscous dissipation are considered. The fluid equations converted with non-dimensional values to a system of ordinary system of differential equations ODEs. The converted system of equations is solved in terms of \(y\) and then graphs/sketches are offered using GDTM. The present analysis can serve as a model which may help in understanding the mechanics of physiological flows20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39. The numerical results indicate the following:
-
(1)
The axial velocity u rises or declines with the growth each of \(\beta_{1}\), \(\xi\), Nt, and Da, whereas it declines as m growths.
-
(2)
The axial velocity w for small values of \(\beta_{1}\), \(\xi\), Nt, becomes larger with growing the radial coordinate y and reaches the maximum value (at a finite value of y: y = y0) after which it declines.
-
(3)
The temperature \(\theta\) advances in high values of \(\beta_{1}\), Nt, and \(\sigma\) parameters however it attenuations as both \(\xi\) and m grow.
-
(4)
Solutions/results are obtained without any perturbation/restrictive suggestion using GDTM.
-
(5)
Both the nanoparticle’s volume friction \({\Omega }\) and the concentration \(\varphi\) have an opposite behavior compared to the temperature behavior except that they increase or decrease with the increase of Sc.
-
(6)
In future work, the influences of emerging parameters on the pressure drop across the channel will be improved in the next paper.
Data availability
The datasets generated and/or analyzed during the current study are not publicly available due to [All the required data are only with the corresponding author] but are available from the corresponding author on reasonable request.
References
Mahmood, A., Aziz, A., Jamshed, W. & Hussain, S. Mathematical model for thermal solar collectors by using magnetohydrodynamic Maxwell nanofluid with slip conditions, thermal radiation, and variable thermal conductivity. Results Phys. 7, 3425–3433 (2017).
Gnaneswara Reddy, M. & Makinde, O. D. Magnetohydrodynamic peristaltic transport of Jeffrey nanofluid in an asymmetric channel. J. Mol. Liq. 223, 1242–1248 (2016).
Hasona, W. M., El-Shekhipy, A. A. & Ibrahim, M. G. Combined effects of magnetohydrodynamic and temperature dependent viscosity on peristaltic flow of Jeffrey nanofluid through a porous medium: Application to oil refinement. Int. J. Heat Mass Transf. 126, 700–714 (2018).
El Ouaf, M. & Abou-zeid, M. Y. Hall currents effect on squeezing flow of non- Newtonian nanofluid through a porous medium between two parallel plates. Case Studies in Thermal Engineering 28, 101362 (2021).
Eldabe, N. T. M., Abou-zeid, M. Y., Mohamed, M. A. A. & Abd-Elmoneim, M. M. MHD peristaltic flow of non-Newtonian power-law nanofluid through a non-Darcy porous medium inside a non-uniform inclined channel. Arch. Appl. Mech. 91, 1067–1077 (2021).
Abou-zeid, M. Y. Implicit homotopy perturbation method for MHD non-Newtonian nanofluid flow with Cattaneo–Christov heat flux due to parallel rotating disks. J. Nanofluids 8(8), 1648–1653 (2019).
Eldabe, N. T., Moatimid, G. M., Abouzeid, M. Y., ElShekhipy, A. A. & Abdallah, N. F. A semianalytical technique for MHD peristalsis of pseudoplastic nanofluid with temperature- dependent viscosity: Application in drug delivery system. Heat Transf. Asian Res. 49, 424–440 (2020).
Eldabe, N. T. M., Rizkallah, R. R., Abou-zeid, M. Y. & Ayad, V. M. Thermal diffusion and diffusion thermo effects of Eyring–Powell nanofluid flow with gyrotactic microorganisms through the boundary layer. Heat Transf. Asian Res. 49, 383–405 (2020).
Ibrahim, M. G., Hasona, W. M. & ElShekhipy, A. A. Concentration-dependent viscosity and thermal radiation effects on MHD peristaltic motion of Synovial Nanofluid: Applications to rheumatoid arthritis treatment. Comput. Methods Programs Biomed. 170, 39–52 (2019).
Eldabe, N. T. M., Rizkallah, R. R., Abou-zeid, M. Y. & Ayad, V. M. Effect of induced magnetic field on non-Newtonian nanofluid Al2O3 motion through boundary-layer with gyrotactic microorganisms. Therm. Sci. 26, 411–422 (2022).
Akram, S., Athar, M. & Saeed, K. Hybrid impact of thermal and concentration convection on peristaltic pumping of Prandtl nanofluids in non-uniform inclined channel and magnetic field. Case Stud. Therm. Eng. 25, 100965 (2021).
Abou-zeid, M. Y. Homotopy perturbation method to gliding motion of bacteria on a layer of power-law nanoslime with heat transfer. J. Comput. Theor. Nanosci. 12(12), 3605–3614 (2015).
Eldabe, N. T., Abou-zeid, M. Y., Mohamed, M. A. & Maged, M. Peristaltic flow of Herschel Bulkley nanofluid through a non-Darcy porous medium with heat transfer under slip condition. Int. J. Appl. Electromagn. Mech. 66, 649–668 (2021).
Eldabe, N. T. & Abou-Zeid, M. Y. Radially varying magnetic field effect on peristaltic motion with heat and mass transfer of a non-Newtonian fluid between two co-axial tubes. Therm. Sci. 22(6A), 2449–2458 (2018).
Eldabe, N. T. M., Abou-zeid, M. Y., Elshabouri, S. M., Salama, T. N. & Ismael, A. M. Ohmic and viscous dissipation effects on micropolar non-Newtonian nanofluid Al2O3 flow through a non-Darcy porous media. Int. J. Appl. Electromagn. 68, 209–221 (2022).
Eldabe, N. T. M., Abou-zeid, M. Y., Ouaf, M. E., Mustafa, D. R. & Mohammed, Y. M. Cattaneo–Christov heat flux effect on MHD peristaltic transport of Bingham nanofluid through a non-Darcy porous medium. Int. J. Appl. Electromagn. Mech. 68, 59–84 (2022).
Mohamed, M. A. & Abou-zeid, M. Y. MHD peristaltic flow of micropolar Casson nanofluid through a porous medium between two co-axial tubes. J. Porous Media 22, 1079–1093 (2019).
Eldabe, N. T. M., Moatimid, G. M., Abou-zeid, M., Elshekhipy, A. A. & Abdallah, N. F. Instantaneous thermal-diffusion and diffusion-thermo effects on Carreau nanofluid flow over a stretching porous sheet. J. Adv. Res. Fluid Mech. Therm. Sci. 72, 142–157 (2020).
Eldabe, N. T. M., Abou-zeid, M. Y., Abosaliem, A., Alana, A. & Hegazy, N. Homotopy perturbation approach for Ohmic dissipation and mixed convection effects on non-Newtonian nanofluid flow between two co-axial tubes with peristalsis. Int. J. Appl. Electromagn. Mech. 67, 153–163 (2021).
Abou-zeid, M. Y. Homotopy perturbation method for couple stresses effect on MHD peristaltic flow of a non-Newtonian nanofluid. Microsyst. Technol. 24, 4839–4846 (2018).
Mansour, H. M. & Abou-zeid, M. Y. Heat and mass transfer effect on non-Newtonian fluid flow in a non-uniform vertical tube with peristalsis. J. Adv. Res. Fluid Mech. Therm. Sci. 61(1), 44–62 (2019).
Eldabe, N. T., Shaaban, A. A., Abou-Zeid, M. Y. & Ali, H. A. Magnetohydrodynamic non-Newtonian nanofluid flow over a stretching sheet through a non-Darcy porous medium with radiation and chemical reaction. J. Comput. Theor. Nanosci. 12(12), 5363–5371 (2015).
El Ouaf, M. & Abou-zeid, M. Electromagnetic and non-Darcian effects on a micropolar non-Newtonian fluid boundary-layer flow with heat and mass transfer. Int. J. Appl. Electromagn. Mech. 66, 693–703 (2021).
Eldabe, N. T., Abou-zeid, M. Y., El-Kalaawy, O. H., Moawad, S. M. & Ahmed, O. S. Electromagnetic steady motion of Casson fluid with heat and mass transfer through porous medium past a shrinking surface. Therm. Sci. 25(1A), 257–265 (2021).
Das, S., Barman, B., Jana, R. N. & Makinde, O. D. Hall and ion slip currents impact on electromagnetic blood flow conveying hybrid nanoparticles through an endoscope with peristaltic waves. BioNanoScience 11, 770–792 (2021).
Vaidya, H. et al. Heat and mass transfer analysis of MHD peristaltic flow through a complaint porous channel with variable thermal conductivity. Phys. Scr. 95, 1–11 (2020).
Vaidya, H. et al. Peristaltic flow of non-Newtonian fluid through an inclined complaint nonlinear tube: Application to chyme transport in the gastrointestinal tract. Eur. Phys. J. Plus 135, 934–948 (2020).
Reddy, K. V., Reddy, M. G. & Makinde, O. D. Thermophoresis and Brownian motion effects on magnetohydrodynamics electro-osmotic Jeffrey nanofluid peristaltic flow in asymmetric rotating microchannel. J. Nanofluids 8(2), 349–358 (2019).
Reddy, M. G. & Makinde, O. D. MHD peristaltic slip flow of Casson fluid and heat transfer in channel filled with a porous medium. Sci. Iran. B 26(4), 2342–2355 (2019).
Eldabe, N. T. M., Moatimid, G. M., Abou-zeid, M., Elshekhipy, A. A. & Abdallah, N. F. Semi-analytical treatment of Hall current effect on peristaltic flow of Jeffery nanofluid. Int. J. Appl. Electromagn. Mech. 7, 47–66 (2021).
Vaidya, H. et al. Peristaltic motion of non-Newtonian fluid with variable liquid properties in a convectively heated non-uniform tube: Rabinowitsch fluid model. J. Enhanc. Heat Transf. 26(3), 277–294 (2019).
Ibrahim, M. G. Concentration-dependent electrical and thermal conductivity effects on magnetoHydrodynamic Prandtl nanofluid in a divergent–convergent channel: Drug system applications. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. https://doi.org/10.1177/09544089221110749 (2022).
Ishtiaq, F., Ellahi, R., Bhatti, M. M. & Alamri, S. Z. Insight in thermally radiative cilia-driven flow of electrically conducting non-Newtonian Jeffrey fluid under the influence of induced magnetic field. Mathematics 10(12), 2007–2018 (2022).
Bhatti, M. M. & Abdelsalam, S. I. Bio-inspired peristaltic propulsion of hybrid nanofluid flow with Tantalum (Ta) and Gold (Au) nanoparticles under magnetic effects. Waves Random Complex Media https://doi.org/10.1080/17455030.2021.1998728 (2021).
Ibrahim, M. G. Adaptive computations to pressure profile for creeping flow of a non-Newtonian fluid with fluid nonconstant density effects. J. Heat Transf. 144(10), 103601 (2022).
Abou-zeid, M. Y., Shaaban, A. A. & Alnour, M. Y. Numerical treatment and global error estimation of natural convective effects on gliding motion of bacteria on a power-law nanoslime through a non-Darcy porous medium. J. Porous Media 18, 1091–1106 (2015).
Abou-zeid, M. Y. & Mohamed, M. A. A. Homotopy perturbation method for creeping flow of non-Newtonian power-law nanofluid in a nonuniform inclined channel with peristalsis. Z. Naturforsch. A. 72, 899–907 (2017).
Eldabe, N. T. M., Abou-zeid, M. Y., Abosaliem, A., Alana, A. & Hegazy, N. Thermal diffusion and diffusion thermo effects on magnetohydrodynamics transport of non-Newtonian nanofluid through a porous media between two wavy co-axial tubes. IEEE Trans. Plasma Sci. 50, 1282–1290 (2021).
Abou-zeid, M. Effects of thermal-diffusion and viscous dissipation on peristaltic flow of micropolar non-Newtonian nanofluid: Application of homotopy perturbation method. Results Phys. 6, 481–495 (2016).
Salahuddin, T., Bashir, A. M., Khan, M. & Elmasry, Y. Activation energy study for peristaltically driven divergent flow with radiation effect. Case Stud. Therm. Eng. 27, 101172 (2021).
Shafique, Z., Mustafa, M. & Mushtaq, A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Results Phys. 6, 627–633 (2016).
Gowda, R. J. P., Kumar, R. N., Jyothi, A. M., Kumara, B. C. & Sarris, L. E. Impact of binary chemical reaction and activation energy on heat and mass transfer of Marangoni driven boundary layer flow of a non-Newtonian nanofluid. Processes 9, 702 (2021).
Ibrahim, M. G. & Fawzy, N. A. Arrhenius energy effect on the rotating flow of Casson nanofluid with convective conditions and velocity slip effects: Semi-numerical calculations. Heat Transf. https://doi.org/10.1002/htj.22712 (2022).
Reddy, K. V., Reddy, M. G. & Makinde, O. D. Heat and mass transfer of a peristaltic electro-osmotic flow of a couple stress fluid through an inclined asymmetric channel with effects of thermal radiation and chemical reaction. Period. Polytech. Mech. Eng. 65(2), 151–162 (2021).
Ibrahim, M. G. Numerical simulation to the activation energy study on blood flow of seminal nanofluid with mixed convection effects. Comput. Methods Biomech. Biomed. Eng. https://doi.org/10.1080/10255842.2022.2063018 (2022).
Ouaf, M. E., Abou-Zeid, M. Y. & Younis, Y. M. Entropy generation and chemical reaction effects on MHD non-Newtonian nanofluid flow in a sinusoidal channel. Int. J. Appl. Electromagn. Mech. 69, 45–65 (2022).
Ismael, A., Eldabe, N., Abouzeid, M. & Elshabouri, S. Activation energy and chemical reaction effects on MHD Bingham nanofluid flow through a non-Darcy porous media. Egypt. J. Chem. 65, 715–722 (2022).
Ibrahim, M., Abdallah, N. & Abouzeid, M. Activation energy and chemical reaction effects on MHD Bingham nanofluid flow through a non-Darcy porous media. Egypt. J. Chem. https://doi.org/10.21608/EJCHEM.2022.117814.5310 (2022).
Liang, Y. Y., Weihs, G. A. F. & Fletcher, D. F. CFD study of the effect of unsteady slip velocity waveform on shear stress in membrane systems. Chem. Eng. Sci. 192, 16–24 (2018).
Nisar, Z., Hayat, T., Alsaedi, A. & Ahmad, B. Significance of activation energy in radiative peristaltic transport of Eyring Powell nanofluid. Int. Commun. Heat Mass Transf. 116, 104655 (2020).
Akbar, N. S. & Nadeem, S. Thermal and velocity slip effects on the peristaltic flow of a six constant Jeffrey’s fluid model. Int. J. Heat Mass Transf. 55, 3964–3970 (2012).
Odibat, Z. M., Bertelle, C., Aziz Alaoui, M. A. & Duchamp, G. H. E. A multistep differential transform method and application to non-chaotic or chaotic systems. Comput. Math. Appl. 59, 1462–1472 (2010).
Hatami, M. & Ganji, D. D. Motion of a spherical particle on a rotating parabola using Lagrangian and high accuracy multistep differential transformation method. Powder Technol. 258, 94–98 (2014).
Ibrahim, M. G. Concentration-dependent viscosity effect on magnetonano peristaltic flow of Powell-Eyring fluid in a divergent-convergent channel. Int. Commun. Heat Mass Transf. 134, 105987 (2022).
Ibrahim, M. G. & Asfour, H. A. The effect of computational processing of temperature- and concentration-dependent parameters on non-Newtonian fluid MHD: Applications of numerical methods. Heat Transf. 55, 1–18 (2022).
Acknowledgements
The authors would like to express their sincere gratitude to the Anonymous Referees for her useful comments.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB).
Author information
Authors and Affiliations
Contributions
M.G.I. wrote the main manuscript text and prepared figures M.Y.A. reviewed the manuscript
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ibrahim, M.G., Abou-zeid, M.Y. Influence of variable velocity slip condition and activation energy on MHD peristaltic flow of Prandtl nanofluid through a non-uniform channel. Sci Rep 12, 18747 (2022). https://doi.org/10.1038/s41598-022-23308-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-23308-4
- Springer Nature Limited
This article is cited by
-
Chemically reacted blood Cu O nanofluid flow through a non-Darcy porous media with radially varying viscosity
Scientific Reports (2024)
-
Empirical modeling and sensitivity analysis of pressure rise per wavelength and frictional forces for the peristaltic flow of Bingham plastic fluids: application of response surface methodology
Journal of Thermal Analysis and Calorimetry (2024)
-
OHAM Analysis on Bio-convective Flow of Partial Differential Equations of Casson Nanofluid Under Thermal Radiation Impact Past over a Stretching Sheet
BioNanoScience (2024)
-
Numerical treatment and global error estimation for thermal electro-osmosis effect on non-Newtonian nanofluid flow with time periodic variations
Scientific Reports (2023)
-
Computational simulation for MHD peristaltic transport of Jeffrey fluid with density-dependent parameters
Scientific Reports (2023)