Abstract
Optimization of thermal conductivity of nanomaterials enables the fabrication of tailor-made nanodevices for thermoelectric applications. Superlattice nanostructures are correspondingly introduced to minimize the thermal conductivity of nanomaterials. Herein we computationally estimate the effect of total length and superlattice period (\(l_{p}\)) on the thermal conductivity of graphene/graphane superlattice nanoribbons using molecular dynamics simulation. The intrinsic thermal conductivity (\(\kappa_{\infty }\)) is demonstrated to be dependent on \(l_{p}\). The \(\kappa_{\infty }\) of the superlattice, nanoribbons decreased by approximately 96% and 88% compared to that of pristine graphene and graphane, respectively. By modifying the overall length of the developed structure, we identified the ballistic-diffusive transition regime at 120 nm. Further study of the superlattice periods yielded a minimal thermal conductivity value of 144 W m−1 k−1 at \(l_{p}\) = 3.4 nm. This superlattice characteristic is connected to the phonon coherent length, specifically, the length of the turning point at which the wave-like behavior of phonons starts to dominate the particle-like behavior. Our results highlight a roadmap for thermal conductivity value control via appropriate adjustments of the superlattice period.
Similar content being viewed by others
Introduction
From the first exfoliation of graphite to graphene synthesis, two-dimensional (2D) nanomaterials have become worth of profound consideration. Graphene, sp2-hybridized carbon known for its honeycomb crystal lattice, shows an outstanding electrical conductivity1, Young's modulus2, thermal conductivity3,4, adsorption capacity5, and surface area6, which are needed for various biological, environmental, and engineering applications7,8,9,10,11,12. However, the semiconductor and transistor applications of graphene are challenging due to its zero bandgap. Furthermore, thermal performance optimization of graphene, for thermoelectric energy conversion and optoelectronic devices, requires chemically-hybridized graphene with some other 2D nanomaterials, such as boron-carbide13,14, nitrogen-carbide15, graphane16, beryllium-oxide17,18, silicone-germanium19, or boron-nitride20,21,22,23,24,25. The resulting heterostructures are named hybrid superlattice nanosheets26.
Graphane, i.e., fully hydrogenated graphene possessing carbon atoms in the form of sp3 hybridization that create C–H bonds, is a semiconductor and insulator having a bandgap in the range of 3.5–4.4 eV27. Graphane can be found in different conformations; however, the so-called chair conformation, in which hydrogen atoms alternate their connection below and above the graphene sheet28, is known as the most stable one. Graphane structure was first experimentally reported in 2009 by Elia et al., obtained through graphene exposure to cold hydrogen plasma at a pressure of 0.1 mbar29. Then, properties of pristine or hybrid forms of graphane were reported in the pertinent literature. Namely, the heat capacity of graphane was estimated by 29.32 ± 0.23 J mol−1 K-1, as predicted using molecular dynamics (MD) simulation by Neek-Amal30. The 2D Young's modulus of graphane was computed to be 245 N m−1 employing density functional theory (DFT), smaller than the value of Young's modulus reported for 340 ± 50 N m−1 graphene31.
Pei et al.32 reported that complete hydrogenation of graphene reduces the thermal conductivity by about 70–80% due to the softening of G-band phonon modes upon the transition of sp2 sp3 bond. Rajabpour et al.33 found the thermal rectification and interface thermal resistance of hybrid graphene-graphane nanoribbons, demonstrating the potential usage of this hybrid nanoribbon as a promising thermal rectifier. The thermal conductivity of multilayer graphene/graphane/graphene heterostructure nanoribbons was also studied using MD simulation by Kim et al.34. They reported that the chemical integration of graphene with graphane creates heteronanosheets where a decrease in the thermal conductivity of graphene to a desirable level by 96% can be obtained. These cases mentioned above indicate the effort of researchers to manipulate the thermal conductivity of such structures towards the fabrication of nanodevices with controlled thermal conductivity. In this regard, superlattice nanostructures are introduced for minimizing thermal conductivity. Such superlattice structure consists of a repeating unit containing different materials with a specified periodic length (\(l_{p}\), superlattice period). The fabricated superlattice has a lower thermal conductivity value than its constituent components. This minimal thermal conductivity phenomenon stems from the competitive nature of wave-like (coherent) and particle-like (incoherent) modes of phonon thermal transport. Namely, as the value of \(l_{p}\) is larger than the phonon coherence length, the incoherent mode of thermal transport dominates the coherent mode such that the minimal thermal conductivity occurs at the point of coherent-incoherent transition35.
Several theoretical research works have been performed to unravel the thermal transport in the superlattice nanostructures. For example, the dependency of thermal conductivity of graphene-hBN superlattice nanoribbons on the superlattice period as well as the total length, based on MD simulation, were examined35. It was found that the thermal conductivity of a nanoribbon with a superlattice period of 3.43 nm was equal to 89 W m−1 K−1, which is lower than the thermal conductivity of either graphene or hBN nanoribbons. Moreover, the effective phonon mean free path (MFP) was estimated to be minimum (32 nm) for the same superlattice period. It was found that the suppression of coherent phonon thermal transport is achieved by increasing the number of interfaces per unit cell. Correspondingly, the Fibonacci expression is enlarged due to the growth of the hindering phonon coherence along the superlattice nanoribbon36. Wang et al.37 resulted in infinite thermal conductivities of 16.08, 15.95, 5.60 W m−1 K−1 for silicene, pure germanene, and silicene-germanene superlattice nanoribbon, respectively. The dependencies of thermal conductivity on the total length, temperature, and the temperature difference between hot and cold baths for the C3N/C2N superlattice nanosheets were studied by Razzaghi et al. through the MD simulation37. They obtained the values of 23.2 W m−1 K−1, and 24.7 nm for the minimum thermal conductivity and the phonon mean free path, respectively, at a superlattice period of 5.2 nm. Moreover, they reported that at a total length larger than 80 nm, the scattering of low-wavelength or high-frequency phonons at interfaces occurs. By contrast, at shorter lengths, the wave interference causes a reduction in the amount of thermal conductivity. According to the performed theoretical studies, it can be understood that the minimum infinite thermal conductivity of superlattice nanoribbons is controlled by the superlattice period and the constituent elements of superlattice structures.
In the present work, we evaluate the thermal properties of a series of lateral graphene/graphane superlattice nanoribbons using MD simulations. The study was conducted with various total lengths and superlattice periods, at a mean reference temperature of 300 K and a temperature difference (ΔT) of 40 K between the two sides. Firstly, we verified the effect of the graphene/graphane sample's total length on the thermal conductivity of the superlattice nanoribbon with different superlattice periods (\(l_{p}\)). Subsequently, the effect of superlattice periods on the intrinsic thermal conductivity and the effective phonon MFP of graphene/graphene superlattice nanoribbon were explored.
Simulation method
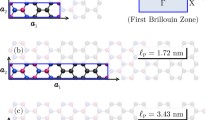
In the current research, MD simulations conducted with the help of the open-source software package LAMMPS (Large-Scale Atomic/Molecular Massively parallel Simulator38) were used to investigate the thermal properties of graphene/graphane superlattice nanoribbons having various superlattice periods (\(l_{p}\) = 1.702, 3.403, and 6.806 nm). The carbon–carbon and carbon–hydrogen bonding interactions were modeled using the adaptive intermolecular reactive empirical bond order (AIREBO) potential39 with a time-step of 0.25 fs. The monolayer superlattice nanoribbons were formed by repeating unit cells of graphene and graphane of the same size, i.e., equal to the superlattice period (\(l_{p}\)), as shown in Fig. 1. The width of all nanoribbons is 8 nm and periodic boundary conditions were considered in X and Y (in-plane) directions.
To correctly estimate the considered superlattice's thermal properties, several MD stages must be performed. The employed procedure within our numerical simulations comprises the following steps:
-
1.
Firstly, energy minimization is performed for repositioning atoms in the constructed nanoribbon.
-
2.
Secondly, an N.P.T. ensemble (constant atom number, pressure, and temperature) with the use of the Nosé-Hoover thermostat and barostat40 is applied to reach zero pressure and a temperature of 300 K in 250 ps.
-
3.
Next, the system was equilibrated via the application of an N.V.T. ensemble (constant atom number, volume, and energy) for 1 ns at 300 K.
-
4.
Finally, the thermal properties of superlattice nanoribbons are computed using the following setup: nanoribbon models are divided into 30 slabs along the X-direction. Atoms present in the left and right edges of superlattice nanoribbon are fixed. The NVE ensemble is applied to the cold and hot boundary slabs region. By applying the N.V.T. ensemble (Nose–Hoover thermostat method), the temperature at the hot and cold slabs is defined as \(T + \Delta T/2\) and \(T - \Delta T/2\), respectively, where T is the mean reference temperature. Finally, the following expression is used for heat flux (\(J_{x}\)) along the X direction41:
$$J_{x} = \frac{{{\raise0.7ex\hbox{${dE}$} \!\mathord{\left/ {\vphantom {{dE} {dt}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${dt}$}}}}{{A_{c} }},$$(1)\(A_{c}\) refers to the cross-sectional area of the nanoribbons (0.34 × 8 nm2), t is the simulation time, and \(E\) corresponds to accumulated energy.
After reaching steady-state conditions, the thermal conductivity for a nanoribbon of length L is calculated from Fourier law as follows:
\(\left\langle . \right\rangle\) refers to time averages and \(\nabla_{x} T\) denotes the temperature gradient in the direction of heat flow.
Results and discussion
The superlattice hybrid nanoribbons inevitably contain the interfaces at which the two alternating media meet each other. The presence of these interfaces and their total number affect heat transfer in these nanoribbons. Firstly, we investigate the effect of an individual interface on heat transfer. Figure 2 depicts the temperature profile of a single unit, graphene/graphane hybrid nanoribbon, with a length of 20.42 nm at room temperature and a temperature difference of 40 K. As we can observe in the same figure, the temperature profile exhibits a discontinuity at X = 11 nm, which coincides with the interface's position. The difference in atomic structures across the interface causes phonon scattering and, consequently, a temperature drop (Tg) of 7.1 K. A similar behavior along the interface of a graphene-boron nitride heterostructure for the steady-state temperature is reported by Li et al.42.
Figure 3 depicts the accumulated energy for the hot and cold slabs in the same graphene/graphane hybrid nanoribbon. Using Fig. 3 we can also compute the heat flux value (\(\left| {\frac{dE}{{dt}}} \right| = 0.512 {\text{keV}}.{\text{ns}}^{ - 1}\)) for the hot and cold slabs. Furthermore, this equality of the absolute amount of energy in the cold and hot baths is expected and aligned with the conservation of energy43.
The interfacial thermal resistance at the grain boundary (Kapitza resistance, \(R_{k}\)) can be calculated as follows44:
\(T_{g}\) denotes the temperature drop at the interface (7.1 K) depicted in Fig. 2 and \(J_{x}\) corresponds to heat flux obtained from Eq. (1). Therefore, the Kapitza resistance at the graphene-graphane interface is equal to 2.59 × 10−11 m2 K W−1.
Thermal conductivity of graphene/graphane superlattice nanoribbon as a function of sample length
The effective thermal conductivity of a nanoribbon having a finite length L, under the simulation above conditions is calculated as follows45:
\(\kappa_{\infty }\) is related to the intrinsic, or length-independent, the thermal conductivity of nanoribbon, and \(\Lambda_{eff}\) corresponds to the effective phonon MFP. The effective phonon MFP corresponds to the length at which thermal conductivity is equal to half the value of the intrinsic thermal conductivity of the sample, i.e., if \(\Lambda_{eff} = L\), then \(\kappa = \frac{{\kappa_{\infty } }}{2}\). Figure 4 depicts thermal conductivity of graphene/graphane superlattice nanoribbons as a function of total length for three superlattice periods (6.806, 5.105, and 2.552 nm) at room temperature and a temperature difference of 40 K. Equation 4 was used to fit the data points and calculate \(\kappa_{\infty }\) and the effective MFP As one may observe in Fig. 4, increasing the total length of the superlattice nanoribbon leads to an increase of thermal conductivity, as it is expected from Eq. (4). This positive correlation can be explained by the vanishing scattering for phonons with long wavelengths. However, after a certain length threshold, thermal conductivity increases slowly and reaches a plateau value which corresponds to \(\kappa_{\infty }\). A similar positive correlation of thermal conductivity with sample's length was observed for BC3/C3N superlattice nanoribbons in the theoretical work performed by Mayelifartash et al.46. A linear behavior (\(\kappa \propto L\)) is exhibited for sample lengths above 50 nm and till approximately 500 nm. Two heat transport regimes (I and II) can be identified: region I, corresponding to the ballistic regime, exhibits phonon MFPs which are larger than the length of nanoribbon and phonons may travel at distances exceeding the coherence length. Region II is the diffusive regime where phonon MFPs are shorter than the total length and thermal conductivity loses gradually its dependence on nanoribbon's length. The gray overlay in Fig. 4, where phonon MFP and total length are of the same magnitude, depicts the ballistic-diffusive transition regime. See47 for more detail about the contribution of ballistic and diffusive components to the total thermal conductivity.
Thermal conductivity and effective phonon MFP as a function of superlattice period
The dependency of the intrinsic thermal conductivity of superlattice nanoribbons on their period can be exploited when designing thermal superlattice nanodevices. Figure 5 demonstrates the dependence of thermal conductivity and effective phonon MFP on superlattice's period. We consider periods ranging from 0.85 to 6.8 nm at room temperature and a temperature difference of 40 K. As indicated in Fig. 5a, the intrinsic thermal conductivity values for all graphene/graphane superlattice periods are less than the thermal conductivity of either graphene or graphane48. Specifically, the thermal conductivity of the superlattice nanoribbon decreases by ≈96.4% and 88% compared to the thermal conductivity of pristine graphene and graphane, respectively. Another interesting observation in the same figure relates to the behavior of \(\kappa_{\infty }\). Initially, the value of \(\kappa_{\infty }\) decreases with increasing superlattice period values till it reaches a minimum value of 144 W m−1 k−1 at \(l_{p}\) = 3.4 nm. Afterwards, a reverse trend is observed. A similar non-monotonic dependency of \(\kappa_{\infty }\) on \(l_{p}\) was also observed for hBN/graphene superlattice nanoribbons in36,49. Furthermore, Farzadian et al.50 reported a similar minimum thermal conductivity value of 155 W m−1 k−1 for graphene/phagraphane superlattice nanoribbons at a superlattice period 12.85 nm.
This minimum thermal conductivity occurs at the transition from coherent to incoherent phonon transport. Before reaching the minimum value of \(\kappa_{\infty }\), the occurrence of Brillouin zone folding and band flattering as a result of phonon wave effect along with the modification of the bulk phonon dispersion relation causes the reduction of phonon group velocities and leads to decreasing thermal conductivity with increasing values of \(l_{p}\)51. After the minimum point, at which particle-like phonons scatter diffusively at the interfaces, increases in \(l_{p}\) facilitate heat transfer, and subsequently thermal conductivity, as thermal resistors (media interfaces) decrease in number. Therefore, the minimum thermal conductivity happens at the length of the wave interference effects and the diffuse interface scattering overlap52.
For further elucidating the dependency trend of thermal conductivity on \(l_{p}\), the concepts of effective phonon MFP (\(\Lambda_{eff}\)) and phonon coherent length are discussed. Effective MFP is defined as the average distance that phonon travels before scattering. Phonon coherent length at which the minimum thermal conductivity occurs corresponds to the length that wave-like behavior of phonons starts to become more significant than particle-like behavior53. As shown in Fig. 5, the phonon coherence length is estimated at 3.4 nm (42 times smaller than the minimum of \(\Lambda_{eff}\) which coincides with the same value of the superlattice period). This means that MFP reaches distances much larger than the coherence length, which is also in agreement with the increasing trend in thermal conductivity depicted in Fig. 4.
The wave-like properties are dominant to the left of the minimum. So, phonons suffer a small influence on the interfaces, and transport is coherent. This explains the reduction of thermal conductivity when increasing \(l_{p}\). To the right of the minimum, particle-like incoherent properties are dominant. Thus easing heat conduction due to the decreasing number of interfaces (thermal resistors) with \(l_{p}\). Indeed, it has been shown that thermal conductivity decreases when the structure periodicity is dominated by wave interference effects and increases when it depends on diffuse interface scattering47,54,55.
As a final stage in this research to achieve a deeper understanding of the interface effect in superlattice nanoribbons, we calculate the phonon density of state (DOS) for two groups of atoms at the left and right sides of the graphene/graphane interface; see Fig. 6. DOS of phonons on each side is obtained by calculating the Fourier transform of the velocity autocorrelation function as shown below:
\(\omega\) is the frequency and \({\text{DOS }}\left( \omega \right)\) denotes the density of states at \(\omega\). Symbols \({\varvec{v}}\left( 0 \right)\) and \({\varvec{v}}\left( t \right)\) correspond to the velocity at time zero and \(t\), respectively. Finally, \(\left\langle . \right\rangle\) represents the average per atom over time.
As can be observed, there is a substantial mismatch between the left and right spectrum. This asymmetry of phonon spectra unravels the interfacial thermal resistance and the asymmetrical phonon scattering at the graphene/graphene interface.
Conclusion
In this study, MD simulations were applied to study the effect of the total length on the thermal conductivity of graphene/graphane superlattice nanoribbons. At the same time, various superlattice periods (\(l_{p}\)) were examined and their effect on the intrinsic thermal conductivity (\(\kappa_{\infty }\)) was established. Furthermore, the behavior pattern for the intrinsic thermal conductivity and the effective phonon MFP of graphene/graphene superlattice nanoribbon with increasing values of the period \((l_{p} )\) was identified and studied.
In terms of the sample's total length effect, it was observed that an increase in total length leads to elevated thermal conductivity values. However, thermal conductivity at considerable lengths becomes independent from the length and reaches a plateau value. Moreover, two regions of heat transport were identified based on the sample's total length. The turning point between these two regions occurs at the neighborhood of 120 nm, which corresponds to the ballistic-diffusive transition regime. With regards to superlattice period variation, a minimum thermal conductivity of 144 W m−1 k−1 is observed at \(l_{p}\) = 3.4 nm. This superlattice period signifies phonon coherent length and corresponds to the length at which wave-like behavior of phonons starts to dominate particle-like behavior. Our results indicate that introducing graphane stripes, at appropriate regular intervals, to a graphene sheet permits the control of the resulting hybrid structure's thermal conductivity. Such manipulation capacity of thermal conductivity values is a promising tool for nanoelectronics.
References
Wu, Z.-S. et al. Synthesis of graphene sheets with high electrical conductivity and good thermal stability by hydrogen arc discharge exfoliation. ACS Nano 3(2), 411–417 (2009).
Young, R. J. et al. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 72(12), 1459–1476 (2012).
Farzadian, O., Spitas, C. & Kostas, K. V. Graphene–carbon nitride interface-geometry effects on thermal rectification: A molecular dynamics simulation. Nanotechnology 32(21), 215403 (2021).
Farzadian, O. et al. Phonon thermal rectification in hybrid graphene-C3N: A molecular dynamics simulation. Nanotechnology 31(48), 485401 (2020).
Srinivas, G. et al. Synthesis of graphene-like nanosheets and their hydrogen adsorption capacity. Carbon 48(3), 630–635 (2010).
Stoller, M. D. et al. Graphene-based ultracapacitors. Nano Lett. 8(10), 3498–3502 (2008).
Revuri, V. & Lee, Y.-k. 2D material-based hybrid nanostructure for diagnosis and therapy. In Biomedical Applications of Graphene and 2D Nanomaterials 143–164 (Elsevier, 2019).
Nalwa, H. S. Handbook of Nanostructured Materials and Nanotechnology, Five-Volume Set (Academic Press, Cambridge, 1999).
Farajpour, A., Ghayesh, M. H. & Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 133, 231–263 (2018).
Zarghami Dehaghani, M. et al. Shape memory thin films of Polyurethane: Does graphene content affect the recovery behavior of Polyurethane nanocomposites?. Polym. Compos. 41(8), 3376–3388 (2020).
Novoselov, K. S. et al. Electric field effect in atomically thin carbon films. Science 306(5696), 666–669 (2004).
Li, X. et al. Graphene in photocatalysis: A review. Small 12(48), 6640–6696 (2016).
Salmankhani, A. et al. A theoretical scenario for the mechanical failure of boron carbide nanotubes. Comput. Mater. Sci. 186, 110022 (2021).
Dadrasi, A. et al. A theoretical insight into the fracture behavior of the edge-cracked polycrystalline BC3 nanosheets. Comput. Mater. Sci. 192, 110345 (2021).
Bagheri, B. et al. Fracture fingerprint of polycrystalline C3N nanosheets: Theoretical basis. J. Mol. Graph. Model. 106, 107899 (2021).
Pumera, M. & Wong, C. H. A. Graphane and hydrogenated graphene. Chem. Soc. Rev. 42(14), 5987–5995 (2013).
Dehaghani, M. Z. et al. Fracture toughness and crack propagation behavior of nanoscale beryllium oxide graphene-like structures: A molecular dynamics simulation analysis. Eng. Fract. Mech. 235, 107194 (2020).
Dehaghani, M. Z. et al. Fracture mechanics of polycrystalline beryllium oxide nanosheets: A theoretical basis. Eng. Fract. Mech. 244, 107552 (2021).
Dehaghani, M. Z., et al. Fracture mechanics of SiGe-nano-sheets using molecular dynamics study: Mechanics of monocrystalline versus polycrystalline structure. Eng. Fract. Mech. 107782 (2021).
Lei, W. et al. Porous boron nitride nanosheets for effective water cleaning. Nat. Commun. 4(1), 1–7 (2013).
Hamed Mashhadzadeh, A., Fereidoon, A. & Ghorbanzadeh Ahangari, M. Atomistic modeling of interfacial interaction between polyvinyl chloride and polypropylene with boron-nitride monolayer sheet: A density functional theory study. Superlattices Microstruct. 111, 23–31 (2017).
Zarghami Dehaghani, M. et al. Insight into the self-insertion of a protein inside the boron nitride nanotube. ACS Omega, 5(49), 32051–32058 (2020).
Bagheri, B. et al. Correlation between surface topological defects and fracture mechanism of γ-graphyne-like boron nitride nanosheets. Comput. Mater. Sci. 188, 110152 (2020).
Dehaghani, M. Z. et al. Boron nitride nanotube as an antimicrobial peptide carrier: A theoretical insight. Int. J. Nanomed. 16, 1837 (2021).
Dehaghani, M. Z. et al. Insight into the self-insertion of a protein inside the boron nitride nanotube. ACS Omega 5(49), 32051 (2020).
Grüneis, A. & Vyalikh, D. V. Tunable hybridization between electronic states of graphene and a metal surface. Phys. Rev. B 77(19), 193401 (2008).
Sahin, H. et al. Graphane. Wiley interdisciplinary reviews. Comput. Mol. Sci. 5(3), 255–272 (2015).
Sofo, J. O., Chaudhari, A. S. & Barber, G. D. Graphane: A two-dimensional hydrocarbon. Phys. Rev. B 75(15), 153401 (2007).
Elias, D. C. et al. Control of graphene’s properties by reversible hydrogenation: Evidence for graphane. Science 323(5914), 610–613 (2009).
Neek-Amal, M. & Peeters, F. Lattice thermal properties of graphane: Thermal contraction, roughness, and heat capacity. Phys. Rev. B 83(23), 235437 (2011).
Topsakal, M., Cahangirov, S. & Ciraci, S. The response of mechanical and electronic properties of graphane to the elastic strain. Appl. Phys. Lett. 96(9), 091912 (2010).
Pei, Q.-X., Sha, Z.-D. & Zhang, Y.-W. A theoretical analysis of the thermal conductivity of hydrogenated graphene. Carbon 49(14), 4752–4759 (2011).
Rajabpour, A., Vaez Allaei, S. & Kowsary, F. Interface thermal resistance and thermal rectification in hybrid graphene-graphane nanoribbons: A nonequilibrium molecular dynamics study. Appl. Phys. Lett. 99(5), 051917 (2011).
Kim, J.-C. et al. Thermal conductivity of graphene/graphane/graphene heterostructure nanoribbons: Non-equilibrium molecular dynamics simulations. Solid State Commun. 328, 114249 (2021).
Luckyanova, M. N. et al. Coherent phonon heat conduction in superlattices. Science 338(6109), 936–939 (2012).
Felix, I. M. & Pereira, L. F. C. Suppression of coherent thermal transport in quasiperiodic graphene-hBN superlattice ribbons. Carbon 160, 335–341 (2020).
Wang, X. et al. Phonon thermal transport in silicone–germanene superlattice: A molecular dynamics study. Nanotechnology 28(25), 255403 (2017).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117(1), 1–19 (1995).
Stuart, S. J., Tutein, A. B. & Harrison, J. A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 112(14), 6472–6486 (2000).
Melchionna, S., Ciccotti, G. & Lee Holian, B. Hoover NPT dynamics for systems varying in shape and size. Mol. Phys. 78(3), 533–544 (1993).
Khadem, M. H. & Wemhoff, A. P. Comparison of Green-Kubo and NEMD heat flux formulations for thermal conductivity prediction using the Tersoff potential. Comput. Mater. Sci. 69, 428–434 (2013).
Li, Y. et al. Mechanical and thermal properties of grain boundary in a planar heterostructure of graphene and hexagonal boron nitride. Nanoscale 10(7), 3497–3508 (2018).
Fooladpanjeh, S. et al. Thermal conductivity of random polycrystalline BC3 nanosheets: A step towards realistic simulation of 2D structures. J. Mol. Graph. Model. 107, 107977 (2021).
Rajabpour, A. & Volz, S. Universal interfacial thermal resistance at high frequencies. Phys. Rev. B 90(19), 195444 (2014).
Schelling, P. K., Phillpot, S. R. & Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 65(14), 144306 (2002).
Mayelifartash, A., Abdol, M. A. & Sadeghzadeh, S. Thermal conductivity and interfacial thermal resistance behavior for the polyaniline (C3N)–boron carbide (BC3) heterostructure. Phys. Chem. Chem. Phys. 23, 13310–13322 (2021).
Li, Z., et al. Size dependence and ballistic limits of thermal transport in anisotropic layered two-dimensional materials. arXiv: Mesoscale and Nanoscale Physics (2017).
Balandin, A. A. et al. Superior thermal conductivity of single-layer graphene. Nano Lett. 8(3), 902–907 (2008).
Felix, I. M. & Pereira, L. F. C. Thermal conductivity of graphene-hBN superlattice ribbons. Sci. Rep. 8(1), 1–10 (2018).
Farzadian, O. et al. Phonon heat transport in two-dimensional phagraphene-graphene superlattice. Int. J. Heat Mass Transf. 182, 121917 (2022).
Chen, X.-K. et al. Phonon wave interference in graphene and boron nitride superlattice. Appl. Phys. Lett. 109(2), 023101 (2016).
Yao, T. Thermal properties of AlAs/GaAs superlattices. Appl. Phys. Lett. 51(22), 1798–1800 (1987).
Zhu, T. & Ertekin, E. Phonon transport on two-dimensional graphene/boron nitride superlattices. Phys. Rev. B 90(19), 195209 (2014).
Karaaslan, Y. Coherent and incoherent phonon thermal transport in group-III nitride monolayer superlattices with Tersoff type interatomic potential. Physica E 140, 115176 (2022).
Mu, X. et al. Coherent and incoherent phonon thermal transport in isotopically modified graphene superlattices. Carbon 83, 208–216 (2015).
Acknowledgements
This work has been funded by the following Nazarbayev University Collaborative Research Projects (C.R.P.s): 1. "Development of smart passive-active multiscale composite structure for earth Remote Sensing Satellites (RSS) of ultrahigh resolution (ULTRASAT)", Grant Award No. 091019CRP2115. 2. "Rapid response fixed astronomical telescope for gamma ray burst observation (RARE)", Grant Award No. 091019CRP2101. The authors are grateful to Dr. Mohammad Reza Saeb for his help in language revision. The authors are grateful to Nazarbayev University Research Computing for providing computational resources for this work.
Author information
Authors and Affiliations
Contributions
M.Z.D. performed the simulation and wrote the first draft. S.H and A.H.M. designed and conceptualized the study. O.F. and K.V.S. developed research methodology and checked chemical interactions/possibility of encapsulation, respectively. A.H.M. developed the theoretical formalism and analyzed the data. C.S and M.R.S. critically revised the manuscript. All authors read, commented on the manuscript, gave the final approval for publication and agreed to be held accountable for the work performed herein.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dehaghani, M.Z., Habibzadeh, S., Farzadian, O. et al. Heat transfer through hydrogenated graphene superlattice nanoribbons: a computational study. Sci Rep 12, 7966 (2022). https://doi.org/10.1038/s41598-022-12168-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-022-12168-7
- Springer Nature Limited