Leaf scale quantification of the effect of photosynthetic gas exchange on Δ₄₇ of CO₂

Abstract

The clumped isotope composition (Δ₄₇, the anomaly of the mass 47 isotopologue relative to the abundance expected from a random isotope distribution) of CO₂ has been suggested as an additional tracer for gross CO₂ fluxes. However, the effect of photosynthetic gas exchange on Δ₄₇ has not been directly determined and two indirect/conceptual studies reported contradicting results. In this study, we quantify the effect of photosynthetic gas exchange on Δ₄₇ of CO₂ using leaf cuvette experiments with one C₄ and two C₃ plants. The experimental results are supported by calculations with a leaf cuvette model. Our results demonstrate the important roles of the Δ₄₇ value of CO₂ entering the leaf, kinetic fractionation as CO₂ diffuses into, and out of the leaf and CO₂–H₂O isotope exchange with leaf water. We experimentally confirm the previously suggested dependence of Δ₄₇ of CO₂ in the air surrounding a leaf on the stomatal conductance and back-diffusion flux. Gas exchange can enrich or deplete the Δ₄₇ of CO₂ depending on the Δ₄₇ of CO₂ entering the leaf and the fraction of CO₂ exchanged with leaf water and diffused back to the atmosphere, but under typical ambient conditions, it will lead to a decrease in Δ₄₇.

Introduction

The carbon dioxide (CO₂) concentration in the atmosphere is controlled by various large exchange fluxes with the bio-, hydro- and geosphere, and by anthropogenic emissions. Important tools for quantifying the different terms of the budget are measurement of the mole fraction and the isotopic composition of CO₂¹. The stable carbon isotope composition allows to distinguish between the CO₂ uptake by the ocean and by plants², and the stable oxygen isotope composition allows to determine the magnitude of the large gross carbon fluxes between the atmosphere and biosphere^3,4,5,6. Recent advancements in precise measurement techniques of ¹⁷O-excess⁷ enable the ¹⁷O-excess, Δ¹⁷O, of tropospheric CO₂ to be used as tracer of terrestrial gross primary production^{8,9,10,11,12,13} or stratospheric influx^14,15,16. In addition, the analysis of radiocarbon has been used to quantify the amount of anthropogenic CO₂ emissions^17,18. Despite these four independent isotopic tracers, the CO₂ budget still remains uncertain. It has been suggested that the abundance of the isotopologue ¹⁸O¹³C¹⁶O in the atmosphere might be a promising new tracer to complement the existing isotope tracers^{19,20,21,22,23}.

The abundance of the double substituted (i.e., contain two rare isotopes) isotopologue ¹³C¹⁸O¹⁶O, compared to its abundance at stochastic isotope distribution for a given bulk composition, is also referred to as the clumped isotopic composition of CO₂ (Δ₄₇, see Sect. “Theory” for definition). One of the main reasons for its applicability as a tracer to constrain CO₂ fluxes is that it is mainly sensitive to the temperature at which the CO₂ is formed or exchanges isotopes with water¹⁹. A disadvantage of using Δ₄₇ is that signals are very small: For typical ambient surface temperatures of 5 to 30 °C, the thermodynamic equilibrium value of Δ₄₇ ranges between 0.90 to 1.04 ‰^19,24,25, so high precision measurements are required. Thermodynamic equilibrium values of Δ₄₇ decrease towards 0 at increasingly higher temperatures, and it is possible to distinguish high temperature (e.g. combustion) from low temperature process (e.g. respiration) using Δ₄₇^19,20,22,26.

It is well established that oxygen isotope exchange between CO₂ and water in the biosphere and hydrosphere is the dominant process controlling the oxygen isotope composition of atmospheric CO₂^27,28. The CO₂–H₂O exchange in soils and leaf water is catalyzed by the enzyme carbonic anhydrase (CA)^27,29,30,31. In the leaf, CO₂–H₂O exchange takes place in the mesophyll, and the mole fraction of the CO₂ at the CO₂–H₂O exchange site is expressed as c_m (see Sects. “CO₂ exchange fluxes during photosynthesis” and “Mesophyll conductance”). Laboratory studies have shown that the rate of exchange between CO₂ and water is the same for δ¹⁸O and Δ₄₇^32,33. This finding suggests that the equilibration between CO₂ and leaf water, soil water or open surface water should affect Δ₄₇ with similar kinetics as δ¹⁸O, but in contrast to δ¹⁸O, Δ₄₇ does not depend on the isotopic composition of the different water pools. The rapid isotope exchange of CO₂ with leaf and surface waters is thought to drive the Δ₄₇ of atmospheric CO₂ towards the thermodynamic equilibrium value^1,19.

Measurements of Δ₄₇ in CO₂ from air samples show that the clumped isotopic composition in the atmosphere is not in thermodynamic equilibrium at the global mean air temperature. For instance, background CO₂ from remote air observatories shows Δ₄₇ values of 0.92 ‰²¹, which is 0.06 ‰ lower than the expected value of 0.98 ‰ for a global mean air temperature of 15°C³⁴. In urban and suburban air, Δ₄₇ values are generally even lower and the variability of the reported Δ₄₇ values was higher, possibly due to input from anthropogenic CO₂ formed in high temperature combustion. In Pasadena, Affek and Eiler²⁰, Affek, et al.²⁶, found Δ₄₇ values between 0.73 and 1.01 ‰, and Eiler and Schauble¹⁹ reported even lower values between 0.62 and 0.93 ‰ from a similar location. Laskar and Liang²² reported Δ₄₇ values between 0.75 and 0.93 ‰ for urban and suburban air in Taiwan.

Eiler and Schauble¹⁹ developed a conceptual model to mathematically describe the effect of air-leaf interaction on the Δ₄₇ signature of atmospheric CO₂. The main assumption is that the carbonic anhydrase catalyzed exchange between CO₂ and H₂O within the mesophyll will imprint a Δ₄₇ value that reflects the effect of leaf temperature on the CO₂ that diffuses back out of the stomata to the atmosphere. In addition, kinetic fractionation during the diffusion into and out of the leaf through the stomata affects Δ₄₇ during photosynthetic gas exchange. Eiler and Schauble¹⁹ proposed that this kinetic isotope fractionation is significant especially for plant species that show a low carbonic anhydrase activity. In this case, the diffusive component during photosynthesis might lead to a depletion in Δ₄₇ of atmospheric CO₂ of about 0.1 ‰ relative to the thermodynamic equilibrium value of CO₂–H₂O exchange alone.

Surprisingly, a recent study, Laskar and Liang²² reported Δ₄₇ measurements of CO₂ sampled in a greenhouse that show enrichment by up to 0.08 ‰ in Δ₄₇ relative to the thermodynamic equilibrium value. The authors attributed this deviation to kinetic effects associated with the photosynthetic exchange, but as described in Eiler and Schauble¹⁹, such a kinetic effect should lead to lower, not higher Δ₄₇ values relative to the thermodynamic equilibrium. Furthermore Laskar and Liang²² concluded that photosynthetic gas exchange would decouple Δ₄₇ and δ¹⁸O in contradiction to the simple CO₂–H₂O exchange model of Eiler and Schauble¹⁹. This discrepancy calls for controlled air-leaf gas exchange experiments to characterize the effect of photosynthesis on Δ₄₇ in detail.

Here, we report results from photosynthetic gas exchange experiments under controlled conditions to quantify the effect of gas exchange on the isotopic composition of CO₂. We investigated the effect on Δ₄₇ of the residual CO₂ (i) for different photosynthetic pathways (C₃ vs. C₄ plants), (ii) for two different values of leaf conductance in C₃ plants, and (iii) for variations in light intensities for one C₃ plant. This choice of plant species and gas exchange conditions enable us to directly test the proposed hypothesis proposed by Eiler and Schauble¹⁹ that CO₂–H₂O exchange and kinetic fractionation with back-diffusion of CO₂ to the atmosphere are the main drivers controlling the Δ₄₇ fractionation effect of photosynthetic gas exchange.

Materials and methods

Theory

Background

Δ₄₇ describes the deviation of the abundance of ¹³C¹⁸O¹⁶O (the dominant isotopologue with nominal mass 47) from the random distribution of all isotopes across all isotopologues in a CO₂ sample with the same bulk isotopic composition²⁴. There are three isotopologues of CO₂ with nominal mass of 47, ¹³C¹⁸O¹⁶O (abundance = 46 × 10^–6), ¹⁷O¹²C¹⁸O (abundance = 1.6 × 10^–6) and ¹⁷O¹³C¹⁷O (abundance = 1.6 × 10^–9)¹⁹. The existing isotope ratio mass spectrometer instruments do not have sufficient mass resolving power to separate these isotopologues. Thus, the measured isotope ratio for nominal mass of 47 is a combination of these three isotopologues. Nevertheless, approximately 97% of the CO₂ with nominal mass 47 is ¹³C¹⁶O¹⁸O and the Δ₄₇ value is mostly referred to as the value of ¹³C¹⁶O¹⁸O isotopologue. Δ₄₇ is calculated as^19,35:

$$\Delta _{{47}} = \frac{{^{{47}} R}}{{^{{47}} R^{*} }} - 1$$

(1)

where R stands for the measured ratio of a rare isotopologue of the indicated mass to the most abundant isotopologue, and R^* is the isotopologue abundance ratio assuming that the heavy isotopes are distributed stochastically over all isotopologues^19,24. In this case, ⁴⁷R^* can be calculated from the isotopologues of mass 44 and 47 as ⁴⁷R* = [47]*/[44]* where [44]* = [¹²C][¹⁶O][¹⁶O] and 47 = 2[¹³C][¹⁶O][¹⁸O] + 2[¹²C][¹⁷O][¹⁸O] + [¹³C][¹⁷O][¹⁷O]. Note that the factor 2 is a symmetry number. This leads to

$${}_{}^{{47}} R^{*} = \frac{{2\left[ {{}_{{\text{}}}^{{13}} {\text{C}}} \right]\left[ {{}_{{\text{}}}^{{16}} {\text{O}}} \right]\left[ {{}_{{\text{}}}^{{18}} {\text{O}}} \right] + \left[ {{}_{{\text{}}}^{{13}} {\text{C}}} \right]\left[ {{}_{{\text{}}}^{{17}} {\text{O}}} \right]\left[ {{}_{{\text{}}}^{{17}} {\text{O}}} \right] + 2\left[ {{}_{{\text{}}}^{{12}} {\text{C}}} \right]\left[ {{}_{{\text{}}}^{{17}} {\text{O}}} \right]\left[ {{}_{{\text{}}}^{{18}} {\text{O}}} \right]}}{{\left[ {{}_{{\text{}}}^{{12}} {\text{C}}} \right]\left[ {{}_{{\text{}}}^{{16}} {\text{O}}} \right]\left[ {{}_{{\text{}}}^{{16}} {\text{O}}} \right]}} = 2{}_{}^{{13}} R{}_{}^{{18}} R + 2{}_{}^{{17}} R{}_{}^{{18}} R + {}_{}^{{13}} R\left( {{}_{}^{{17}} R} \right)^{2}$$

(2)

Measurements of both ¹³R and ¹⁸R (ratios ¹³C/¹²C and ¹⁸O/¹⁶O) require solving Eq. 3.

$$- 3K^{2} \left( {{}_{{\text{}}}^{{18}} R} \right)^{{2\lambda }} + 2K{}_{{\text{}}}^{{45}} R\left( {{}_{{\text{}}}^{{18}} R} \right)^{\lambda } + 2{}_{{\text{}}}^{{18}} R - {}_{{\text{}}}^{{46}} R =0$$

(3)

where K is ¹⁷R_std/(¹⁸R_std) ^λ36 and λ is the three isotope exponent.

¹³R and ¹⁸R can be calculated from the corresponding δ values as ($^{{13}} R = \left( {\delta ^{{13}} {\text{C}}_{{{\text{VPDB}}}} + 1} \right) \times 0.011180$, and $^{{18}} R = \left( {\delta ^{{18}} {\text{O}}_{{{\text{VSMOW}}}} + 1} \right) \times 0.0020052$). It is impossible to measure ¹⁷R of CO₂ directly with traditional gas source isotope ratio mass spectrometry due to the isobaric interference of ¹³C¹⁶O¹⁶O on ¹²C¹⁷O¹⁶O. Variations in the isotope ratios ¹⁸R and ¹⁷R in a sample are closely linked in most common processes via the mass dependent fractionation equation [¹⁸R/¹⁸R_std]^λ = ¹⁷R/¹⁷R_std where std stands for standard³⁶. In this study, a value of 0.528 is used as recommended by^37,38. ¹⁷R was calculated as (${}_{{}}^{{17}} R = \left( {{}_{{\text{~}}}^{{18}} {\text{R}}/0.0020052} \right)^{{0.528}} \times 0.0003799$)^35,37,38. Recently, we have shown that ¹⁷R can be measured independent of ¹³C interference on O fragment ions⁷.

δ¹³C and δ¹⁸O of the sample are calculated from δ⁴⁵ and δ⁴⁶ (i.e. δ¹³C_VPDB ≅ δ⁴⁵_sample + 2 × (¹⁷R/¹³R)_VPDB-CO2 × ( δ⁴⁵_sample − λ × δ⁴⁵_sample) and δ¹⁸O_VPDB-CO2 ≅ [ δ⁴⁶_sample − 0.0021 × δ¹³C_VPDB]/0.99904), where ¹⁷R/¹³R is 0.03516³⁷. The δ value is calculated as follow:

$$\delta ^{{\text{x}}} = \left( {\frac{{^{{\text{x}}} {\text{R}}_{{{\text{sample}}}} }}{{^{{\text{x}}} {\text{R}}_{{{\text{standard}}}} }} - 1} \right)$$

(4)

where x can be 13, 18, 45, 46 and 47 (for ¹³C, ¹⁸O, ¹³C¹⁶O¹⁶O, ¹²C¹⁶O¹⁸O and ¹³C¹⁶O¹⁸O, respectively).

CO₂ exchange fluxes during photosynthesis

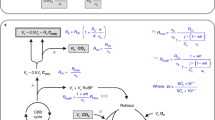
The CO₂ uptake by C₃ plants is schematically illustrated in Fig. 1. Net photosynthetic CO₂ uptake in a leaf generates a concentration gradient from the atmosphere (c_a) to the boundary layer (c_s), intercellular airspace (c_i), the mesophyll cell (c_m) and the chloroplast (c_c), where CO₂ is fixed (in C₃ plants) (see Fig. 1)^39,40,41,42. In the chloroplast, the enzyme RubisCO catalyzes the conversion of carbon dioxide to the three-carbon acid 3-phosphoglyceric acid (3PGA). c_c determines the availability of CO₂ for carboxylation, which is the rate-limiting substrate. The concentration gradient between $c_{{\text{a}}}$ and $c_{\text{c}}$ drives the diffusion of CO₂ into the leaf. The diffusion process can be described mathematically following Fick’s law of diffusion as:

$$A_{{\text{n}}} = g_{{\text{L}}} \left( {c_{{\text{a}}} - c_{{\text{c}}} } \right)$$

(5)

where g_L is the total conductance (inverse of resistance, 1/r_L) of the leaf for CO₂ diffusion. Total g_L is conveniently subdivided into three parts that act in series. The boundary layer conductance (g_b) represents the conductance through a thin layer of near-stagnant air surrounding the leaf; it is a function of air turbulence and leaf area. The stomatal conductance (g_s) varies with the opening and frequency of the stomata. The mesophyll conductance (g_m) quantifies the conductance for transport of CO₂ from the intercellular air space in the leaf to the site of CO₂–H₂O exchange in the mesophyll or the carboxylation in the chloroplast. The latter is expressed as g_m13 and the former is denoted as g_m18, which refers to estimation using δ¹³C and δ¹⁸O respectively (see Sect. “Mesophyll conductance"). A small part of this transport occurs in the gas phase through a residual part of the intercellular air space. The major transport pathway is in the liquid phase, through the wall of the mesophyll cell, the plasmalemma and further into the cell to the site of oxygen exchange between CO₂ and H₂O that is catalyzed by carbonic anhydrase (CA). CO₂ diffuses further through the chloroplast envelope and into the chloroplast where carboxylation occurs^39,40,43.

Figure 1

Schematic illustration of CO₂ exchange fluxes, concentrations and conductivities during photosynthetic gas exchange. Net photosynthetic CO₂ uptake in a leaf generates a concentration gradient over the leaf where c_a is the CO₂ concentration of the air, c_s the CO₂ concentration at the leaf surface, c_i is the CO₂ concentration in the intercellular air space, c_m is the CO₂ concentration in the mesophyll, i.e., the site of CO₂-H₂O exchange and c_c the CO₂ concentration in the chloroplasts, the site of CO₂ uptake. The g_b is the boundary layer conductance of CO₂ from the atmosphere to the leaf surface, the stomatal conductance g_s quantifies the gas exchange through the stomatal opening, g_m13 is the mesophyll conductance to the site of carbon uptake and g_m18 is the mesophyll conductance to the site of CO₂-H₂O exchange.

Mesophyll conductance

For C₃ plants, we used the discrimination against ¹³C (Δ_A¹³C) (Eq. 6) to estimate the mesophyll conductance ($g_{{m13}}$) from the intercellular airspace to the carboxylation site (Eq. 7) as described in⁴⁴. The overall isotope fractionation associated with photosynthetic gas exchange is referred to as discrimination, which quantifies the enrichment or depletion of the isotope composition of CO₂ in the surrounding atmosphere relative to the CO₂ assimilated, see Eq. (6)^42,45,46. Experimentally, the discrimination (Δ_A) is calculated from the isotopic composition and mole fraction of CO₂ entering and leaving the cuvette^47,48,49, as shown in Eq. (6).

$$\Delta _{{\text{Aobs}}}^{{{\text{x}} }} = \frac{{\zeta ~\left( {\delta _{{\text{a}}}^{{\text{x}}} - \delta _{{\text{e}}}^{{\text{x}}} } \right)}}{{1 + \delta _{{\text{a}}}^{{\text{x}}} - \zeta \left( {\delta _{{\text{a}}}^{{\text{x}}} - \delta _{{\text{e}}}^{{\text{x}}} } \right)}}$$

(6)

where x is either 13, 18 or 47 (for ¹³C, ¹⁸O and ¹³C¹⁸O¹⁶O isotope composition, respectively), $\zeta = c_{e} /\left( {c_{e} - c_{a} } \right)$ and c is the mole fraction of the CO₂ entering (index e) and leaving (index a) the cuvette.

$g_{{m13}}$ is calculated from the difference between the observed ¹³C discrimination (Δ_A¹³C_obs) and the discrimination at infinite g_m (c_i = c_c) as:

$${\text{g}}_{{{\text{m}}13}} = \frac{{{\text{A}}_{{\text{n}}} /{\text{P}}}}{{{\text{c}}_{{\text{i}}} - {\text{c}}_{{\text{c}}} }} = \left( {\frac{{1 + {\text{t}}^{{13}} }}{{1 - {\text{t}}^{{13}} }}} \right)\left( {\frac{{{\text{A}}_{{\text{n}}} \left( {{\text{b}} - {\text{a}}_{{\text{m}}} - \frac{{\alpha _{{\text{b}}} }}{{\alpha _{{\text{e}}} \alpha _{{\text{R}}} }}e^{\prime } \frac{{{\text{R}}_{{\text{D}}} }}{{{\text{A}}_{{\text{n}}} }}} \right)}}{{\left( {\Delta _{{\text{A}}}^{{13}} {\text{C}}_{{\text{i}}} - \Delta _{{\text{A}}}^{{13}} {\text{C}}_{{{\text{obs}}}} } \right){\text{Pc}}_{{\text{a}}} }}} \right)$$

(7)

where P is the ambient pressure, t¹³ is a ternary correction factor for ¹³CO₂, b the fractionation due to uptake by Rubisco, and a_m the combination of the fractionations associated with ¹³CO₂ dissolution and diffusion through water, respectively. e’, R_D, $\alpha _{e}$, and $\alpha _{b}$ are the fractionation factor for mitochondrial respiration including the apparent fractionation, the day respiration rate (mitochondrial respiration in the light) the fractionation factor for day respiration with respect to net assimilation and the fractionation factor for C₃ carboxylation, respectively. $\alpha _{R}$ = 1 + (R_D/A_n) × (e’/$\alpha _{e}$). A detailed description of the equations, used parameters and definitions of fractionation factors is provided in Table S1 of the supplementary material.

In C₄ plants, the CO₂ is converted to bicarbonate and fixed to a four-carbon acid catalyzed by phosphoenol pyruvate carboxylase (PEPC) in the mesophyll. Unlike for C₃ plants, it is impossible to estimate mesophyll conductance from Δ_A¹³C for C₄ plants due to the low photosynthetic fractionation^50,51. However, the apparent discrimination against ¹⁸O (Δ_A¹⁸O) can be used to estimate the mesophyll conductance from the intercellular air space to the site of CO₂–H₂O isotope equilibration, $g_{{m18}}$, as described in^{41,47,52,53,54}, for both C₃ and C₄ plants. The analytical expression for estimating $g_{{m18}}$ (Eq. 8) assumes that the degree of equilibration between CO₂ and H₂O is 100%. Some studies have reported that the degree of equilibration can be lower than 100%, especially for C₄ plants, which have a lower CA activity^29,31,47,54. Detailed information is provided in Table S1 of the supplementary material.

$${\text{g}}_{{{\text{m}}18}} = \frac{{{\text{A}}_{{\text{n}}} /{\text{P}}}}{{{\text{c}}_{{\text{i}}} - {\text{c}}_{{\text{m}}} }} = \left( {\frac{{{\text{A}}_{{\text{n}}} /{\text{P}}}}{{{\text{c}}_{{\text{i}}} }}} \right)\frac{{\delta ^{{18}} {\text{O}}_{{\text{A}}} \alpha _{{18{\text{w}}}} + {\text{a}}_{{18{\text{w}}}} - \delta ^{{18}} {\text{O}}_{{\text{m}}} }}{{\delta ^{{18}} {\text{O}}_{\text{i}} - \delta ^{{18}} {\text{O}}_{{\text{m}}} }}$$

(8)

δ¹⁸O_i is δ¹⁸O of CO₂ in the intercellular airspace, $\alpha _{{18w}}$ is the fractionation factor for ¹²C¹⁸O¹⁶O during diffusion and dissolution in water, $a_{{18w}}$ is the discrimination against ¹²C¹⁸O¹⁶O during diffusion and dissolution in water, $a_{{18w}} = \alpha _{{18w}} - 1$, δ¹⁸O_A is δ¹⁸O of the assimilated CO₂ and δ¹⁸O_m is the δ¹⁸O of CO₂ in equilibrium with leaf water at the CO₂–H₂O exchange site. In previous studies, the difference between δ¹⁸O of bulk leaf water and the water at the evaporation site was about 1 to 2 ‰ higher^13,54, but larger differences have also been reported⁵⁵. In this study, we assumed that the δ¹⁸O of leaf water at the CO₂–H₂O exchange site is enriched by 2 ‰ compared to bulk leaf water and the degree of equilibration between CO₂ and leaf water is 100%.

Photosynthetic Δ₄₇ discrimination

The effect of photosynthetic gas exchange on Δ₄₇ depends on the assimilation rate, the various conductances mentioned before and the fraction of CO₂ that diffuses back to the atmosphere after isotope exchange with leaf water. For a laminar boundary layer, diffusion through the boundary layer decreases the Δ₄₇ value of residual CO₂ by an amount equal to the boundary layer diffusive fractionation (+ 0.2 ‰) multiplied by the fraction of CO₂ enters leaves and is fixed (~ 1/3), i.e., 0.07 ‰. In this study, we used a fan (see Sect. “Leaf cuvette set-up”), which creates a turbulent boundary layer with an estimated conductance of 5 mol m⁻² s⁻¹. The boundary layer conductance for the leaf cuvette was determined using wet filter paper from measurements of relative humidity and temperature of air in the cuvette as described in Parkinson ⁵⁶. As a result, the fractionation in Δ₄₇ due to diffusion through the boundary layer is negligible compared to the precision of the measurement (ca. ~ 0.002 ‰). Figure 2 illustrates the effect of photosynthetic gas exchange on Δ₄₇ for two extreme scenarios. The first “uptake dominated” scenario assumes that all the CO₂ entering stomata gets assimilated, leading to c_m/c_a ~ 0 whereas in the second “exchange dominated” scenario all CO₂ diffuses back to the atmosphere after exchange with the leaf water leading to c_m/c_a ~ 1. In the uptake dominated scenario, the resulting Δ₄₇ signal is mainly affected by diffusion, in the exchange dominated scenario the Δ₄₇ signal is dominated by the CO₂–H₂O exchange. A similar scheme for δ¹⁸O is shown in Figure S2 of the supplementary material.

Figure 2

Schematic illustration of the clumped isotope fractionation during air-leaf gas exchange. Δ₄₇ of the CO₂ in the air surrounding the leaf is mainly controlled by CO₂-H₂O exchange and kinetic fractionation during diffusion into and out of the leaf stomata. In the uptake dominated case (c_m/c_a ~ 0), − 0.3 ‰ comes from the fact that diffusion mediated leaf air interaction will reduce the Δ₄₇ value by 0.3 ‰, neglecting other effects. Diffusion only will reduce the Δ₄₇ value by 0.3 ‰ multiplied by the fraction of CO₂ entering the leaf that is assimilated ¹⁹. The boundary layer conductance is large and we have omitted it here.

The fractionation of Δ₄₇ associated with photosynthetic gas exchange (Δ_AΔ_47obs) was calculated in a similar way as $\Delta _{{{\text{Aobs}}}}^{{x}}$ in Eq. (6) from the difference in CO₂ concentration and isotopic composition between the air entering and leaving the leaf cuvette (Eq. 9). For mixing of two different populations of CO₂, Δ₄₇ is not a conserved quantity and the error introduced by adding or subtracting Δ₄₇ values linearly depends on the relative difference in the δ¹⁸O and δ¹³C of the two gases^19,20,57,58. In our study, the maximum difference between the δ¹⁸O and δ¹³C value of the CO₂ entering and leaving the cuvette is 14 ‰ and 4 ‰, respectively. For this rather small range, the error introduced due to linear addition and subtraction of Δ₄₇ values of the CO₂ entering and leaving the cuvette is not significant (< 0.01 ‰).

$$\Delta _{{\text{A}}} \Delta _{{4{\text{7obs}}}} = \frac{{\zeta ~\left( {\Delta _{{47{\text{a}}}} - \Delta _{{47{\text{e}}}} } \right)}}{{1 + \Delta _{{47{\text{a}}}} - \zeta \left( {\Delta _{{47{\text{a}}}} - \Delta _{{47{\text{e}}}} } \right)}}$$

(9)

Leaf cuvette model

To explore the effects of conductance, assimilation rate and back-diffusion of CO₂ to the atmosphere on the Δ₄₇ of ambient CO₂ in detail we used a leaf cuvette model [https://git.wur.nl/leaf-model]⁵⁹ that has been used for the interpretation of Δ¹⁷O measurements in leaf exchange experiments recently¹³. In the model we assumed that CO₂–H₂O exchange in the mesophyll is rapid enough to constantly set Δ₄₇ to thermodynamic equilibrium with the water, i.e., Δ₄₇ = 0.95 ‰ at 20 °C²⁵. Thus, any change in bulk isotopic composition of CO₂ due to assimilation does not affect Δ₄₇¹⁹. Furthermore, CO₂ diffusion into and out of the intercellular air space through the stomata is associated with a fractionation constant of + 0.3 ‰ for Δ₄₇¹⁹ whereas CO₂ diffusion through the boundary layer has a fractionation constant of + 0.2 ‰ for Δ₄₇.

The steady state model considers five compartments: (i) atmosphere (air in the leaf surrounding), (ii) the leaf surface, (iii) the intercellular airspace of the leaf, (iv) the mesophyll cell of the leaf, and (v) the chloroplast (see Fig. 1). The air enters the leaf cuvette at a flow rate F_e and a CO₂ concentration c_e with a well-defined isotopic composition δ_e (where δ can stand for δ¹³C, δ¹⁸O, δ⁴⁷ and Δ₄₇, see Sect. “Background” for definition). The leaf inside the cuvette takes up a portion of the CO₂ and this uptake is associated with an isotope fractionation. The air flowing out of the cuvette has flow rate F_a, CO₂ concentration c_a and isotopic composition δ_a. The photosynthetic uptake in the chloroplasts leads to a concentration gradient between the air surrounding the leaf and the chloroplasts so that there is a net flow of CO₂ from the cuvette into the intercellular airspace, to the mesophyll cell, and finally to the chloroplasts. The corresponding CO₂ concentrations decrease accordingly in the order c_a, c_s, c_i, c_m and c_c. Diffusion, isotopic equilibration with H₂O, CO₂ uptake and mixing between the model reservoirs lead to a change in isotopic composition (δ_a, δ_s, δ_i, δ_m and δ_c). The magnitude of the exchange fluxes between the compartments is defined by the boundary layer conductance g_b, stomatal conductance g_s and the mesophyll conductances g_m18 and g_m13. In the leaf cuvette model, the boundary layer conductance g_b is assumed 5 mol m⁻² s⁻¹, similar to the value determined in the experiment.

Figure 3 shows how the Δ₄₇ value changes between incoming and outgoing CO₂ in the leaf cuvette model for c_m/c_a ratios ranging from 0.3 to 0.9 and Δ₄₇ values of the entering CO₂ between 0.0 ‰ and 1.0 ‰. It is evident that the relative changes are small when Δ₄₇ of the incoming CO₂ is close to the equilibrium value (0.9—1.0 ‰) at ambient temperatures. The changes are much larger if the Δ₄₇ of the incoming CO₂ is close to a random distribution (Δ₄₇ = 0.0 ‰). This motivated us to carry out the gas exchange experiments with isotopically ‘scrambled' (i.e., Δ₄₇ close to zero) CO₂ (see below).

Figure 3

Difference between Δ₄₇ of out- and inflowing CO₂ as function of the fraction of CO₂ diffusing back to the atmosphere (c_m/c_a) calculated with the leaf cuvette model. The black dashed line shows the c_m/c_a ratio where the Δ₄₇ relative difference between the ingoing and outgoing CO₂ becomes zero for the corresponding Δ₄₇ of CO₂ entering the cuvette.

Plant material and growth conditions

Three plant species were used for the experiments, belonging to different functional groups: Sunflower (Helianthus annuus L. cv, Giganteus), Atlantic ivy [Hedera hybernica (Kirchner) Bean (syn. Hedera helix var. hibernica)], and maize (Zea mays L. cv, Torres). The fast-growing annual C₃ species Helianthus is characterized by short-lived leaves with high photosynthetic capacity and conductance for CO₂ diffusion. The other C₃ species, the evergreen Hedera, has long-lived leaves with a lower photosynthetic capacity and conductance. The third species, Zea, has C₄ metabolism, a high photosynthetic capacity and low conductance.

Helianthus and Zea were grown from seed in a growth room at 20 °C, a relative humidity of 70% and a photosynthetic photon flux density (PPFD) of 250 µmol m⁻² s⁻¹ for a day length of 16 h. The first pair of two leaves of Helianthus was used for the experiments when fully grown at three to four weeks after planting. Younger leaves that shaded them were removed. For Zea mays, a section of the fifth or sixth leaf at about two thirds of total leaf length was used at a plant age of around 7 weeks. These leaves were about 5 cm wide, giving a sufficiently large leaf area in the cuvette. Hedera plants were obtained from a grower, pruned to reduce self-shading and further grown in the experimental garden in full daylight. They were used for the experiments in early November 2015 when outside average maximum day temperature during the preceding month was 14 °C. Mature leaves that could be accommodated intact in the cuvette were used for the experiments. For all the experiments, leaves remained attached to the plants during the experiments. Both Helianthus and Zea are watered from tap water whereas Hedera received largely rain water.

Leaf cuvette set-up

The isotopic effect of CO₂ exchange during photosynthesis was investigated with an open gas exchange measurement system similar to the one described by^13,60 (Fig. 4). A controlled flow of air entered and left the leaf cuvette, which had a 7 × 7 cm transparent window on top that limited the maximum width of the leaves that could be accommodated. A fan inside the leaf cuvette increased boundary layer conductance to around 5 mol m⁻² s⁻¹ and mixed the air thoroughly so that the air leaving the cuvette was a representative sample of the air inside. The chamber was illuminated from above by a halogen lamp that allowed control of the PPFD incident on the leaf. Leaf temperature was measured with thermocouples appressed to the abaxial side of the leaf. Water at 20 °C was circulated through the double wall of the cuvette, which stabilized leaf temperature up to 3 °C higher depending on PPFD and transpiration rate (Table 1).

Figure 4

Leaf chamber set-up, modified from Adnew et al. (2020)¹³. A single leaf was placed in the leaf cuvette and the light intensity could be regulated to manipulate the assimilation rate. A gas-mixing unit was used to mix dry synthetic air with scrambled CO₂ with humidified CO₂-free air to obtain an overall CO₂ concentration of the ingoing air of 500 µmol mol⁻¹. The flow rate was adjusted to the photosynthetic activity of the leaf to obtain a CO₂ concentration of about 400 µmol mol⁻¹ at the outlet (0.6 to 1.5 L min⁻¹). CO₂ and H₂O concentrations were monitored with an infrared gas analyzer (IRGA). Once steady state was reached, the outgoing air was sampled in one 2 L and one 1 L glass flasks, in series. The bulk isotope composition (δ¹³C and δ¹⁸O) of the normal CO₂ and scrambled CO₂ are identical.

Table 1 Gas exchange variables and isotopic composition of the bulk leaf water. T_leaf: leaf temperature; c_e: CO₂ concentration of the air entering the leaf cuvette; c_a: CO₂ concentration of the air inside the cuvette and leaving the cuvette; A_n: net assimilation rate; E: transpiration rate; g_s: stomatal conductance for CO₂; c_i: CO₂ concentration in the intercellular airspace; c_c: CO₂ concentration in the chloroplasts (site of CO₂ uptake); c_m: CO₂ concentration in the mesophyll cell; g_m13: mesophyll conductance from the intercellular airspace to the chloroplasts; g_m18 : mesophyll conductance from the intercellular airspace to the CO₂-H₂O exchange site; δ¹⁸O_LW: δ¹⁸O value of the bulk leaf water vs VSMOW (‰). The values in bold are mean and standard deviation for the replicates at different light conditions.

A gas-mixing unit made from ¼ inch stainless-steel tubing was attached to the inlet port of the cuvette. Synthetic dry air with a CO₂ concentration of about 1500 µmol mol⁻¹ was mixed with CO₂-free air of controlled humidity to set the CO₂ concentration of inlet air to 500 µmol mol⁻¹. Air flows were controlled with flow controllers. Two of these mixing units were used, one with untreated CO₂ and the other one with the same CO₂ that was previously isotopically scrambled at 1000 °C (target Δ₄₇ ~ 0.0 ‰, see below for discussion of deviations). The air flow rate was adjusted so that the CO₂ concentration at the outlet (and thus also in the cuvette) was about 400 µmol mol⁻¹. Thus, the decrease in CO₂ concentration in the cuvette as a result of uptake by the leaf was about 100 µmol mol⁻¹. In typical experiments the air flow rate was between 0.6 and 1.5 L min⁻¹ depending on the CO₂ uptake rate of the leaf. It generally took 1 h to reach steady state gas exchange conditions. Gas exchange was measured before and after sampling with an infrared gas analyzer (IRGA) (LI-6262; Li-Cor, Lincoln, NE, USA) operated in the absolute mode. CO₂ and H₂O concentrations of inlet and outlet air were measured subsequently. The IRGA used for CO₂ mole fraction measurements, was calibrated every day with compressed air (dry) which has a known CO₂ mole fraction, and the reference cell was flushed with CO₂-free N₂ gas. For the water mole fraction, the IRGA was calibrated using a dew point mirror, and the reference cell was flushed with CO₂-free N₂ gas. Gas exchange variables were calculated according to von Caemmerer and Farquhar ⁶¹ (see supplementary material Table S1).

The measurements before and after sampling were used to check whether leaves remained sufficiently in steady state over the sampling period, if not, the samples were discarded. The mean value of the two gas exchange measurements (before and after collecting an air sample) were used to calculate the gas exchange parameters. Preparing scrambled CO₂ is labor intensive, as a result we used normal CO₂ during the gas exchange experiment until reaching steady state. After the steady state was reached (i.e. constant CO₂ and H₂O mole fractions) the CO₂ source was switched to the scrambled CO₂ supply (Fig. 4) and we waited 15 min to re-establish steady state conditions. Sampling of air was done by attaching a Mg(ClO₄)₂ dryer (Sigma Aldrich, USA) and 6-L of glass flasks to the outlet of the cuvette. The duration of completely flushing and filling the flasks depended on the flow rate and varied between 20 and 50 min.

We regularly determined the isotopic composition of the entering CO₂ by flushing it through an empty leaf cuvette and sampling the air at the outlet as a blank experiment. We used two different synthetic air cylinders spiked with scrambled CO₂: The first cylinder had a δ¹³C value of − 2.50 ± 0.02 ‰, a δ¹⁸O value of 25.3 ± 0.1 ‰ and a Δ₄₇ value of 0.24 ± 0.02 ‰; the second cylinder had a δ¹³C value of − 2.43 ± 0.03 ‰, a δ¹⁸O value of 25.5 ± 0.2 ‰ and a Δ₄₇ value of 0.07 ± 0.03 ‰ (Table S1, supplementary material). If not indicated differently, these and all further errors reported in this manuscript are 1 σ standard deviation, determined from repeated analysis of samples.

Automated CO₂ extraction from air

We used an automated CO₂ extraction and purification system to prepare the sample CO₂ for ¹³C¹⁸O¹⁶O analysis. The system was mainly manufactured from stainless steel parts and consisted of four main units: (i) an air inlet system, (ii) chemical and cryogenic CO₂ drying units, (iii) a cryogenic CO₂ trap and (iv) a GC column for purification (Fig. 5). The outlet of the extraction line was directly connected to the sample bellows of the mass spectrometer. The design of the air inlet system and the cryogenic water and CO₂ traps were based on an automated CO₂ extraction system dedicated to conventional mass spectrometric isotope analysis of atmospheric CO₂⁶².

Figure 5

Schematic of the automated system for CO₂ extraction from air and purification system. The liquid nitrogen tank is connected to the Dewar using Teflon tube covered with a temperature insulator.

The air inlet system allowed connecting several air samples via an 8-port Valco multiport valve: One position of the multiport valve was capped off and was used as a ‘closed’ position, two positions were generally used for working gas cylinders and the remaining five positions could be used to connect the sample flasks. About 2.5 L of air were required for one analysis. For a few samples we measured duplicates. Prior to an extraction sequence, the analytical system was evacuated up to the flask valves. The outlet of the multiport valve was connected to a mass flow controller (10–100 mL min⁻¹; MKS Instruments) to regulate the gas flow during the extraction system. The flow rate was routinely set to 50 mL min⁻¹ for extracting the CO₂ from air.

In order to minimize exchange with water the gas was thoroughly dried at three different positions in the automated extraction system: (i) before the mass flow controller with a magnesium perchlorate unit, (ii) after the mass flow controller with two cryogenic water traps, and (iii) after the CO₂ trap with a phosphorus pentoxide (P₂O₅) unit. The magnesium perchlorate was filled in a ca. 10 cm long open-end glass tube with 10 mm inner diameter in the central part and ¼” connectors. The drying agent was held in place with glass wool. The cryogenic water traps were made from 25 cm long stainless steel tubes with a diameter of ¼ ” and inner tubes with a diameter of 1/8 ”⁶³. The outer tubes were welded tight at the bottom and electropolished afterwards to reobtain a smooth surface. The inner tubes ended about 0.5 cm above the bottom of the outer tubes to force the air through the entire length of the water trap. To enhance the cold transfer between the outer and inner tube, the inner tubes were slightly bent to touch the outer tubes. The cryogenic water traps were cooled with a mixture of dry ice and ethanol to − 72 °C. The position of the Dewar with the cooling bath was controlled with a hydraulic lift. Due to the relatively large size of the Dewar, the temperature of the cooling bath stayed constant overnight. The (P₂O₅) drying unit consisted of a 10 cm long and 6 mm o.d. wide glass finger containing phosphorous pentoxide (P₂O₅), which was connected via a 1/8″ stainless steel tube to the CO₂ trap. It was immersed in liquid nitrogen using a hydraulic lifter.

The chemical drying units were added to the system at a later stage in an attempt to reduce isotopic re-equilibration during the extraction process (see below). However, also these additional measures did not prevent partial re-equilibration in the extraction line so that we had to correct all Δ₄₇ data for this partial re-equilibration. The size of the corresponding correction was established by frequently analyzing heated and non-heated CO₂ in air standards (see Sect. "Isotopic analysis of CO₂ (δ¹³C, δ¹⁸O and Δ₄₇").

Carbon dioxide (and nitrous oxide) was trapped by immersing the CO₂ trap in liquid nitrogen. The design of the carbon dioxide trap and cooling unit was the same as the cryogenic water trap described above. During extraction, the air was processed through the system with a fore vacuum pump. A mechanical flow restriction (crimped 1/16″ stainless steel tubing) after the CO₂ trap slowed down the flow rate in the CO₂ trap. The crimping was adjusted such that the pressure in the water and CO₂ trap was about 180 mbar at a flow rate of 50 mL min⁻¹.

After trapping the CO₂ in the liquid nitrogen trap, the trap was warmed up to room temperature and the sample CO₂ was frozen to the P₂O₅ trap. Then, the valve on top of the P₂O₅ glass finger was closed and the CO₂ was brought to room temperature for final drying for about 10 min. Afterwards, the CO₂ was transferred to a 1/16″ focusing trap in front of the gas chromatographic column, by immersing this focusing trap in liquid nitrogen. The CO₂ was then released into a helium stream at a flow rate of approx. 25 mL min⁻¹ through the gas chromatographic (GC) column packed with Porapak Q. The GC column was cooled to 20 °C during purification with cold nitrogen gas provided from a liquid nitrogen Dewar, to hold back possible hydrocarbon impurities²⁰ and it was heated up to 250 °C in-between extractions. After passing through the GC column, the CO₂ was trapped in a second 1/16″ trap and the helium was evacuated using the fore and high vacuum pump of the isotope ratio mass spectrometer (IRMS). Finally, the pure CO₂ was warmed to room temperature and injected into the mass spectrometer.

The whole CO₂ extraction line (including the liquid nitrogen cooling) was controlled via LabVIEW (Version 15.0). The LabVIEW software also gave a signal to the IRMS software Isodat (Version 2.0) to start a measurement. Extraction and purification of one sample took about 4.5 h and we generally analyzed two working standards and three samples per day.

Isotopic analysis of CO₂ (δ¹³C, δ¹⁸O and Δ₄₇)

Mass spectrometric analysis of the isotopic composition of the extracted and purified CO₂ was carried out in dual inlet mode on a MAT 253 mass spectrometer (Thermo Fisher Scientific, Germany) with a modified collector unit that allowed simultaneous analysis of the mass-to-charge ratios (m/z) 44, 45, 46, 47, 48 and 49. The overall reproducibility for Δ₄₇ analysis was about 0.04 ‰, determined from replicate measurements of the compressed air cylinder.

The mass spectrometric Δ₄₇ measurements were calibrated relative to CO₂ heated to 1000 °C and CO₂ equilibrated with water at 28°C^25,64. We analyzed heated and water equilibrated CO₂ with a different bulk isotopic composition and determined a slope of 0.0024 for the heated and water-equilibrated gas line (Figure S3, supplementary material). This slope was used to correct for small, negative background effects on m/z 47. The bulk isotopic composition of our in-house reference CO₂ gas was δ¹³C_VPDB = − 2.82 ‰ and δ¹⁸O_VSMOW = − 26.11 ‰ and the maximum δ⁴⁷ difference between the sample and the reference CO₂ was 17 ‰ resulting in a maximum Δ₄₇ bulk isotope composition effect − 0.04 ‰ which is corrected based on heated and equilibration gas slope.

In order to calibrate our δ¹³C, δ¹⁸O and Δ₄₇ measurements of CO₂ in air, we prepared two cylinders of CO₂ in synthetic air as working reference cylinders (Table S2). The first synthetic air cylinder was spiked with CO₂ resulting in a concentration of about 500 µmol mol⁻¹, δ¹³C_VPDB = − 2.76 ‰, δ¹⁸O_VSMOW = 25.65 ‰ and Δ₄₇ =  0.82 ‰. For the second synthetic air cylinder we used scrambled CO₂ with a similar bulk isotopic composition, i.e. δ¹³C_VPDB =  − 2.73 ‰, δ¹⁸O_VSMOW = − 25.83 ‰ but a low clumped isotope signature of Δ₄₇ = 0.11 ‰ and a CO₂ concentration of 400 µmol mol⁻¹.

The clumped isotopic composition of the first air cylinder was determined by analyzing the pure CO₂ directly in the dual inlet system of the IRMS versus the heated and water equilibrated CO₂ samples and versus CO₂ obtained by acid digestion at 70 °C from a set of clumped isotope carbonate standards (ETH1, ETH2, ETH3 and ETH4). Both procedures gave consistent results of Δ₄₇ = 0.82 ± 0.04 ‰. The same CO₂ was then mixed in reference air cylinder 1 with synthetic air. After extracting and purifying the CO₂, we found an average Δ₄₇ value of 0.86 ± 0.04 ‰. The reason for this offset of 0.04 ± 0.04 ‰ might be partial re-equilibration within the extraction line, where full equilibration at room temperature would result in Δ₄₇ = 0.93 ‰.

For preparing the second air cylinder, we heated the pure CO₂ to 1000 °C for more than 2 hours⁶⁴ and then mixed it into synthetic, CO₂-free air. After extracting and purifying the CO₂ from the second cylinder, we determined an average Δ₄₇ value of 0.42 ± 0.04 ‰. The reason for this significant deviation from the expected Δ₄₇ value of 0.03 ‰ is most likely twofold: (i) partial re-equilibration during mixing of scrambled CO₂ with synthetic air, and (ii) partial re-equilibration in the automated CO₂ extraction line. Subsequently, we prepared several other mixtures of heated CO₂ with an expected clumped isotope signature of Δ₄₇ = 0.03 ‰ in synthetic air cylinders. For all cylinders that were prepared this way we found Δ₄₇ values that were at least + 0.26 ‰ enriched in Δ₄₇ relative to the expected value. It is not straightforward to decide whether the clumped signal of a CO₂-in-air standard was altered during the preparation of the air standard or during the CO₂ extraction step. Comparison between the Δ₄₇ of the pure CO₂ and Δ₄₇ value after processing the CO₂-air mixtures through the CO₂ extraction line reveals a Δ₄₇ scale contraction of 24%, i.e. we measure only 76% of the true difference between samples when determining the clumped isotopic composition of CO₂ in air. This apparent scale contraction was highly reproducible over the course of the experiments reported here and we corrected all Δ₄₇ values accordingly. This illustrates that referencing Δ₄₇ measurements for atmospheric CO₂ samples is challenging because there is no Δ₄₇ standard for CO₂-in-air studies available.

The leaf gas exchange samples contained up to about 0.3 µmol mol⁻¹ N₂O. All CO₂ isotope measurements of δ¹³C, δ¹⁸O and Δ₄₇ were corrected for the mass interference from the N₂O isotopologues because N₂O was not separated from CO₂ during the purification step. The amount of N₂O was inferred from the intensity of the N fragment at m/z 14 relative to the intensity of m/z 44²⁰. For typical N₂O mole fractions of 0.3 µmol mol⁻¹, the N₂O correction was approximately + 0.17 ‰ for δ¹³C, + 0.45 ‰ for δ¹⁸O and − 0.13 ‰ for Δ₄₇.

Considering all correction procedures, most notable the 24% Δ₄₇ scale contraction, we obtain an overall reproducibility for repeated extraction of CO₂ from air and subsequent isotopic analysis of 0.08 ‰ for δ¹³C, 0.3 ‰ for δ¹⁸O and 0.045 ‰ for Δ₄₇.

Leaf water extraction and δ¹⁸O analysis

Immediately after sampling of air for Δ₄₇ measurements, the leaf was placed between plastic sheets, its area was measured, and it was enclosed in a vial and frozen. Leaf water was extracted from the leaves by cryogenic vacuum distillation, i.e. the leaf sample was heated in vacuum to 60 °C and the evaporated water was directly frozen in a vial cooled to liquid nitrogen temperature¹³. The distillation process was carried out for at least 4 h to ensure quantitative extraction (West et al., 2006). The δ¹⁸O value of the leaf water was determined by equilibrating CO₂ and water in a GasBench II (Thermo Scientific), and subsequent analysis of the oxygen isotope composition of the equilibrated CO₂ with a Delta V mass spectrometer (Thermo Scientific, Germany). The oxygen isotope composition was calibrated versus VSMOW and SLAP.

Results

Gas exchange data and isotopic composition of leaf water

Gas exchange of Helianthus was characterized by high stomatal conductance relative to the other two species (Table 1). The net assimilation A_n was 12 µmol m⁻² s⁻¹ at a PPFD of 200 µmol m⁻² s⁻¹ and increased to 22 µmol m⁻² s⁻¹ at 700 µmol m⁻² s⁻¹. The net assimilation increased only little further when measured at a PPFD of 1800 µmol m⁻² s⁻¹ (25 µmol m⁻² s⁻¹). c_i/c_a decreased with increasing irradiance, from 0.82 (at PPFD of 200 µmol m⁻² s⁻¹) to 0.75 (at 1800 µmol m⁻² s⁻¹).

Hedera was measured at a PPFD of 700 µmol m⁻² s⁻¹ only where A_n was lower than that of the other two species (15 µmol m⁻² s⁻¹). Compared to Helianthus at the same PPFD, the stomatal conductance g_s was much lower (0.08 mol m⁻² s⁻¹), causing a clearly lower c_i/c_a ratio (0.41) (Table 1). The C₄ species Zea was also measured at 700 µmol m⁻² s⁻¹ only where A_n was the highest of the three (28 µmol m⁻² s⁻¹) but g_s was rather low (0.13 mol m⁻² s⁻¹) causing the lowest c_i/c_a ratio of the three species, (0.32) (Table 1).

For Helianthus, mesophyll conductance calculated using Δ_A¹³C (g_m13) increased with light intensity whereas the mesophyll conductance measured using Δ_A¹⁸O (g_m18) did not show a clear correlation with the light intensity (Table 1 and Figure S2). Our estimates of g_m18 had relatively larger errors compared to g_m13 (Table 1) and the values were larger (Table 1). For Helianthus, the g_m18 estimates were 1.3 to 2.5 times larger and for Hedera 1.5 times.

The δ¹⁸O value of the bulk leaf water of Helianthus varied between 4.3 and 6.9 ‰ with an average value of 6 ± 1 ‰. For Hedera, the bulk leaf water isotopic composition was δ¹⁸O = 3.1 ± 1.6 ‰. The relative difference in the δ¹⁸O value of the bulk leaf water between the Helianthus and Hedera is due to the difference in the δ¹⁸O of source water. For Zea, the bulk leaf water isotopic composition of the leaf part inserted in the cuvette was δ¹⁸O = 20.5 ± 1.3 ‰. We used a section of the Zea leaves at about 1/3 from the tip for gas exchange experiments and such high enrichments in δ¹⁸O of leaf water compared to the source water are typical for sections towards the tip of elongated leaves (see, ⁶⁵) and at higher vapor pressure deficit⁶⁶.

Effect of photosynthetic gas exchange on the isotopic composition of CO₂

For Helianthus Δ₄₇ increased from 0.24 ‰ in the incoming air to 0.50 ‰ to 0.61 ‰ in the outgoing air, at a c_m/c_a ratio of 0.66 to 0.78 (Table 1 and 2). For Hedera, at a c_m/c_a ratio of 0.28, the change in Δ₄₇ between incoming and outgoing air was more variable than for the other species at similar light intensity. The average change of all the experiments under similar conditions is insignificant (from 0.24 ‰ to 0.22 ‰). For Zea, at lower c_m/c_a ratio (0.20), results were more consistent and no statistically significant decrease in Δ₄₇ between incoming and outgoing air was observed (Table 1 and 2).

Table 2 Isotopic composition of the CO₂ entering and leaving the leaf cuvette and the resulting isotopic discrimination against the isotopologues ¹³C¹⁶O¹⁶O, ¹²C¹⁸O¹⁶O and ¹³C¹⁸O¹⁶O given as Δ_A¹³C, Δ_A¹⁸O and Δ_AΔ₄₇. All the isotope and discrimination values are reported in per mill (‰), with respect to VPDB (for δ¹³C) and VSMOW (for δ¹⁸O). The values in bold are mean and standard deviation for the replicates at different light conditions.

When these changes are converted to discrimination (Δ_AΔ₄₇), for Helianthus, we observed an average Δ_AΔ₄₇ of 1.7 ± 0.4 ‰. Slightly negative but non-significant discriminations were observed for Hedera (− 0.07 ± 0.4 ‰), and Zea (− 0.07 ± 0.06 ‰) (Fig. 6a, Table 2). The Δ_AΔ₄₇ correlates strongly with the c_m/c_a ratio, higher Δ_AΔ₄₇ are observed at higher c_m/c_a ratio. The change in Δ₄₇ between CO₂ entering and leaving the cuvette correlates strongly with the change in δ¹⁸O of CO₂ entering and leaving the cuvette, with an R² value of 0.864 (Fig. 6c). The positive correlation between Δ₄₇ and δ¹⁸O of CO₂ indicates that photosynthetic gas exchange affects Δ₄₇ and δ¹⁸O similarly (Fig. 6a).

Figure 6

Effect of photosynthetic gas exchange on Δ₄₇ and δ¹⁸O of CO₂. Δ_AΔ₄₇ (a) and Δ_A¹⁸O (b) during photosynthetic gas exchange experiments as a function of the c_m/c_a ratio. (LL = low light: PPFD = 200 μmol m^− 2 s⁻¹, ML = medium light: PPFD = 700 μmol m⁻² s⁻¹, HL = high light: PPFD = 1800 μmol m⁻² s⁻¹). a) discrimination against ¹³C¹⁸O¹⁶O (Δ_AΔ₄₇). (b) discrimination against ¹²C¹⁸O¹⁶O (Δ_A¹⁸O). (c) Relative difference between Δ₄₇ the CO₂ entering and leaving the cuvette as a function of the difference between δ¹⁸O of CO₂ entering and leaving the cuvette. The solid line is a linear regression fit with a function of (Δ_47a− Δ_47a) = (0.041 ± 0.004) × (δ¹⁸Oa–δ¹⁸Oe)—0.151 ± 0.040. For the leaf cuvette model, we assumed δ¹⁸O = 10 ‰ for the leaf water and a mesophyll conductance of 0.5 mol m⁻² s⁻¹ bar⁻¹.

In addition to the Δ_AΔ₄₇, we also measured Δ_A¹³C and Δ_A¹⁸O (Table 2). The average net carbon isotope discrimination was Δ_A¹³C = 21.6 ± 1.2 ‰ for Helianthus, 10.1 ± 0.7 ‰ for Hedera and 3.6 ± 0.3 ‰ for Zea. The magnitude of Δ_A¹³C also correlates with the c_c/c_a ratio, in agreement with previous studies^13,42,48. As c_c/c_a depends on light intensity, the gas exchange experiments with Helianthus show a slightly higher Δ_A¹³C at low light intensity (22.8 ± 0.6 ‰) compared to mid and high light conditions (21.1 ± 0.9 ‰). The average apparent oxygen isotope discrimination Δ_A¹⁸O was 62 ± 12 ‰ for Helianthus, 18 ± 3 ‰ for Hedera and 21 ± 9 ‰ for Zea. Similar to Δ_A¹³C, Δ_A¹⁸O is higher at low light intensities (78 ± 6 ‰) compared to mid and high light conditions (55 ± 4 ‰) (Table 2, Fig. 6b).

Discussion

The Δ₄₇ value of CO₂ has been suggested as a possible tracer for gross primary production, however two previous studies presented contradicting conclusions on the effect of photosynthesis on the Δ₄₇ value of CO₂ ^19,22. In this study, using a leaf cuvette experiment under controlled conditions (light, CO₂, temperature and humidity) and a leaf cuvette model, we showed that photosynthetic gas exchange can in principle increase or decrease the Δ₄₇ value of CO₂ depending on the Δ₄₇ value of the CO₂ entering the leaf, the CO₂–H₂O exchange temperature and the back-diffusion flux (quantified as c_m/c_a ratio). However, under conditions similar for the current atmosphere, photosynthesis depletes the Δ₄₇ value of atmospheric CO₂.

The photosynthetic effect on Δ₄₇ of the residual CO₂ for the C₃ species Helianthus and Hedera correlated with the CO₂ concentration gradient over the leaf, i.e. c_m/c_a, and the discrimination in Δ₄₇ showed a similar pattern to Δ_A¹⁸O (Fig. 6). The main driver for the discrimination against δ¹⁸O and Δ₄₇ values of CO₂ is isotope exchange with leaf water, and the fractionation associated with the initial fixation by the enzyme RuBisCO (Ribulose-1,5-bisphosphate carboxylase-oxygenase) or PEP (Phosphoenolpyruvate) has no/negligible effect on the δ¹⁸O and Δ₄₇ value of CO₂. Δ₄₇ value is independent of fractionations in the bulk isotope composition (i.e., variations in δ¹⁸O value due to isotope exchange with leaf water and changes in δ¹³C due to metabolic carbon fixation). The lower discrimination in Δ₄₇ by C₄ plant Zea is due to the lower back-diffusion flux (lower conductance and higher assimilation rate) and the fractionation is dominated by diffusion in agreement with the hypothesis of Eiler and Schauble¹⁹. Gas phase diffusion causes a decrease in Δ₄₇ of the residual CO₂¹⁹, see also Fig. 7.

Figure 7

Leaf cuvette model result for Δ₄₇ photosynthetic discrimination. (a) Δ_AΔ₄₇ as a function of c_m/c_a for various value of Δ_47e (see legend). Panel (b) shows the corresponding value for Δ_47a, the black dashed line indicates the Δ₄₇ of CO₂ at the CO₂-H₂O exchange site for the leaf temperature of 20 °C.

For Helianthus, at a c_m/c_a ratio of 0.81, we observed an increase in Δ₄₇ from 0.24 ‰ to 0.68 ‰ (an increase by 0. 44 ‰) for a CO₂ drawdown of 100 µmol mol⁻¹. Eiler and Schauble¹⁹ reported an increase in Δ₄₇ from 0.65 to 0.75 (an increase by 0.1 ‰, i.e. Δ_A Δ₄₇ ~ 0.54 ‰) due to photosynthetic gas exchange for a CO₂ drawdown of 72 µmol mol⁻¹ (from 390 to 318) using Antirrhinum majus with a c_m/c_a ratio of 0.85, which is consistent with our results.

Using the leaf cuvette model, we quantitatively estimated the expected Δ₄₇ discrimination based on the equations discussed in Sect. “Photosynthetic Δ₄₇ discrimination" and the derived concentration gradient between the atmosphere and the site of CO₂–H₂O exchange (c_m/c_a). For the C₃ species, we obtained an excellent agreement between the observed and the predicted change in Δ₄₇, except for one outlier for the experiments with Hedera (Fig. 6 and Figure S5). For Zea, the observed change between outgoing and ingoing CO₂ of − 0.01 ± 0.01 ‰ (the error is standard deviation for the three measurements) was slightly lower than the expected change in Δ₄₇ of about + 0.01 ‰. However, the difference was still of the order of our measurement precession.

The correlation between Δ_AΔ₄₇ and the c_m/c_a ratio and the overall good agreement between observed and predicted Δ_AΔ₄₇ confirm the hypothesis of Eiler and Schauble¹⁹ that CO₂–H₂O exchange and kinetic fractionation control the discrimination. For high CO₂ back-diffusion fluxes, i.e., high c_m/c_a ratios, the magnitude of the in- and outgoing CO₂ flux is almost the same so that the kinetic term due to diffusion cancels out and the Δ₄₇ value of the residual CO₂ is close to the thermodynamic equilibrium value for the respective leaf temperature, i.e. Δ₄₇ = 0.95 ‰ at 20 °C (Fig. 2). At room temperature, the sensitivity of Δ₄₇ to temperature is about 0.005 ‰/°C so that small variations in temperature do not have a large effect. For c_m/c_a ratios close to zero, the back-diffusion flux is small and the kinetic fractionation term due to diffusion into the intercellular airspace induces a negative discrimination in Δ₄₇ of up to − 0.08 ‰ if the ingoing CO₂ has a Δ₄₇ close to 0 ‰.

As mentioned above and illustrated in Fig. 3, we used CO₂ with an artificially diminished Δ₄₇ value in the gas exchange experiments in order to increase the signal, i.e., the Δ₄₇ difference between incoming and outgoing CO₂. After having verified the Eiler and Schauble¹⁹ mechanism, we use our leaf cuvette model to quantify the effect of photosynthesis on Δ_AΔ₄₇ for CO₂ with typical ambient Δ₄₇ values. In ambient air, Δ₄₇ of CO₂ is usually close to or lower than the Δ₄₇ value of CO₂ at the CO₂–H₂O exchange site (Δ₄₇ = 0.95 ‰).

Figure 7 illustrates the calculated dependence of Δ_AΔ_47, as well as Δ_47a on c_m/c_a during gas exchange for Δ_47e values between 0.6 ‰ and 1.1 ‰ to get Δ_47a values between 0.6 ‰ and 1.05 ‰ close to the Δ₄₇ values of atmospheric CO₂ reported in literature^19,20,21,22. A negative Δ_AΔ₄₇ means that $_{{47{\text{a}}}} < _{{47{\text{e}}}}$ (Eq. 9), i.e., photosynthetic gas exchange would decrease ambient Δ₄₇ values, whereas a positive Δ_AΔ₄₇ would increase ambient Δ₄₇ values. Figure 7a shows that Δ_AΔ₄₇ is mostly negative, thus photosynthetic gas exchange generally acts to decrease Δ₄₇ except for situations in which ambient Δ₄₇ is at the low end of reported values and c_m/c_a ratios are very high (indicating very slow assimilation rates).

At very low c_m/c_a ratio, i.e., the diffusion limited case, Δ_AΔ₄₇ is controlled by the diffusional fractionation. Figure 7a shows that Δ_AΔ₄₇ converges to − 0.5 ‰ as c_m/c_a approaches 0, independent of the incoming CO₂. As indicated in Fig. 2, the theoretically calculated Δ₄₇ fractionation associated with diffusion is Δ_47a–Δ_47e = − 0.3 ‰ when all CO₂ that enters the stomata is assimilated. In our leaf cuvette model where we assume a CO₂ drawdown from 500 to 400 ppm (ζ = 500 / (500–400) = 5), this translates to Δ_AΔ₄₇ ≈ ζ × (Δ_47a—Δ_47e) =− 1.5 ‰). The fact that the model assumes that 2/3 of the CO₂ leave the stomata again without exchanging isotopes explains quantitatively why the diffusion limited endmember is ζ × (Δ_47a—Δ_47e)/3 = − 0.5 ‰, independent of the Δ₄₇ of CO₂ entering the cuvette. Figure 7a shows that in this limit the value of Δ_47a depends very strongly on Δ_47e.

For the other extreme scenario c_m/c_a ≈ 1, Δ_47a converges to the Δ₄₇ value of CO₂ at the CO₂–H₂O exchange site (Δ₄₇ = 0.95 ‰), independent of the Δ₄₇ value of incoming CO₂. This reflects the exchange dominated case in Fig. 2. In this case, Δ_AΔ₄₇ strongly depends on Δ_47e value of the CO₂, for instance Δ_AΔ₄₇ will be ≈ 0.00 ‰ and ≈ − 0.75 ‰ for Δ_47e of 0.95 ‰ and 1.1 ‰, respectively. This is similar to what Adnew et al.¹³ showed for the ¹⁷O-excess of CO₂ in gas exchange experiments.

The leaf cuvette model calculations show that in principle photosynthetic gas exchange can deplete or enrich the Δ₄₇ depending on the initial Δ₄₇ value of the CO₂ in the air surrounding the leaf, leaf temperature (via the Δ₄₇ value at the exchange site) and the fraction of CO₂ exchanged and diffused back to the atmosphere. However, photosynthesis will enrich Δ₄₇ only if the Δ₄₇ value of the CO₂ entering the leaf is far lower than the Δ₄₇ value of the CO₂ at the CO₂–H₂O exchange site. In addition, Fig. 7b shows that when $\Delta _{{47{\text{e}}}}$ is lower than the equilibrium value of 0.95 ‰, photosynthetic gas exchange cannot lead to $\Delta _{{47{\text{a}}}}$ values above the equilibrium value. Thus, according to our leaf cuvette model, photosynthesis cannot lead to Δ₄₇ values that are higher than the thermodynamic equilibrium (unless the incoming, i.e. ambient Δ₄₇ values are already higher, in which case they would be reduced). This agrees well with most reported Δ₄₇ values of atmospheric CO₂ which are lower than expected from the CO₂–H₂O equilibrium at the surface temperature^19,20,21.

As a result, an enrichment of up to 0.08 ‰ in Δ₄₇ relative to the thermodynamic equilibrium value reported by Laskar and Liang²² for Δ₄₇ measurements of CO₂ sampled in a greenhouse cannot be explained by photosynthesis based on our leaf cuvette model results, even at the extreme scenario of c_m/c_a ~ 1. In addition, our results show that photosynthetic driven CO₂–H₂O isotope exchange affects Δ₄₇ and δ¹⁸O in a similar way (Fig. 6, Figure S3 and S4) as observed for a simple CO₂–H₂O equilibration experiment^32,33. This does not support the greenhouse experiment results of Laskar and Liang²² where they concluded that photosynthesis decouples δ¹⁸O and Δ₄₇. We suggest that other processes than photosynthetic gas exchange affected the greenhouse gas experiments reported earlier²². Further experiments in similar environments should be carried out to investigate this in more detail.

Our results provide the experimental verification of the isotope exchange model suggested by Eiler and Schauble¹⁹. In particular, we determine how Δ_AΔ₄₇ varies as a function of c_m/c_a. At high c_m/c_a ratio (high back-diffusion flux), the effect of fractionation due to diffusion is negligible and the Δ₄₇ of atmospheric CO₂ will be driven towards the Δ₄₇ of CO₂ at the CO₂–H₂O exchange site. At low c_m/c_a ratio, the diffusion fractionation dominates and photosynthetic gas exchange will generally lower Δ₄₇. For the real atmosphere with Δ₄₇ values slightly lower than the thermodynamic equilibrium set by CO₂–H₂O exchange, photosynthetic gas exchange cannot increase Δ₄₇ above this equilibrium value.

Our results also show that Δ₄₇ and ¹⁸O discrimination are affected in similar ways during photosynthesis, but in contrast to ¹⁸O, the clumped isotope composition is independent of the δ¹⁸O of bulk leaf water. This means that it is not necessary to know the precise isotopic composition of water at the CO₂–H₂O exchange site for calculating Δ_AΔ₄₇. Furthermore, a disequilibrium in Δ₄₇ is often identified more readily than in δ¹⁸O, since Δ₄₇ depends mainly on CO₂–H₂O exchange temperature. As a result, measurements of Δ₄₇ during air-leaf gas exchange experiments may be an alternative method to determine the mesophyll conductance to the site of CO₂–H₂O exchange and/or the degree of equilibration between CO₂–H₂O inside the leaf. The limitation to this approach is that the Δ₄₇ signals are very small and it requires high precision measurements to constrain the relevant parameters significantly under ambient conditions.

For Helianthus, we found g_m13 values of 0.27 ± 0.1 mol m⁻² s⁻¹ bar⁻¹ at a PPFD of 200 μmol m⁻² s⁻¹_, 0.54 ± 0.1 mol m⁻² s⁻¹ bar⁻¹ at a PPFD of 700 μmol m⁻² s⁻¹ and 0.43 ± 0.05 mol m⁻² s⁻¹ bar⁻¹ at a PPFD of 1800 μmol m⁻² s⁻¹, in good agreement with values reported in previous studies^41,43,67,68. These observations confirm earlier findings that the mesophyll conductance is generally lower at low light intensities (Flexas et al., 2007), although we did not observe any significant difference between mid and high light conditions. For Hedera, we found a g_m13 value of 0.20 ± 0.02 mol m⁻² s⁻¹ bar⁻¹ at a PPFD of 700 μmol m⁻² s⁻¹, which is in good agreement with the maximum mesophyll conductance of 0.14 ± 0.01 mol m⁻² s⁻¹ bar⁻¹ for evergreen angiosperms, including observations from the Hedera species^41,43,51,69. The higher mesophyll conductance for Helianthus compared to Hedera might be due to the high mesophyll porosity and thin cell walls of mesophyll cells which facilitate easier movement of CO₂ within intercellular airspaces and across cell walls as reported for evergreen woody plants^70,71.

Mesophyll conductance (g_m18) of Helianthus did not show a clear dependency on PPFD (Table 1 and Figure S2) with on average a value of 0.68 mol m⁻² s⁻¹ bar⁻¹, which is in good agreement with the few values reported in the literature^41,72. For maize, g_m18 = 0.57 mol m⁻² s⁻¹ bar⁻¹, which is within the wide range of 0.169 to 0.9 mol m⁻² s⁻¹ bar⁻¹ reported in literature^41,73,74,75. For Helianthus and Hedera, g_m18 is on average 1.7 times g_m13 confirming that CO₂–H₂O exchange occurs in the mesophyll cell, i.e., before the carboxylation site, in agreement with previous findings^41,47,49,54.