Introduction

Fragile X syndrome (FXS) is the leading monogenic cause of autism and intellectual disabilities, and reflects loss of function mutations in the RNA binding protein, Fragile X Mental Retardation Protein (FMRP)1,2,3,4. Since the generation of the first mouse model of FXS5, a large number of neural phenotypes have been associated with the syndrome including: abnormalities in dendritic spine morphology and stabilization6,7,8,9,10,11,12, altered short- and long-term forms of synaptic plasticity13,14,15,16,17,18,19,20, abnormal axonal development19,21,22, changes in interneuronal connectivity23,24, channelopathies16,25,26,27,28,29,30,31, and imbalanced excitation/inhibition24,32,33,34,35,36,37,38,39,40,41,42,43,44.

The sheer diversity of reported neural phenotypes highlights the challenge in determining which phenotypes are a primary consequence of the absence of FMRP, from those that reflect indirect secondary neural phenotypes. These secondary neural phenotypes could reflect: (1) compensatory and homeostatic mechanisms, i.e., genetic redundancy and homeostatic plasticity engaged to compensate for the primary consequences of the lack of FMRP44,45,46; or (2) normal forms of plasticity shaped by experiential differences, including differences in sensory exploration, social interactions and maternal care. Indeed, it is increasingly recognized that some of the neural phenotypes reported in animal models of FXS and autism spectrum disorder (ASD) may reflect compensatory mechanisms or differential developmental experiences44,45. For example, it is well established that early differences in sensory experience, social interactions and maternal rearing, can alter numerous neural properties throughout life47,48,49,50,51,52,53. As a result of decreased social interactions, young FMRP-deficient animals could in effect inhabit an impoverished sensory environment. Indeed, it is also well established that in mouse models of FXS and ASD, animals experience differences in social interactions, sensory experience, and maternal care54,55,56,57,58,59. Thus, in addition to the possibility that some neural phenotypes may reflect compensatory plasticity, some phenotypes may be a consequence of normal forms of plasticity differentially shaped experiential differences.

One approach towards disentangling neural phenotypes that are a direct consequence of the absence of FMRP and those that reflect experiential differences is to study network activity and plasticity in isolated circuits that develop ex vivo. Cortical organotypic slices are ideally suited towards this goal since they maintain much of the neural circuitry features of in vivo cortical circuits and recapitulate many aspects of in vivo development60,61,62. For example, ex vivo development of organotypic slices recapitulates the transition from early quiescent networks, to networks that exhibit robust spontaneous activity and Up-states63,64. Furthermore, ex vivo cortical circuits have been shown to be capable of performing a number of interesting computations65,66,67,68,69. Thus, ex vivo circuits allow the study of network-level properties while ascertaining that any differential neural phenotypes emerge from within the circuit being studied, and decrease the likelihood that the observed phenotypes are a consequence of altered developmental experiences. Furthermore, compared to acute slices, ex vivo circuits are less susceptible to rearing and social interaction differences.

Among the best studied examples of network-level dynamics within cortical circuits are Up-states70,71,72,73, a term that generally refers to network-wide regimes in which neurons transition between quiescent Down-states and stable depolarized states with moderate firing rates that are actively maintained by recurrently generated positive feedback74,75,76. Up-states require the tuning of many cellular and synaptic properties including the ratios of excitation and inhibition75,77,78,79. Similar to in vivo circuits, Up-states in organotypic slices emerge over the course of ex vivo development63,80,81. Up-states have been proposed to have multiple functional roles, including memory consolidation and synaptic homeostasis82,83,84,85,86. And it has been hypothesized that Up-states correspond to the desynchronized regimes of awake cortex87.

A number of studies have examined Up-states in Fmr1-KO circuits as a means to dissect the network-level abnormalities involved in FXS24,34,80,88,89,90. Here, in order to help minimize experiential and compensatory effects, we examine the development and plasticity of Up-states in Fmr1−/y circuits that developed ex vivo. Our results establish a sequence of developmental delays in Fmr1−/y circuits, and importantly show that even when overall Up-state frequency is equivalent between WT and FX circuits, the spatiotemporal structure of the underlying activity is altered. These results are consistent with the notion that FXS may reflect the inability to properly orchestrate the multiple forms of plasticity required to generate stable and reproducible spatiotemporal patterns of neural activity46. We thus used all-optical technique to study how Fmr1−/y circuits adapt to chronic stimulation meant to emulate sensory experience. We find that while homeostatic plasticity of Up-states is normal, a form of ex vivo experience-dependent plasticity, that emulates learning, is altered in Fmr1-KO circuits.

Results

Fmr1–/y circuits exhibit a developmental delay in the emergence of spontaneous activity

Studies in acute slices and in vivo have reported both cortical hyper- and hypoactivity in Fmr1-KO animals4,24,34,38,89,91,92. We thus first examined the emergence of spontaneous network activity in auditory cortical slices that developed ex vivo. We contrasted Fmr1−/y and Fmr1+/y circuits using two-photon Ca2+-imaging at two ex vivo developmental ages: 11–16 DIV and 25–30 DIV (Figs. 1, 2). As exemplified in Fig. 1A,B, GCaMP6f fluorescence across 119 neurons from a Fmr1+/y circuit revealed spontaneous network-wide events. We refer to these network-wide events as Up-states, and have confirmed with whole-cell electrophysiology that these events reflect discrete shifts from a quiescent state in which membrane voltage is close to resting, to depolarized regimes with low firing rates (e.g., Fig. Supplement 1)64,80. Fmr1−/y circuits at 11–16 DIV exhibited reduced activity (Fig. 1C) and mean ΔF/F (0.04 ± 0.004, n = 10) compared to Fmr1+/y circuits (0.11 ± 0.019, n = 9; Mann–Whitney test, p = 0.001; Fig. 1D). Up-state frequency was also significantly decreased in Fmr1−/y (0.006 ± 0.004 Hz, n = 10) compared to Fmr1+/y circuits (0.034 ± 0.009 Hz, n = 9; Mann–Whitney test, p = 0.004; Fig. 1E). Because Fmr1−/y circuits did not exhibit much activity and because Up-state frequency was very low, the Up-state duration was only calculated for Fmr1+/y circuits (3.25 + 0.58 s, n = 9; data not shown).

Figure 1
figure 1

Fmr1−/y circuits exhibit reduced Up-state frequency at 11–16 DIV. (A) Representative field of view of two-photon Ca2+-imaging experiment in an ex vivo slice of the auditory cortex. Red filled circles represent regions of interest (ROIs) of selected neurons. (B) Top: Sample ΔF/F signals of 119 neurons from a Fmr1+/y slice. Note that spontaneous Up-states appear as bouts of synchronous activity across the network. Bottom: Two example traces of changes in GCaMP6f fluorescence intensity (∆F/F) from the Fmr1+/y slice. (C) Same as in B for two separate Fmr1−/y slices. The activity of the first 15 neurons is shown. (D) Mean ΔF/F was significantly reduced in Fmr1−/y circuits (0.04 ± 0.004, n = 10) compared to Fmr1+/y circuits (0.11 ± 0.019, n = 9; Mann–Whitney test, p = 0.001). (E) Up-state frequency is significantly lower in Fmr1−/y (0.006 ± 0.004 Hz n = 10) compared to Fmr1+/y ex vivo circuits (0.034 ± 0.009 Hz, n = 9; Mann–Whitney test, p = 0.004). Here, and for all subsequent box-and-whisker plots, the box boundaries represent the 25–75% (interquartile) range, whiskers represent the range of the non-outlier data points. Outliers (squares) are those that fall 1.5 times the interquartile range above or below the box edges. Lines within the box represents the median.

Full size image
Figure 2
figure 2

Normal network activity and Up-state frequency in Fmr1−/y circuits at 25–30 DIV. (A) Five-minute heat map of ∆F/F signals from a Fmr1+/y ex vivo circuit (top: n = 90) and from a Fmr1−/y circuit (bottom: n = 50). (B) Example ∆F/F traces for 6 representative neurons at 25–30 DIV. The upper and bottom 3 neurons are from a Fmr1+/y and Fmr1−/y slice, respectively. Bold lines above heat maps in (A) (black for WT and red for KO) correspond to the traces in (B). (C) Mean ΔF/F of Fmr1+/y circuits (0.21 ± 0.03, n = 8) was not different from Fmr1−/y circuits (0.24 ± 0.04, n = 11; t-test, p = 0.52). (D) Frequency of Up-states was not different between Fmr1+/y (0.02 ± 0.004 Hz) and Fmr1−/y ex vivo slices (0.03 ± 0.006 Hz; t-test, p = 0.55). (E) Up-states duration was not different between Fmr1+/y (2.70 ± 0.42 s) and Fmr1−/y ex vivo slices (2.94 ± 0.35 s; Mann–Whitney test, p = 0.54).

Full size image

Similar experiments in older slices, revealed that by 25–30 DIV the deficit in network activity had normalized (Fig. 2A,B). That is, there was no difference in mean ΔF/F between Fmr1+/y (0.21 ± 0.03, n = 8) and Fmr1−/y circuits (0.24 ± 0.04, n = 11; Fig. 2C). Similarly, Up-state frequency and duration were not significantly different between WT (0.02 ± 0.004 Hz, 2.70 ± 0.42 s, n = 8) and Fmr1−/y circuits (0.03 ± 0.006 Hz, 2.94 ± 0.35 s, n = 11; Fig. 2D,E). As evident from the ΔF/F traces (Fig. 2A,B), and as expected during Up-states, Ca2+ signals were tightly correlated, but there was no significant difference in the mean cell pairwise correlations between Fmr1−/y (Fisher-transformed 0.63 ± 0.03, n = 11) and Fmr1+/y circuits at 25–30 DIV (Fisher-transformed 0.70 ± 0.05, n = 8; data not shown).

Spatiotemporal pattern of activity in Fmr1−/y circuits is less reproducible

These results demonstrate that ex vivo circuits exhibited a signature developmental delay of FXS and suggested that by the 4th week of ex vivo development Up-state dynamics were normal. The term Up-states is used to refer to a number of interrelated forms of neural dynamics, and is sometimes interpreted to refer to bi-stable shifts from a quiescent to active state70,93. However, it has been shown that spontaneous and evoked Up-states, in vivo, in vitro, and ex vivo, can exhibit reproducible spatiotemporal structure63,72,73,77,94. To determine if this was the case ex vivo, we first determined whether there were spatiotemporal patterns of activity within Up-states in WT circuits at 25–30 DIV. In other words, are there distinct spatiotemporal patterns of activity embedded within Up-states that are repeatedly replayed across Up-states? Such spatiotemporal structure could take various forms, including that some neurons could consistently tend to fire at the start of an Up-state while others at the end. To determine if there was detectable structure to the Up-states, we extracted each spontaneous Up-state during an experiment (Fig. Supplement 2A), and calculated the mean similarity (Fig. 3, see “Methods”) across all Up-state pairs in an experiment. We also estimated the similarity index expected by chance based on the statistics of the empirically observed Up-states. Towards this end we shuffled cells within the same Up-state (w/Shuffle), as well between Up-states (b/Shuffle) (Fig. 3, see “Methods”). A one-way ANOVA across the unshuffled and two shuffled conditions revealed that in WT slices there was a significant difference in mean similarity (F2,15 = 23.85, p < 10–4), and that the unshuffled mean similarity index (0.83 ± 0.03, n = 6) was significantly higher than in the shuffled controls (w/ Shuffle, 0.41 ± 0.05; t-tests on Fisher transformed data, p < 10–4 and b/Shuffle, 0.62 ± 0.03; p = 0.001; Fig. 3B). Visual inspection and clustering further confirms this notion and reveal that Up-states exhibit distinct structure (Fig. Supplement 2B,C). These results establish that Up-states in WT ex vivo circuits at 25–30 DIV exhibit reproducible spatiotemporal structure.

Figure 3
figure 3

Up-states in WT circuits exhibit spatiotemporal structure. (A) Three Up-states from a WT circuit. The ‘Within shuffle’ procedure consists of shuffling cells (marked with white boxes) within each Up-state. The ‘Between shuffle’ procedure consists of shuffling between Up-states while maintaining cell identity. The similarity index is then calculated by determining the mean pairwise correlation between Up-states (see “Methods”). (B) A one-way ANOVA across the mean similarity index of the three groups revealed a significant effect (F2,15 = 23.85, p < 10–4). Group WT mean similarity index of Up-states (0.83 ± 0.03; n = 6, black, most to the left group) is significantly higher than the mean similarity index of within shuffled Up-states (0.41 ± 0.05; t-test, p < 0.0001, red, middle group) and between shuffled Up-states (0.62 ± 0.03; t-test, p = 0.001, blue, most to the right group).

Full size image

Having established the presence of spatiotemporal structure in WT circuits, we next asked whether the structure and reproducibility of Up-states in Fmr1−/y circuits was similar to WT circuits. As above, we calculated the pairwise similarity of all Up-states within each slice (Fig. 4A,B). Group analysis revealed that Fmr1−/y circuits exhibited a significantly reduced mean similarity index (0.68 ± 0.01, n = 7) compared to Fmr1+/y circuits (0.83 ± 0.03, n = 6; Mann–Whitney, p = 0.001; Fig. 4C), indicating that the variability of Up-states in Fmr1−/y ex vivo circuits was higher—in other words, the spatiotemporal patterns of activity in FX KO circuits were less stable and less reproducible. We further confirmed that this finding is robust to parameter assumptions or the ΔF/F measure. For example, similarity indices obtained on the z-score fluorescence also revealed that Up-state reproducibility in WT circuits (0.70 ± 0.02, n = 7) was significantly higher than in Fmr1−/y circuits (0.54 ± 0.03, n = 6; t-test, p = 0.001, data not shown). A question that arises from these results is whether Up-states reproducibility undergoes developmental changes. We thus compared similarity index of Up-states from circuits recorded at 11–16 DIV and 25–30 (this analyses cannot be performed in the Fmr1−/y circuits because of the lack of Up-states at 11–16 DIV). Mean similarity index of young (11–16 DIV) Up-states of WT circuits was not significantly different (0.72 ± 0.11, n = 8) from mean similarity index of Up-states of WT circuits at 25–30 DIV (0.83 ± 0.03, n = 6; t-test, p = 0.4), and thus, the structure present in older slices was also present in the younger circuits. Overall, these findings demonstrate that even though the levels of spontaneous activity normalized by the 4th week of ex vivo development, the stability and reproducibility of spontaneous neural dynamics in FMRP-deficient circuits was compromised. In other words, while average levels of activity have normalized the structure of this activity is different in Fmr1−/y circuits.

Figure 4
figure 4

Spatiotemporal patterns of Up-states of Fmr1−/y circuits are more variable. (A) Heat maps of eight concatenated Up-states from a Fmr1+/y circuit. Triangles below heat maps represent the pairwise similarity index between all Up-states, and the overall mean of similarity indices is in black (0.81). (B) Twelve concatenated Up-states from a Fmr1−/y circuit, and similarity indices (mean of 0.63). (C) Group mean similarity index of Up-states in Fmr1+/y circuits (0.83 ± 0.03; n = 6) was significantly higher than mean similarity index of Up-states in Fmr1−/y circuits (0.68 ± 0.01; n = 7; Mann–Whitney test, p = 0.001).

Full size image

Chronic optical stimulation induces normal homeostatic plasticity of up-states

The fact that Up-states are observed both in vivo, in acute slices, and ex vivo, strongly suggests that they represent a fundamental dynamic regime that cortical microcircuits are ontogenetically programmed to seek out. Consistent with this notion, Up-states are homeostatically regulated64,80,95. Thus the developmental delay and decreased reproducibility of Up-states observed in Fmr1−/y circuits could reflect abnormal forms of homeostatic plasticity—or more generally deficits in the ability of cortical microcircuits to adapt in a flexible manner to natural fluctuations and external input. To address this issue we used an all-optical method to chronically stimulate and interrogate cortical circuits to study homeostatic regulation of network dynamics. Slices co-expressing the red-shifted opsin, ChrimsonR, and GCaMP6f. were optically stimulated for 3–4 days at 21–25 DIV (Fig. 5A,B). A concern, however, with this all-optical method is the potential interaction between GCaMP6f and ChrimsonR activation—particularly whether ChrimsonR-positive cells are activated during two-photon scanning. To directly examine this issue, we performed simultaneous whole-cell recording and two-photon Ca2+-imaging of cells co-expressing GCaMP6f and ChrimsonR (Fig. Supplement 3). In 4/4 independent experiments, onset of two-photon scanning (920 nm) did not activate ChrimsonR-positive cells as can be seen by the absence of a voltage deflection of the membrane potential at laser onset (Bottom black trace; Fig. Supplement 3).

Figure 5
figure 5

Normal homeostatic plasticity of spontaneous activity in Fmr1−/y circuits. (A) Schematic of the all-optical chronic stimulation paradigm used for the induction of homeostatic plasticity of spontaneous activity. Slices co-expressing GCaMP6f and ChrimsonR were stimulated for 4 days. Left panel shows co-expression of ChrimsonR-tdTom (double lines in red) expression with GCaMP6f (green stripes inside triangles) somatic expression. (B) DAPI stained slice showing ChrimsonR-tdTom (red) expression with GCaMP6f (green) somatic expression. (C) Spontaneous activity was measured from COS (chronic optical stimulation) and control (unstimulated) slices using two-photon Ca2+-imaging. Mean ∆F/F was significantly reduced following COS in both Fmr1+/y and Fmr1−/y circuits (Two-way ANOVA: F1,24 = 33.16, p = 10–6), with no significant interaction between genotype and stimulation. A significant reduction in mean ∆F/F of COS Fmr1+/y circuits (0.04 ± 0.008, n = 7) was found compared to control Fmr1+/y (0.1 ± 0.01, n = 7; t-test, p < 0.001). A similar reduction was also found in the mean ∆F/F of COS Fmr1−/y (0.04 ± 0.006, n = 7) compared to control Fmr1−/y (0.14 ± 0.02, n = 7; t-test, p = 0.001). Black filled boxes (most to the left) are from control Fmr1+/y slices, gray empty boxes (second to the left) are from COS Fmr1+/y, red filled boxes (third to the left) are from control Fmr1−/y and pink empty boxes (most to the right) are from COS Fmr1−/y. (D) Similarly, COS resulted in a significant reduction of Up-state frequency in both genotypes: Up-state frequency of COS Fmr1+/y (0.01 ± 0.01, n = 7) was significantly reduced compared to control Fmr1+/y (0.05 ± 0.01, n = 7; Mann–Whitney, p = 0.01). A similar reduction in Up-state frequency was found in COS Fmr1−/y (0.004 ± 0.002, n = 7) compared to control Fmr1−/y (0.04 ± 0.009, n = 7; Mann–Whitney test , p = 0.004).

Full size image

Chronic optical stimulation (COS) consisting of a single 50 ms pulse of light every 30 s for 3–4 days produced powerful homeostatic plasticity of Up-states in both Fmr1−/y and Fmr1+/y ex vivo circuits at 25–30 DIV. Specifically, comparison of stimulated and unstimulated control circuits revealed a strong decrease in the mean ∆F/F in both genotypes (Fig. 5C). Importantly, COS also resulted in a significant reduction of Up-state frequency in both genotypes (Fig. 5D). Since chronically optically stimulated slices exhibited very few Up-states, event duration was calculated only for the unstimulated control groups and similar to results in Fig. 2E there was no significant difference between Up-state duration of unstimulated control Fmr1+/y circuits (5.41 ± 1.25 s, n = 7) and Fmr1−/y circuits (8.08 ± 2.47 s, n = 7; data not shown). These results demonstrated that: (1) low frequency (0.033 Hz) chronic optical stimulation produced a profound decrease in Up-state frequency, thus confirming that Up-states are powerfully regulated by external activity; and (2) that homeostatic plasticity of overall network level Up-states appears to be normal in Fmr1−/y circuits.

Fmr1−/y circuits exhibit an impaired ability to adapt to the temporal structure of chronically-presented external stimuli

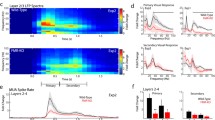
As a learning disability, FXS is defined in part by deficits in the ability to learn38,96, in other words, in the ability of neural circuits to properly adapt in response to the spatiotemporal structure of the patterns they experience. As Fmr1−/y circuits appeared to adapt normally to unstructured external stimulation, we next asked whether Fmr1−/y cortical circuits exhibit deficits in their ability to adapt to structured stimuli. In essence, whether these circuits undergo what can be considered a form of ex vivo learning69. As above we used an all-optical approach to stimulate and interrogate circuits. Ex vivo circuits expressing ChrimsonR and GCaMP6f were trained on an interval paradigm that consisted of two light pulses separated by short or long intervals every 60 s for a duration of 24 h (Fig. 6A). Immediately after training, ten pulses of a single red light were delivered to test evoked network dynamics (Fig. 6B). Fmr1+/y circuits exhibited what can be considered a form of experience-dependent learning: the spatiotemporal structure of the evoked dynamics was dependent on the temporal structure of the experienced stimuli (Fig. 6B–E). Across all WT slices the distribution of evoked Up-states was significantly shorter in the group trained with short intervals compared to the ones trained with long intervals (shifted to the right) (Kolmogorov–Smirnov test, p < 10–6, Fig. 6C). Importantly, group data revealed that in Fmr1+/y circuits the mean Up-states duration were significantly reduced in slices trained with short intervals (0.91 ± 0.05 s, n = 15) compared to slices trained on the long intervals (1.18 ± 0.06 s, n = 19; t-test, p < 0.004; Fig. 6D). Note that while there is an interval specific effect in WT circuits, it is not the case that the duration of the evoked Up-states closely match the trained duration—this is in part expected because of the nonlinear and slow Ca2+ dynamics filters the actual spike patterns and because slices are trained in the incubator in culture media and tested on the rig in ACSF. To further examine the effects of interval training on the spatiotemporal structure of the evoked dynamics, we extracted the peak times (the latencies, see “Methods”) for each cell across all evoked Up-states and contrasted the median peak times in Fmr1+/y slices trained on the short and long intervals. This analysis also revealed a significant interval effect (short: 0.39 ± 0.02 s, n = 15, versus long: 0.49 ± 0.03 s, n = 19; t-test, p = 0.01; Fig. 6E).

Figure 6
figure 6

Interval learning is abnormal in Fmr1−/y circuits. (A) Schematic of the interval learning training and testing paradigm. Slices co-expressing GCaMP6f (green stripes inside triangles) and ChrimsonR (double line in red, surface of triangles) were stimulated with two light pulses separated by short or long interval and then tested using a single pulse. (B) Heat maps of ten concatenated light-evoked responses during testing phase from a Fmr1+/y circuit that was trained with 250 ms interval (short). (C) Cumulative distribution of duration of evoked light responses for Fmr1+/y circuits was significantly different between circuits trained with short compared to long intervals (250: n = 150, 1,000: n = 187, K-S test, p < 10–6). (D) Mean duration of evoked responses of WT circuits trained with short intervals was significantly reduced (0.91 ± 0.05, n = 15) compared to long-trained WT circuits (1.18 ± 0.06, n = 19; t-test, p < 0.004). (E) Average median peak times of WT circuits trained with short intervals was significantly reduced (0.39 ± 0.02, n = 15) compared to circuits trained with long intervals (0.49 ± 0.03, p = 0.01, n = 19; t-test, p = 0.01). (F) Same as C but for Fm1−/y circuits. Distributions were significantly different but did not maintain the expected differential effect between short and long trained at all points (250: n = 166, 1,000: n = 105, K-S test, p = 0.01). (G) Mean duration of evoked responses trained on short intervals (0.97 ± 0.05, n = 17) was not different than long intervals (0.93 ± 0.08, n = 11; t-test, p = 0.62) in Fmr1−/y circuits. (H) Median peak times of Fmr1−/y circuits trained with short intervals was not different (0.41 ± 0.01, n = 17) than the ones trained with long intervals (0.39 ± 0.04, n = 11; t-test, p = 0.61).

Full size image

In contrast to WT circuits that showed differential experience-dependent responses, in the Fmr1−/y circuits there was no significant difference in the mean Up-state duration between the groups trained with short and long intervals (0.97 ± 0.05 s, n = 17 versus 0.93 ± 0.08, n = 11; t-test, p = 0.62; Fig. 6G)—although there was a small difference in the shape of the distribution but as seen in Fig. 6F there was no clear differential effect of the interval training protocol that was used, meaning that the distribution of the long group was not always longer (shifted to the right) (Kolmogorov–Smirnov test, p = 0.01). Additionally, there was no difference in the median peak times between short and long trained groups (0.41 ± 0.01, n = 17 versus 0.39 ± 0.04, n = 11; t-test, p = 0.61; Fig. 6H). We also contrasted these results using a two-way ANOVA, which revealed a significant interaction between the genotype and interval effects for mean Up-state duration and median peak times (F1,58 = 5.94, p = 0.01, F1,58 = 4.32, p < 0.05; respectively) and the absence of main effects. Thus, further confirming that Fmr1−/y circuits did not differentially adapt to the different intervals. Together these results are the first to show that while ex vivo Fmr1−/y circuits exhibit normal ability to homeostatically adapt to changes in external input, they lack the ability to adapt appropriately to the spatiotemporal structure of experienced stimuli—i.e., that FMRP-deficient ex vivo circuits exhibit a deficit in their ability to adapt to experienced stimuli. However, we stress that we cannot explicitly state that the WT circuits are specifically learning the time of the trained intervals, and that Fmr1−/y circuits are not. Rather, we can state that the different training intervals differentially shape the dynamics of WT circuits, and that no such effects were observed in Fmr1−/y circuits.

Discussion

Ultimately the cognitive and behavioral deficits that characterize FXS are expressed at the level of abnormal neural network function and altered patterns of neural activity. While it is known that at the molecular level FXS is caused by the absence of FMRP, to date, the key neurophysiological deficits that ultimately underlie FXS remain unknown4,97. The cause of network-level alterations may eventually be traced to a single synaptic or cellular phenotype, or perhaps more likely, to the interaction between many different neural phenotypes. To date, however, the sheer diversity of neural phenotypes associated with FXS has led to the recognition that some neural phenotypes may reflect indirect experiential or compensatory mechanisms44,45. Here, our focus on plasticity of ex vivo network dynamics offers an approach to study the net effect of many different affected loci on network function. This ex vivo approach offers some novel advantages, such as decreasing the potential influence of some compensatory mechanisms and of potential experiential differences. However, it remains the case that even ex vivo neural phenotypes could arise as a result of secondary compensatory mechanisms engaged in response to the primary consequences of the lack of FMRP. Temporally constrained manipulations using CRISPR or siRNA will offer valuable tools to help further address this possibility in future studies.

Consistent with the neurodevelopmental delays observed in FXS patients and animal models of the disease9,21,32,36,98,99,100,101,102, we observed a delay in the emergence of Up-states in ex vivo Fmr1−/y circuits. The presence of a delay during ex vivo developmental further supports the notion that the lack of FMRP does indeed alter the temporal profile of the ontogenetic program underlying neurodevelopment. However, the delayed development of Up-states that we observed was not a simple developmental delay that eventually completely normalized to match WT dynamics. Even after Up-state frequency and duration normalized, there was increased variability of the spatiotemporal structure of spontaneous network dynamics (Fig. 4). It is difficult to infer the consequences of such increased variability, but this phenotype could be interpreted as impairment in the ability of specific patterns to “consolidate”, and occur as a result of the inability of multiple different forms of plasticity to interact in an orchestrated manner.

As a first step towards testing the hypothesis that specific forms of network-level plasticity may be impaired in Fmr1−/y circuits, we examined the homeostatic regulation of Up-state frequency during late ex vivo development. Chronic optical stimulation over a period of days revealed a robust decrease in spontaneous network dynamics in both WT and Fmr1−/y circuits. These results indicate that mature Fmr1−/y circuits seem to exhibit normal homeostatic plasticity of spontaneous Up-states, suggesting that the mechanisms for normal homeostatic plasticity are functional in the Fmr1-KO ex vivo circuits. It is important to note that unlike homeostatic forms of plasticity such as synaptic scaling, regulation of Up-states likely requires retuning of multiple neural loci including at excitatory and inhibitory synapses78,79,103,104. Thus the presence of normal homeostatic regulation of Up-states suggests that at least some of the learning rules responsible for regulating network dynamics are functional.

A more stringent test of whether the learning rules that govern network dynamics are operational in FMRP-deficient circuits is whether these circuits undergo normal experience-dependent plasticity. That is, if Fmr1−/y cortical circuits are capable of adapting to, and learning, the structure of the stimuli they are exposed to. While it is well established that FXS animals exhibit learning deficits, it is often challenging to directly attribute those deficits to local alterations in cortical circuits. A reduced ex vivo approach provides a mean to study microcircuit-level experience-dependent plasticity, while bypassing potential effects associated with sensory hypersensitivity, neuromodulation, attention, and up/down stream alterations. Thus to emulate an experience-dependent learning protocol we asked if cortical circuits can adapt in an experience-dependent manner to the temporal structure of chronically presented stimuli69.

In WT slices the network dynamics evoked by a single light pulse differed according to the training history of the slice: the duration of evoked dynamics was longer in slices trained with long intervals compared to slices trained with short intervals (Fig. 6). This finding is consistent with previous acute and organotypic slice experiments that have reported in vitro analogs of learning65,66,67,69,105. In contrast to WT circuits however, Fmr1−/y slices did not exhibit differential responses between the slices trained with short and long intervals. These results offer the first suggestion that it may be possible to reproduce experience-dependent deficits that characterize FXS in a reduced ex vivo system.

Future studies will have to determine why Fmr1−/y circuits did not adapt in a stimulus specific manner, and dissect which set of learning rules underlying this deficit. We hypothesize, that this circuit-level experience-dependent deficit may be driven by abnormalities in the ability of multiple learning rules to interact in an orchestrated manner. For example, for computational models of neural networks to converge to stable solutions it is necessary that the multiple learning rules be appropriately tuned in relation to each other. For example in models that contain both homeostatic and associative forms of synaptic plasticity, the learning rates of both learning rules must be appropriately balanced in order to converge to a stable solution106,107,108.

Conclusion

In agreement with previous studies24,34,89,90,92,109, our results further highlight the importance of alterations in local neural dynamics as a major neural phenotype in FXS. A critical issue, however, relates to the underlying cause of the observed changes in neural dynamics. For example, whether the atypical dynamics is the result of “structural” deficits (such as abnormalities in spine number) that persist into adulthood, or rather, of learning rules that govern neuronal properties such as synaptic strength. By studying plasticity of circuit-level dynamics by emulating sensory experience, we established that Fmr1−/y circuits were robustly able to adapt to increased levels of external drive by decreasing spontaneous Up-states. In contrast to WT circuits, however, Fmr1−/y circuits did not adapt in an experience-dependent manner to the chronic presentation of structured external inputs. These results suggest that while homeostatic learning rules governing network activity are normal, there may be deficits in associative learning rules or in the ability of homeostatic and associative learning rules to interact in an orchestrated manner. Finally, the ex vivo experience-dependent learning protocol used here provides a potential reduced system to pinpoint the abnormal learning rules in Fmr1−/y circuits in a targeted manner, while minimizing potential confounds associated with indirect and experiential differences.

Methods

Experimental animals

All experiments were conducted in accordance with the US National Institutes of Health guidelines for animal research, and approved by the Chancellor's Animal Research Committee at the University of California, Los Angeles. Wild-type (WT) male mice (Fmr1+/y, Jackson Labs #004828]) and Fmr1-KO female mice (Fmr1−/−, #004624) on the FVB background (FVB.129P2) were used to establish a colony by breeding heterozygous females (Fmr1−/+) and WT males (Fmr1+/y). Mice were housed in the vivarium under a 12-h light/dark cycle.

Organotypic slice preparation

Organotypic slices were prepared using the interface method110,111 from postnatal day 6–7 Fmr1−/y and Fmr1+/y littermate male mice. Male animals were used because females in these litters were not Fmr1 homozygous. Mice were anesthetized with isoflurane and decapitated. As described previously111, the brain was removed and placed in chilled cutting media. Coronal slices (400 µm thickness) containing mainly primary auditory cortex were cut using a vibratome and placed on Millipore (Billerica, MA) filters (MillicellCM) with 1 ml of culture media. Culture media was changed 1 and 24 h after cutting, and every 2–3 days thereafter. Cutting media consisted of Eagle’s minimum essential medium (EMEM; catalog number 15-010; MediaTech, Herndon, VA) plus (in mM): 3 MgCl2, 10 glucose, 25 HEPES, and 10 Tris base. Culture media consisted of EMEM plus (in mM) 4 glutamine, 0.6 CaCl2, 1.85 MgSO4, 30 glucose, 30 HEPES, 0.5 ascorbic acid, 20% horse serum, 10 U/I penicillin, and 10 µg/l streptomycin. Slices were incubated in 5% CO2 at 35 °C for 7–30 days in vitro (DIV). At the time of brain harvesting a tail sample from each mouse was collected for genotyping (Transnetyx).

Viral transfection

Viral transfection occurred at 1 or 7 DIV. For two-photon Ca2+-imaging, AAV5/9.Syn.GCaMP6f.WPRE.SV40 (UPenn Vector Core, titer: 1013 genomes per ml) was delivered at either 1 DIV for the 11–16 DIV developmental study or at 7 DIV for the 25–30 DIV developmental study. For chronic optical stimulation (COS) experiments both AAV9.Syn.GCaMP6f.WPRE.SV40 (UPenn Vector Core, titer: 1013 genomes per ml) and AAV9.syn.ChrimsonR-tdtomato.WPRE.BGH (UPenn Vector Core, titer: 1013 genomes per ml) were delivered at 7 DIV. Transfection was achieved by gently delivering ~ 1 µl of each viral solution in a glass pipette, with the aid of a manual micromanipulator, to 4–5 different locations in cortical layer (L) II/III. When double transfecting, 1 µl of each virus were mixed and then placed in a single glass pipette for delivery. Experiments were performed two to three weeks after transfection to allow robust viral expression.

Electrophysiology

All experiments (Ca2+-imaging and electrophysiology) were performed at 11–16 or at 25–30 DIV in ACSF composed of (in mM): 125 NaCl, 5.1 KCl, 2.6 MgSO4, 26.1 NaHCO3, 1 NaH2PO4, 25 glucose, and 2.6 CaCl2. This ACSF was formulated to match the standard culture media64. Whole-cell recordings were made from LII/III regular-spiking, supragranular pyramidal neurons using infrared differential interference contrast visualization at 25–30 DIV. The internal solution for whole-cell recordings contained (in mM) 100 K-gluconate, 20 KCl, 4 ATP-Mg, 10 phospho-creatine, 0.03 GTP-Na, and 10 HEPES and was adjusted to pH 7.3 and 300 mOsm. Temperature was maintained at 32–33 °C, and the ACSF perfusion rate was set to 5–6 ml/min. Only cells that satisfied the following criteria were accepted for analysis: resting membrane potential less than − 60 mV, input resistance between 100 and 300 MΩ, and series resistance of less than 25 MΩ. Cells were discarded if resting membrane potential changed by more than 10 mV during the course of recording.

Two-photon calcium imaging

Ca2+-imaging was performed with a galvo-resonant-scanning two-photon microscope (Neurolabware) controlled by Scanbox acquisition software (https://scanbox.org). A Coherent Chameleon Ultra II Ti:sapphire laser (Cambridge Technologies) was used for GCaMP6f excitation (920 nm). We used a 16 × water-immersion lens (Nikon, 0.8 NA, 3 mm working distance). Image sequences were captured using unidirectional scanning at a frame rate of ~ 15–30 Hz. The size of the recorded imaging field was ~ 520 × 800 µm (512 × 796 pixels). GCaMP6f was used because of its relatively fast kinetics, and the relative changes in somatic fluorescence of GCaMP6f were used as a non-linear readout of the neuronal spiking activity112. Regions of interests (ROI) were established in a semi-automated manner, based on manual thresholding of the pairwise pixel correlation (Scanbox). ∆F/F was calculated as (F(t) − F0))/F0, where F(t) was the raw fluorescence filtered with a median filter with a window of 1 s. F0 was the running median F(t) over the previous 10 s window.

Up-state identification and analysis of spatiotemporal structure of neural dynamics from Ca2+ imaging data

For each recorded slice, potential Up-states were identified based on a threshold set at 1.5 above the mean z-scored ΔF/F trace of all neurons. If these events remained above threshold for at least one second, they were classified as Up-states. Onsets and offsets of the population based Up-states were marked, and the ΔF/F profiles of each neuron between one second before Up-state onset and one second after Up-state offset were extracted (Fig. Supplement 2A). The 1 s baseline window is necessary in order for the correlation to pick up deviations from rest. A single Up-state was represented in an NxT matrix, where N corresponds to the number of cells and T as the number of frames. To quantify the overall similarity of these trajectories, we calculated the mean of the pairwise 2D correlation between all Up-states within a slice. We excluded experiments that had less than four Up-states (mean 9 ± 0.97) within the 5-min window of Ca2+ imaging. Importantly, and because the T values of the NxT matrices can be different (differences in Up-state duration), we used the window corresponding to the duration of the longest Up-state in a given pair—in other words the overall duration of Up-states contributed to the measure of Up-state similarity. In order to do so, the shorter Up-state was padded with zeros. This similarity index was contrasted with two types of shuffled controls: (1) within-shuffle, in which the neurons within a given Up-state were shuffled; and (2) between-shuffle, in which the same cell maintained its position but was shuffled between Up-states (Fig. 3A). Additionally, we performed clustering analysis on the mean ΔF/F over time of each cell in an Up-state. For this, the NxT matrix was collapsed across time, and each Up-state was represented by a vector of size N. We also performed principal component analysis (PCA) on the concatenated Up-states, and plotted the scores of the top three principal components. This analysis, however, was only used for visualization purposes (Fig. Supplement 2B,C).

To extract the time (latencies) of the Ca2+ trace peaks we used the findpeaks MATLAB function, and used the median of these peak times across all segmented cells within a slice and all ten light evoked test trials.

Optical stimulation

For the all-optical homeostatic plasticity experiments, ex vivo slices that co-expressed ChrimsonR and GCaMP6f were used. To reduce variability, control and experimental groups relied on "sister” slices, derived from the same batch of animals (littermates), maintained with the same culture medium and serum, placed in the same incubator and virally transfected in the same session. In each experiment, two slices (from the same animal) of each genotype (Fmr1+/y or Fmr1−/y) were placed in the “stimulating incubator” at 21–25 DIV (four slices from two littermate mice). One slice per genotype received chronic optical stimulation (COS) via a red LED (Super Bright LEDs, 630 nm wavelength) while the other was kept in the same incubator but did not receive COS. Optical stimulation consisted of a 50 ms flash of red light driven by two 1.5 V batteries and yielded an output of ~ 0.1 mW/mm2 delivered every 30 s for 3–4 days. Immediately following COS slices were transferred on their intact filters to a custom-built chamber on the stage of the 2P rig and Ca2+ imaging was performed at 25–30 DIV (Fig. 5A,B). For acute optical stimulation during Ca2+ imaging experiments, we used an external LED (Thorlabs 625 nm, M625L4) with a longpass filter (Thorlabs 600 nm, FEL0600) to deliver full-field optogenetic manipulation while minimizing light leakage into the green photomultiplier tube (Fig. Supplement 3). For Interval learning experiments, a similar stimulation protocol was used, however, the light delivery consisted of two pulses of 50 ms separated by 250 ms (short group) or by either 750 or 1,000 ms (long group) every 60 s for 24 h (Fig. 6A).

Figures

All figures plotted using box-and-whisker plots, box represents 25–75% (interquartile) percentile range, whiskers represent the range of the non-outlier data points. Outliers (squares) are those that fall 1.5 times the interquartile range above or below the box edges. The line within the box represents the median. ImageJ was used to create immunohistochemistry figures.

Statistics

All statistical analyses were done using MATLAB. Statistical tests for normality (Lilliefors test) were performed on each data set, and depending on whether the data significantly deviated from normality (p < 0.05) or did not deviate from normality (p > 0.05) appropriate non-parametric or parametric tests were performed. The statistical tests performed are mentioned in the text and the legends. Parametric analyses relied on students t-test and one- or two-way ANOVAs. The Mann–Whitney (RankSum function in MATLAB) was used for nonparametric comparisons. For the data in Figs. 3 and 4 the similarity indices were Fisher transformed for presentation and statistical tests.