Introduction

Wireless communication systems have gradually used innovative methods to meet the requirements of increased channel capacity and boost the transmission data-rate to develop communication applications. Conventional communication methods have faced the barriers of radio spectrum efficiency and the channel capacity expansion. One recently way to achieve higher capacities1 is to spatially multiplex multiple orthogonal modes using a single transmitter/receiver aperture pair, in which each mode carries an independent data stream. Orthogonality assures that the modes can be efficiently multiplexed at the transmitter, spatially co-propagated, and are demultiplexed at the receiver with minimal modal crosstalk2. As a new degree of freedom, due to the mutual orthogonality among eigenstates of the orbital angular momentum, scholars have conducted several versatile researches on the orbital angular momentum (OAM). Since then, beams carrying OAM inspires a new thinking in many diverse applications ranging from classical and quantum communication to optical manipulation3,4,5.

Similar to light beams, it is well-known that electromagnetic (EM) waves can carry both linear momentum (LM) and angular momentum (AM). The linear momentum of EM waves is associated with the Poynting’s vector. The angular momentum constitutes spin angular momentum (SAM) and orbital angular momentum (OAM)6 in the paraxial regime. The SAM defines the spin feature of photon and is associated with the polarization of the light and modes of EM waves. In the optical regime, it has only two value of \(\pm h\) (Plank’s constant divided by 2π) per photon. In electromagnetics, three possible polarization modes may be attributed to the electromagnetic beam, namely the left- and right-circularly polarized modes and linearly polarized mode. These modes merely impose channel limitation in communication systems. On the other hand, OAM defines the orbital rotation of photon. Each photon has an OAM of \(\,\pm lh\), where \(\,l\) is known as a topological charge or OAM index, which can be any integer ranging from \(-\infty \,\)to \(\infty \).

In 19927, Allen et al. first demonstrated that light beams with an azimuthal phase distribution \(\exp (il\varphi )\) carries an angular momentum independent of the polarization photon state, where \(\varphi \,\)is the azimuthal angle around the propagation axis and \(l\) is the topological charge, which represents the number of twists of the wavefront. Before that, Soskin et al. created a structured light with helical wavefront by using forked gratings8. It has been used to demonstrate high-capacity optical and radio communication channels by employing multiple OAM states into the transmitted EM wave on the light. In 2007 Bo Thide introduced the OAM concept from an optical frequency to a radio band by using circular array antennas with a gradient phase difference9.

At present, various methods for generating EM OAM waves have been presented. In optics, computer-generated holograms (CGH)10, spiral phase plates (SPP)11, spatial light modulators (SML)12 and Q-plate have been generated by the spin-orbit coupling in inhomogeneous media13. At radio domain, circular phase array antennas14,15, dielectric resonator antennas16, reflect and transmit arrays17,18 and metasurfaces19,20,21 have been designed. Although there are various designs in different configurations, the design principles for OAM generation lead to one universal rule: the introduction of the azimuthal phase term \(\exp (il\varphi )\) to EM waves.

By comparison with the conventional methods, owing to the extreme controls of EM waves, (namely low loss, low profile, low cost, and high performance), it has been proved that metasurfaces are more convenient to create versatile radiation beams22. Generally, metasurfaces, which are the planar version of bulky 3D metamaterials are divided into two categories including periodic and quasi-periodic structures. The first category is widely used in frequency selective structures23, polarization convertors24 and polarization rotators25. Meantime, much attention has been focused on the quasi-periodic structures, by reason of providing more design freedom to perform inhomogeneous surfaces. Various prototypes of radiators have been proposed for OAM generation, such as golden nanorods in26, L-shaped gold nanoantennas27, artificial perfect-electric and perfect-magnetic conductors anisotropic metasurface28, ultra-thin complementary metasurface aimed for double-layer complementary metasurface for OAM generation with high efficiency and metasurface Fork gratings29.

It is necessary to provide a more appropriate and efficient design procedure. The metasurfaces shaped by artificial impedance surfaces have many applications in designing leaky-wave antennas30. Surface wave leakage manipulation is one of the important applications of metasurface31. Wave leakage can be made by perturbation in the propagation medium. The great advantage of the leaky-wave systems is controlling the amplitude and propagation direction of the leaky waves32. Combining with the microwave holography principle, the desired wave can be generated by exciting the hologram interference of the reference wave and object wave in any desired direction33. The physical equivalence between the leaky waves and holographic antennas based on the Oliner’s method was given in34. The holography principle in optics was first introduced by Gabor35. Checcacci36 then utilized it at microwave frequencies. Since it has high potentials in various applications, research has been undertaken extensively on this theory. Sievenpiper37 proposed the hologram leaky wave for pattern synthetization. Periodic ground patches supporting \(T{M}_{0}\) surface wave are used to realize this concept. The new degree of freedom, which is the possibility of polarization manipulation has been added to hologram designs using anisotropic unit-cells38.

In this paper, we propose two different kinds of holographic leaky-wave metasurfaces to generate OAM modes with \(l=2\) and \(l=3\) at 18 GHz. The metasurfaces comprise of hexagonal patches on the grounded dielectric. We use the monopole antenna to excite the interferogram, which is the recorded interference of reference and object waves for the generation of the desired OAM beams.

The principle of holography for designing the leaky-wave metasurface

The evolution of the holography concept, which was indicated as a two-step imaging process, opened a new vision into wave phenomena and leading to development of a new class of antenna named holographic antenna39. It is important to explain the two-step imaging process, including the hologram formation and wave front reconstruction steps. Based on the microwave holographic theory, the reference wave excites the hologram and is consistent with the wave scattered from the object, which is called object wave. The intervention of the reference wave and object wave is called the interferogram pattern40. The desired radiation waves can be generated by exciting the hologram interference (generated by the reference wave and object wave). holographic leaky wave metasurfaces are assembled of quasi-periodic surface impedance. If (ψref) and (ψobj) define the reference wave and object waves, respectively, the surface impedance realizing the object wave is given by:

$${Z}_{s}=j{X}_{0}{\eta }_{0}(1+M\times {\mathcal R} \{{\psi }_{ref}{\psi }_{obj}^{\ast }\})$$
(1)

where \({X}_{0}\) is the normalized impedance with respect to the free space intrinsic impedance (\({\eta }_{0})\), \(M\) is the modulation depth coefficient, \( {\mathcal R} \) defines the real part of the \(({\psi }_{ref}{\psi }_{obj}^{\ast })\) and “*” denotes the complex conjugation operation. The reference wave may be selected as the surface or space wave. Here, for our proposed metasurfaces, the reference waves are defined as cylindrical waves in the form of Hankel function of the second kind:

$${\psi }_{ref}=\alpha {H}_{0}^{(2)}(\beta \sqrt{{x}^{2}+{y}^{2}})$$
(2)

where \(\beta \) is the phase constant for the \(T{M}_{0}\) surface mode and is obtained as

$$\beta ={k}_{0}\sqrt{1+{X}_{0}^{2}}$$
(3)

Observe that \(\beta \,\)is an approximation of the wave number which is applied for the object wave calculation and derivation of the associated surface impedance. The modulation factor (\(M)\) should be small value to justify the approximated value of \(\beta \). Otherwise, if the modulation depth is not small, the phase constant (\(\beta )\) may be obtained by the dispersion relation. The desired object wave (radiation wave) in this work in a specific direction is represented as:

$${\psi }_{obj}={e}^{-j(kxsin{\theta }_{0}cos{\varphi }_{0}+kysin{\theta }_{0}sin{\varphi }_{0}+l\phi )}$$
(4)

where \({\theta }_{0}\,\)and φ0 are the main lobe direction angles in the XZ and XY planes, respectively. \(l\) is the topological charge and defines the number of twists.

The schematics in Fig. 1 demonstrate the hologram principle and leaky wave theory to design the holographic leaky-wave metasurface. It illustrates that exciting the interferogram or holographic surface impedance by the reference wave, the object wave or desired radiation wave is generated.

Figure 1
figure 1

The schematic views of the cylindrical reference wave, object wave and interferogram.

Full size image

Higher-ordered bessel beam and orbital angular momentum

Non-diffracting Bessel beams are a set of solutions41 of the free space Helmholtz equation and have transverse intensity profiles that can be described by the Bessel function of the first kind. They have several features, such as non-diffraction, self-reconstruction, and even providing optical pulling forces. The scalar form of Bessel beams wave-function can be introduced as:

$$E(r,\varphi ,z)=A.\exp (i{k}_{z}z).{J}_{n}({k}_{r}r).\exp (\pm jn\varphi )$$
(5)

where \(\,A\) is the amplitude \(,\,{k}_{z}\,\)and \(\,{k}_{r}\) are the corresponding transverse and longitudinal propagation constants that satisfy the equation \(\sqrt{{k}_{z}^{2}+{k}_{r}^{2}}=k=2\pi /\lambda {\prime} \). It can be derived from Eq. (5) that the transverse intensity profiles of Bessel beams are independent of \(z\) coordinate which gives rise to their non-diffracting characteristic. Due to that OAM is structured beam with phase term \(\exp (il\varphi )\) and is related to vorticity and phase singularity it also shows that any higher-ordered Bessel beam \((n\ne 0)\) must carry an orbital angular momentum and have zero intensity along the \(z\) axis at \(r=0\) because of the phase singularity resulting from \(\exp (\pm jn\varphi )\) term.

The general form of the aperture field for the Bessel beams which carry an orbital angular momentum with the mode of \((n+1)\) can be defined as:

$$\overrightarrow{E}(r,\varphi ,z)=({E}_{r}\hat{r}+{E}_{\varphi }\hat{\varphi }+{E}_{z}\hat{z}).{e}^{-j{k}_{z}z}{e}^{-j(n+1)\varphi }$$
(6)

\({E}_{r}\), \({E}_{\varphi }\), and \({E}_{z}\) components are:

$$(\begin{array}{c}(-\,{C}_{TE}\frac{Jn({k}_{r}r)+Jn+2({k}_{r}r)}{2}+i.{C}_{TM}{e}^{in}\sqrt{1-N{A}^{2}}\frac{Jn({k}_{r}r)+Jn+2({k}_{r}r)}{2})\mathop{r}\limits^{\frown {}}\\ -({C}_{TM}{e}^{in}\sqrt{1-N{A}^{2}}\frac{Jn({k}_{r}r)+Jn+2({k}_{r}r)}{2}+i.{C}_{TE}\frac{Jn({k}_{r}r)+Jn+2({k}_{r}r)}{2})\mathop{\phi }\limits^{\frown {}}\\ NA.{C}_{TM}{e}^{in}\,{J}_{n+1}({k}_{r}r)\mathop{z}\limits^{\frown {}}\end{array})$$
(7)

where \({C}_{TM}\) and \(\,{C}_{TE}\,\)are complex numbers associated with the constituent transverse magnetic and transverse electric waves of Bessel beams; \(\eta \) is the phase difference between \({C}_{TM}\,\)and \(\,{C}_{TE}.\) The coefficient of \(NA\) shows the contribution of \(z\) component in the near field. For high NA Bessel beams, the electric field of the \(z\) component results from TM waves: the higher the NA, the higher the contribution the TM waves make to \({E}_{z}\). The \({E}_{r}\) and \({E}_{\varphi }\) components mainly result from TE wave contribution, as the term \(\sqrt{1-N{A}^{2}}\) is relatively small for the high NA case.

Now consider that the value of \({k}_{r}r\) is large enough, so the argument of Bessel function can be approximated as:

$${J}_{n}({k}_{r}r)\approx \sqrt{\frac{2}{\pi {k}_{r}r}}\,\cos \left({k}_{r}r-\frac{\pi }{4}-\frac{n\pi }{2}\right)$$
(8)

So \({J}_{n}({k}_{r}r)\) and \({J}_{n+2}({k}_{r}r)\) cancel each other due to a \(\pi \) phase difference, and the \(\varphi \) component of the aperture will be zero. These coefficients also have direct contributions in the far field pattern, and their effects will be canceled in the far field. As a result, in the far field approximation, by using isotropic unit-cells we can generate OAM modes.

Analysis of monopole launcher as a reference wave

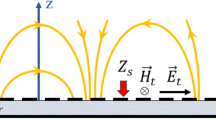
Choosing the proper reference wave is the crucial step of the design procedure of modulated metasurfaces. The monopole launcher on a grounded dielectric medium is selected for the excitation of \(T{M}_{0}\) surface waves. The electric and magnetic fields of the monopole launcher can be defined as42:

$${\overrightarrow{E}}_{sw}=\left[j{X}_{s}{J}_{sw}{H}_{1}^{(2)}({\beta }_{sw}\,\rho )\hat{\rho }+{J}_{sw}\frac{{\beta }_{sw}\,{\eta }_{0}}{{k}_{0}}{H}_{0}^{(2)}({\beta }_{sw}\,\rho )\hat{z}\right]{e}^{-{\alpha }_{z}z}$$
(9)
$${\overrightarrow{H}}_{sw}=-\,{J}_{sw}{H}_{1}^{(2)}({\beta }_{sw}\,\rho ){e}^{-{\alpha }_{z}z}\hat{\varphi }$$
(10)

where \({\beta }_{sw}\) and \({\alpha }_{z}\) are the radial propagation constant and the attenuation constant in the \(z\,\)direction, respectively. The radial propagation constant \({\beta }_{sw} > k\) obeys the dispersion equation:

$${\beta }_{sw}=k\sqrt{1+\overline{{X}_{s}^{2}}/{{\eta }_{0}}^{2}}$$
(11)
$${\alpha }_{z}=\sqrt{{\beta }_{sw}^{2}-{k}^{2}}=\frac{k}{{\eta }_{0}}\overline{{X}_{s}}$$
(12)

\({X}_{s}\) is the positive surface reactance of the grounded dielectric and TM-SW can be excited only if the reactance is positive.

It can be verified that the monopole launcher with moment \({I}_{0}\Delta {\rm{z}}\) have a relation with complex amplitude \(\,{J}_{sw}\) through:

$${J}_{sw}=-\,{I}_{0}\Delta {\rm{z}}\frac{{k}_{0}{\beta }_{sw}{X}_{s}}{2{\eta }_{0}}$$
(13)

The power transferred by the electric and magnetic fields is:

$$\begin{array}{c}{\overrightarrow{P}}_{SW}={\overrightarrow{E}}_{SW}\times {\overrightarrow{H}}_{SW}\ast =-\,jX{|{J}_{SW}|}^{2}{|{H}_{1}^{(2)}({\beta }_{SW}\rho )|}^{2}e-2{\alpha }_{z}z\mathop{z}\limits^{\frown {}}+\frac{{\eta }_{0}{\beta }_{SW}}{{k}_{0}}{|{J}_{SW}|}^{2}{H}_{0}^{(2)}\\ ({\beta }_{SW}\rho ){H}_{1}^{(2)}\ast ({\beta }_{SW}\rho )e-2{\alpha }_{z}{z}^{z}\hat{\rho }\sqrt{{b}^{2}-4ac}\end{array}$$
(14)

The Poynting’s vector along the \(\rho \) and \(z\) directions shows the coupling of waves to the dielectric medium. The power density cannot leave the dielectric43, and the propagation only occurs along the \(\rho \) direction, because the \(\hat{z}\) component of the Poynting’s vector is pure imaginary. The real part of the Poynting’s vector represents the propagation along the \(\rho \) direction. Also, only this part has a contribution to the holography Eq. (1).

Holographic design of leaky-wave metasurfaces for oam beams

Figure 2a,b show the 2-D holographic interference patterns of cylindrical surface wave and desired OAM beams with the topological charge of 2 and 3, respectively. The interference patterns are signified to generate desired object waves at the direction of \({\theta }_{0}\) = 0 and φ0 = 0. The color bar on the right shows the imaginary value of the patterns for the sample from minimum to maximum. These interferograms are extractions of the holographic equation of surface impedance (1) and the MATLAB software. For the constitution of surface impedances, it is all important that the dimensions of unit-cell be small relative to the wavelength. For the implementation of surface impedances, the grounded unit-cell patches (in the shape of square, circular, and hexagonal) are suitable.

Figure 2
figure 2

(a) The interference pattern of the reference wave and the object wave in direction \({\theta }_{0}\)= 0 and φ0 = 0 for OAM mode with topological charge 2. (b) The interference pattern of the reference wave and the object wave in direction \({\theta }_{0}\)= 0 and φ0 = 0 for OAM mode with topological charge 3.

Full size image

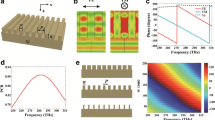
Considering the dispersion isotropy44, the hexagonal unit-cell is more well-behaved. Figure 3. represents the geometry of proposed unit-cell and its dispersion diagram in terms of different values of ap. It is notable that \(\beta \) have direct relation with surface impedance. The variations of the dispersion diagram represent the variations of surface impedance, moreover with changing the values of ap, the value of surface impedance changes. The value of a in Fig. 3 is 2.6 mm. The proposed method in45 is adopted to calculate the surface impedance.

Figure 3
figure 3

Geometry of the proposed unit cell and the dispersion diagram of the proposed unit-cell in terms of different values of ap.

Full size image

Figure 4 represents the curves of variations of imaginary parts of ηin and ηsurf at frequency 18 GHz as a function of the length of the hexagonal edge (ap). Figure 5 represents the equivalent transmission line circuit for the normal incident wave and TM mode. The surface impedance can be obtained by the conflation of the two models of transmission line in Fig. 5.

Figure 4
figure 4

The curves of variations of imaginary parts of ηin and ηsurf at frequency 18 GHz as a function of the length of the hexagonal edge (ap).

Full size image
Figure 5
figure 5

The equivalent transmission line of the proposed unit cell. (a) Normal incident model; (b) TM mode model.

Full size image

The input impedance, which is related to the reflection coefficient can be attained by a full wave simulation, which is associated with the reflection coefficient as:

$${\eta }_{in}={\eta }_{0}\frac{1+\Gamma }{1-\Gamma }$$
(15)

We can obtain the surface impedance for the normal incidence (ηsheet) which is shown in Fig. 5a with the aid of Eq. (16):

$$\frac{1}{{\eta }_{sheet}}=\frac{1}{{\eta }_{in}}-\frac{1}{j{\eta }_{1}\,\tan ({k}_{1}d)}$$
(16)

By using ηsheet, the surface impedance of the incident TM mode (ηsurf) may be obtained from the circuit in Fig. 5b:

$$\frac{1}{{\eta }_{surf}}=\frac{1}{{\eta }_{sheet}}+\frac{1}{j\frac{{\eta }_{0}k{z}_{1}}{{k}_{0}{\varepsilon }_{r1}}\,\tan (k{x}_{1}d)}$$
(17)

where:

$${k}_{{x}_{1}}=\sqrt{{k}_{0}^{2}({\varepsilon }_{r}-1)+{\left(\frac{{\eta }_{surf}{k}_{0}}{{\eta }_{0}}\right)}^{2}}$$
(18)

As the interference patterns shown in Fig. 2a,b, two different types of holographic leaky-wave antennas are proposed for the generation of OAM modes with topological charges of \(l=2\) and \(l=3\) operating at single frequency of 18 GHz in the direction of (\(\theta ={0}^{^\circ },\,\varphi ={0}^{^\circ })\), respectively. The substrate Rogers RO4003C is used in this work, which has a dielectric constant of \({\varepsilon }_{r}=3.55\), \(\,tan\delta =0.0027\), and thickness of 1.524 mm. The surface impedance (comprised of different sizes of hexagonal patches) is designed to produce the desired object waves. The values of M and X0 are arbitrary. However, their values should be selected in such a way that the impedance variation lies in the range of values obtainable by the synthesized unit-cells. Therefore, they are selected as X0 = 0.85 and M = 0.35. When the incident electromagnetic waves (reference wave) passes through the modulated metasurfaces, the desired radiation of OAM beams are generated.

Figure 6a,b depict the shapes of the centers of the metasurfaces. Due to that the desired object waves are different, the distinctive center of metasurfaces are observable according to the figures. Note that, the surface impedance depends on the incident and object waves.

Figure 6
figure 6

(a) The center of Holographic Leaky-wave metasurface for OAM mode \(l=2\). (b) The center of Holographic Leaky-wave metasurface for OAM mode \(l=3\).

Full size image

Determination of the aperture field approximation

The generalized form of the holographic theory is proposed for the synthesis of the anisotropic hologram using the aperture field approximation46. It is proposed in this paper that for the generation of the OAM beam of mode 1, the synthesis of anisotropic surface impedances is required by the aperture field approximation.

For the generation of OAM beams, the desired object wave is represented by \({\psi }_{obj}\) as an aperture electric field (\({\overrightarrow{E}}_{a})\):

$${\psi }_{obj}={\overrightarrow{E}}_{a}={e}^{-j(\overrightarrow{k}.\overrightarrow{r})-jl\mathop{\varphi }\limits^{ \acute{} }}\check{\rho }$$
(19)

If the aperture field is known, the antenna far-field may be calculated by47:

$$\overrightarrow{E}(r,\theta ,\varphi )=\frac{jk{e}^{-jkr}}{2\pi r}({F}_{\theta }(\theta ,\varphi )\hat{\theta }+{F}_{\varphi }(\theta ,\varphi )\hat{\varphi })$$
(20)

where \({F}_{\theta }(\theta ,\varphi )\) and \({F}_{\varphi }(\theta ,\varphi )\) are the Fourier transforms of aperture field.

$${F}_{\theta }(\theta ,\varphi )={f}_{x}\,\cos \,\varphi +{f}_{y}\,\sin \,\varphi $$
(21)
$${F}_{\varphi }(\theta ,\varphi )=\,\cos \,\theta ({f}_{y}\,\cos \,\varphi -{f}_{x}\,\sin \,\varphi )$$
(22)

where \({f}_{x}\) and \({f}_{y}\,\)are Fourier transforms of aperture field along the \(x\) and \(y\) axes, respectively obtained as:

$${f}_{x}({k}_{x},{k}_{y})=\int {E}_{ax}(\mathop{x}\limits^{ \acute{} },\mathop{y}\limits^{ \acute{} },\mathop{z}\limits^{ \acute{} }=0){e}^{j({k}_{x}\mathop{x}\limits^{ \acute{} }+{k}_{y}\mathop{y)}\limits^{ \acute{} }}d\mathop{x}\limits^{ \acute{} }d\mathop{y}\limits^{ \acute{} }$$
(23)
$${f}_{y}({k}_{x},{k}_{y})=\int {E}_{ay}(\mathop{x}\limits^{ \acute{} },\mathop{y}\limits^{ \acute{} },\mathop{z}\limits^{ \acute{} }=0){e}^{j({k}_{x}\mathop{x}\limits^{ \acute{} }+{k}_{y}\mathop{y)}\limits^{ \acute{} }}d\mathop{x}\limits^{ \acute{} }d\mathop{y\,}\limits^{ \acute{} }\,$$
(24)

where Eax and Eay are the aperture field components in the Cartesian coordinate axes, which may be obtained by decomposing \(\,\check{\rho }=cos\mathop{\varphi }\limits^{ \acute{} }\check{x}+sin\mathop{\varphi }\limits^{ \acute{} }\,\check{y}\), so:

$${\overrightarrow{E}}_{a}={e}^{-j(\overrightarrow{k}.\overrightarrow{r})-jl\mathop{\varphi }\limits^{ \acute{} }}\check{\rho }={e}^{-j(\overrightarrow{k}.\overrightarrow{r})-jl\mathop{\varphi }\limits^{ \acute{} }}(cos\mathop{\varphi }\limits^{ \acute{} }\check{x}+\,sin\mathop{\varphi }\limits^{ \acute{} }\,\check{y})$$
(25)

Substitute \(\,\mathop{x}\limits^{ \acute{} }=\,\mathop{\rho \,}\limits^{ \acute{} }cos\mathop{\varphi \,}\limits^{ \acute{} }\), \(\mathop{y}\limits^{ \acute{} }=\,\mathop{\rho \,}\limits^{ \acute{} }\,sin\mathop{\varphi ,}\limits^{ \acute{} }\,{k}_{x}={k}_{0}sin\theta \,\cos \,\varphi \) and \({k}_{y}={k}_{0}sin\theta sin\varphi \) into Eq. (25) to get:

$${E}_{ax}={e}^{-j{k}_{0}\mathop{\rho }\limits^{ \acute{} }sin{\theta }_{0}\cos (\mathop{\varphi }\limits^{ \acute{} }-{\varphi }_{0})-jl\mathop{\varphi }\limits^{ \acute{} }}cos\mathop{\varphi }\limits^{ \acute{} }\check{x}$$
(26)
$${E}_{ay}={e}^{-j{k}_{0}\mathop{\rho }\limits^{ \acute{} }sin{\theta }_{0}\cos (\mathop{\varphi }\limits^{ \acute{} }-{\varphi }_{0})-jl\mathop{\varphi }\limits^{ \acute{} }}sin\mathop{\varphi }\limits^{ \acute{} }\,\check{y}$$
(27)

Also,

$${k}_{x}\mathop{x}\limits^{ \acute{} }+{k}_{y}\mathop{y\,=\,}\limits^{ \acute{} }{k}_{0}sin\theta \,\cos \,\varphi \mathop{\rho \,}\limits^{ \acute{} }cos\mathop{\varphi }\limits^{ \acute{} }+{k}_{0}sin\theta sin\varphi \mathop{\rho \,}\limits^{ \acute{} }\,sin\mathop{\varphi }\limits^{ \acute{} }=\,{k}_{0}\mathop{\rho \,}\limits^{ \acute{} }sin\theta \,\cos (\mathop{\varphi }\limits^{ \acute{} }-\,\varphi )$$
(28)

By inserting Eqs. (26), (27) and (28) into Eq. (23) and (24):

$${f}_{x}={\int }_{0}^{2\pi }{\int }_{0}^{a}\cos \,\varphi {\prime} {e}^{jk}0\rho {\prime} (\sin \,\theta \,\cos (\varphi {\prime} -\varphi )-\,\sin \,{\theta }_{0}\,\cos (\varphi {\prime} -\varphi )).{e}^{-jl\varphi }\rho {\prime} d\rho {\prime} d\varphi {\prime} $$
(29)
$${f}_{y}={\int }_{0}^{2\pi }{\int }_{0}^{a}\sin \,\varphi {\prime} {e}^{jk}0\rho {\prime} (\sin \,\theta \,\cos (\varphi {\prime} -\varphi )-\,\sin \,{\theta }_{0}\,\cos (\varphi {\prime} -\varphi )).{e}^{-jl\varphi }\rho {\prime} d\rho {\prime} d\varphi {\prime} $$
(30)

By substituting Eqs. (29) and (30) into Eqs. (21) and (22):

$${F}_{\theta }=\,\iint \,\cos (\mathop{\varphi }\limits^{ \acute{} }-\,\varphi )\,{e}^{j{k}_{0}\mathop{\rho }\limits^{ \acute{} }(sin\theta \cos (\mathop{\varphi }\limits^{ \acute{} }-\varphi )-sin{\theta }_{0}\cos (\mathop{\varphi }\limits^{ \acute{} }-{\varphi }_{0}))}.\,{e}^{-jl\mathop{\varphi }\limits^{ \acute{} }}\mathop{\rho \,}\limits^{ \acute{} }d\mathop{\rho \,}\limits^{ \acute{} }d\mathop{\varphi }\limits^{ \acute{} }$$
(31)
$${F}_{\varphi }=\iint sin(\mathop{\varphi }\limits^{ \acute{} }-\,\varphi )\,{e}^{j{k}_{0}\mathop{\rho }\limits^{ \acute{} }(sin\theta \cos (\mathop{\varphi }\limits^{ \acute{} }-\varphi )-sin{\theta }_{0}\cos (\mathop{\varphi }\limits^{ \acute{} }-{\varphi }_{0}))}.\,{e}^{-jl\mathop{\varphi }\limits^{ \acute{} }}\mathop{\rho \,}\limits^{ \acute{} }d\mathop{\rho \,}\limits^{ \acute{} }d\mathop{\varphi }\limits^{ \acute{} }$$
(32)

Consequently, for the isotropic structure with \(\,{\rm{l}}=1\), the polarization is circular since \({F}_{\varphi }=(-j){F}_{\theta }\). However, due to \({F}_{\varphi }\& \,{F}_{\theta }\,\ne 0\), there is no null in the pattern. Note that one of the main characteristics of the OAM beams is the existence of a null and phase singularity in the pattern. Therefore, for the generation of topological charge \(l=1\), we need to synthesize an anisotropic surface impedance.

Experimental results

As Fig. 7a,b demonstrate, the proposed holographic leaky-wave metasurfaces with different OAM modes of \(l=2\) and \(l=3\) are fabricated by using PCB technology. To vindicate our approach, the fabricated metasurfaces are measured in an anechoic chamber as shown in Fig. 8a,b. The aperture size of both metasurfaces are similar as D = 117.75 mm. Each element has a hexagonal lattice with a period of 2.6 mm. It is mentionable that, the distance between the unit-cells are a pivotal value for reducing the return loss (\({S}_{11})\). Also, in order to avoid spurious radiation, the hexagonal patches around the launcher are removed. Furthermore, each metasurfaces have the identical circular apertures located at the center of them. For generating reference waves, exciting the metasurfaces and impedance matching, it is essential to solder the SMA connectors behind the structures and pass them through the circular apertures. The length of the monopole was selected to be 6.724 mm (0.4 \(\lambda \) at 18 GHz). Also, the simulations are done through CST and HFSS software by the Computer System characteristics of: CPU Corei7 6800 K/RAM: 64 GByte/Num. of Thread: 12/Num. of Cores: 6. The Figs. 9 and 10 show the simulation and measured reflection coefficients. The figures show that the simulated and measured values of S-parameters \({S}_{11}\) are below −10 dB ranges from 17 GHz to 19 GHz.

Figure 7
figure 7

(a) The fabricated holographic leaky-wave metasurfaces with topological charges of OAM of \(l=2\). (b) The fabricated holographic leaky-wave metasurfaces with topological charge of OAM of \(l=3\).

Full size image
Figure 8
figure 8

Experimental set-up of the proposed metasurfaces with topological charge of (a) \(l=2\,\) (b) \(\,l=3\).

Full size image
Figure 9
figure 9

The simulation and measurement results for the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=2\).

Full size image
Figure 10
figure 10

The simulation and measurement results for the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=3\).

Full size image

To study the far-field radiation behavior, a standard horn antenna is located 6.5 m away from the metasurfaces. Figure 11 show the simulated 3D far-field radiation pattern. Figures 12 and 13 show the simulated and measured Cartesian and polar patterns for the OAM modes. As the polar and Cartesian patterns show, there are zero depths in the desired direction, which are in accordance with the properties and features of EM OAM beams.

Figure 11
figure 11

3D far-field radiation patterns. (a) 3D far-field radiation pattern for OAM mode with \(l=2\). (b) 3D far-field radiation pattern for OAM mode with \(l=3\).

Full size image
Figure 12
figure 12

Simulated and measured patterns. (a) Simulated and measured Cartesian patterns for OAM mode with \(l=2.\) (b) Simulated and measured polar patterns for OAM mode with \(l=2\).

Full size image
Figure 13
figure 13

Simulated and Measured patterns. (a) Simulated and measured Cartesian patterns for OAM mode with \(l=3\). (b) Simulated and measurements polar patterns for OAM mode with \(l=3\).

Full size image

According to Fig. 13, the reason for the discrepancy between the simulation results and measurement data of the far-field pattern for the OAM mode 3, could be attributed to the imprecision of fabrication processes of metasurfaces in our laboratory. Also, the measurement equipment may not have been calibrated properly for the higher order OAM modes. Note that the resolution and dimensions of the unit-cells are the limitations for synthesizing the impedance surface pattern for generating the higher order OAM modes. Also, due to the mentioned difficulties and limitations the far-filed pattern of mode 3 is somewhat not symmetrical.

To verify the unique properties and features of the OAM beams, the intensity and phi-phase pattern of metasurfaces are obtained with simulations through CST and HFSS. By exporting the far-field data from the CST and HFSS and importing them to MATLAB, the data for Fig. 14 are extracted and drawn. For the figures depicting the field strength, the plots of the magnitude and phase of the far-field are drawn. Note that the vertical and the horizontal axes are in terms of u = \(sin\theta cos\varphi \) and \(v=\,sin\theta sin\varphi \), respectively.

Figure 14
figure 14

(a,b) The demonstration of CST and HFSS Simulation Phi-phase pattern of the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=2\,\),respectively (c,d)) The demonstration of CST and HFSS Simulation Phi-phase pattern of the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=3\), respectively (e) The demonstration of CST simulation of intensity pattern of the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=2\) and \(l=3.\) (f,g) The demonstration of HFSS simulation of intensity pattern of the holographic leaky-wave metasurfaces with topological charges of OAM of \(l=2\) and \(l=3,\) respectively.

Full size image

The Fig. 14 show the phi-phase and transverse intensity pattern of the OAM beams. Observe that a clear doughnut-shaped intensity pattern appears with a singularity in the center, and a spiral-shaped phase figures show that our proposed metasurfaces significantly generate OAM modes. Also, Fig. 14f,g represent the depth of the nulls in the intensity patterns for modes of \(l=2\) and \(l=3\), where the depth of the nulls are compliance with the Figs. 12a and 13a.

Conclusion

We have successfully demonstrated two different leaky-wave metasurfaces for the generation of OAM beams. The leaky wave theory and the microwave holography method were combined to attain the interference pattern. The proposed holographic leaky-wave metasurfaces comprise of hexagonal patches which have variation in their sizes and dimensions. The patches are suitable for any direction of incident waves. We have also performed computer simulations and conducted measurements for the fabricated metasurfaces. The simulation results were in good agreement with those of experimental measurements, which strongly demonstrated the excellent performance of our design. Due to their ultralow profile, low cost, compact structure and small size and easy fabrication and integration, these metasurfaces are expected to be an effective solution for the OAM mode generations.