Introduction

Two-dimensional (2D) layered systems, having nano-scaled thickness and unique geometric symmetries, have found themselves in the main stream of material sciences especially after the success of graphene. These novel materials have been found to possess critical applications due to their transport and optical properties. Other 2D layered structures include silicene1, germanene2, boron nitride (BN)3, gallium nitride (GaN)4, transition-metal dichalcogenides (TMDs)5, and stanene6,7. However, these materials have their own shortcomings. For example, graphene, silicene, germanene and stanene these group IV materials lack significant energy gaps and do not have sufficiently high on-off ratios for electronic applications8. TMDs display reasonable on-off ratios, but their carrier mobilities are usually relatively low (mostly lower than 100 cm2 V−1·s−1)9. In other words, the adequate on-off ratio and high carrier mobility hardly appear in these materials simultaneously. On the other hand, V-group elements have been attracting a considerable amount of attention due to their moderate band gap and carrier mobility. Among these elements, few-layer black phosphorus (phosphorene) has been fabricated successfully by using mechanical cleavage10,11, liquid exfoliation12,13, and mineralizer-assisted short-way transport reaction14,15.

The intrinsic energy gap in phosphorene ranges from 0.5 to 2 eV depending on the number of layers16,17,18, as demonstrated by optical measurements10,19. Such a gap is larger than that in its bulk counterpart (~0.3 eV)16,20,21. Phosphorene-based field-effect transistor has an adequate on/off ratio of 105 and a high carrier mobility of 103 cm2/V.s at room temperature20,22,23. Additionally, the unusual energy spectra and quantum Hall effect (QHE) due to magnetic quantization23,24,25,26,27,28,29,30,31,32, make few-layer phosphorene a very good candidate for being a next-generation electronic device33,34,35.

A layer of phosphorene presents a puckered structure owing to the sp3 hybridization of (3s,3px,3py,3pz) orbitals. The deformed hexagonal lattice in the x-y plane is a large contrast to the highly symmetric honeycomb lattice of the group-IV systems36. This unique geometric structure causes the highly anisotropic low-lying energy bands, i.e., the linear and parabolic dispersions near the Fermi energy EF, respectively, along the \(\widehat{{k}_{x}}\) and \(\widehat{{k}_{y}}\) directions17. The anisotropy clearly reveals in other physical properties, like the recent measurements of the optical and transport properties20,37,38. This gives extra advantages for phosphorene in comparison with MoS2- and related semiconductors. For example, the unusual anisotropy could be utilized in designing unconventional thermoelectric devices. That is, a thermal gradient and a potential difference could be put on in two orthogonal directions, producing the higher thermal conductivity in one direction and the larger electrical conductivity in another39,40. The special intrinsic property will directly reflect in quantization phenomena.

The recent experimental and theoretical researches indicate that graphene and -related systems have rich and unique quantum transport properties. Especially, the magnetic transport measurements of monolayer graphene present the unconventional half-integer Hall conductivity σxy = 4(m + 1/2)e2/h, where m is an integer and the factor of 4 is present due to spin and sublattice degeneracy. The n = 0 Landau level (LL), corresponding to the Dirac point, is mainly attributed to the quantum anomaly. For AB-stacked bilayer graphene, the Hall conductivity is in the form of σxy = 4m′e2/h (m′ a non-zero integer). However, an exception is a double step of σxy = 8e2/h at zero energy and low magnetic field41. This corresponds to the degeneracy of the n = 0 and n = 1 LLs of the first group42. The unusual phenomena of electronic transport properties of graphene stimulate a lot of interest in exploring the configuration-enriched QHE in other novel 2D materials.

In this paper, we utilize the generalized tight-binding model and the Kubo formula under the linear response approximation to investigate the unusual QHE of bilayer phosphorene. The effects of the geometrical structures, intrinsic interactions, electric field Ez and magnetic field Bz are considered simultaneously. Such method is capable of identifying the magneto-electronic selection rules in the static limit and obtaining the available transition channels in the magneto-transport properties. The relations of quantum conductivity with the Fermi energy EF, Ez and Bz are discussed in detail. They are closely related to the electronic structure, the LLs, and the transition channels.

Changing the electric field strength can greatly diversify the magnetic quantization and enrich the transport properties. The various features could cover half-integer and integer conductivities with distinct steps, a vanishing or non-zero conductivity at the neutral point, and the well-like, staircase, composite, and anomalous plateau structures in the field dependencies. The frequent anticrossing/crossing behaviors of two-groups of LLs may be responsible for the unusual field-dependent characteristics. This illustrates that the feature-rich LLs can create extraordinary magneto-transport properties.

Methods

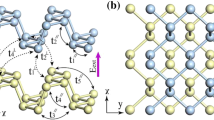
Monolayer phosphorene, with a puckered honeycomb structure, has a primitive unit cell containing four phosphorous atoms, as depicted by the dashed yellow lines in Fig. 1(a). Two of the four phosphorous atoms are located on the lower (the red circles) or higher (the green circles) sublattice sites. Similar structures are revealed in few-layer systems, e.g, bilayer phosphorene as shown in Fig. 1(b) for AB stacking. The low-lying energy bands are dominated by the interactions between the 3pz orbitals17. The few-layer Hamiltonian is represented by

$$H=\mathop{\sum }\limits_{i\mathrm{=1,}l}^{4}({\varepsilon }_{i}^{l}+{U}_{i}^{l}){c}_{i}^{l}{c}_{i}^{\dagger \,l}+\sum _{\langle i,j\rangle ,l}{h}_{ij}^{ll}{c}_{i}^{l}{c}_{j}^{\dagger \,l}+\sum _{\langle i,j\rangle ,l\ne {l}^{\text{'}}}h{\text{'}}_{ij}^{l{l}^{\text{'}}}{c}_{i}^{l}{c}_{j}^{\dagger \,{l}^{\text{'}}},$$
(1)

where i and l represent the atom and layer numbers, respectively. \({\varepsilon }_{i}^{l}\) is zero in a monolayer, but for a few-layer system, it is a layer- and sublattice-dependent site energy due to the chemical environment. Also, \({U}_{i}^{l}\) is the Coulomb potential energy induced by an electric field. They both contribute to the diagonal matrix elements. In the absence of a magnetic field, the summation is written as \({\Sigma }_{i\mathrm{=1,}l}^{4}\), but in the presence of a magnetic field it becomes \({\Sigma }_{i\mathrm{=1,}l}^{4{R}_{B}}\) (seen later). Also, \({c}_{i}^{l}\) (\({c}_{j}^{\dagger \,{l}^{\text{'}}}\)) is an annihilation (creation) operator, \({h}_{ij}^{ll}\) and \({h}_{ij}^{\text{'}\,l{l}^{\text{'}}}\) are, respectively, the intralayer and interlayer hopping integrals, and the effective interactions used in the calculations cover the fourth and fifth neighboring atoms. These hopping parameters have been adopted from ref. 17.

Figure 1
figure 1

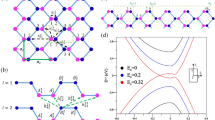
The top view for the geometric structure of monolayer phosphorene in (a), and the side view for that of bilayer phosphorene in (b), with various intralayer and interlayer atomic interactions. In the presence of a uniform perpendicular magnetic field, an enlarged unit cell is in rectangular shape as shown in (c) by the dashed green lines. The band structures of bilayer phosphorene under various electric fields are presented in (d).

Full size image

Black phosphorene is assumed to be in the presence of a uniform perpendicular magnetic field. The magnetic flux through a unit cell is \(\Phi ={a}_{1}{a}_{2}{B}_{z}\), where a1 = 3.27 Å and a2 = 4.43 Å are lattice constants (the lattice vectors are shown as the yellow arrows in Fig. 1(a)). The vector potential, \(\overrightarrow{A}=({B}_{z}x)\hat{y}\), creates an extra magnetic Peierls phase of \(\exp \{i[\frac{2\pi }{{\phi }_{0}}\int \overrightarrow{A}\cdot d\overrightarrow{r}]\}\), leading to a new period along \(\hat{x}\) and thus an enlarged rectangular unit cell with \(4{R}_{B}=4{\phi }_{0}\,/\Phi \) atoms in one layer, as illustrated in Fig. 1(c). Here, ϕ0 (\(=\,h/e=4.1\times {10}^{-15}\) T·m2) is the magnetic flux quantum; ϕ0/Φ is chosen to be an integer. The reduced first Brilloun zone has an area of \(4{\pi }^{2}\,/{a}_{1}{a}_{2}{R}_{B}\). For bilayer black phosphorous, the magnetic Hamiltonian matrix is very large with 8RB × 8RB matrix elements within achievable experimental field strengths, e.g., the dimension of 16800 at Bz = 30 T. The details of the matrix elements can be seen in the Supplementary Information.

The spatial distributions of subenvelope functions derived from the generalized tight-binding model are utilized to characterize the magnetic quantum numbers and the types of LLs43,44,45. They are useful for explaining the peculiar LL behaviors. For example, the quantum number and subgroup classification can be determined by the number of zero points and the dominant sublattices. This enables us to identify the magneto-electronic selection rules in the static limit and obtain the available transition channels in the magnetotransport. The numerically intensive procedure is not restricted to the geometric structure, the number of layers, the stacking order, and the type of external fields. To achieve the experimentally attainable field strengths, a band-like matrix has been developed to solve the huge matrix efficiently46. Accordingly, we can observe the strong electrically-tunable LL spectra when Bz < 60 T.

The magnetically quantized LLs can create unique transport properties. Within linear response theory, the transverse Hall conductivity is evaluated from the Kubo formula47:

$${\sigma }_{xy}=\frac{i{e}^{2}\hslash }{S}\sum _{\alpha \ne \beta }({f}_{\alpha }-{f}_{\beta })\frac{\langle \alpha |{\dot{{\bf{u}}}}_{{\bf{x}}}|\beta \rangle \langle \beta |{\dot{{\bf{u}}}}_{{\bf{y}}}|\alpha \rangle }{{({E}_{\alpha }-{E}_{\beta })}^{2}}\mathrm{}.$$
(2)

here, |α〉 is a LL state with energy Eα, S the area of the enlarged unit cell, fα,β the Fermi-Dirac distribution functions, and \({\dot{{\bf{u}}}}_{{\bf{x}}}\) (\({\dot{{\bf{u}}}}_{{\bf{y}}}\)) the velocity operator along \(\hat{x}\) (\(\hat{y}\)). The matrix elements of the velocity operators, which determine the permitted inter-LL transitions, are evaluated by the gradient approximation48:

$$\begin{array}{c}\langle \alpha |{\dot{{\bf{u}}}}_{{\bf{x}}}|\beta \rangle =\frac{1}{\hslash }\langle \alpha |\frac{\partial H}{\partial {k}_{x}}|\beta \rangle ,\\ \langle \alpha |{\dot{{\bf{u}}}}_{{\bf{y}}}|\beta \rangle =\frac{1}{\hslash }\langle \alpha |\frac{\partial H}{\partial {k}_{y}}|\beta \rangle \mathrm{}.\end{array}$$
(3)

The above procedure promises the self-conserved number of carriers per area with and without a magnetic field. Since the intra-layer and inter-layer atomic interactions, and the effects of external fields are simultaneously included in the Hamiltonian matrix, the results are accurate and reliable within a wide energy range. The correct LL spectrum and wavefunctions are used for characterizing subgroups of LLs at low energies. The strong competition between them induces the unusual quantization behaviors, such as the frequent anticrossings for the Bz- and Ez-dependent energy spectra. This brings about the anomalous quantum Hall conductivities. These critical characteristics are either missed or not explained in other papers that use the effective-mass model49,50, or consider a one-dimensional ribbon25,26,31,51. In ribbons, the quantum confinement would hinder the magnetic quantization leading to partially dispersionless energy spectra52 rather than the dispersionless LLs in a two-dimensional system43,44,45. Our method warrants more reliable results on QHE for an arbitrary Fermi level and external field strength.

Results and discussion

The special lattice structure and complex hopping integrals generate rich band structures. Bilayer black phosphorous (BP) has a direct gap of Eg ≈ 1 eV near the Γ point, as illustrated in Fig. 1(d) by the black curves. The highly anisotropic energy bands yield the approximately linear and parabolic dispersions along ΓX and ΓY (\({\hat{k}}_{x}\) and \({\hat{k}}_{y}\)), respectively. An electric field Ez could reduce the energy gap considerably. The semiconductor-semimetal transition appears at a strength larger than \({E}_{z,c}\simeq 0.3\) (eV/Å; blue curves), for which the valence and conduction bands are transformed into linearly intersecting bands and oscillatory bands along ΓY and ΓX, respectively, highlighted in the upper inset. The Dirac semimetal state, created by the Ez field, was directly observed by angle-resolved photoemission spectroscopy (ARPES) in bulk53 and few-layer BP54. The extreme points remain at the Γ point. Two Dirac points (saddle points) are situated on both sides of the Γ point along \(+{\hat{k}}_{y}\) and \(-{\hat{k}}_{y}\) (\(+{\hat{k}}_{x}\) and \(-{\hat{k}}_{x}\)). Especially, two constant-energy loops, inner and outer, surround the Γ point in the region between the extreme and saddle point energies. This is illustrated by the contour plot for Ec = 0.04 eV in the lower inset. The strongly tunable electronic structure is predicted to bring about peculiar optical55 and transport56 properties. The electronic states near the Dirac and Γ points are magnetically quantized into two distinct LL subgroups. The hybridization of the two subgroups reaches a maximum at the saddle point energy (\({E}^{c}\approx 0.028\) eV; \({E}^{v}\approx -\,0.035\) eV), which could cause anomalous magneto-optical57 and -transport properties. It is noted that the Ez effects on the lowest pair of energy bands at the Γ point are qualitatively similar for various layer numbers58,59. The different features in the energy bands between them may occur at the other symmetric points and higher energies. This would require the multi-orbital TB calculations44,60, for further study.

All the critical points and constant-energy loops in the energy-wave vector space will dominate the main features of the LLs. For \({E}_{z} < {E}_{z,c}\) (Fig. 2(a,b)), the states around the Γ point contribute to the low-lying LLs, which are four-fold degenerate for each (\({k}_{x},{k}_{y}\)) state including spin and localization-center degeneracies. The occupied LLs are not symmetrically located with respect to the unoccupied ones near the Fermi level. The quantum number nc (nv) for each conduction (valence) LL is clearly identified from the number of zero nodes in the wavefunctions. For example, the four low-lying conduction/valence LLs have nc,v = 0, 1, 2; 3. Though they have well-behaved Bz-dependence, their energies cannot be well described by a simple relation especially for higher energy and field strength. This is different from the square-root dependence in monolayer graphene61, and the linear dependence in AB-stacked bilayer graphene42 and MoS262, due to the highly anisotropic energy dispersion.

Figure 2
figure 2

(a–c) The Bz-dependent LL spectra for various Ez’s and (d) the Ez-dependent LL spectrum at Bz = 30 T.

Full size image

A modest value for Ez would lower (raise) the lowest unoccupied LL (highest occupied LL) energy, as shown in Fig. 2(b). The drastic changes in the LL spectrum come about when Ez is increased to over Ez,c (Fig. 2(c)). First, the lowest unoccupied and the highest occupied LLs merge together due to the zero band gap. Then, the low-lying LLs evolve into two groups around EF. The lower one, namely the D-group with double degeneracy, could be fitted by a square-root relation \(\sqrt{{n}_{D}{B}_{z}}\). That corresponds to the magnetic quantization of electronic states near the two Dirac points, similar to graphene61. For the higher one, the Γ-group, beginning at the band-edge-state energies at Γ point (indicated by the blue arrows), the level energies are inversely proportional to Ez. Γ-group LLs with their own set of quantum numbers nΓ are associated with the inner constant-energy loops (see the lower inset of Fig. 1(d)) and frequently cross the LLs from the outer loops. Γ- and D-group LLs have strong hybridizations around the saddle point energies, indicated by the green arrows, where they cross and anticross each other alternatively. The anticrossings clearly illustrate that such LLs are composed of multi-oscillation modes43,63,64. It is worth noting that the two subgroups of LLs will finally evolve into one at the larger Bz’s, as shown in the Supplementary Information.

The strong electrically-tunable LL spectrum is demonstrated in Fig. 2(d) for Bz = 30 T. The zero-energy LL is generated at .. The larger nc,v requires the stronger Ez to form the D-group LL. That is, two entangled LLs gradually merge together with increasing Ez. Above the region, one sees that Γ-group LLs are formed beyond the turning points (the first turning point is indicated by the green arrow). The energies of Γ-group LLs increase with Ez quickly. This distinguishes them from the other LLs coming from the outer constant-energy loops. Clearly, the feature-rich LL spectrum strongly depends on the energy regime as well as strengths of the external field. This could result in interesting magneto-transport properties.

The dependence of the Hall conductivity on the Fermi energy is very sensitive to Ez, as exhibited in Fig. 3(a) through 3(d) for Bz = 30 T. When Ez = 0 (Fig. 3(a)), the conductivity is quantized as \({\sigma }_{xy}=2m{e}^{2}/h\) (where m is an integer) with almost equal plateau widths. This reflects the parabolic energy dispersion at Bz = 0. For the intrinsic state, only interband inter-LL transitions are allowed. The peak intensities and selection rules for the intrinsic magneto-optical spectra are strongly anisotropic57. That is, the selection rules for the x- and y-polarizations are Δn = odd and even numbers, respectively. Since the transverse electric conductivity σxy is related to the product of velocity matrix elements along the two directions (Eq. (2)), it becomes zero with the distinct selection rules, leading to a wide zero plateau centering around zero energy. This is different from the case in graphene, where the available interband inter-LL transition channels Δn = 1 and Δn = −1, respectively, possess opposite contributions to σxy and cancel each other65. The intraband inter-LL transitions determine the magnitude of σxy. That is, when EF is between the nc = n − 1 and nc = n LLs (n is a positive integer), the transition between the two LLs mainly contributes to σxy = + n (in units of 2e2/h), while EF between nv = n − 1 and nv = n LLs it leads to σxy = −n. Thus, varying EF/passing the LLs (shown in the upper inset) makes the step structures. The width of the zero-conductivity plateau can be reduced by Ez considerably, while for a modest value of Ez the quantization relation σxy = 2me2/h remains (Fig. 3(b)). It is until Ez > Ez,c that σxy displays distinct features, like in Fig. 3(c) for Ez = 0.32. There are three main characteristics. First of all, the plateau of σxy = 0 disappears, which is attributed to the creation of zero-energy LL. Secondly, around EF = 0 the quantized values of the Hall conductivity are changed from integer to half-integer with the double level degeneracy, i.e., from σxy = 2me2/h to σxy = 4(m′ + 1/2)e2/h (m′ a nonzero integer). This manifests the formation of D-group LLs. Thirdly, there exist a few of very narrow plateaus, as indicated by the green arrows. They arise from the lift of LL degeneracy or the appearances of Γ-group LLs (the purple line in the upper inset). Figure 3(d) displays the region of further lower EF. It demonstrates that the coexistence of two groups of LLs could induce the nonuniform plateau widths. However, when EF becomes smaller than the extreme-point energy at Γ point (≈ −0.053 eV), the structures turn monotonous, i.e, they obey the relation σxy = 2me2/h. The regular quantization means that the LLs originating from the outer constant-energy loops (see the lower inset of Fig. 1(d)) become dominant.

Figure 3
figure 3

The EF-dependent transverse conductivity at Bz = 30 T for (a) Ez = 0, (b) Ez = 0.29, and (c) Ez = 0.32 eV/Å. Also shown in (d) is the lower energy region for Ez = 0.32 eV/Å. The upper inset in each panel shows the corresponding LL energies.

Full size image

The Bz-dependent Hall conductivity exhibits a variety of features when Ez is varied, as shown in Fig. 4(a–d). These characteristics are due to the behavior of the LL energy spectrum as a function of magnetic field seen in the insets of each panels. For Ez < Ez,c (Fig. 4(a)), strengthening Bz decreases the quantum number of the highest occupied LL and increases the inter-LL spacing of the dominant transition channel around EF (the dashed green line). Consequently, the height/width of the Hall plateau is reduced/broadened when passing through a LL. This is in marked contrast to the case shown in Fig. 3(a,b) where varying EF barely changes the plateau width. The value of σxy drops to zero over a critical strength Bz,c (not shown). The larger the value of EF is, the stronger strength of Bz,c is required. As for Ez > Ez,c, we observe that there are three main types of σxy-Bz dependencies for chosen EF, as displayed in Fig. 4(b) through 4(d). Firstly, when EF is located in the linear energy region (the inset in Fig. 4(b)), the conductivity exhibits the half-integer QHE in units of 4e2/h. There is a narrow plateau at Bz ≈ 36 T due to a pair of entangled \({n}_{D}^{c}=1\) LLs. σxy does not achieve the zero value because of the existence of a zero energy LL. Secondly, EF between in the energies of extreme and saddle points as shown in the inset of Fig. 4(c), where two groups of LLs coexist, the conductivity possesses a composite quantum structure. The reason of this is that the intra inter-LL transitions of D- and Γ-group LLs contribute to positive and negative σxy, respectively. Therefore, with decreased quantum numbers of D-/Γ-group LLs, the value of σxy is reduced/increased. This results in the unusual structures for certain strengths of Bz, including the double-width plateau (the red rectangle), bulging (the yellow rectangle) and dip (the green rectangle) structures. The first kind of structure happens when EF is located at a LL crossing point exactly, while the latter two occur when EF is slightly above and below a LL crossing point, respectively. Lastly, when EF is higher than the band-edge-state energy at the Γ point (Fig. 4(d)), the monotonic staircase structure of integer QHE is similar to that of a 2D electron gas.

Figure 4
figure 4

(a) The Bz-dependent transverse conductivity at Ez = 0.29 eV/Å and EF = 0.06 eV. The same plots at Ez = 0.32 eV/Å for various EF’s are shown in (b–d). Also shown in the insets are the Bz-dependent LL energy spectra, with the Fermi levels represented by the dashed green lines.

Full size image

The dip and bulging structures appear frequently in σxy-Ez plots, as shown in Fig. 5(a,b) for different EF’s. The unusual staircase behavior begins when the Γ-group of LLs (in purple color) is formed at Ez > Ez,c, as seen in the insets. The higher value of EF is, the larger Ez,c is needed. Contrary to the results determined by varying Bz, the quantum number of the highest occupied LL in each group increases with Ez. Therefore, the plateau height is increased/reduced passing a LL from the outer/inner constant-energy loops, leading to the well-like staircases. The widths of these particular structures are strongly governed by the LL-spacings/Bz-strength.

Figure 5
figure 5

The Ez-dependent σxy at Bz = 30 T for different EF’s in (a,b). The corresponding Ez-dependent LL energy spectra are shown in the insets.

Full size image

The EF versus Bz phase diagram for the conductivity (color scale in units of 2e2/h) is helpful to give the whole picture of the feature-rich transport properties. With Ez > Ez,c (Fig. 6(a)), the Hall plateaus appear as colored bands diverging from the charge neutrality point at Bz → 0. For Bz < 10 T, the quantized number m around EF = 0 come in a regular order of odd ones, i.e., m = 1,3,5, etc., in correspondence to the D-group of LLs. With the increase of Bz, even m’s occur in an oscillatory fashion. The larger even value of m is, the weaker strength of Bz is required. The oscillation begins around the energy of saddle point (Ec ≈ 0.028 eV; Ev ≈ −0.035 eV), where the D-group LLs are turned into pairs of entangled LLs. The alternating appearance of odd and even m’s at low EF reveals the strong competitive and cooperative relations between the intralayer and interlayer atomic interactions and the Coulomb potentials.

Figure 6
figure 6

The EF−Bz−σxy phase diagram in (a) and that of Ez−BF−σxy in (b). The color scale represents the value of quantized number m, where m ≤ 15 in (a) and m ≤ 12 in (b). Also, the white arrow indicates the minimum value of Ez to induce the oscillation mode of even plateaus.

Full size image

The peculiar change of m is also seen in the Ez − EF − σxy phase diagram but with distinct features, as shown in Fig. 6(b). The zero plateau (m = 0) exists at Ez < 0.302, where the other higher plateaus obey the usual integer QHE, i.e., m = 1,2,3,4, etc. Increasing Ez diminishes the width of zero plateau and raises m for a chosen EF. In addition, beyond a critical value of Ez (indicated by the white arrow), the plateaus with an even m gradually turn into the oscillatory modes and finally disappear for further stronger Ez. At the same time, the half-integer QHE in units of 4e2/h is formed. The oscillatory behavior of σxy gets stronger away from EF = 0, corresponding to the more frequent LL anticrossings/crossings. The two phase plots suggest that one may increase Bz/Ez strength to lift/enhance the LL degeneracy, and to lead to the crossover from integer/half-integer to half-integer/integer QHEs. This provides an alternative to possible transport applications.

Conclusions

The strong electrically tunable energy bands are capable of enriching the quantization properties under a uniform perpendicular magnetic field \({B}_{z}\hat{z}\), such as producing two subgroups of Landau levels (LLs), uniform and non-uniform LL energy spacings, and frequent crossings and anti-crossings. Consequently, the magnetotransport properties of bilayer phosphore cover the integer and half-integer conductivities, the well-like, staircase and composite quantum structures, as well as different step heights and widths. The rich composite effects of intrinsic interactions and external fields are responsible for this. EF − Bz − σxy and Ez − EF − σxy phase plots reveal the transitions between insulator to conductor, integer to half-integer QHEs, and the oscillating quantized numbers.

Our predictions for the diverse quantum conductivities could be experimentally verified by magneto-transport measurements in a dual-gated system, as have been carried out/designed on few-layer graphene66,67,68, and phosphorene69,70. Phosphorene is anticipated to be an attractive candidate for designing unconventional thermoelectric devices39,40. These results could be further used to understand the magnetothermoelectric transport. In addition, the methodology is readily extended to other main-stream 2D systems, such as few-layer silicene, germanene, tinene, antomonene, bismuthene, etc. We sincerely believe that our systematic study could attract more experimental/theoretical researches on these emergent materials and accelerate their developments for device and energy applications.