Introduction

Intrinsic long-range ferromagnetism recently achieved in two-dimensional-limit van der Waals (vdW) crystals opens up great possibilities for both studying fundamental two-dimensional (2D) magnetism and engineering novel spintronic vdW heterostuctures1,2,3,4,5. Fe3GeTe2 is a promising candidate since its Curie temperature (Tc) in bulk is high and depends on the concentration of Fe atoms, ranging from 150 to 230 K6,7,8,9,10,11. Intrinsic magnetocrystalline anisotropy in few-layer counteracts thermal fluctuation and favors the 2D long-range ferromagnetism with a lower Tc of 130 K5. Most significantly, the Tc can be ionic-gate-tuned to room temperature in few-layers which is of high interest for electrically controlled magnetoelectronic devices12.

The layered Fe3−xGeTe2 displays a hexagonal structure belonging to the P63/mmc space group, where the 2D layers of Fe3−xGe sandwiched between nets of Te ions are weakly connected by vdW bonding [Fig. 1(a)]6. There are two inequivalent Wyckoff positions of Fe atoms which are denoted as Fe1 and Fe2. The Fe1-Fe1 dumbbells are situated in the centre of the hexagonal cell in the honeycomb lattice, composed of covalently bonded Fe2-Ge atoms. No Fe atoms occupy the interlayer space and Fe vacancies only occur in the Fe2 sites13. Local atomic environment is also studied by the Mössbauer and X-ray absorption spectroscopies14,15. Partially filled Fe d orbitals results in an itinerant ferromagnetism in Fe3−xGeTe216, which exhibits exotic physical phenomena such as nontrivial anomalous Hall effect17,18,19, Kondo lattice behavior20, strong electron correlations21, and unusual magnetic domain structures22,23. A second-step satellite transition T* is also observed just below Tc, and is not fully understood10,15.

Figure 1
figure 1

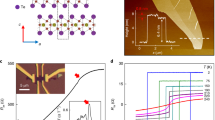
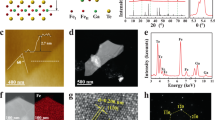
(a) Crystal structure and (b) X-ray energy-dispersive spectrum of Fe3−xGeTe2 single crystal. Inset shows a photograph of Fe3−xGeTe2 single crystal on a 1 mm grid. (c) X-ray diffraction (XRD) pattern of Fe3−xGeTe2. Inset shows the electron diffraction pattern taken along the [001] zone axis direction. (d) Temperature dependence of the reduced magnetization with out-of-plane field of Fe3−xGeTe2 fitted using spin-wave (SW) model and single-particle (SP) model. Inset shows the temperature dependence of zero-field-cooling (ZFC) magnetization of Fe3−xGeTe2 measured at H = 1 T applied along the c axis.

Full size image

Here we address the anisotropy in Fe3−xGeTe2 as well as the magnetocaloric effect investigated by heat capacity and dc magnetization measurements. The magnetocrystalline anisotropy is observed to be temperature-dependent. The magnetic entropy change ΔSM(T, H) also reveals an anisotropic characteristic and could be well scaled into a universal curve. Moreover, the \(-\Delta {S}_{M}^{{\max }}\) follows the power law of Hn with n = 0.603(6), and the relative cooling power RCP depends on Hm with m = 1.20(1).

Methods

High quality Fe3−xGeTe2 single crystals were synthesized by the self-flux technique14. The element analysis was performed using energy-dispersive X-ray spectroscopy (EDX) in a JEOL LSM-6500 scanning electron microscope (SEM). The selected area electron diffraction pattern was taken via a double aberration-corrected JEOL-ARM200F operated at 200 kV. The dc magnetization and heat capacity were measured in Quantum Design MPMS-XL5 and PPMS-9 systems with the field up to 5T.

Results and Discussion

The average stoichiometry of our flux-grown Fe3−xGeTe2 single crystals was determined by examination of multiple points. The actual concentration is determined to be Fe2.64(6)Ge0.87(4)Te2 [Fig. 1(b)], and it is referred to as Fe3−xGeTe2 throughout this paper. The as-grown single crystals are mirror-like and metallic platelets with the crystallographic c axis perpendicular to the platelet surface with dimensions up to 10 millimeters [inset in Fig. 1(b)]. In the 2θ X-ray diffraction pattern [Fig. 1(c)], only the (00l) peaks are detected, confirming the crystal surface is normal to the c axis. The corresponding electron diffraction pattern [inset in Fig. 1(c)] also confirms the high quality of single crystals.

Figure 1(d) presents the low temperature thermal demagnetization analysis for Fe3−xGeTe2 with out-of-plane field using both spin-wave (SW) model and single-particle (SP) model. The temperature dependence of zero-field-cooling (ZFC) magnetization M(T) for Fe3−xGeTe2 measured in H = 1 T applied along the c axis is shown in the inset of Fig. 1(d). Localized-moment spin-wave excitations can be described by a Bloch equation24,25,26:

$$\frac{\Delta M}{M(0)}=\frac{M(0)-M(T)}{M(0)}=A{T}^{3/2}+B{T}^{5/2}+\cdots ,$$
(1)

where A and B are the coefficients. The M(0) is the magnetization at 0 K, which is usually estimated from the extrapolation of M(T). The T 3/2 term stems from harmonic contribution and the T5/2 term is a high-order contribution in spin-wave dispersion relation. In an itinerant magnetism, it is a result of excitation of electrons from one subband to the other. The single-particle excitation is24:

$$\frac{\Delta M}{M(0)}=\frac{M(0)-M(T)}{M(0)}=C{T}^{3/2}exp\frac{-\Delta }{{k}_{B}T},$$
(2)

where C, Δ and kB are fit coefficient, the energy gap between the Fermi level and the top of the full subband and the Boltzmann constant, respectively. It can be seen that the SW model gives a better fit than the SP model up to 0.9 Tc [Fig. 1(d)], indicating possible localized moment, in agreement with the bad-metallic resistivity of Fe3−xGeTe215. It is also understandable that the SP model fails due to strong electron correlation in Fe3−xGeTe221. The fitting yields A = 8.4(7) × 10−5 K−3/2, B = 1.24(5) × 10−6 K−5/2, C = 3.4(1) × 10−4 K−3/2 and Δ = 3.9(4) meV.

Figure 2(a) shows the temperature dependence of heat capacity Cp for Fe3−xGeTe2 measured in zero-field and out-of-plane field of 2 and 5 T, respectively. The ferromagnetic order anomaly at Tc = 153 K in the absence of magnetic field is gradually suppressed in fields. The entropy S(T, H) can be determined by

$$S(T,H)={\int }_{0}^{T}\frac{{C}_{p}(T,H)}{T}dT.$$
(3)
Figure 2
figure 2

Temperature dependences of (a) the specific heat Cp, (b) the magnetic entropy change −ΔSM, and (c) the adiabatic temperature change ΔTad for Fe3−xGeTe2 with out-of-plane field changes of 2 and 5T.

Full size image

The magnetic entropy change ΔSM(T, H) can be approximated as ΔSM(T, H) = SM(T, H) − SM(T, 0). In addition, the adiabatic temperature change ΔTad caused by the field change can be derived by ΔTad(T, H) = T(S, H) − T(S, 0) at constant total entropy S(T, H). Figure 2(b,c) present the temperature dependence of −ΔSM and ΔTad estimated from heat capacity with out-of-plane field. They are asymmetric and attain a peak around Tc. The maxima of −ΔSM and ΔTad increase with increasing field and reach the values of 1.20 J kg−1 K−1 and 0.66 K, respectively, with the field change of 5 T. Since a large magnetic anisotropy is observed in Fe3−xGeTe2, it is of interest to further calculate its anisotropic magnetic entropy change.

Figure 3(a,b) present the magnetization isotherms with field up to 5 T applied in the ab plane and along the c axis, respectively, in temperature range from 100 to 200 K with a temperature step of 4 K. The magnetic entropy change can be obtained from dc magnetization measurement as27:

$$\Delta {S}_{M}(T,H)={\int }_{0}^{H}{[\frac{\partial S(T,H)}{\partial H}]}_{T}dH.$$
(4)
Figure 3
figure 3

Initial isothermal magnetization curves from T = 100 to 200 K with temperature step of T = 4 K measured with (a) in-plane and (b) out-of-plane fields. Temperature dependence of magnetic entropy change −ΔSM obtained with (c) in-plane and (d) out-of-plane field changes, and (e) the difference −\(\Delta {S}_{M}^{R}\).

Full size image

With the Maxwell’s relation \({[\frac{\partial S(T,H)}{\partial H}]}_{T}\) = \({[\frac{\partial M(T,H)}{\partial T}]}_{H}\), it can be rewritten as28:

$$\Delta {S}_{M}(T,H)={\int }_{0}^{H}{[\frac{\partial M(T,H)}{\partial T}]}_{H}dH.$$
(5)

When the magnetization is measured at small temperature and field steps, ΔSM(T, H) is approximated:

$$\Delta {S}_{M}(T,H)=\frac{{\int }_{0}^{H}M(T+\Delta T)dH-{\int }_{0}^{H}M(T)dH}{\Delta T}.$$
(6)

Figure 3(c,d) show the calculated −ΔSM(T, H) as a function of temperature in various fields up to 5 T applied in the ab plane and along the c axis, respectively. All the −ΔSM(T, H) curves feature a pronounced peak around Tc, similar to those obtained from heat capacity [Fig. 2(b)], and the peak broadens asymmetrically on both sides with increase in field. Moreover, the value of −ΔSM(T, H) increases monotonically with increase in field; the peak −ΔSM reaches 1.26 J kg−1 K−1 with in-plane field change and 1.44 J kg−1 K−1 with out-of-plane change of 5 T, respectively. We calculated the rotating magnetic entropy change \(\Delta {S}_{M}^{R}\) as

$$\Delta {S}_{M}^{R}(T,H)=\Delta {S}_{M}(T,{H}_{c})-\Delta {S}_{M}(T,{H}_{ab}).$$
(7)

The asymmetry of −ΔSM(T, H) is more apparent in the temperature dependence of −\(\Delta {S}_{M}^{R}\) [Fig. 3(e)]. Furthermore, there is a slight shift of −ΔSM maximum towards higher temperature when the field varies from 1 to 5 T [Fig. 3(c,d)]. This shift of Tpeak excludes the mean field model but could be reproduced by the Heisenberg model due to its discrepancy with Tc29.

Around the second order phase transition30, the magnetic entropy maximum change is \(-\Delta {S}_{M}^{{\max }}\) = aHn 31, where a is a constant and n is32

$$n(T,H)=dln|\Delta {S}_{M}|/dln(H).$$
(8)

Figure 4(a) shows the temperature dependence of n(T) in various fields. All the n(T) curves follow an universal behavior33. At low temperatures, n has a value close to 1. At high temperatures, n tends to 2 as a consequence of the Curie-Weiss law. At T = Tc, n has a minimum. Additionally, the exponent n at Tc is related to the critical exponents30:

$$n({T}_{c})=1+(\frac{\beta -1}{\beta +\gamma })=1+\frac{1}{\delta }(1-\frac{1}{\beta }),$$
(9)
Figure 4
figure 4

(a) Temperature dependence of n in various fields. (b) Field dependence of the maximum magnetic entropy change \(-\Delta {S}_{M}^{{\max }}\) and the relative cooling power RCP with power law fitting in red solid lines. (c) The normalized ΔSM as a function of the rescaled temperature t with out-of-plane field and in-plane field (inset). (d) Scaling plot based on the critical exponents β = 0.372 and γ = 1.26514.

Full size image

where β, γ, and δ are the critical exponents related to the spontaneous magnetization Ms below Tc, the inverse initial susceptibility H/M above Tc, and the isotherm M(H) at Tc, respectively.

Relative cooling power (RCP) could be used to estimate the cooling efficiency34:

$$RCP=-\,\Delta {S}_{M}^{max}\times \delta {T}_{FWHM},$$
(10)

where \(-\Delta {S}_{M}^{{\max }}\) is the entropy change maximum around Tc and δTFWHM is the width at half maximum. The RCP also depends on the field as RCP = bHm, where b is a constant and m is related to the critical exponent δ:

$$m=1+\frac{1}{\delta }.$$
(11)

Figure 4(b) presents the field-dependent \(-\Delta {S}_{M}^{{\max }}\) and RCP. The RCP is 113.3 J kg−1 within field change of 5 T for Fe3−xGeTe2. This is one half of those in manganites and much lower than in ferrites35,36. Fitting of the \(-\Delta {S}_{M}^{{\max }}\) and RCP gives n = 0.603(6) and m = 1.20(1), which are close to the values estimated from the critical exponents (Table 1).

Table 1 Critical exponents of Fe3−xGeTe214. The MAP, KFP and CI represent the modified Arrott plot, the Kouvel-Fisher plot and the critical isotherm, respectively.
Full size table

The scaling of magnetocaloric data is constructed by normalizing all the −ΔSM curves against the maximum \(-\Delta {S}_{M}^{{\max }}\), namely, ΔSM/\(\Delta {S}_{M}^{{\max }}\) by rescaling the temperature t below and above Tc as defined in:

$${t}_{-}=({T}_{peak}-T)/({T}_{r1}-{T}_{peak}),T < {T}_{peak},$$
(12)
$${t}_{+}=(T-{T}_{peak})/({T}_{r2}-{T}_{peak}),T > {T}_{peak},$$
(13)

where Tr1 and Tr2 are the temperatures of two reference points corresponding to \(\Delta {S}_{M}({T}_{r1},{T}_{r2})=\frac{1}{2}\Delta {S}_{M}^{max}\)37. All the −ΔSM(T, H) curves collapse onto a single curve regardless of temperature and field, as shown in Fig. 4(c). In the phase transition region, the scaling analysis of −ΔSM can also be expressed as

$$\frac{-\Delta {S}_{M}}{{a}_{M}}={H}^{n}f(\frac{\varepsilon }{{H}^{1/\Delta }}),$$
(14)

where aM = Tc−1Aδ+1B with A and B representing the critical amplitudes as in Ms(T) = A(−ε)β and H = BMδ, Δ = β + γ, and f(x) is the scaling function38. If the critical exponents are appropriately chosen, the −ΔSM(T) curves should be rescaled into a single curve, consistent with normalizing all the −ΔSM curves with two reference temperatures. By using the values of β = 0.372 and γ = 1.265 obtained by the Kouvel-Fisher plot14, we have replotted the scaled −ΔSM for Fe3−xGeTe2 [Fig. 4(d)]. The good overlap of the experimental data points clearly indicates that the obtained critical exponents for Fe3−xGeTe2 are not only in agreement with the scaling hypothesis but also intrinsic.

Then we estimated the magnetocrystalline anisotropy of Fe3−xGeTe2. By using the Stoner-Wolfarth model a value for the magnetocrystalline anisotropy constant Ku can be estimated from the saturation regime in isothermal magnetization curves [Fig. 5(a)]39. Within this model the magnetocrystalline anisotropy in the single domain state is related to the saturation magnetic field Hs and the saturation moment Ms with μ0 is the vacuum permeability:

$$\frac{2{K}_{u}}{{M}_{s}}={\mu }_{0}{H}_{sat}.$$
(15)
Figure 5
figure 5

(a) Initial isothermal magnetization curves from T = 10 to 140 K with in-plane fields. Temperature evolution of (b) the saturation magnetization Ms, (c) the saturation field Hs, and (d) the anisotropy constant Ku.

Full size image

When H//ab, the anisotropy becomes maximal. We estimated the saturation magnetization Ms by using a linear fit of M(H) above a magnetic field of 2.5 T with in-plane field [Fig. 5(b)], which monotonically decreases with increasing temperature. Then we determined the saturation field Hs as the intersection point of two-linear fits, one being a fit to the saturated regime at high fields and one being a fit of the unsaturated linear regime at low fields. The value of Hs increases at low temperature, which is possibly related to a spin reorientation transition15, and then decreases with increasing temperature [Fig. 5(c)]. Figure 5(d) presents the temperature evolution of Ku for Fe3−xGeTe2, which can not be described by the l(l + 1)/2 power law40,41. The value of Ku for Fe3−xGeTe2 is about 69 kJ cm−3 at 10 K, slightly increases to 78 kJ cm−3 at 50 K, and then decrease with increasing temperature, which are comparable to those for CrBr3, but smaller than those for CrI342. The decrease of Ku with increasing temperature is also observed in CrBr3 and CrI342, arising from a large number of local spin clusters43,44. In a pure two-dimensional system, materials with isotropic short-range exchange interactions can not magnetically order. The long-range ferromagnetism in few-layers of Fe3−xGeTe2 could possibly be favored by the large magnetocrystalline anisotropy.

Conclusion

In summary, we have investigated in detail the magnetocaloric effect of Fe3−xGeTe2 single crystals. The large magnetocrystalline anisotropy is found to be temperature-dependent and probably establishes the long-range ferromagnetism in few-layers of Fe3−xGeTe2. The magnetic entropy change −ΔSM also reveals an anisotropic characteristic and could be well scaled into a universal curve independent on temperature and field. By fitting of the field-dependent parameters of \(-\Delta {S}_{M}^{{\max }}\) and the relative cooling power RCP, it gives \(-\Delta {S}_{M}^{{\max }}\)∝Hn with n = 0.603(6) and RCP ∝ Hm with m = 1.20(1) when H//c. Considering its tunable room-temperature ferromagnetism and hard magnetic properties in nanoflakes, further investigation on the size dependence of magnetocaloric effect is of interest.