Rabi splitting and optical Kerr nonlinearity of quantum dot mediated by Majorana fermions

Abstract

Majorana fermions (MFs), due to their significance in fundamental physics and potential applications in topological quantum computation based on solid-state devices, have drawn widespread attention. Here, we design a hybrid semiconductor/superconductor ring (S/SR) device and put forward an optical method for detecting a pair of MFs in the S/SR device with a quantum dot (QD) with the popular optical pump-probe scheme, which is very different from the present electrical method only considering one nearby MF coupled to the QD. The symmetric and unsymmetric Rabi splitting and optical Kerr nonlinear effect of QD mediated by MFs are investigated under uncoupled and coupled majorana modes, respectively. The coherent optical spectra indicate that a pair of MFs coupled to the QD induced remarkable splitting under different parameters regime and the physical origin of these phenomena are elaborated detailedly. Due to QD-MFs coupling, the probe absorption spectra present the phenomenon of Majorana modes induced transparency (MMIT) which will induce remarkable phenomena of slow light. The coherent optical spectra afford a potential supplement for probing MFs and support Majorana fermions-based topological quantum computation.

Introduction

Majorana fermions (MFs) are exotic particles whose antiparticle is itself $\gamma ={\gamma }^{\dagger }$ obeying non-Abelian statistics. Therefore MFs can realize subsequent potential applications in topological quantum computation and quantum information processing¹. Despite proposed initially to investigate neutrinos, one has discovered the analogous Majorana zero modes in condensed matter systems². Currently, Majorana signature have been observed experimentally in various hybrid systems including hybrid semiconducting nanowire (atomic chains)/superconductor structure^3,4,5,6,7, iron-based superconductor⁸, topological structure^9,10, and quantum anomalous Hall insulator–superconductor structure¹¹. For detecting MFs, several typical means have also been presented experimentally, such as zero-bias peaks (ZBPs) in tunneling spectroscopy^3,4,5,6,7, fractional a.c. Josephson effect¹², Coulomb blockade spectroscopy experiment⁹, and spin-polarized scanning tunneling microscopy¹³. We notice that most of the recent theories and experiments for researching and detecting MFs proposed and carried out focus on electrical scheme, and other effective and alternative methods, for example, all-optical means for probing Majorana bound states have received less attention.

On the other hand, nanostructures such as quantum dots (QDs) have been obtained remarkable progress in modern nano-science and nano-technology in recent years¹⁴. QD, consiered as a simple stationary “artificial atom” with well optical property¹⁵, lays the foundation for numerous potential applications¹⁶, where the significant applications including entanglement concentration, logic gate construction and entangled state preparation with optical Kerr nonlinear effect have drawn widespread attention^14,17,18. The optical Kerr nonlinear effect manifested by the third-order optical Kerr nonlinearity of QD, which is essential for light-controlled phase and refractive index modulation in various fields such as optical telecommunications, optical data storage, and information processing^14,19. If coupling the QD to metallic nanoparticle (MNP)^20,21, the plasmon resonance on MNP will amplify the local field near the QD and thereby intensify the mechanically induced optical Kerr nonlinearity, which will realize several orders of magnitude in the optical Kerr effect larger than in intrinsic Si and other hybrid systems²². Further, the detection of MFs with the QD have been proposed theoretically^{23,24,25,26,27}, and most recently Majorana bound states have been investigated at the end of epitaxial hybrid Sm-S nanowires using tunneling spectroscopy through QDs²⁸. However, in these schemes, QD is consider as only one resonant level with single spin state^{23,24,25,26,27}, and we will consider the QD as a two-level system (TLS) (as shown in Fig. 1(b)) which is different from previous theoretical schemes for detecting MFs.

Figure 1

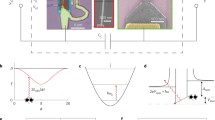
(a) shows a semiconducting ring with strong spin-orbit interaction in an external aligned parallel magnetic field B is placed on the surface of a superconducting ring different from the previous work^3,6, and a couple of Majorana fermions (MFs) emerge at the end of semiconducting ring. A quantum dot (QD) driven by the pump-probe technology is introduced to probe a pair of MFs signature. When a couple of MFs appear in the semiconducting ring and interact with the QD, Majorana signatures will be brought out with the coherent optical spectra of the QD. (b) The energy-level of the QD interact with two MFs. (c) We consider the QD as a TLS rather than only owns one resonant level with single spin state in the electrical detection means^{23,24,25,26,27}, and the QD coupled to a couple of MFs will induce the coupled states $|\mathrm{0,}\,{n}_{MF}\rangle$, $|\mathrm{0,}\,{n}_{MF}+1\rangle$, $|\mathrm{1,}\,{n}_{MF}\rangle$ and $|\mathrm{1,}\,{n}_{MF}+1\rangle$ (n_MF denotes MFs number states).

In this work, rather than previous schemes for probing MFs in electrical domain, firstly, we design a hybrid semiconductor/superconductor ring (S/SR) device as shown in Fig. 1(a), and the QD is driven by the optical pump-probe technology²⁹ for detecting a couple of MFs emerging in the ends of the semiconducting nanowire ring under in a magnetic field. Due to the QD has no direct contact with the S/SR device, the scheme is immune to the disturbance of other signals in detecting of MFs with the optical means. Once a couple of MFs appear at the end of the nanowire ring and have interaction with the QD, the signatures of MFs will be brought out with the coherent optical response. Secondly, we further investigate the Rabi splitting and optical Kerr nonlinear effect of QD mediated by MFs. The probe absorption spectra present symmetrical and asymmetrical Rabi splitting under uncoupled MFs modes (ϵ_MF = 0) and coupled MFs modes (ϵ_MF ≠ 0), respectively. When a pair of MFs couple to the QD, the Rabi splitting is enhanced, which depends on the coupling strength between a pair of MFs and the QD. With adjusting the exciton resonant detuning and Majorana resonant detuning, the probe absorption intensity and the peak width of splitting are enhanced significantly. The optical Kerr nonlinear phenomena are also investigated under different parameter regions, and the peak width of splitting in the optical Kerr spectrum depends on the coupling strength and resonant detuning.

Results

The Model and Hamiltonian

Figure 1 shows a QD coupled to a pair of MFs emerging in the hybrid S/SR device. We consider the QD as a TLS which include the ground state $|g\rangle$ and the single exciton state $|e\rangle$^30,31, and its Hamiltonian can be described as H_QD = ℏω_eS^z, where ω_e is the exciton frequency. We introduce the pseudo-spin operators S^z and S^± to describe the QD, which has the commutation relations [S^z, S^±] = ±S^± and [S⁺, S⁻] = 2S^z. In order to describe MFs, we also introduce an operator γ_M with relation ${\gamma }_{M}^{\dagger }={\gamma }_{M}$ $({\gamma }_{M}^{2}=1)$ due to MFs are their own antiparticle. Then the coupling Hamiltonian of QD and a pair of MFs γ_M1 and γ_M2 is^{23,24,25,26,27}.

$${H}_{int}=i{\epsilon }_{MF}{\gamma }_{M1}{\gamma }_{M2}/2+i\hslash {\beta }_{1}({S}^{-}-{S}^{+}){\gamma }_{M1}+i\hslash {\beta }_{2}({S}^{-}-{S}^{+}){\gamma }_{M2},$$

(1)

the above Hamiltonian includes three parts, the first one is iϵ_MFγ_M1γ_M2/2 which gives the energy of MFs (${\epsilon }_{MF}=\hslash {\omega }_{MF} \sim {e}^{-l/\xi }$, ω_MF is the Majorana frequency, l is the semiconductor length, and ξ is the superconductor coherent length). If l is long enough, ϵ_MF will be close to zero. We will investigate the two conditions detailedly in the following section and define them as the coupled- (ϵ_MF ≠ 0) and uncoupled-Majorana modes (ϵ_MF = 0). The second and the third term describe a pair MFs coupled to the QD with the coupling strengths β₁ and β₂, and the coupling strengths relate to the distance between the QD and S/SR device. For simplicity, the Majorana representation γ_M is transformed to the usual fermion operator with the transformation of ${\gamma }_{M1}={f}_{M}^{\dagger }+{f}_{M}$ and ${\gamma }_{M2}=i({f}_{M}^{\dagger }-{f}_{M})$, where ${f}_{M}^{\dagger }$ (f_M) is the fermion creation (annihilation) operator. Using rotating wave approximation³², Eq. (1) can be rewritten as

$${H}_{MFs-QD}={\epsilon }_{MF}({f}_{M}^{\dagger }{f}_{M}-1/\mathrm{2)}+i\hslash {\beta }_{1}({S}^{-}{f}_{M}^{\dagger }-{S}^{+}{f}_{M})-\hslash {\beta }_{2}({S}^{-}{f}_{M}^{\dagger }+{S}^{+}{f}_{M}\mathrm{).}$$

(2)

We have neglected the non-conservation term of energy incluing $i\hslash {\beta }_{1}({S}^{-}{f}_{M}-{S}^{+}{f}_{M}^{+})$ and $\hslash {\beta }_{2}({S}^{-}{f}_{M}+{S}^{+}{f}_{M}^{+})$, and numerical results indicate that the influence of them are too weak to be considered in the theoretical treatment.

The Hamiltonian of ${H}_{QD-F}=-\,\mu {E}_{c}({S}^{+}{e}^{-i{\omega }_{c}t}+{S}^{-}{e}^{i{\omega }_{c}t})-\mu {E}_{s}({S}^{+}{e}^{-i{\omega }_{s}t}+{S}^{-}{e}^{i{\omega }_{s}t})$ indicates a strong pump laser and a weak probe laser simultaneously irradiating to the QD³³ and has a interaction with the QD, in which μ is the electric dipole moment of the QD, ω_c and ω_s with light intensity E_c and E_s are the frequencies of the pump laser and probe laser fields, respectively. We use the rotating frame of the pump laser frequency ω_c, and then obtain the full Hamiltonian of our hybrid system³⁴

$$\begin{array}{c}H=\hslash {{\rm{\Delta }}}_{c}{S}^{z}+\hslash {{\rm{\Delta }}}_{MF}({f}_{M}^{\dagger }{f}_{M}-1/\mathrm{2)}+i\hslash {\beta }_{1}({S}^{-}{f}_{M}^{\dagger }-{S}^{+}{f}_{M})-\hslash {\beta }_{2}({S}^{-}{f}_{M}^{\dagger }+{S}^{+}{f}_{M})\\ \,-\hslash {{\rm{\Omega }}}_{c}({S}^{+}+{S}^{-})-\mu {E}_{s}({S}^{+}{e}^{-i\delta t}+{S}^{-}{e}^{i\delta t}),\end{array}$$

(3)

where Δ_c = ω_e − ω_c is the exciton-pump field detuning, Δ_MF = ω_MF − ω_c is the Majorana-pump field detuning, and δ = ω_s − ω_c is the probe-pump detuning. Ω_c = μE_c/ℏ indicates the Rabi frequency of the pump field.

The Quantum Langevin Equations (QLEs)

We use the Heisenberg equation of motion iℏ∂_tρ = [ρ, H] (ρ = S^z, S⁻, f_M) and introduce corresponding damping and noise operators, we obtain the QLEs as³⁵:

$${\partial }_{t}{S}^{z}=-\,{{\rm{\Gamma }}}_{1}({S}^{z}+1/\mathrm{2)}-{\beta }_{1}({S}^{-}{f}_{M}^{\dagger }+{S}^{+}{f}_{M})-i{\beta }_{2}({S}^{-}{f}_{M}^{\dagger }+{S}^{+}{f}_{M})+i{{\rm{\Omega }}}_{c}({S}^{+}-{S}^{-})\,+(i\mu {E}_{s}/\hslash )({S}^{+}{e}^{-i\delta t}-h\mathrm{.}c),$$

(4)

$${\partial }_{t}{S}^{-}=-(i{{\rm{\Delta }}}_{c}+{{\rm{\Gamma }}}_{2}){S}^{-}+\mathrm{2(}{\beta }_{1}-i{\beta }_{2}){S}^{z}{f}_{M}-2i{{\rm{\Omega }}}_{c}{S}^{z}-2i\mu {E}_{s}{e}^{-i\delta t}{S}^{z}/\hslash +{\tau }_{in}(t),$$

(5)

$${\partial }_{t}{f}_{M}=-(i{{\rm{\Delta }}}_{MF}+{\kappa }_{M}/\mathrm{2)}{f}_{M}+({\beta }_{1}+i{\beta }_{2}){S}^{-}+\hat{\xi }(t),$$

(6)

where Γ₁ (Γ₂) is the relaxation rate (dephasing rate) of the exciton, and κ_M is MFs decay rate. τ_in(t) describe the Langevin noise follows the relations of $\langle {\tau }_{in}(t){\tau }_{in}^{\dagger }(t^{\prime} )\rangle \sim \delta (t-t^{\prime} )$ and 〈τ_in(t)〉 = 0. MFs are also influenced by stochastic force process with the following correlation function

$$\langle {\hat{\xi }}^{+}(t)\hat{\xi }(t^{\prime} )\rangle =\frac{{\kappa }_{M}}{{\omega }_{MF}}\int \frac{d\omega }{2\pi }\omega {e}^{-i\omega (t-t^{\prime} )}[1+\,\coth (\frac{\hslash \omega }{2{\kappa }_{B}T})],$$

(7)

where k_B is Boltzmann constant, T indicates the reservoir temperature. In Eq. (7), both the Brownian processes and non-Markovian processes³⁶ will influence Majorana modes, and the quantum signatures of MFs modes can be observed only in the case of resolved sideband regime, i.e., ω_MF/κ_M >> 1 under low temperature T. In the weak coupling regime, the effect of Brownian noise is modeled as Markovian processes. Further, the interaction between the QD and MFs is stronger than the interation with the reservoir, considering second order approximation³⁶, then the reservoir that affects Majorana modes can be obtained as shown in Eq. (7).

The Coherent Optical Response of QD

When the QD is driven by a strong pump laser, the Heisenberg operator can be divided into two parts, i.e., steady-state mean value ρ₀, and small fluctuation δρ with zero mean value 〈δρ〉 = 0. To solve the steady-state values, we obtain the the steady-state population inversion (${\theta }_{0}=2{S}_{0}^{z}$) as follows

$$\begin{array}{c}{{\rm{\Gamma }}}_{1}({\theta }_{0}+\mathrm{1)[}{\theta }_{0}^{2}{({\beta }_{1}^{2}+{\beta }_{2}^{2})}^{2}-{\theta }_{0}({\beta }_{1}^{2}+{\beta }_{2}^{2})({{\rm{\Gamma }}}_{2}{\kappa }_{M}-2{{\rm{\Delta }}}_{c}{{\rm{\Delta }}}_{MF})\\ +({{\rm{\Delta }}}_{c}^{2}+{{\rm{\Gamma }}}_{2}^{2})({{\rm{\Delta }}}_{MF}^{2}+{\kappa }_{M}^{2}/\mathrm{4)]}+4{{\rm{\Omega }}}_{c}^{2}{\theta }_{0}{{\rm{\Gamma }}}_{2}({{\rm{\Delta }}}_{MF}^{2}+{\kappa }_{M}^{2}/\mathrm{4)}=0.\end{array}$$

(8)

We here make the ansatz to solve the fluctuation equation³³ 〈δρ〉 = ρ₊e^−iδt + ρ₋e^iδt, solving the fluctuation equation set, the linear optical susceptibility is ${\chi }_{eff}^{\mathrm{(1)}}({\omega }_{s})=\mu {S}_{+}({\omega }_{s})/{E}_{s}=({\mu }^{2}/\hslash {{\rm{\Gamma }}}_{2}){\chi }^{\mathrm{(1)}}({\omega }_{s})$, and χ⁽¹⁾(ω_s) is given by

$${\chi }^{\mathrm{(1)}}({\omega }_{s})=\frac{[{\varepsilon }_{7}{{\rm{\Pi }}}_{1}({{\rm{\Lambda }}}_{4}+{\varepsilon }_{3}{{\rm{\Pi }}}_{2})-i{\theta }_{0}{{\rm{\Lambda }}}_{4}]{{\rm{\Gamma }}}_{2}}{{{\rm{\Lambda }}}_{1}{{\rm{\Lambda }}}_{4}+{{\rm{\Pi }}}_{1}{{\rm{\Pi }}}_{2}{\epsilon }_{3}{\epsilon }_{4}},$$

(9)

where Π₁ = 2[(β₁ − iβ₂)f_M0 − iΩ_c], Π₂ = 2[(β₁ + iβ₂)f_M0 + iΩ_c], ϵ₁ = (β₁ + iβ₂)/[i(Δ_MF − δ) + κ_M/2], ϵ₂ = (β₁ + iβ₂)/[i(Δ_MF + δ) + κ_M/2], ${\epsilon }_{3}=[i{{\rm{\Omega }}}_{c}-({\beta }_{1}-i{\beta }_{2}){f}_{M0}-({\beta }_{1}+i{\beta }_{2}){S}_{0}{\epsilon }_{2}^{\ast }]/({{\rm{\Gamma }}}_{1}-i\delta )$, ${\epsilon }_{4}=[i{{\rm{\Omega }}}_{c}+({\beta }_{1}+i{\beta }_{2}){f}_{M0}^{\ast }$$+({\beta }_{1}-i{\beta }_{2}){S}_{0}^{\ast }{\epsilon }_{1}]/({{\rm{\Gamma }}}_{1}-i\delta )$, ${\epsilon }_{5}=[i{{\rm{\Omega }}}_{c}-({\beta }_{1}-i{\beta }_{2}){f}_{M0}-({\beta }_{1}+i{\beta }_{2}){S}_{0}{\epsilon }_{1}^{\ast }]/({{\rm{\Gamma }}}_{1}+i\delta )$, ${\epsilon }_{6}=[i{{\rm{\Omega }}}_{c}+({\beta }_{1}+i{\beta }_{2}){f}_{M0}^{\ast }+({\beta }_{1}-i{\beta }_{2}){S}_{0}^{\ast }{\epsilon }_{2}]/({{\rm{\Gamma }}}_{1}+i\delta )$, ${\epsilon }_{7}=i{S}_{0}^{\ast }/({{\rm{\Gamma }}}_{1}-i\delta )$, ϵ₈ = iS₀/(Γ₁ + iδ), Λ₁ = i(Δ_c − δ) + Γ₂ − θ₀(β₁ − iβ₂)ϵ₁ + Π₁ϵ₄, ${{\rm{\Lambda }}}_{2}=-i({{\rm{\Delta }}}_{c}-\delta )+{{\rm{\Gamma }}}_{2}-{\theta }_{0}({\beta }_{1}+i{\beta }_{2}){\epsilon }_{1}^{\ast }-{{\rm{\Pi }}}_{2}{\epsilon }_{5}$, Λ₃ = i(Δ_c + δ) + Γ₂ − θ₀(β₁ − iβ₂)ϵ₂ + Π₁ϵ₆, Λ₄ = −i(Δ_c + δ) + Γ₂ − θ₀(β₁ + iβ₂)ϵ₁ + Π₂ϵ₃. The real and imaginary parts of χ⁽¹⁾(ω_s) show the dispersion and absorption, respectively. The nonlinear optical susceptibility can be calculated as ${\chi }_{eff}^{\mathrm{(3)}}({\omega }_{s})=\mu {S}_{-}({\omega }_{s})/\mathrm{(3}{E}_{c}^{2}{E}_{s})={\Sigma }_{3}{\chi }^{\mathrm{(3)}}({\omega }_{s})$, where ${\Sigma }_{3}={\mu }^{4}/\mathrm{(3}{\hslash }^{3}{{\rm{\Gamma }}}_{2}^{3})$, and χ⁽³⁾(ω_s) is given by

$${\chi }^{\mathrm{(3)}}({\omega }_{s})=-\,\frac{{{\rm{\Pi }}}_{1}[{\epsilon }_{8}({{\rm{\Lambda }}}_{2}+{\epsilon }_{5}{{\rm{\Pi }}}_{2})-i{\theta }_{0}{\epsilon }_{5}]{{\rm{\Gamma }}}_{2}^{3}}{[{{\rm{\Lambda }}}_{2}{{\rm{\Lambda }}}_{3}+{{\rm{\Pi }}}_{1}{{\rm{\Pi }}}_{2}{\epsilon }_{5}{\epsilon }_{6}]{{\rm{\Omega }}}_{c}^{2}}.$$

(10)

The real and imaginary parts of χ⁽³⁾(ω_s) characterize the Kerr coefficient and nonlinear absorption, respectively.

The Numerical Results

We use the realistic parameters for the QD³⁷: Γ₁ = 0.3 GHz and Γ₂ = Γ₁/2. According to several recent experiment reports^3,4,5,6,7, we expect that the decay rate κ_M = 0.1 × 10⁶ Hz. For the coupling strength β of the QD and MFs, we use the previous published work³⁸, and the numerical value is β = 0.05 × 10⁹ Hz which is related to the distance between the QD and the hybrid S/SR device as shown in Fig. 1.

Firstly, we consider uncoupled majorana modes (i.e. ϵ_MF = 0), that is to say the two MFs are not coupled to each other and probe field is resonant with the exciton frequency (i.e. Δ_c = 0). In this situation, the Hamiltonian of the coupled QD-MFs can be reduced to ${H}_{QD-MFs}=i\hslash {\beta }_{1}({S}^{-}{f}_{M}^{\dagger }-{S}^{+}{f}_{M})-\hslash {\beta }_{2}({S}^{-}{f}_{M}^{\dagger }+{S}^{+}{f}_{M})$, which is similar to the J-C Hamiltonian in quantum optics. Figure 2(a) displays the probe absorption spectra of the probe laser (i.e., the imaginary part of the dimensionless susceptibility Im χ⁽¹⁾) vs. the detuning Δ_s (Δ_s = ω_s − ω_e) under several different QD-MFs coupling strengths. The black solid curve in Fig. 2(a) shows the result of no QD-MFs coupling, which present Lorentz line shape under weak pump laser driven. When a pair of MFs emerge in the end of the hybrid S/SR device and interact with the two-level QD, the absorption spectrum presents a symmetric Rabi splitting when β₁ = 0.05 × 10⁹ Hz and β₂ = 0 as shown the red curve in Fig. 2(a). Thus, the symmetric Rabi splitting in the probe absorption reveals a true signature of MFs emerge in the hybrid S/SR device. To determine the symmetric Rabi splitting of the QD is induced by MFs modes rather than other regimes induced the Majorana-like signatures, we consider several conditions. Due to Kondo effect can also leads to analogous Majorana signatures, it is necessary to distinguish the true Majorana signatures and Kondo effect. Kondo effect, in the detection of MFs with electrical methods, is generally related to the strong coupling to two normal leads in he hybrid S/SR structure, and when the Kondo temperature T_k is smaller than the gap, a superconducting gap can suppress the effect. Recently, to control Kondo effect, Nadj-Perge et al. have reported an experimental project of the hybrid Fe-atoms-chain/Pb-superconductor (Fe/Pb) substrate⁶, and the present another evidence in the scheme is related to superconductivity and rather than with other phenomena. Therefore, in a way, the Fe/Pb substrate can replace the hybrid S/SR structure. On the other hand, due to there are several normal electrons in semiconductor nanowire ring, so it is necessary to determine whether the signals in the probe absorption spectra are true QD-MFs coupling, rather than the interation between the QD and the electrons in the nanowire induced the same Majorana signals. For this question, we once have used the tight-binding Hamiltonian³⁴ to elucidate the electrons in nanowire, and the numerical results indicate MFs signatures in the coherent optical spectra are the true MFs signals³⁴.

Figure 2

(a) and (b) The probe absorption spectra of probe field vs. the probe detuning Δ_s under ϵ_MF = 0 and Δ_c = 0 with several different QD-MFs coupling strengths. The parameters used are Γ₁ = 0.3 GHz, Γ₂ = 0.15 GHz, κ_M = 0.1 MHz, ${{\rm{\Omega }}}_{c}^{2}=0.005$(GHz)².

When a pair of MFs couple to the QD (β₁ = 0.05 GHz, β₂ = 0.05 GHz), the peak width of Rabi splitting induced by MFs is enhanced significantly (the blue curve in Fig. 2(a)), and the bigger QD-MFs coupling induced larger peak width of splitting as green curve in Fig. 2(a). In Fig. 2(b), we also show three different QD-MFs coupling strength, i.e. (β₁ = 0.05 GHz, β₂ = 0.05 GHz), (β₁ = 0.07 GHz, β₂ = 0.03 GHz), and (β₁ = 0.09 GHz, β₂ = 0.01 GHz). The results indicate that the peak width of Rabi splitting depends on one of the pair of MFs coupling to the QD. The physical origin of such results are due to the coherent interaction between the QD and MFs, and we introduce the dressed-state theory to describe the interation between the QD and MFs for interpreting this physical phenomena. Due to the QD is considered as a TLS with the ground state $|0\rangle$ and exciton state $|1\rangle$, when QD couple to MFs, the two-level QD will be embellish by MFs number states n_MF and generate four Majorana dressed states, i.e., $|\mathrm{0,}\,{n}_{MF}\rangle$, $|\mathrm{0,}\,{n}_{MF}+1\rangle$, $|\mathrm{1,}\,{n}_{MF}\rangle$, $|\mathrm{1,}\,{n}_{MF}+1\rangle$, where n_MF indicates MFs number states as shown in Fig. 1(c). Then, in Fig. 2, the left sharp peaks of Rabi splitting shows the transition from $|0\rangle$ to $|\mathrm{1,}\,{n}_{MF}\rangle$, and the right one gives the transition between $|0\rangle$ and $|\mathrm{1,}\,{n}_{MF}+1\rangle$.

Secondly, we consider coupled Majorana modes (ϵ_MF ≠ 0) and Δ_c = 0 as shown in Fig. 3. In this condition, the interaction between the two MFs should be taken into consideration. As in uncoupled Majorana modes, if there is no QD-MFs coupling, the spectrum (the black curve in Fig. 3(a)) shows the same Lorentz line shape. When a pair of MFs coupled to the QD, the spectra display unsymmetric Rabi splitting under the detuning Δ_MF = −0.5 × 10⁹ Hz. Figure 3(b) is the detail parts of the left peaks in Fig. 3(a), and sharp peak locates at Δ_s = −0.5 GHz which is different from in uncoupled majorana modes. In Fig. 3(c), we further discuss several different QD-MFs coupling strength, the results in probe absorption spectra manifest that when the QD is close to one MF (such as γ_M1, and then β₁ > β₂), the width of unsymmetric Rabi splitting is larger than the case of β₁ = β₂, and Fig. 3(d) is the detail parts of the left peaks in Fig. 3(c). The QD-MFs coupling strength can be controlled with controlling the distance of the QD and the hybrid S/SR device. The results in Fig. 2 and Fig. 3 manifest that the signals are the ture MFs signature, and our all-optical detection means can work at the coupled- and uncoupled-Majorana edge states³⁸.

Figure 3

(a) The probe absorption spectra at coupled majorana modes (ϵ_MF ≠ 0) and Δ_c = 0. (b) The detail parts of the left peaks in (a). (c) The probe absorption spectra in the condition of a pair MFs coupled the QD. (d) The detail parts of the left peaks in (c).

In addition, when making a comparison between ϵ_MF ≠ 0 in Fig. 3 and ϵ_MF = 0 in Fig. 2, we find that the probe absorption spectra show the analogous phenomenon of electromagnetically induced transparency (EIT)³⁹ in the two situations. The absorption dip approaches zero at Δ_s = 0 and Δ_s = −0.5 × 10⁹ Hz under ϵ_MF = 0 and ϵ_MF ≠ 0, respectively, which indicates the probe field is transmitted with experiencing nothing absorption. The result is due to the destructive quantum interference effect between the beat frequency δ (δ = ω_s − ω_c) of the two optical fields (i.e. pump laser field and probe laser field) via the QD and Majorana modes³⁸. When the beat frequency δ approximates to the MFs resonance frequency ω_MF, then Majorana modes start oscillating coherently resulting in Stokes-like (Δ_SM = ω_c − ω_MF) and anti-Stokes-like (Δ_ASM = ω_c + ω_MF) light scattering from the QD. In highly off-resonant, the process of Δ_SM is strongly suppressed, and only leaving the process of Δ_ASM interferes with the probe field modifying the absorption spectra. We therefore define the phenomenon as Majorana modes induced transparency (MMIT)³⁸, which will induce remarkable phenomena of slow light.

Thirdly, we further consider coupled majorana modes (ϵ_MF ≠ 0) but adjust the detuning Δ_c from Δ_c = 0 to Δ_c = 0.5 × 10⁹ Hz. In this case, the location of the left peaks of unsymmetric Rabi splitting coincides with frequency shift induced by the exciton-pump field detuning, and then the resonant makes the coherent interaction between the QD and a couple of MFs more stronger. Figure 4(a) gives the absorption spectra with several different QD-MFs coupling strength under two detuning, i.e. Δ_MF = −0.5 × 10⁹ Hz, Δ_c = 0.5 × 10⁹ Hz, which shows more remarkable unsymmetric splitting and the intensity is also enhanced simultaneously. Figure 4(b) is the detail parts of the left peaks in Fig. 4(a). Moreover, we make a comparison between the two situations, i.e. (Δ_c = 0, Δ_MF = −0.5 × 10⁹ Hz) and (Δ_c = 0.5 × 10⁹ Hz, Δ_MF = −0.5 × 10⁹ Hz) at a pair of coupling strength β₁ = 0.05 × 10⁹ Hz and β₂ = 0.05 × 10⁹ Hz. The probe absorption spectrum shows that the bandwidth is about 8 MHz and the intensity is about 4.5 with the left sharp peaks exactly locating at Δ_s = −0.5 × 10⁹ Hz under the condition of Δ_c = 0 and Δ_MF = −0.5 × 10⁹ Hz as shown in Fig. 4(c). However, when adjusting the detuning Δ_c from Δ_c = 0 to Δ_c = 0.5 × 10⁹ Hz, one can obtain the narrower bandwidth (about 1 MHz) and the stronger intensity (about 0.9) locating at Δ_s = −1.0 × 10⁹ Hz as shown in Fig. 4(d). In this case, the sideband peak induced by coupled majorana modes coincides with sharp peaks induced by pump off-resonant Δ_c = 0.5 × 10⁹ Hz, which makes the coherent interaction of QD-MF more strong.

Figure 4

(a) The probe absorption spectra at Δ_MF = −0.5 GHz, Δ_c = 0.5 GHz, and (b) is the detail parts of the left peaks in (a). (c) The probe absorption spectrum shows a bandwidth about 8.0 MHz at Δ_c = 0 and Δ_MF = −0.5 GHz. (d) The absorption spectrum shows a bandwidth about 1.0 MHz at Δ_c = 0.5 GHz and Δ_MF = −0.5 GHz.

Moreover, we slao investigate the optical Kerr nonlinear effect of QD mediated by MFs. Figure 5(a) gives the optical Kerr coefficient (Re(χ⁽³⁾)) as a function of Δ_s under ϵ_MF ≠ 0 with the resonance detuning Δ_c = 0. In Fig. 5(a), the black curve displays the nonlinear optical Kerr spectrum without the QD-MFs coupling, the red curve gives the QD couples to one MFs with coupling strength β₁ = 0.05 GHz, the blue one is that the QD couple to a pair of MFs with coupling strength β₁ = 0.05 GHz and β₂ = 0.05 GHz under Δ_c = 0 and Δ_MF = −0.5 GHz. Figure 5(b,c) are the detail parts of the right and left peaks in Fig. 5(a). It is obvious that when the MFs emerge in the hybrid S/SR device and couple to the QD, two sharp sideband peaks will emerge in the optical Kerr spectra. The physical origin of the results are due to the coherent interaction between the QD and MFs, which makes the resonant enhancement of the optical Kerr effect in the QD. Figure 5(d) shows optical Kerr coefficient at uncoupled Majorana modes with no QD-MFs coupling, one QD-MFs coupling, and a pair of QD-MFs coupling, optical Kerr spectra also present splitting when the QD couple to MFs. The results signify that the sharp peaks in the nonlinear optical spectra may be the signature of real MFs which gives the nonlinear optical means to detect MFs.

Figure 5

(a) The optical Kerr coefficient as a function of Δ_s at coupled majorana modes (ϵ_MF ≠ 0) and the detuning Δ_c = 0. (b) and (c) are the detail parts of the right and left peaks in (a). (d) The optical Kerr coefficient at ϵ_MF = 0 and Δ_c = 0.

Switching Δ_c from Δ_c = 0 to Δ_c = 0.5 GHz, Fig. 6(a) presents the optical Kerr coefficient vs. the detuning Δ_s at coupled Majorana modes under several different QD-MFs coupling strengths, and the details are shown in Fig. 6(b,c). It is obvious that the width of splitting induced by a pair of MFs couple to the QD is larger than in the case of one MF couple to the QD. Furthermore, the width of splitting in the optical Kerr spectrum is determined by the two detuning and QD-MFs coupling strength β₂ and β₂ as shown in Fig. 6(d).

Figure 6

(a) The optical Kerr coefficient at ϵ_MF ≠ 0 and Δ_c = 0.5 GHz with several different QD-MFs coupling strength, (b) and (c) are the details in (a). (d) The width of splitting in the optical Kerr spectrum is determined by Δ_c, Δ_MF and QD-MFs coupling strength β₂ and β₂.

Discussion

We have designed a hybrid S/SR device and introduced an optical pump-probe technology to probe MFs with QDs which is very different from the current electrical method. In the previous theoretical schemes for detecting MFs with QD, QD is considered as only one resonant level with single spin state and they only consider one adjacent MF interact with the QD. In this work, we investigate a pair of MFs coupled to the QD which induces remarkable splitting in the probe absorption spectrum and nolinear optical Kerr spectrum. The symmetric and unsymmetric Rabi splitting and optical Kerr nonlinear effect of QD mediated by MFs are studied under uncoupled and coupled majorana modes, respectively. Due to QD-MFs coupling, the probe absorption spectra present the phenomenon of Majorana modes induced transparency which will induce remarkable phenomena of slow light. With adjust the exciton resonant detuning and Majorana resonant detuning, the probe absorption intensity and the peak width of splitting are enhanced significantly, and the peak width of splitting in the optical Kerr spectrum depends on the coupling strength and resonant detuning.

Compared with electrical measurement, the optical scheme for the detection of MFs have several advantage, the first one is that there is no contact between the QD and the hybrid S/SR device, thus the introduce of noises can be avoided effectively, and finally the sensitivity of the measurement will enhance observably. The second one is that nanostructures such as QD have obtained remarkable progress in modern nanoscience, which paves a way to detect MFs experimentally. Therefore, the optical detection of MFs with QD is scientific and feasible based on recent experiment. The scheme proposed here may provide potential applications in quantum computing based on MFs with optically controlled in solid-state systems.

Methods

The Heisenberg operator (ρ = S^z, S⁻, f_M) can be divided into two parts including steady-state mean value ρ₀ and small fluctuation δρ, i.e. ${S}^{z}={S}_{0}^{z}+\delta {S}^{z}$, S⁻ = S₀ + δS⁻, f_M = f_M0 + δf_M. Inseting these operators into Eqs (4–6), we then abtain the following equations

$${\partial }_{t}{S}^{z}=-{{\rm{\Gamma }}}_{1}[{S}_{0}^{z}+\delta {S}^{z}+1/\mathrm{2]}-({\beta }_{1}+i{\beta }_{2})({S}_{0}+\delta {S}^{-})({f}_{M0}^{\ast }+\delta {f}_{M}^{+})-({\beta }_{1}-i{\beta }_{2})({S}_{0}^{\ast }+\delta {S}^{+})({f}_{M0}+\delta {f}_{M})+i{{\rm{\Omega }}}_{c}[({S}_{0}^{\ast }+\delta {S}^{+})-({S}_{0}+\delta {S}^{-})]+\frac{i\mu {E}_{s}}{\hslash }({S}_{0}^{\ast }{e}^{-i\delta t}+\delta {S}^{+}{e}^{-i\delta t}-{S}_{0}{e}^{i\delta t}-\delta {S}^{-}{e}^{i\delta t}),$$

(11)

$${\partial }_{t}{S}^{-}=-(i{{\rm{\Delta }}}_{c}+{{\rm{\Gamma }}}_{2})({S}_{0}+\delta {S}^{-})+\mathrm{2(}{\beta }_{1}-i{\beta }_{2})({S}_{0}^{z}+\delta {S}^{z})({f}_{M0}+\delta {f}_{M})-2i{{\rm{\Omega }}}_{c}({S}_{0}^{z}+\delta {S}^{z})-\frac{2i\mu {E}_{s}}{\hslash }{e}^{-i\delta t}({S}_{0}^{z}+\delta {S}^{z})+\hat{\tau }(t),$$

(12)

$${\partial }_{t}{f}_{M}=-(i{{\rm{\Delta }}}_{MF}+{\kappa }_{M}/\mathrm{2)(}{f}_{M0}+\delta {f}_{M})+({\beta }_{1}+i{\beta }_{2})({S}_{0}+\delta {S}^{-})+\hat{\xi }(t),$$

(13)

To solve Eqs (11–13), we get two equation sets. The first one is steady-state mean equation set as follows

$${{\rm{\Gamma }}}_{1}({S}_{0}^{z}+1/\mathrm{2)}+({\beta }_{1}+i{\beta }_{2}){S}_{0}{f}_{M0}^{\ast }+({\beta }_{1}-i{\beta }_{2}){S}_{0}^{\ast }{f}_{M0}=i{{\rm{\Omega }}}_{c}({S}_{0}^{\ast }-{S}_{0}),$$

(14)

$$(i{{\rm{\Delta }}}_{c}+{{\rm{\Gamma }}}_{2}){S}_{0}+\mathrm{2(}{\beta }_{1}-i{\beta }_{2}){S}_{0}^{z}{f}_{M0}=2i{{\rm{\Omega }}}_{c}{S}_{0}^{z},$$

(15)

$$(i{{\rm{\Delta }}}_{MF}+{\kappa }_{M}/\mathrm{2)}{f}_{M0}-({\beta }_{1}+i{\beta }_{2}){S}_{0}=0,$$

(16)

which determines Eq. (8). The second one is the fluctuation equation set which is

$$\begin{array}{ccc}\delta {\dot{S}}^{z} & = & -\,{{\rm{\Gamma }}}_{1}\delta {S}^{z}-({\beta }_{1}+i{\beta }_{2})({S}_{0}\delta {f}_{M}^{+}+{f}_{M0}^{\ast }\delta {S}^{-})-({\beta }_{1}-i{\beta }_{2})({S}_{0}^{\ast }\delta {f}_{M}+{f}_{M0}\delta {S}^{+})\\ & & +i{{\rm{\Omega }}}_{c}(\delta {S}^{+}-\delta {S}^{-})+\frac{i\mu {E}_{s}}{\hslash }[{S}_{0}^{\ast }{e}^{-i\delta t}-{S}_{0}{e}^{i\delta t}],\end{array}$$

(17)

$$\delta {\dot{S}}^{-}\,=\,-\,(i{{\rm{\Delta }}}_{c}\,+\,{{\rm{\Gamma }}}_{2})\delta {S}^{-}\,+\,{\theta }_{0}({\beta }_{1}\,-\,i{\beta }_{2})\delta {f}_{M}\,+\,\mathrm{2[}{f}_{M0}({\beta }_{1}\,-\,i{\beta }_{2})\,-\,i{{\rm{\Omega }}}_{c}]\delta {S}^{z}\,-\,\frac{i\mu {w}_{0}{E}_{s}}{\hslash }{e}^{-i\delta t},$$

(18)

$$\delta {\dot{f}}_{M}=-(i{{\rm{\Delta }}}_{MF}+{\kappa }_{M}/\mathrm{2)}\delta {f}_{M}+({\beta }_{1}+i{\beta }_{2})\delta {S}^{-},$$

(19)

Solving Eqs (17–19), we obtain Eqs (9 and 10).