Introduction

The emergence of physical degrees of freedom and their easy manipulation has led to corresponding fields of electronics, such as spintronics1, valleytronics2, and plasmonics3. As a unique degree of freedom appearing only at the domain boundary between two different topological phases, a topological charge4 can give rise to topological electronics. For topological electronics, whereby information is carried by the topological charge through the topological domain boundary5,6, at least two distinct topological phases should be accessible and controllable within a system. In this regard, a gap-tunable graphene-like electronic structure7,8 is an ideal candidate for topological electronics applications. It has been suggested that various topological phases can be hosted by opening the band-gap of a Dirac cone via spin-orbit coupling (SOC) or symmetry-breaking; the quantum spin Hall (QSH) phase can be induced by SOC9, the quantum valley Hall (QVH) phase by breaking the sublattice symmetry10, and the quantum anomalous Hall phase by breaking the time-reversal symmetry11.

The maximum band-gap tunability of a Dirac cone, which is essential for topological electronics but barely achievable in graphene12, can be realized in a (111)-oriented BaBiO3 bilayer (BBL) oxide heterostructure. The confluence of oxide heterostructures13,14,15, Dirac materials16, and topological quantum matters17,18,19 produces a graphene analogue with a tunable band-gap, which links directly to the tunable topological phase. As shown in Fig. 1(a), in the crystal structure of the BBL, the Bi atom forms a buckled honeycomb network. Considering the Bi4+ (6s1) configuration of BaBiO3, the half-filled 6s-orbital in the honeycomb lattice inherently produces a Dirac cone at points K and K′ in the hexagonal Brillouin zone. The large SOC stems from the strong hybridization between the neighboring Bi 6s- and 6p-orbitals. Here we note that the bulk BaBiO3 was reported to be a three-dimensional topological insulator due to the large SOC of the Bi 6p-orbitals19. Importantly, the abundant order parameters of the sandwiching oxide perovskite materials can break various symmetries of BBL, allowing it to possess various topological phases.

Figure 1
figure 1

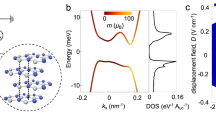
Graphene analogue and various topological phases in BaBiO3 bilayer (BBL) heterostructures. (a) Atomic configuration of the B-site atoms in the BaMIO3/BBL/BaMIIO3 heterostructure. (b) Massless/massive Dirac cones and the corresponding topological phases in the BBL heterostructure as a function of spin-orbit coupling (SOC) (λSOC) and the sublattice potential difference (Δ). The electronic band structure of the symmetric BaZrO3/BBL/BaZrO3 heterostructure (c) without and (d) with SOC, and (e) the topologically protected edge state of the quantum spin Hall (QSH) phase along the zigzag edge. The band structure of the asymmetric BaZrO3/BBL/BaHfO3 heterostructure (f) without and (g) with SOC, and (h) the Berry curvature that is alternating at each valley and indicating the quantum valley Hall (QVH) phase.

Full size image

Results

Various topology in oxide heterostructures

Specifically, BaMIO3/BBL/BaMIIO3 heterostructures stacked along the [111]-direction are considered (Fig. 1(a)). The simple design principle applied for construction of the target system is that BBL provides a graphene-like low-energy electronic degree of freedom, and the sandwiching perovskite oxides, BaMIO3 and BaMIIO3, determine the symmetry of the BBL. Therefore, the topological phase and band-gap of the Dirac cones rely completely on the choice of the MI and MII atoms. Given the wide variety of choice as MI and MII atoms, rich physics, including non-trivial band topology, is accessible in this oxide heterostructure platform.

When the MI and MII atoms are of the same species, and their perovskite form, BaMI,IIO3, has a para-electric, non-magnetic insulating phase, the BBL has the full space-group symmetry of the buckled honeycomb lattice and time-reversal symmetry. Subsequently, a gapless Dirac cone, the fundamental building block in this work, appears. After containing the SOC, the Dirac cone acquires a mass-gap and the QSH phase emerges, which exactly realizes the Kane-Mele model9. Alternatively, if we choose different MI and MII atoms while preserving the time-reversal symmetry, we can selectively break the inversion symmetry of the BBL heterostructure. The break in the inversion symmetry of the BBL resulting from using two different neighboring oxides is equivalent to the sublattice symmetry breaking of the buckled honeycomb lattice. As a result, the Dirac cone acquires a sublattice-dependent mass-gap, and the system adopts the QVH phase10. With no inversion symmetry, SOC can exhibit extra valley-dependent spin splitting at the gapped Dirac cone and introduce spin-valley coupling, which is frequently seen in the monolayer transition metal dichalcogenide series20. These features are summarized in Fig. 1(b), and the corresponding ab-initio calculations are shown in Fig. 1(c–h).

Electronic structures

For the symmetric BBL configuration where MI = MII = Zr, the electronic structures without and with SOC are calculated in Fig. 1(c),(d), respectively. Gapless linear band dispersion appears inside the large band-gap of the sandwiching oxide, BaZrO3, and the low-energy band structure is governed by the Bi 6s-orbital Dirac cone (Fig. 1(c)). When SOC is included, a band-gap of 79 meV opens at the Dirac point (Fig. 1(d)); opening of a band-gap by SOC in an otherwise gapless Dirac cone indicates the presence of a Kane-Mele type topological insulator. The unexpectedly large SOC-induced gap in the s-orbital system is attributed to the strong Bi 6s-6p hybridization and the large atomic SOC of the Bi 6p-orbital (for details on the tight-binding analysis and SOC, see Supplementary Information). The topologically protected edge state, shown in Fig. 1(e), of the ribbon geometry with the zigzag edge confirms the QSH phase of the symmetric BBL heterostructure via the bulk-boundary correspondence. The same QSH phase of the symmetric configuration is attainable with other sandwiching perovskite compounds, including a Sr-based heterostructure in which all of the Ba atoms are replaced by Sr atoms. These are listed in Table 1, and the band-gap ranges from 45 to 100 meV. Therefore, the QSH phase in the symmetric BBL configuration is detectable and usable at room temperature.

Table 1 Lattice parameters and QSH gap in symmetric heterostructures.
Full size table

Figure 1(f),(g) depict the electronic structures without and with SOC, respectively, for the asymmetric BBL configuration where MI = Zr and MII = Hf. The structural inversion asymmetry induced by sandwiching with different oxides produces the potential difference at each sublattice site of the buckled honeycomb structure, and results in a QVH phase with a direct band-gap of 0.92 eV at the Dirac point (Fig. 1(f)). In the asymmetric BBL configuration, the band topology is characterized by the valley-Chern number, and the QVH phase is verified by calculating the valley-contrasting Berry curvature10 as shown in Fig. 1(h). The Berry curvature at each K and K′ valley has the opposite sign, leading to the non-zero valley-Chern number. As SOC is turned on, extra valley-dependent spin splitting at both the conduction and valence band edges occurs by 103 and 29 meV, respectively (Fig. 1(g)). In addition to the usefulness of the QVH phase for topological electronics, this interesting spin-valley coupling might be available for spin-valleytronics applications20,21; near K and K′, both valley-dependent Zeeman-type and valley-independent Rashba-type spin splitting occur on the out-of-plane and in-plane spin components, respectively (see Supplementary Information Fig. S2).

Ferroelectric control of topological phases

Having revealed that two distinctive topological phases, QSH and QVH, take place in the same framework, the BBL heterostructure still has room for improvement in terms of topology-tunability; the QSH phase still cannot be converted into the QVH phase and vice versa within one system. Recalling that the topological phase of the BBL heterostructure is governed by its symmetry, topology-control is synonymous with symmetry-control in this system. Therefore, introducing a symmetry-breaking order parameter in the neighboring perovskite oxide makes it possible to control the topology of the BBL heterostructure. Because the corresponding symmetry that distinguishes the QSH and QVH phases is the spatial inversion, BBL sandwiched by ferroelectric perovskite oxides provides a way to control the inversion symmetry, and ultimately switch the QSH and QVH phases.

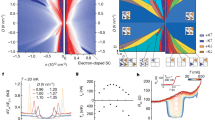
By sandwiching the well-known ferroelectric BaTiO3 with the [111] polarization direction, we can construct a BaTiO3/BBL/BaTiO3 heterostructure as a unified system hosting and controlling both the QSH and QVH phases. Depending on the relative polarization direction of the BaTiO3 on either side of the BBL, the inversion symmetry can be either conserved or broken; if the polarization direction is the opposite (same), the inversion symmetry of the BBL heterostructure is conserved (broken). As a result, the QSH (QVH) phase with a band-gap of 108 meV (1.17 eV) arises within the anti-parallel (parallel) polarization configuration, as shown in Fig. 2(a),(b)). Moreover, by developing a ferroelectric domain boundary, a topological domain boundary is induced, in which a topologically protected edge state emerges and the topological charge flows. Suppose that we prepare a BaTiO3/BBL/BaTiO3 heterostructure that initially has a parallel polarization configuration. As the polarization of the upper BaTiO3 layer starts to be flipped using an atomic-force microscope (AFM) tip and a ferroelectric domain boundary is generated, the topological domain boundary between the QSH and QVH phases develops simultaneously (see Fig. 2(c)). This controllability22 enables us to manipulate the conducting path of the topological charge in a non-volatile, reconfigurable way, which is an important operation in topological electronics.

Figure 2
figure 2

Ferroelectric control between QSH and QVH phases. Ferroelectric switching alters the topological phase of the BaTiO3/BBL/BaTiO3 heterostructure: (a) anti-parallel and (b) parallel polarization correspond to the QSH and QVH phases, respectively. (c) The ferroelectric domain boundary controlled using the atomic force microscope (AFM) tip generates the QSH/QVH topological domain boundary.

Full size image

Discussion

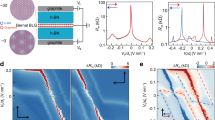
A major premise in this work is the Bi4+ charge state in the buckled honeycomb lattice; the fundamental building block—the 6s-orbital Dirac cone—and the subsequent topological phases hinge entirely on it. However, Bi4+ is unstable in bulk BaBiO3, in which the charge ordering of Bi3+ and Bi5+ is accompanied by breathing instability of the BiO6 octahedron, and the Bi3+ and Bi5+ planes alternate along the [111]-direction23. If the Bi4+ charge state is unstable in the BBL heterostructure, the QSH phase seen in the symmetric configuration becomes unstable and transforms into the QVH phase by spontaneously breaking the sublattice symmetry. Therefore, it is important to verify the robustness of Bi4+ and the graphene-like electronic structure in the BBL heterostructure against the charge ordering instability. We applied a small external electric field along the [111]-direction of the BaZrO3/BBL/BaZrO3 slab geometry to examine whether a small perturbation can trigger the charge ordering and induce the QVH phase abruptly. As shown in Fig. 3(a), the QSH band-gap of 75.7 meV decreases continuously, closes at εc = 26 mV/Å, and re-opens as the field strength increases. At the gap-closing point, band inversion occurs and the topology of the system changes from the QSH to the QVH phase. Consequently, unlike the bulk BaBiO3, the Bi4+ charge state and QSH phase in the symmetric configuration of the BBL heterostructure remain intact under a small external perturbation. Recent experiments examining BaBiO3 thin films showed that the charge ordering instability is suppressed as the film thickness decreases24, which is consistent with our result.

Figure 3
figure 3

Stability of QSH phase and design of topological electronic field effect transistors. (a) The stability of the QSH phase in the symmetric BBL heterostructure is tested by applying a vertical electric field. (b) The single-gated transistor and (c) edge states as a function of the gate electric field are depicted schematically. (d) For a large gate electric field, the spin-momentum locked QSH edge states appear at both sides of the QSH/QVH boundary. (e) The double-gated transistor is sketched, and (f) the various topological domain boundaries are tuned by the gate electric fields. (g) The corresponding topological edge configurations are shown. The grey area in (c) and (f) indicates the strong edge overlapped region.

Full size image

This stability test revealed one more appealing aspect; the Bi4+ charge state is not only sufficiently stable to sustain multiple Dirac cones, but is also susceptible to easy manipulation of the band-gap and topological phase by a small electric field. The QSH gap is closed by an external field of εc = 26 mV/Å and the band topology is switched to the QVH phase at greater field strengths. The large buckling angle in the BBL honeycomb lattice and the latent Bi3+/5+-tendency seem to be responsible for the easy tunability, and make the system a potential platform for topological electronics via the electric field. Taking advantage of the easy controllability of the band-gap and topology of the BBL heterostructure, we designed a topological electronic field-effect-transistor25, as shown in Fig. 3(b–g). The single-gated transistor sketched in Fig. 3(b) can develop the QSH/QVH domain boundary, possibly leading to the QSH edge state when the gate electric field εz > εc. Considering the finite width W of the gate electrode, the edge states located at both sides of the topological domain boundary can overlap if the band-gap of the QVH phase induced by εz is small. Given that the penetration length of the edge state into the insulating bulk is \(\frac{{v}_{F}}{{E}_{g}}\), where v F is the Fermi velocity of the Dirac cone (3.55 × 105 m/s in the BBL heterostructure) and Eg is the band-gap, strong edge overlap occurs when \(\frac{W}{2}\lesssim \frac{{v}_{F}}{{E}_{g}}\). For example, if W = 50 nm and εc < εz ≤ 29.2 mV/Å, the QSH edge states on both sides easily interact via the shallow-gapped bulk region, hampering its ability to carry a topological charge through the topological domain boundary. Therefore, a gate electric field well above εc can host the spin-momentum-locked QSH edge states (see Fig. 3(c),(d)).

The double-gated system sketched in Fig. 3(e) can give rise to various topological domain boundary configurations and their corresponding topological edge states. As well as the QSH/QVH boundary, the topological domain boundary between two different QVH phases, whose non-zero valley-Chern numbers have the opposite sign, also appears depending on the gate electric fields ε1z and ε2z (Fig. 3(f)). Again, due to the finite width of the two gate electrodes W1 and W2, a strong edge-overlapped region exists, and is shown in grey in Fig. 3(f). With |ε1z| < εc < |ε2z| (|ε2z| < εc < |ε1z|), the double-gated transistor behaves in the same way as the single-gate transistor, and the strong edge-overlapped region is determined by \(\frac{{W}_{1}}{2}\lesssim \frac{{v}_{F}}{{E}_{1g}}\) \((\frac{{W}_{2}}{2}\lesssim \frac{{v}_{F}}{{E}_{2g}})\). When both gate electric fields exceed εc and are aligned in parallel, the QVH phase is formed in a region whose effective width is W1 + W2; thus, the condition for the strong edge overlap between the QSH edge states becomes \(\frac{{W}_{1}+{W}_{2}}{2}\lesssim \frac{{v}_{F}}{{E}_{1g}}+\frac{{v}_{F}}{{E}_{2g}}\). Interestingly, two gate electric fields exceeding εc but with an anti-parallel alignment develop two QVH phases possessing the opposite valley-Chern numbers. As a result, the valley-momentum-locked QVH edge states appear along the inner QVH domain boundary26,27, together with the QSH edge states along the outer QSH/QVH boundary. The existence and position of various non-trivial edge states can be controlled by the gate electric fields in the double-gated transistor (Fig. 3(g)). In an array of multiple topological electronic transistors based on the BBL heterostructure, we can tailor the conducting path that carries two different topological charges28.

In conclusion, we show that the hetrostructure of a (111)-oriented BaBiO3 bilayer sandwiched between perovskite oxides can host QSH and QVH phases with the choice of sandwiching materials, and is therefore a promising platform of topological electronics. Although the overall discussion focuses on controlling the inversion symmetry, a BBL heterostructure sandwiched by various ferroic perovskite oxides will likely serve as a general scheme for hosting many controllable topological phases. For example, by introducing a ferromagnetic sandwiching oxide, we can break the time-reversal symmetry of the BBL in two different ways. With parallel ferromagnetic moments on both sides, the BBL honeycomb lattice is subject to a constant Zeeman field, possibly generating the quantum anomalous Hall phase by breaking the time-reversal symmetry4. For the anti-parallel ferromagnetic moments, a sublattice-dependent staggered Zeeman field arises, leading to the so-called quantum spin-valley Hall phase by breaking both the time-reversal and inversion symmetries but conserving the composite of the two symmetries29. For the BBL sandwiched by multi-ferroic perovskite oxides, we can control both the spatial inversion and time-reversal symmetries simultaneously30. The potential to make a three-dimensional integrated superlattice composed of various topological compartments makes the BBL heterostructure even more fascinating.

Methods

First-principles calculations

The first-principles calculations were performed using the density functional theory with projector augmented wave potentials and the Perdew-Burke-Ernzerhof exchange correlation functional as implemented in VASP code31,32. The plane-wave energy cutoff was set at 400 eV, and 12 × 12 × 1 mesh was used for momentum space sampling. The atomic structures were relaxed with the force criteria of 0.005 eV/Å. The wannier90 code was used to construct the maximally-localized Wannier function33, in which four Bi s-projectors (including spin components) were used to reproduce the band structures near the Fermi level. The Berry curvature was calculated with the linear response Kubo formula, and the tight-binding Hamiltonian of strip geometry was constructed using the obtained Wannier functions and hopping parameters.

Data Availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.