Introduction

The fractional accuracy on spectroscopic measurements on atoms has reached the few parts in 1018  1; the same quantity in experiments on molecules is worse by more than three orders of magnitude2,3,4,5,6,7. This difference is due to the richer internal structure of molecules that makes cooling and detection more complicated than in atoms. Nevertheless, the internal structure and symmetry of molecules, and their strong intramolecular fields can enable totally new measurements. Recent experiments on ThO yielded the most sensitive measurement to date of the electron electric dipole moment2. The upper limit found in the 10−29 e cm range constrains T-violating physics at the TeV energy scale, comparable to the energy scales explored directly at the Large Hadron Collider. In other experiments, the assessments in the laboratory of the variation of fundamental constants based on molecular spectroscopy3,4 achieve a level of sensitivity similar to astronomical observations looking back in time several billion years. Still other experiments are probing energy differences in enantiomers of chiral species5, testing quantum electrodynamics6, and searching for a fifth force7.

The mid IR is a natural spectral region for high-resolution spectroscopic studies on molecules because it corresponds to the typical energy range of fundamental rovibrational transitions, characterized by strong linestrenghts and Hz-level natural linewidths. In order to achieve a level of precision typical of atomic physics experiments, one needs a cold molecular sample combined with state-of-the-art light sources in the mid IR8. Since 2014, cold molecules technology has considerably advanced. YO9 and CaF10 were laser cooled and SrF was trapped in a three-dimensional magneto-optical trap11. Prehn et al.12 applied optoelectrical cooling to formaldehyde, achieving temperatures as low as 0.5 mK with 107−8 molecules/cm3 densities. Very recently, Cheng et al.13 reported on an ammonia fountain that enables, in principle, measurements with sub-Hz linewidths; and Truppe et al.14 laser cooled CaF below the Doppler limit, to 50 μK.

However, photonics in the mid IR remains challenging. Coherent sources for precision spectroscopy must feature sufficient intensity, very narrow linewidth, high frequency stability, and an absolute frequency traceability against the primary frequency standard. Continuous wave optical parametric oscillators can match these requirements only below 5 μm but are difficult to operate15, while difference frequency generation processes suffer from low emitted powers. Room-temperature quantum cascade lasers (QCLs) are a promising technology. They cover the whole 3–25 μm range and yield mW-to-W power levels16. They have very narrow intrinsic linewidths17 but are particularly sensitive to driver current noise18. However, with proper control, QCLs have yielded linewidths in the sub-Hz–kHz range19,20,21. An open issue in using QCLs to perform precision spectroscopy is that most of a QCL emitted power has to be used to realize an up-frequency conversion in order to compare the QCL frequency to the frequency standard20,21,22.

This transfer of the frequency standard to the mid IR is generally achieved in two steps. First, an optical frequency comb bridges the gap from the microwave to the near IR. Then, a non-linear frequency conversion process is used to reach the mid IR. The accuracy of the IR frequencies depends critically on the stability of the comb repetition rate. The recent rise of frequency dissemination by optical fibres represents a radical improvement23. While RF oscillators disciplined by the Global Positioning System (GPS) can achieve 10−14 stability and accuracy only after tens of thousands seconds integration times, the same stability and accuracy are reached in 1 second by using an optical dissemination of the frequency standard, and the intrinsic uncertainty of the disseminated clock is reached with short interaction times3,21,23.

Here we demonstrate a laser technology that can be extended to the whole mid IR range between 1 and 10 μm with state-of-the-art metrological features. We demonstrate its performance by measuring a vibrational transition around 6 μm on a highly-excited, metastable state in carbon monoxide with kHz-level accuracy. The measurement is performed on a molecular beam with a density of about 108/cm3 in a selected quantum state, similar to what is currently obtained in state-of-the-art setups for cold molecules. Our system is based on three pillars.

First, the frequency reference to the primary standard is transferred by an ultra stable laser at 1542 nm sent over the Italian fibre-link network24. This network connects several laboratories all over the Italian territory, and it is part of a continental metrological network that is currently under construction.

Second, difference frequency generation in an orientation patterned (OP) GaP crystal allows us to bridge the gap between near and mid IR. OP-GaP provides a reasonable efficiency25 and a high transparency over the whole 1–10 μm range, with an absorption coefficient always below 0.5 cm−1  26. Unlike competing crystals like OP-GaAs, its band edge lies in the visible region, so two-photon absorption is negligible above 1 μm (for comparison, two-photon absorption in OP-GaAs prevents pumping below 1.5 μm)27. This allows OP-GaP to be pumped directly with powerful lasers at 1 μm, and proper domain patterning period provides the required tuning parameter needed to cover the material’s full transparency range.

Third, a quantum cascade laser produces the mid IR radiation, which is almost entirely used for spectroscopy and not for frequency control.

Optical Setup

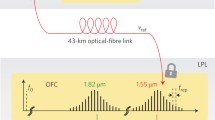
Figure 1 shows the main features of the metrological chain to control a QCL. We lock two near-IR lasers to a frequency comb whose repetition rate is referenced and stabilized using the fibre link. The light of these two lasers is mixed in an OP-GaP crystal to generate the difference of their frequency, which lies in the mid IR. Finally, such mid IR radiation is used to phase-lock the QCL.

Figure 1
figure 1

The left part of the figure shows the Italian fibre link network, blue line, with network nodes in red. At LENS/University of Florence (LENS in the following for brevity), the ultra stable laser at 1542 nm locks the repetition rate of a frequency comb. We measure the beat notes of two near-IR lasers against the frequency comb and keep their frequency difference constant with an indirect locking scheme to cancel out the comb noise contribution29. The two lasers are combined in an OP-GaP crystal to generate mid-IR light, to which we lock a quantum cascade laser. (The map is obtained on the basis of ©OpenStreetMap contributors (www.openstreetmap.org) licensed under the Creative Commons Attribution-ShareAlike 2.0 license (CC BY-SA) https://creativecommons.org/licenses/by-sa/2.0/. The basis was then modified to fit our figure and we took no care to maintain proportions or accuracy).

Full size image

The fibre link network carries the light of an ultra stable laser that is kept at a frequency of 194399996000000.00(4) Hz (i.e. around 1542 nm), where the uncertainty is directly related to that of the Cs fountain. The laser frequency is referenced to the Italian timescale, generated at the Italian Metrological Institute (INRIM) in Turin. This signal reaches several relevant locations on the national territory: the Institute for Radioastronomy in Medicina (535 km from INRIM), the European Laboratory for Nonlinear Spectroscopy, LENS, in Sesto Fiorentino (642 km), Rome (994 km), and the Italian-French border (150 km). In addition, a timestamp signal referenced to the Italian timescale reaches the financial district in Milan (279 km). During 2017, the fibre network will be extended to the National Institute for Optics INO in Arcetri (662 km), to CNR labs in Pozzuoli (1306 km), to the Galileo Precise Time Facility in Fucino (1134 km), to the Space Geodesy Center in Matera (1684 km), and finally to the French metrological institute LNE-SYRTE in Paris.

A series of bidirectional erbium-doped fibre amplifiers compensate for the almost 200-dB optical losses of the link between INRIM and LENS24. To phase-stabilize the fibre link, part of the radiation at 1542 nm travels back to INRIM on the same fibre, after being retro-reflected at LENS. The photon round-trip, over 1200 km, limits the bandwidth of the phase-lock loop. Thus the laser at 1542 nm has a large phase noise in the short term (<5 ms), while it has a stability of 1 × 10−14 at 1 s and an accuracy of 2 × 10−16; these performances have been assessed by measuring the absolute frequency of the 1542-nm laser on two independent optical combs referenced to the same H-maser23. The noise generated by the optical link does not affect the uncertainty of the delivered signal within parts in 1019  24.

At LENS, we phase-lock a diode laser to the incoming radiation, replicating the stability of the link laser and boosting the optical power at a suitable level for referencing a frequency comb. An intra-cavity electro-optic modulator phase-locks the repetition rate f rep of a commercial frequency comb to the 1542-nm light, with a bandwidth of approximately 300 kHz. We choose the lock frequency so that the repetition rate is 100 MHz when the incoming radiation is at the nominal frequency value. The carrier-envelope offset frequency f 0 of the comb is stabilized to an RF frequency standard. The residual noise of the stabilized link, which scales with the link length28, dominates the phase-noise of the comb.

In an OP-GaP crystal we generate the difference frequency of two mid IR lasers, a Nd:YAG MOPA system at 1064 nm with a linewidth of 1 kHz and operated at a power of about 5 W (pump), and a diode laser at 1220–1320 nm delivering about 30 mW (signal). The quasi phase matching condition is tuned between 5.8 and 6.0 μm (idler wavelength) by changing the temperature of the OP-GaP crystal between 30 and 150 °C. Two fast InGaAs photodiodes detect the beat notes of both lasers to the closest teeth of the frequency comb with a minimum signal-to-noise ratio of 25 dB on a 100 kHz bandwidth. We refer to these beat notes as \({f}_{{\rm{b}}:{\rm{pump}}}\) and \({f}_{{\rm{b}}:{\rm{signal}}}\), and we refer to the absolute frequencies of the two lasers as \({\nu }_{{\rm{pump}}}\) and \({\nu }_{{\rm{signal}}}\). The pump laser is phase-locked directly to the closest comb tooth on a bandwidth of 700 Hz. Figure 2 shows the phase noise of the beat note \({f}_{{\rm{b}}:{\rm{pump}}}\). Instead of locking the signal laser directly to the comb, we stabilize the difference frequency \({\nu }_{{\rm{pump}}}-{\nu }_{{\rm{signal}}}\) with an indirect lock of the signal laser to the pump. For this, we use the frequency comb to bridge the gap between the two lasers but we reject its noise contribution by proper processing of \({f}_{{\rm{b}}:{\rm{pump}}}\), \({f}_{{\rm{b}}:{\rm{signal}}}\), and f 0 29.

Figure 2
figure 2

Phase noise of various components of the frequency locking chain. The phase noise of the free running QCL is shown in black. The noise on the fibre link is shown in blue. The error signal of the phase-lock loop for the pump laser is shown in green. The expected phase noise of the phase-locked QCL is shown in red and is obtained by scaling the phase noise of the pump laser, following the virtual beat note scheme.

Full size image

To implement this indirect locking scheme, we subtract f 0 from each beat note using analog mixers, obtaining \({\overline{f}}_{{\rm{b}}:{\rm{pump}}}\) and \({\overline{f}}_{{\rm{b}}:{\rm{signal}}}\). Thus, the absolute frequencies of the two lasers can be written as \({\nu }_{{\rm{pump}}}={N}_{{\rm{pump}}}{f}_{{\rm{rep}}}+{\overline{f}}_{{\rm{b}}:{\rm{pump}}}\) and \({\nu }_{{\rm{signal}}}={N}_{{\rm{signal}}}{f}_{{\rm{rep}}}+{\overline{f}}_{{\rm{b}}:{\rm{signal}}}\), where N pump = 2816363 and N signal = 2302371 are the comb teeth used for the beat notes. A 14-bit direct digital synthesizer and a mixer generate the signal \({\overline{f}}_{{\rm{b}}:{\rm{signal}}}-({N}_{{\rm{signal}}}/{N}_{{\rm{pump}}}){\overline{f}}_{{\rm{b}}:{\rm{pump}}}\). This signal is phase-locked to a radio frequency reference and it feeds back the signal laser on a bandwidth exceeding 200 kHz. The finite number of digits of the digital synthesizer generates a bias of about 1 Hz in the frequency difference. However, this is calculated and corrected in the final results.

Finally, we phase lock the QCL to the difference frequency of the two mid IR lasers. 100 μW radiation from the QCL is enough to produce a beat note with good signal-to-noise ratio, suited for a robust phase lock. Therefore, almost all the QCL output power is available for spectroscopy. This is a big advantage with respect to those methods that reference the QCL frequency by up-conversion, which typically require over 10 mW of QCL power20,21,30.

We analyzed the phase noise power spectral density (PSD) of every step of the chain to characterize the metrological properties of the mid IR light. The link noise (shown in blue in Fig. 2) is derived from independent measurements23 and is re-scaled to the relevant spectral region. We estimate the residual noise of the pump laser at closed phase-lock-loop (PLL) (green trace in Fig. 2) to be limited by the comb noise within the PLL bandwidth of 700 Hz. We expect the phase noise PSD of the mid IR radiation produced in the OP-GaP crystal to follow that of the pump laser scaled by a factor \({\mathrm{(1}-{N}_{s}/{N}_{p})}^{2}\), which corresponds to a 15-dB noise reduction, because the noise introduced by the PPL of the indirect locking scheme is negligible. We phase lock the QCL to this mid IR radiation with a 300-kHz bandwidth PLL. The noise of this PLL is shown in gray in Fig. 2. When the phase-lock chain is operating, the phase noise of the QCL is reduced by 11 decades at 1 Hz, 7 decades at 10 Hz, and by over four decades at 10 kHz (black and red traces for free-running and locked, respectively). Hence, we infer that the QCL linewidth is limited by the Nd:YAG laser and that the QCL long term stability and accuracy reflects reliably the performance of the Cs fountain. Finally, we remark that QCL linewidth and jitter at the kHz level can be further improved by referencing the frequency comb to an ultra narrow optical-link-disciplined laser around the Nd:YAG frequency.

Measurement of Molecular Frequencies

We prove the versatility of our setup by measuring a vibrational transition on a slow (318 m/s) molecular beam of highly-excited, metastable CO molecules, in a triple resonance experiment. Most of the QCL power can be coupled to the molecular beam, i.e. about 10 mW. For a typical transition dipole moment of 0.05 debye, this power corresponds to a Rabi frequency of some MHz for a beam waist of 1 mm, which are comfortable numbers for many experiments.

The metastable \({a}^{3}{\Pi }_{1}\), \(v=0\), \(J=1\), + state is prepared from the ground state with a pulsed laser at 206 nm (1 mJ, 150 MHz bandwidth) (see Methods). The QCL drives the vibrational transition to the \(v=1\), \(J=1\), − state. From there, the molecules are detected by multiphoton resonance-enhanced ionization. The experiment runs at 10 Hz. The stability and robustness of this triple resonance setup allows for rapid scans yielding high signal-to-noise ratios. A 25-minutes scan yields a Doppler-broadened absorption profile with a FWHM of 900 kHz, as the one shown in Fig. 3, which is already about two orders of magnitude narrower than the best value reported in the literature (±90 MHz)31. We acquired 22 scans over a few days for a total measurement time of 9 hours. This set of data determines the line center of the chosen vibrational transition on the metastable excited state with an uncertainty of 3 kHz as 51399115447 kHz—an improvement of more than 4 orders of magnitude on ref.31. The relative uncertainty of 6 × 10−11 is mainly due to systematic effects to which the QCL frequency uncertainty and linewidth contributes with 2 × 10−14 at worst.

Figure 3
figure 3

Top: a typical vibrational absorption spectrum on the \({a}^{3}{\prod }_{1}\) metastable state of CO measured in about 25 minutes. The transition \(|v=\mathrm{1,}\,J=\mathrm{1,}-\rangle \leftarrow |v=\mathrm{0,}\,J=\mathrm{1,}+\rangle \) shows a width of 900 kHz. A Voigt fit of the data (blue line) yields an uncertainty of 3 kHz on the center frequency. Bottom: sketch of the molecular beam apparatus used for the measurement. The beam is generated by a pulsed valve operated at 10 Hz. CO molecules are skimmed, excited into the metastable state by a UV laser at 206 nm, interact with the mid IR laser, and are finally detected by resonance-enhanced multiphoton ionization. Ions are collected on a microchannel plates detector. Right: level diagram of the states involved in the triple resonance scheme.

Full size image

Conclusions

We described a method to trace the frequency of an IR laser in the range from 1 to 10 μm with state-of-the-art metrological characteristics. Our frequency locking method needs only a little fraction of the laser power in the mid IR, leaving the rest available for spectroscopy. We use a QCL as a light source in the mid IR. The range below 3 μm, where QCLs are not available, can be covered using various commercially-available solid state lasers and very efficient non-linear crystals. Thus, our setup extends high-resolution, accurate frequency measurements to the whole molecular fingerprint region.

It has been suggested that the simultaneous monitoring of atomic and molecular transitions in various laboratories around the world can shed light on topological defect dark matter32. The fibre link network that is being developed on European scale, together with methods like the one presented here can contribute to such investigations. Moreover, the fibre network together with state-of-the-art mid IR photonics and innovative techniques of molecular beam manipulation brings atomic-level accuracies within reach. In particular, the 10−16 accuracy allowed by the fibre link can become the standard accuracy for measurements in the mid IR (~1013 Hz), when molecular cooling techniques will allow for 1-second interaction times.

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Methods

Mid IR light source

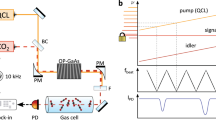
We mix 5 W at 1064 nm from a Nd:YAG laser (InnoLight GmbH, Mephisto MOPA 55 W, \({\rm{\Delta }}\nu \sim 1\) kHz over 100 ms) with 30 mW at 1301 nm from an extended-cavity tunable diode laser (Toptica Photonics AG, DL PRO, \({\rm{\Delta }}\nu \sim 100\) kHz) in a temperature-stabilized OP-GaP crystal (BAE System, Inc.) to obtain about 60 μW of light at 5.8 μm. The OP-GaP crystal is 24.6 mm long and has a patterned period of 24 μm in a 400 μm thick layer. We overlap the two near IR lasers with a dichroic mirror and focalize them on the crystal with a f = 50 mm plano-convex lens. A Germanium window separates the pump and the signal beams from the idler. The pump beam is vertically polarized (along the [001] crystallographic axis), the signal is horizontal ([110]), and they yield a horizontally polarized idler radiation. The idler power is boosted by phase locking a temperature-stabilized QCL (Alpes Laser SA) to it, which emits 10 mW at 5.8 μm. The beat note between the idler and 100 μW of the QCL radiation is detected by a thermoelectrically cooled HgCdTe photodiode with 200 μm active area (Vigo System S. A., PVI-4TE-5/MIP). The beat note has a signal-to-noise ratio of about 30 dB (on a 100 kHz bandwidth) and feeds a phase lock loop that controls the QCL current with a 300-kHz bandwidth.

Locking chain

The carrier-envelope offset frequency f 0 of a commercial frequency comb (Menlo Systems GmbH, FC1500-100-WG) is stabilized at 20 MHz using a radio-frequency reference signal delivered by a GPS-disciplined rubidium oscillator. The repetition rate frequency f rep is phase-locked to the reference light at 1542 nm using an intra-cavity electro-optic modulator on a bandwidth of approximately 300 kHz. A short-pass dichroic mirror (cutoff wavelength of 1180 nm) splits the comb spectrum into two arms. The short-wavelength part is overlapped with the 1064 nm radiation and sent towards a diffraction gratings mounted in Littrow configuration. The diffracted comb is filtered out by an aperture and an interferometric filter that transmits the 1064 nm laser and a small part of the comb spectrum with wavelength around 1064 nm. The beat note is detected by two InGaAs photodiodes in a differential scheme (OSI Optoelectronics, FCI-InGaAs-75). A similar optical path is used to obtain the beat note between the signal laser and the long-wavelength portion of the comb spectrum. Both beat notes are detected with a minimum signal-to-noise ratio of 25 dB on a 100 kHz bandwidth.

The Nd:YAG is phase locked directly on the beat note with the comb with a bandwidth of about 700 Hz. To implement the indirect locking scheme, we first mix the pump–comb beat note with the carrier-envelop offset frequency f 0 to obtain \({\bar{f}}_{{\rm{b}}:{\rm{pump}}}\). Then, a 14-bit direct digital synthesizer (Analog Devices, Inc., UG-207) creates \(\frac{{N}_{{\rm{signal}}}}{{N}_{{\rm{pump}}}}{\bar{f}}_{{\rm{b}}:{\rm{pump}}}\) from \({\bar{f}}_{{\rm{b}}:{\rm{pump}}}\). Finally, we mix the signal–comb beat note with the offset frequency, obtaining \({f}_{{\rm{b}}:{\rm{signal}}}\), which is mixed with the rest yielding \({\bar{f}}_{{\rm{b}}:{\rm{signal}}}-\frac{{N}_{{\rm{signal}}}}{{N}_{{\rm{pump}}}}{\bar{f}}_{{\rm{b}}:{\rm{pump}}}\). This frequency is used as the error signal for the phase-lock loop that acts on the diode laser current with a bandwidth exceeding 200 kHz.

Experimental Setup

A mixture of 20% CO in Kr at a backing pressure of 2 bar expands through the nozzle of a pulsed solenoid valve (Parker Hannifin Corp., modified General Valve series 99), which is kept at 140 K and operates at 10 Hz. After a 1-mm skimmer, the collimated beam has a velocity of 318 m/s. A pulsed laser at 206 nm with a fluence of 1 mJ and a bandwidth of 120 MHz transfers the CO molecules from the ground state \({X}^{1}{{\rm{\Sigma }}}^{+}\) to the upper \({\rm{\Lambda }}\)-doubling component of the \({a}^{3}{\rm{\Pi }},\,v=\mathrm{0,}\,J=1\) state. Continuing their flight, the molecules interact twice with the QCL radiation that drives the vibrational transition to the \(v\mathrm{=1,}\,J=\mathrm{1,}\,-\) state: a corner cube retro-reflects the QCL. Three couples of coils in Helmholtz configuration compensate the stray magnetic field in the region where the QCL interacts with the molecules.

Finally, the molecules are detected by multiphoton resonance-enhanced ionization in a 1 + 1 process at 283 nm via the intermediate \({b}^{3}{{\rm{\Sigma }}}^{+},v^{\prime} =\mathrm{1,}\,N^{\prime} =\mathrm{1,}\,-\) state. This radiation is provided by a tunable pulsed dye laser (Radiant Dyes Laser & Accessories GmbH, NarrowScan) pumped with a frequency doubled Nd:YAG laser source with 10 Hz repetition rate (InnoLas Photonics GmbH, SpitLight 1200). We used Fluorescine 27 diluted in methanol to produce radiation at about 566 nm and then we double the frequency with a BBO crystal. A few mJ suffice to saturate the ionization process. Immediately before the CO molecules are ionized, we turn on a strong electric field to accelerate the ions toward a microchannel-plate detector. Such field allows the otherwise forbidden transition between states of the same parity.

The 206 nm and 5.8 μm beams are parallel, while the 283-nm beam is perpendicular to them. We use a micrometric translation stage to finely change the position of the ionization laser along the direction parallel to the mid IR laser.

Uncertainty on the spectroscopic measurements

A corner cube retro-reflects the QCL beam. The two anti-parallel laser beams induce Doppler shifts on the transition that are equal in magnitude but opposite in sign. Thus, when the molecular beam and the mid-IR laser beam are not perpendicular, we observe a symmetric splitting of the absorption line. We record the magnitude of the splitting in dependence on the angle between the laser beam and the molecular beam, and, finally, we settle at the position corresponding to the minimal splitting. The remaining systematic uncertainty is due to imperfect parallelity of the counter-propagating mid-IR beams. This has been measured and it is better than 10−4 rad, which corresponds to a final uncertainty on the transition frequency of 2.6 kHz.

We estimate the Stark and second-order Zeeman shifts due to stray fields to be lower than 10 Hz. Since we prepare and detect the molecules with focused ns lasers at precisely-known times and positions, we know the speed of the molecules, 318.5 ± 2 m/s. Thus, we calculate the second-order Doppler shift, +29.4 ± 0.4 Hz, and we subtract it from the measured frequency. The remaining systematic uncertainty is due to the Cs fountain standard accuracy33 and to fibre link phase slips23, both smaller than 100 mHz. Therefore, the total systematic uncertainty is estimated as 2.6 kHz.

The Zeeman shift of the \({\rm{\Delta }}M=\pm 1\) is of the order of 500 kHz/Gauss, whereas the \({\rm{\Delta }}M=0\) are shifted by about 10 kHz/Gauss. By canceling the Zeeman shift on the \({\rm{\Delta }}M=\pm 1\) transitions, we estimate that the residual Zeeman shift on the \({\rm{\Delta }}M=0\) transition is smaller than 1 kHz. We repeated the canceling procedure several times between the scans and we found no variation of the compensating magnetic field. This contributes to the statistical uncertainty, together with the uncertainty in the alignment of the beams, whose procedure is described above, and with the fluctuations in the population of metastable CO molecules. The distribution of the experimental measurements has a Gaussian shape with a standard deviation of 7.9 kHz. Our set of 22 scans yields a total statistical uncertainty of 1.7 kHz.